27.2.1 相似三角形的判定(第2课时)课件
文档属性
| 名称 | 27.2.1 相似三角形的判定(第2课时)课件 |  | |
| 格式 | zip | ||
| 文件大小 | 215.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-30 08:38:42 | ||
图片预览



文档简介
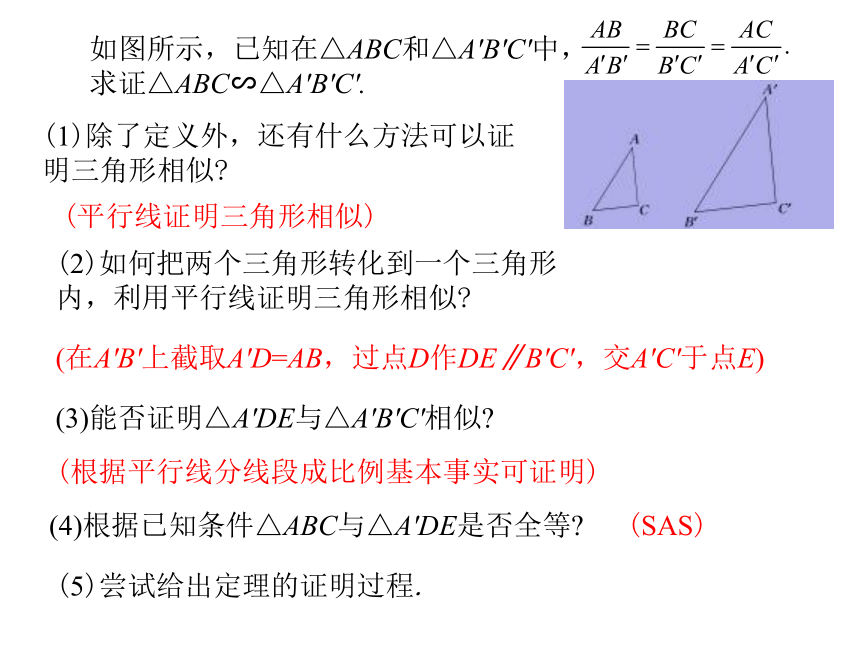
课件13张PPT。九年级数学·下 新课标[人]第二十七章 相 似27.2.1 相似三角形的判定(第2课时)27.2 相似三角形学 习 新 知问题思考(1)证明三角形相似的方法是什么?(三角形相似的定义、平行线证明三角形相似)(2)全等三角形如何定义的?证明全等三角形有几种方法?(对应角、对应边相等的三角形是全等三角形;SSS,SAS,ASA,AAS,HL)(3)全等三角形与相似三角形有什么关系?三边法证明三角形相似(1)同桌分别画边长为2 cm,3 cm,4 cm的三角形和边长为4 cm,6 cm,8 cm的三角形,然后猜想、判断两个三角形是否相似.(2)如果一个三角形的三边是另一个三角形三边的k倍,那么这两个三角形是否相似?(3)猜想:三角形三边对应成比例,两个三角形是否相似?你能证明这个结论吗?如图所示,已知在△ABC和△A'B'C'中,
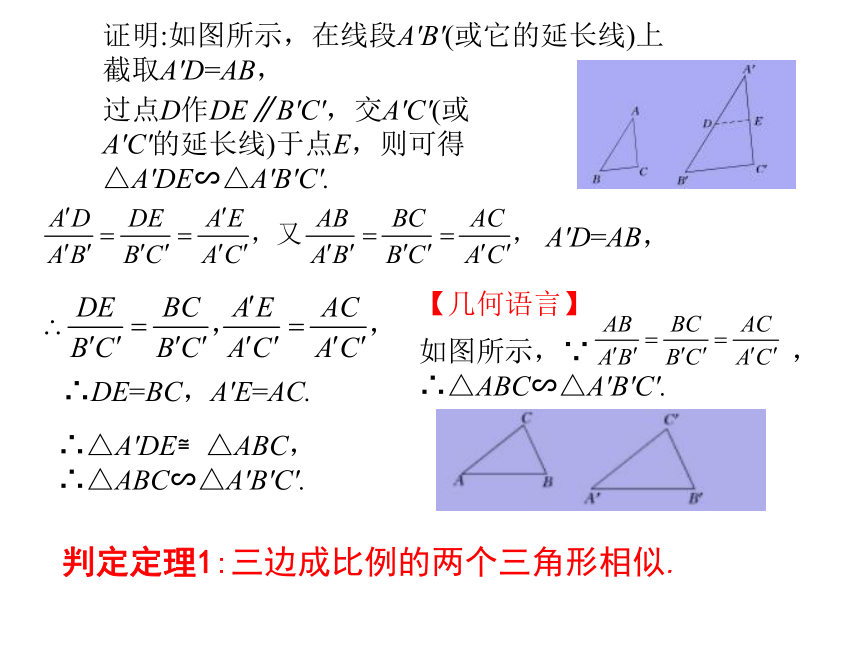
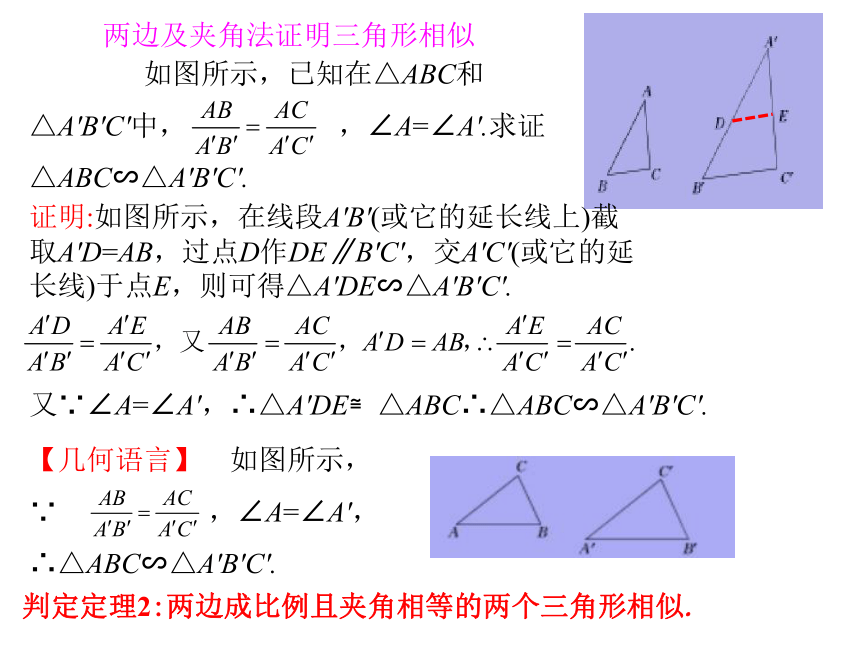
求证△ABC∽△A'B'C'.(1)除了定义外,还有什么方法可以证明三角形相似?(平行线证明三角形相似)(2)如何把两个三角形转化到一个三角形内,利用平行线证明三角形相似?(在A'B'上截取A'D=AB,过点D作DE∥B'C',交A'C'于点E)(3)能否证明△A'DE与△A'B'C'相似?(根据平行线分线段成比例基本事实可证明)(4)根据已知条件△ABC与△A'DE是否全等?(SAS)(5)尝试给出定理的证明过程.[知识拓展] (1)当已知条件中有三边时,可考虑用“三边成比例的两个三角形相似”证明三角形相似.(2)在应用相似三角形的判定定理1时,一定要注意先求两个三角形中大边与大边,中间边与中间边,小边与小边的比值,然后判断上述比值是否相等,从而判断两个三角形是否相似.(3)对于已知两组边的长度及边的夹角相等的情况,常用相似三角形的判定定理2判定两个三角形相似.(4)在应用相似三角形的判定定理2时,一定要注意必须是两边夹角相等才行.(5)在应用相似三角形的判定定理2时,还要注意一些隐含条件,如公共角、对顶角等.检测反馈1.若△ABC的各边都分别扩大为原来的2倍得到△A1B1C1,下列结论正确的是 ( )
A.△ABC与△A1B1C1的对应角不相等
B.△ABC与△A1B1C1不一定相似
C.△ABC与△A1B1C1的相似比为
D.△ABC与△A1B1C1的相似比为2解析:△ABC的各边都分别扩大为原来的2倍,则两个三角形的对应边成比例,且比值为 ,由三边对应成比例的两个三角形相似,可得△ABC∽△A1B1C1,且相似比为 .故选C.C2.如图所示,小正方形的边长均为1,则图中三角形(阴影部分)与△ABC相似的是( ) 解析:由题意得AB=2,BC= ,AC= ,A中三角形的三边长分别为1, , ,三边不对应成比例,A错误;B中三角形的三边长分别为1, , ,则有 ,故B正确;C中三角形的三边长分别为3, , ,三边不对应成比例,故C错误;D中三角形的三边长分别为2, , ,三边不对应成比例,故D错误.故选B.B3.下列条件中,能判定△ABC相似于△DEF的有( )
①∠A=45°,AB=12,AC=15,∠D=45°,DE=16,DF=40;②AB=12,BC=15,AC=24,DE=20,EF=25,DF=40;③∠A=47°,AB=15,AC=20,∠D=47°,DE=28,DF=21.
A.0个 B.1个 C.2个 D.3个所以△ABC与△DEF不相似;所以△ABC∽△DEF.所以△ABC与△DEF不相似.故选B.B4.如图所示,在△ABC中,D,E分别在AB,AC边上,且 BC=5,则DE= .?解析:∵ ,∠A=∠A ,∴△ABC∽△ADE, ∴ , ∵BC=5,∴DE= .故填 .5.根据下列条件,判断△ABC与△A'B'C'是否相似,并说明理由.
(1)∠A=40°,AB=8,AC=15,∠A'=40°,A'B'=16,A'C'=30;
(2)AB=10,BC=12,AC=15,A'B'=1.5,B'C'=1.8,A'C'=2.25.解:(1)∵AB=8,AC=15,A'B'=16,A'C'=30,
∴ ,
又∵∠A=∠A'=40°,∴△ABC∽△A'B'C'.
(2)∵AB=10,BC=12,AC=15,A'B'=1.5,B'C'=1.8,A'C'=2.25,
∴ ,∴△ABC∽△A'B'C'.
求证△ABC∽△A'B'C'.(1)除了定义外,还有什么方法可以证明三角形相似?(平行线证明三角形相似)(2)如何把两个三角形转化到一个三角形内,利用平行线证明三角形相似?(在A'B'上截取A'D=AB,过点D作DE∥B'C',交A'C'于点E)(3)能否证明△A'DE与△A'B'C'相似?(根据平行线分线段成比例基本事实可证明)(4)根据已知条件△ABC与△A'DE是否全等?(SAS)(5)尝试给出定理的证明过程.[知识拓展] (1)当已知条件中有三边时,可考虑用“三边成比例的两个三角形相似”证明三角形相似.(2)在应用相似三角形的判定定理1时,一定要注意先求两个三角形中大边与大边,中间边与中间边,小边与小边的比值,然后判断上述比值是否相等,从而判断两个三角形是否相似.(3)对于已知两组边的长度及边的夹角相等的情况,常用相似三角形的判定定理2判定两个三角形相似.(4)在应用相似三角形的判定定理2时,一定要注意必须是两边夹角相等才行.(5)在应用相似三角形的判定定理2时,还要注意一些隐含条件,如公共角、对顶角等.检测反馈1.若△ABC的各边都分别扩大为原来的2倍得到△A1B1C1,下列结论正确的是 ( )
A.△ABC与△A1B1C1的对应角不相等
B.△ABC与△A1B1C1不一定相似
C.△ABC与△A1B1C1的相似比为
D.△ABC与△A1B1C1的相似比为2解析:△ABC的各边都分别扩大为原来的2倍,则两个三角形的对应边成比例,且比值为 ,由三边对应成比例的两个三角形相似,可得△ABC∽△A1B1C1,且相似比为 .故选C.C2.如图所示,小正方形的边长均为1,则图中三角形(阴影部分)与△ABC相似的是( ) 解析:由题意得AB=2,BC= ,AC= ,A中三角形的三边长分别为1, , ,三边不对应成比例,A错误;B中三角形的三边长分别为1, , ,则有 ,故B正确;C中三角形的三边长分别为3, , ,三边不对应成比例,故C错误;D中三角形的三边长分别为2, , ,三边不对应成比例,故D错误.故选B.B3.下列条件中,能判定△ABC相似于△DEF的有( )
①∠A=45°,AB=12,AC=15,∠D=45°,DE=16,DF=40;②AB=12,BC=15,AC=24,DE=20,EF=25,DF=40;③∠A=47°,AB=15,AC=20,∠D=47°,DE=28,DF=21.
A.0个 B.1个 C.2个 D.3个所以△ABC与△DEF不相似;所以△ABC∽△DEF.所以△ABC与△DEF不相似.故选B.B4.如图所示,在△ABC中,D,E分别在AB,AC边上,且 BC=5,则DE= .?解析:∵ ,∠A=∠A ,∴△ABC∽△ADE, ∴ , ∵BC=5,∴DE= .故填 .5.根据下列条件,判断△ABC与△A'B'C'是否相似,并说明理由.
(1)∠A=40°,AB=8,AC=15,∠A'=40°,A'B'=16,A'C'=30;
(2)AB=10,BC=12,AC=15,A'B'=1.5,B'C'=1.8,A'C'=2.25.解:(1)∵AB=8,AC=15,A'B'=16,A'C'=30,
∴ ,
又∵∠A=∠A'=40°,∴△ABC∽△A'B'C'.
(2)∵AB=10,BC=12,AC=15,A'B'=1.5,B'C'=1.8,A'C'=2.25,
∴ ,∴△ABC∽△A'B'C'.
