27.2.1 相似三角形的判定(第3课时)课件
文档属性
| 名称 | 27.2.1 相似三角形的判定(第3课时)课件 |  | |
| 格式 | zip | ||
| 文件大小 | 199.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-29 20:29:17 | ||
图片预览



文档简介
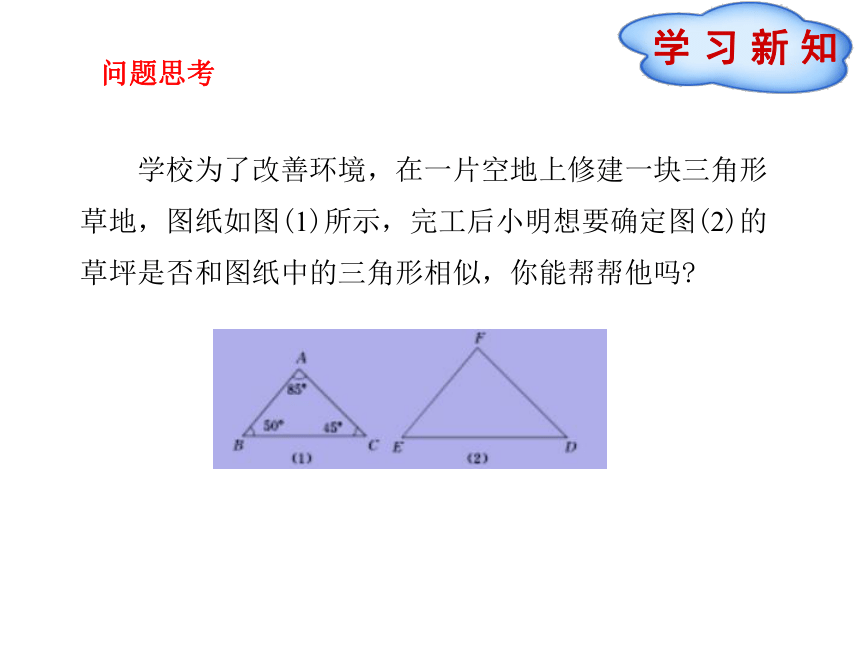
课件12张PPT。九年级数学·下 新课标[人]第二十七章 相 似27.2.1 相似三角形的判定(第3课时)27.2 相似三角形学 习 新 知 学校为了改善环境,在一片空地上修建一块三角形草地,图纸如图(1)所示,完工后小明想要确定图(2)的草坪是否和图纸中的三角形相似,你能帮帮他吗? 问题思考两角分别相等的两个三角形相似【动手操作】
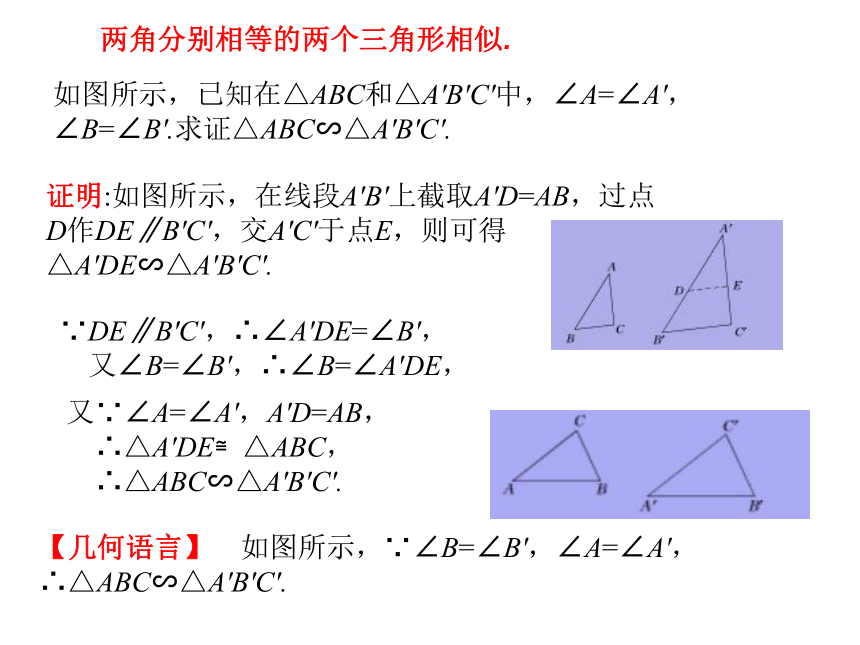
(1)同桌两个人分别画出△ABC,其中∠A=37°,∠B=65°.(2)分别测量AB,BC的长度(或测量AC,AB的长度),判断两个三角形是否相似. (3)根据操作、测量,猜想判定三角形相似的方法.(4)能证明你的猜想吗?写出已知、求证和证明过程.(5)用文字语言叙述你的结论,并用几何语言表示.两角分别相等的两个三角形相似.如图所示,已知在△ABC和△A'B'C'中,∠A=∠A',∠B=∠B'.求证△ABC∽△A'B'C'.
证明:如图所示,在线段A'B'上截取A'D=AB,过点D作DE∥B'C',交A'C'于点E,则可得△A'DE∽△A'B'C'.∵DE∥B'C',∴∠A'DE=∠B',
又∠B=∠B',∴∠B=∠A'DE,又∵∠A=∠A',A'D=AB,
∴△A'DE≌△ABC,
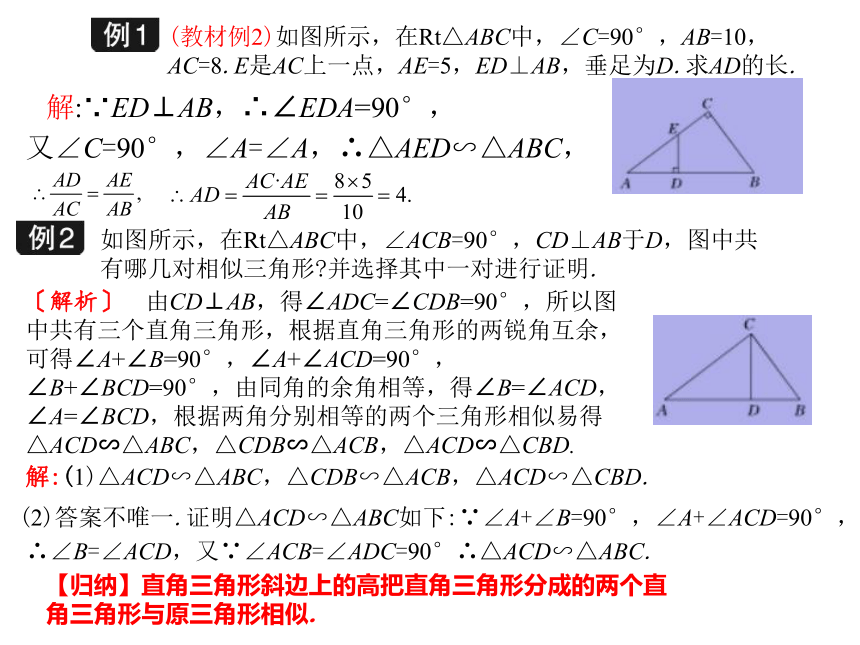
∴△ABC∽△A'B'C'.【几何语言】 如图所示,∵∠B=∠B',∠A=∠A',∴△ABC∽△A'B'C'.一条直角边和斜边对应成比例的两个三角形相似(1)证明直角三角形全等的方法有哪些?(SSS,SAS,ASA,AAS,HL)(2)证明直角三角形相似可以用哪些方法?(三边成比例、两边成比例且夹角相等、两角分别相等的两个三角形相似)(3)类比直角三角形全等的判定方法,如果一条直角边和斜边分别成比例,两个直角三角形相似吗? 一条直角边和斜边对应成比例的两个直角三角形相似.如图所示,在Rt△ABC和Rt△A'B'C'中,∠C=90°,∠C'=90°, .求证Rt△ABC∽Rt△A'B'C'.由于三边成比例的两个三角形相似,而已知条件中有两边对应成比例,所以只需证明另一对直角边也成比例即可.在直角三角形中三边之间的关系满足勾股定理,所以可设 ,用勾股定理分别求出BC,B'C'的值,求得 ,从而得证.证明:设 ,则AB=kA'B',AC=kA'C'.∴Rt△ABC∽Rt△A'B'C'.(教材例2)如图所示,在Rt△ABC中,∠C=90°,AB=10,AC=8.E是AC上一点,AE=5,ED⊥AB,垂足为D.求AD的长.解:∵ED⊥AB,∴∠EDA=90°,又∠C=90°,∠A=∠A,∴△AED∽△ABC,如图所示,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,图中共有哪几对相似三角形?并选择其中一对进行证明.〔解析〕 由CD⊥AB,得∠ADC=∠CDB=90°,所以图中共有三个直角三角形,根据直角三角形的两锐角互余,可得∠A+∠B=90°,∠A+∠ACD=90°,∠B+∠BCD=90°,由同角的余角相等,得∠B=∠ACD,∠A=∠BCD,根据两角分别相等的两个三角形相似易得△ACD∽△ABC,△CDB∽△ACB,△ACD∽△CBD.解:(1)△ACD∽△ABC,△CDB∽△ACB,△ACD∽△CBD.(2)答案不唯一.证明△ACD∽△ABC如下:∵∠A+∠B=90°,∠A+∠ACD=90°,∴∠B=∠ACD,又∵∠ACB=∠ADC=90°∴△ACD∽△ABC.【归纳】直角三角形斜边上的高把直角三角形分成的两个直角三角形与原三角形相似.[知识拓展] (1)在有一组对应角相等的情况下,可以从两个方面选择突破口:寻找另一组对应角相等;寻找两个三角形中夹这个已知角的两条边的比相等.(2)直角三角形斜边上的高把直角三角形分成的两个直角三角形与原三角形相似.(3)若两个直角三角形满足一个锐角相等或两组直角边成比例或斜边和一条直角边成比例,则这两个直角三角形相似.1.相似三角形的判定定理3:两角分别相等的两个三角形相似.
2.直角三角形相似的判定方法:一条直角边和斜边对应成比例的两个直角三角形相似.一个锐角相等或两边对应成比例的两个直角三角形相似. 课堂小结检测反馈1.如图所示,已知∠C=∠E,则不一定能使△ABC∽△ADE的条件是 ( )
A.∠BAD=∠CAE B.∠B=∠D
C. D. 解析:由题意得∠C=∠E,若添加∠BAD=∠CAE,则可得∠BAC=∠DAE,利用两角法可判定△ABC∽△ADE,故A错误;若添加∠B=∠D,利用两角法可判定△ABC∽△ADE,故B错误;若添加 ,利用两边及夹角法可判定△ABC∽△ADE,故C错误;若添加 ,不能判定△ABC∽△ADE.故选D.D2.如图所示,∠ADE=∠ACD=∠ABC,图中相似三角形共有 ( )
A.1对 B.2对 C.3对 D.4对解析:∵∠ADE=∠ACD=∠ABC,∴DE∥BC,∴△ADE∽△ABC,∵DE∥BC,∴∠EDC=∠DCB,∵∠ACD=∠ABC,∴△EDC∽△DCB,同理∠ACD=∠ABC,∠A=∠A,∴△ABC∽△ACD,∵△ADE∽△ABC,△ABC∽△ACD,∴△ADE∽△ACD,∴共有4对.故选D.D3.如图所示,在△ABC中,D是AB边上一点,连接CD.请你添加一个适当的条件,使△ADC∽△ACB,那么添加的条件是 .?解析:在△ABC和△ACD中,∠DAC=∠CAB,若要△ADC∽△ACB,需添加的条件为:①∠ADC=∠ACB;②∠ACD=∠B;③ 或AC2=AB·AD.故填AC2=AD·AB或∠ACD=∠ABC或∠ADC=∠ACB.AC2=AD·AB或∠ACD=∠ABC或∠ADC=∠ACB.4.在△ABC中,∠ACB=90°,CD⊥AB于D, ,求△ACD与△CBD的相似比.解:如图所示,在Rt△ACB中,CD⊥AB,则△ACD∽△CBD,即CD2=AD·BD,令AD=2x,BD=3x(x>0),
∴CD2=6x2,∴CD= ∴△ACD与△CBD的相似比为5.如图所示,等边三角形ABC的边长为3,点P为BC上一点,且BP=1,点D为AC边上一点,若∠APD=60°,求CD的长.解:∵△ABC为等边三角形,
∴∠ABC=∠PCD=60°,
∴∠APC=∠ABP+∠BAP=60°+∠BAP,
又∠APC=∠APD+∠CPD=60°+∠CPD,
∴∠BAP=∠CPD.
又∵∠ABP=∠PCD=60°,
∴△ABP∽△PCD.
(1)同桌两个人分别画出△ABC,其中∠A=37°,∠B=65°.(2)分别测量AB,BC的长度(或测量AC,AB的长度),判断两个三角形是否相似. (3)根据操作、测量,猜想判定三角形相似的方法.(4)能证明你的猜想吗?写出已知、求证和证明过程.(5)用文字语言叙述你的结论,并用几何语言表示.两角分别相等的两个三角形相似.如图所示,已知在△ABC和△A'B'C'中,∠A=∠A',∠B=∠B'.求证△ABC∽△A'B'C'.
证明:如图所示,在线段A'B'上截取A'D=AB,过点D作DE∥B'C',交A'C'于点E,则可得△A'DE∽△A'B'C'.∵DE∥B'C',∴∠A'DE=∠B',
又∠B=∠B',∴∠B=∠A'DE,又∵∠A=∠A',A'D=AB,
∴△A'DE≌△ABC,
∴△ABC∽△A'B'C'.【几何语言】 如图所示,∵∠B=∠B',∠A=∠A',∴△ABC∽△A'B'C'.一条直角边和斜边对应成比例的两个三角形相似(1)证明直角三角形全等的方法有哪些?(SSS,SAS,ASA,AAS,HL)(2)证明直角三角形相似可以用哪些方法?(三边成比例、两边成比例且夹角相等、两角分别相等的两个三角形相似)(3)类比直角三角形全等的判定方法,如果一条直角边和斜边分别成比例,两个直角三角形相似吗? 一条直角边和斜边对应成比例的两个直角三角形相似.如图所示,在Rt△ABC和Rt△A'B'C'中,∠C=90°,∠C'=90°, .求证Rt△ABC∽Rt△A'B'C'.由于三边成比例的两个三角形相似,而已知条件中有两边对应成比例,所以只需证明另一对直角边也成比例即可.在直角三角形中三边之间的关系满足勾股定理,所以可设 ,用勾股定理分别求出BC,B'C'的值,求得 ,从而得证.证明:设 ,则AB=kA'B',AC=kA'C'.∴Rt△ABC∽Rt△A'B'C'.(教材例2)如图所示,在Rt△ABC中,∠C=90°,AB=10,AC=8.E是AC上一点,AE=5,ED⊥AB,垂足为D.求AD的长.解:∵ED⊥AB,∴∠EDA=90°,又∠C=90°,∠A=∠A,∴△AED∽△ABC,如图所示,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,图中共有哪几对相似三角形?并选择其中一对进行证明.〔解析〕 由CD⊥AB,得∠ADC=∠CDB=90°,所以图中共有三个直角三角形,根据直角三角形的两锐角互余,可得∠A+∠B=90°,∠A+∠ACD=90°,∠B+∠BCD=90°,由同角的余角相等,得∠B=∠ACD,∠A=∠BCD,根据两角分别相等的两个三角形相似易得△ACD∽△ABC,△CDB∽△ACB,△ACD∽△CBD.解:(1)△ACD∽△ABC,△CDB∽△ACB,△ACD∽△CBD.(2)答案不唯一.证明△ACD∽△ABC如下:∵∠A+∠B=90°,∠A+∠ACD=90°,∴∠B=∠ACD,又∵∠ACB=∠ADC=90°∴△ACD∽△ABC.【归纳】直角三角形斜边上的高把直角三角形分成的两个直角三角形与原三角形相似.[知识拓展] (1)在有一组对应角相等的情况下,可以从两个方面选择突破口:寻找另一组对应角相等;寻找两个三角形中夹这个已知角的两条边的比相等.(2)直角三角形斜边上的高把直角三角形分成的两个直角三角形与原三角形相似.(3)若两个直角三角形满足一个锐角相等或两组直角边成比例或斜边和一条直角边成比例,则这两个直角三角形相似.1.相似三角形的判定定理3:两角分别相等的两个三角形相似.
2.直角三角形相似的判定方法:一条直角边和斜边对应成比例的两个直角三角形相似.一个锐角相等或两边对应成比例的两个直角三角形相似. 课堂小结检测反馈1.如图所示,已知∠C=∠E,则不一定能使△ABC∽△ADE的条件是 ( )
A.∠BAD=∠CAE B.∠B=∠D
C. D. 解析:由题意得∠C=∠E,若添加∠BAD=∠CAE,则可得∠BAC=∠DAE,利用两角法可判定△ABC∽△ADE,故A错误;若添加∠B=∠D,利用两角法可判定△ABC∽△ADE,故B错误;若添加 ,利用两边及夹角法可判定△ABC∽△ADE,故C错误;若添加 ,不能判定△ABC∽△ADE.故选D.D2.如图所示,∠ADE=∠ACD=∠ABC,图中相似三角形共有 ( )
A.1对 B.2对 C.3对 D.4对解析:∵∠ADE=∠ACD=∠ABC,∴DE∥BC,∴△ADE∽△ABC,∵DE∥BC,∴∠EDC=∠DCB,∵∠ACD=∠ABC,∴△EDC∽△DCB,同理∠ACD=∠ABC,∠A=∠A,∴△ABC∽△ACD,∵△ADE∽△ABC,△ABC∽△ACD,∴△ADE∽△ACD,∴共有4对.故选D.D3.如图所示,在△ABC中,D是AB边上一点,连接CD.请你添加一个适当的条件,使△ADC∽△ACB,那么添加的条件是 .?解析:在△ABC和△ACD中,∠DAC=∠CAB,若要△ADC∽△ACB,需添加的条件为:①∠ADC=∠ACB;②∠ACD=∠B;③ 或AC2=AB·AD.故填AC2=AD·AB或∠ACD=∠ABC或∠ADC=∠ACB.AC2=AD·AB或∠ACD=∠ABC或∠ADC=∠ACB.4.在△ABC中,∠ACB=90°,CD⊥AB于D, ,求△ACD与△CBD的相似比.解:如图所示,在Rt△ACB中,CD⊥AB,则△ACD∽△CBD,即CD2=AD·BD,令AD=2x,BD=3x(x>0),
∴CD2=6x2,∴CD= ∴△ACD与△CBD的相似比为5.如图所示,等边三角形ABC的边长为3,点P为BC上一点,且BP=1,点D为AC边上一点,若∠APD=60°,求CD的长.解:∵△ABC为等边三角形,
∴∠ABC=∠PCD=60°,
∴∠APC=∠ABP+∠BAP=60°+∠BAP,
又∠APC=∠APD+∠CPD=60°+∠CPD,
∴∠BAP=∠CPD.
又∵∠ABP=∠PCD=60°,
∴△ABP∽△PCD.
