27.2.1 相似三角形的判定(第1课时)
文档属性
| 名称 | 27.2.1 相似三角形的判定(第1课时) |

|
|
| 格式 | zip | ||
| 文件大小 | 253.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-29 00:00:00 | ||
图片预览




文档简介
课件17张PPT。九年级数学·下 新课标[人] 第二十七章 相 似27.2.1 相似三角形的判定(第1课时)27.2 相似三角形学 习 新 知问题思考你知道金字塔有多高吗?传说法老命令祭师们测量金字塔的高度,祭师们为此伤透了脑筋,为了帮助祭师们解决困难,古希腊一位伟大的数学家泰勒斯利用巧妙的办法测量金字塔的高度(在金字塔旁边竖立一根木桩,当木桩影子的长度和木桩的长度相等时,只要测量金字塔的影子的长度,便可得出金字塔的高度),展示了他非凡的数学及科学才能.如图所示.认识相似三角形思考并回答:
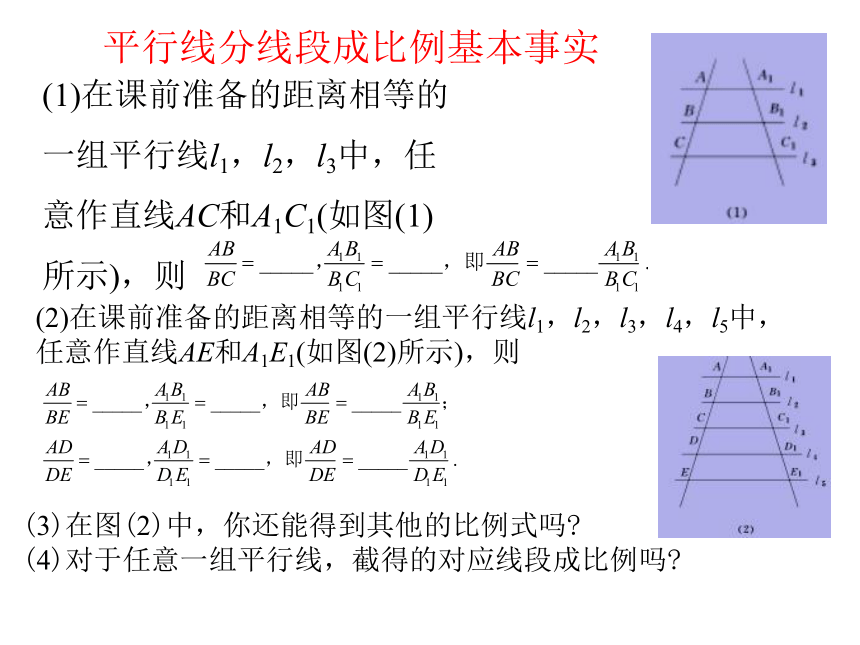
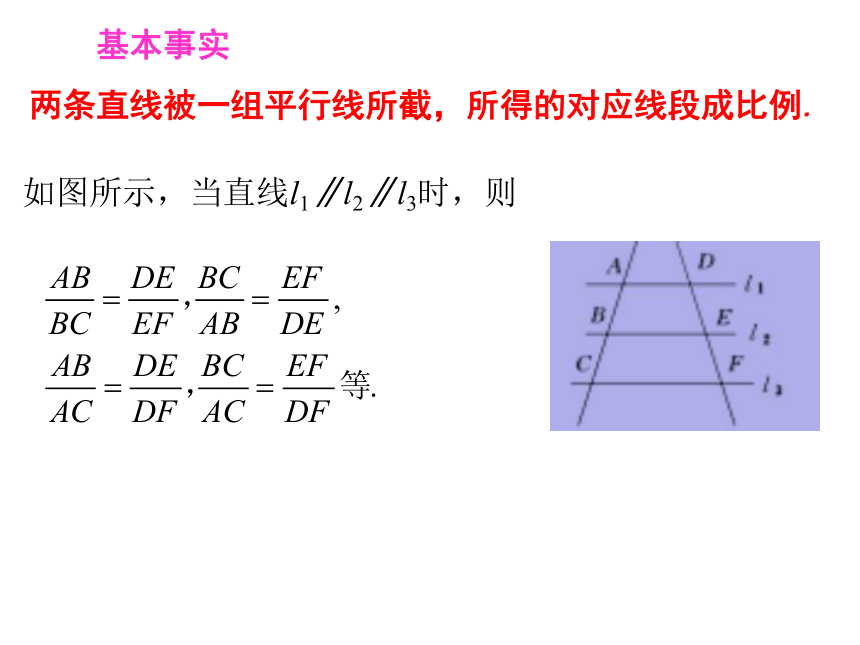
(1)类比相似多边形的概念,你能说出相似三角形的概念吗?(2)如果相似比是1,那么这两个三角形是什么关系?(3)△ABC与△A'B'C'的相似比为k,那么△A'B'C'与△ABC的相似比是多少?(4)类比相似多边形的性质,说出相似三角形的性质,并用几何语言表示.两条直线被一组平行线所截,所得的对应线段成比例.基本事实如图所示,当直线l1∥l2∥l3时,则平行线分线段成比例转化到三角形中活动1
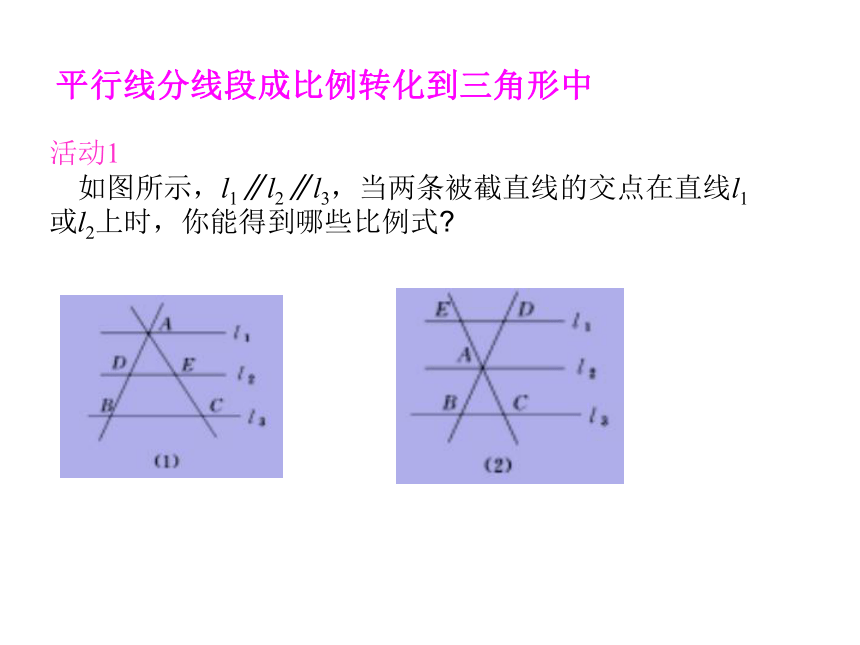
如图所示,l1∥l2∥l3,当两条被截直线的交点在直线l1或l2上时,你能得到哪些比例式? (1)相似三角形与全等三角形的联系与区别:全等三角形的大小相等,形状相同,而相似三角形的形状相同,大小不一定相等,所以全等三角形是相似三角形的特例,相似比是1∶1的两个相似三角形是全等三角形.[知识拓展](2)相似三角形的传递性:如果△ABC∽△A'B'C',△A'B'C'∽△A″B″C″,那么△ABC∽△A″B″C″.(3)在应用平行线分线段成比例这个基本事实时,找准被平行线截得的对应线段,被截线段不一定平行,当“上比下”的值为1时,说明这些平行线间的距离相等.(4)符合平行线证明三角形相似的图形有两个,我们称为“A”型和“X”型,如图所示,若DE∥BC,则△ADE∽△ABC.4.平行线证明三角形相似:“A”型和“X”型.平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.1.相似三角形的概念、表示:三个角分别相等,三条边成比例,△ABC∽△A'B'C'.课堂小结2.平行线分线段成比例的基本事实:两条直线被一组平行线所截,所得的对应线段成比例.3.平行线分线段成比例在三角形中的应用:平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.检测反馈1.(2015·乐山中考)如图所示,l1∥l2∥l3,两条直线与这三条平行线分别交于点A,B,C和D,E,F,已知 ,则 的值为 ( )A. B. C. D.解析:由平行线分线段成比例可得故选D.D2.如图所示,DE∥BC, , 则△ADE和△ABC的相似比为 ( )
A.1∶2 B.1∶3
C.2∶1 D.2∶3解析:∵DE∥BC,∴△ADE∽△ABC,∴△ADE和△ABC的相似比为 ,∵ ∴ .故填B.B? 解析:根据相似比的概念,可得△ABC与△DEF的相似比与△DEF与△ABC的相似比互为倒数,所以△DEF与△ABC的相似比是3∶5.故填3∶5.3.若△ABC与△DEF的相似比是5∶3,则△DEF与△ABC的相似比是 .3∶54.如图所示,在△ABC中,DE∥BC,若 ,DE=2,则BC的长为 .?解析:∵DE∥BC,∴△ADE∽△ABC,∴ ,又DE=2,∴ ,∴BC=6.故填6.65.如图所示,若DE∥BC,DE=3 cm,BC=5 cm,
求 的值.解:∵DE∥BC,∴△ADE∽△ABC,∵DE=3 cm,BC=5 cm,
(1)类比相似多边形的概念,你能说出相似三角形的概念吗?(2)如果相似比是1,那么这两个三角形是什么关系?(3)△ABC与△A'B'C'的相似比为k,那么△A'B'C'与△ABC的相似比是多少?(4)类比相似多边形的性质,说出相似三角形的性质,并用几何语言表示.两条直线被一组平行线所截,所得的对应线段成比例.基本事实如图所示,当直线l1∥l2∥l3时,则平行线分线段成比例转化到三角形中活动1
如图所示,l1∥l2∥l3,当两条被截直线的交点在直线l1或l2上时,你能得到哪些比例式? (1)相似三角形与全等三角形的联系与区别:全等三角形的大小相等,形状相同,而相似三角形的形状相同,大小不一定相等,所以全等三角形是相似三角形的特例,相似比是1∶1的两个相似三角形是全等三角形.[知识拓展](2)相似三角形的传递性:如果△ABC∽△A'B'C',△A'B'C'∽△A″B″C″,那么△ABC∽△A″B″C″.(3)在应用平行线分线段成比例这个基本事实时,找准被平行线截得的对应线段,被截线段不一定平行,当“上比下”的值为1时,说明这些平行线间的距离相等.(4)符合平行线证明三角形相似的图形有两个,我们称为“A”型和“X”型,如图所示,若DE∥BC,则△ADE∽△ABC.4.平行线证明三角形相似:“A”型和“X”型.平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.1.相似三角形的概念、表示:三个角分别相等,三条边成比例,△ABC∽△A'B'C'.课堂小结2.平行线分线段成比例的基本事实:两条直线被一组平行线所截,所得的对应线段成比例.3.平行线分线段成比例在三角形中的应用:平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.检测反馈1.(2015·乐山中考)如图所示,l1∥l2∥l3,两条直线与这三条平行线分别交于点A,B,C和D,E,F,已知 ,则 的值为 ( )A. B. C. D.解析:由平行线分线段成比例可得故选D.D2.如图所示,DE∥BC, , 则△ADE和△ABC的相似比为 ( )
A.1∶2 B.1∶3
C.2∶1 D.2∶3解析:∵DE∥BC,∴△ADE∽△ABC,∴△ADE和△ABC的相似比为 ,∵ ∴ .故填B.B? 解析:根据相似比的概念,可得△ABC与△DEF的相似比与△DEF与△ABC的相似比互为倒数,所以△DEF与△ABC的相似比是3∶5.故填3∶5.3.若△ABC与△DEF的相似比是5∶3,则△DEF与△ABC的相似比是 .3∶54.如图所示,在△ABC中,DE∥BC,若 ,DE=2,则BC的长为 .?解析:∵DE∥BC,∴△ADE∽△ABC,∴ ,又DE=2,∴ ,∴BC=6.故填6.65.如图所示,若DE∥BC,DE=3 cm,BC=5 cm,
求 的值.解:∵DE∥BC,∴△ADE∽△ABC,∵DE=3 cm,BC=5 cm,
