27.2.3 相似三角形应用举例(第2课时)
文档属性
| 名称 | 27.2.3 相似三角形应用举例(第2课时) |  | |
| 格式 | zip | ||
| 文件大小 | 240.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-29 20:47:54 | ||
图片预览


文档简介
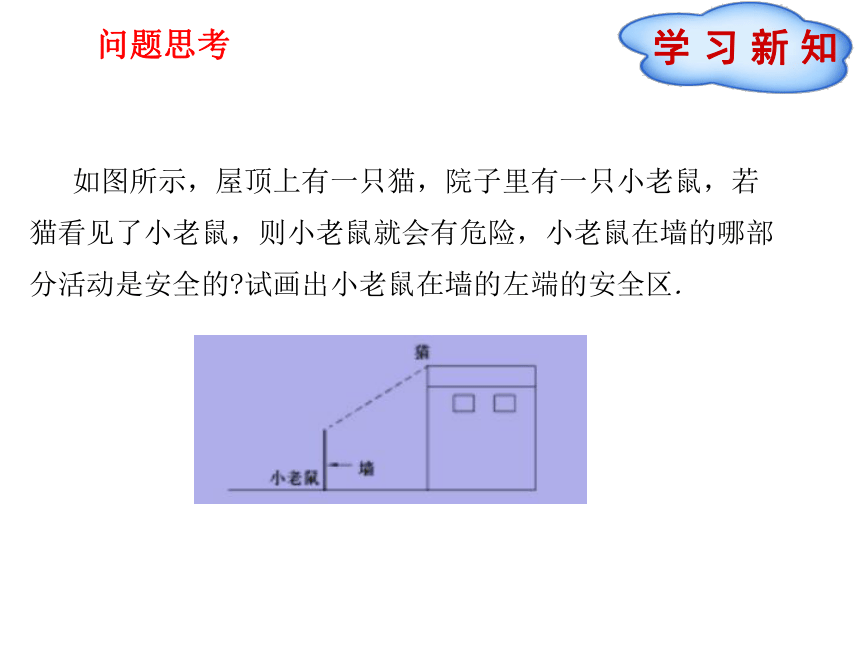
课件11张PPT。九年级数学·下 新课标[人]第二十七章 相似27.2.3 相似三角形应用举例(第2课时)学 习 新 知问题思考 如图所示,屋顶上有一只猫,院子里有一只小老鼠,若猫看见了小老鼠,则小老鼠就会有危险,小老鼠在墙的哪部分活动是安全的?试画出小老鼠在墙的左端的安全区.(教材例6)如图(1)所示,左、右并排的两棵大树的高分别为AB=8 m和CD=12 m,两树底部的距离BD=5 m,一个人估计自己眼睛距地面1.6 m. 她沿着正对这两棵树的一条水平直路l从左向右前进,当她与左边较低的树的距离小于多少时,就看不到右边较高的树的顶端C了?思考:(1)在图(1)中,这个人观察的盲区是哪部分?
(2)当她自左向右前进中,她的视线与两棵树的顶端恰好在同一条直线上时,如图(2)所示,她观察的盲区是哪部分?
(3)如果她再向右走,她还能看到右边较高的树的顶端吗?解:如图(2)所示,假设观察者从左向右走到点E时,她的眼睛的位置点E与两棵树的顶端A,C恰在一条直线上.∵AB⊥l,CD⊥l,
∴AB∥CD.
∴△AEH∽△CEK,解得EH=8(m).
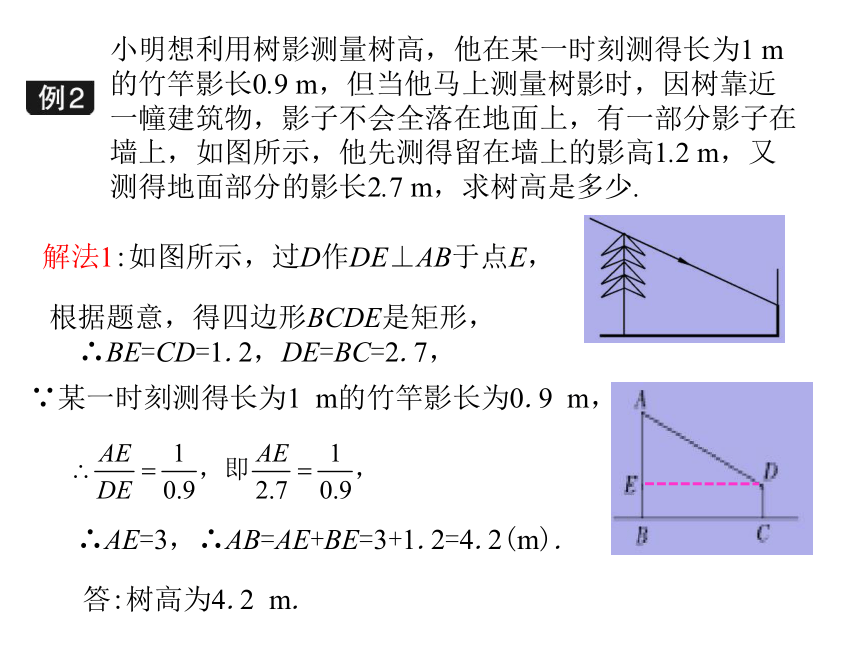
由此可知,如果观察者继续前进,当她与左边的树的距离小于8 m时,由于这棵树的遮挡,她看不到右边树的顶端C.小明想利用树影测量树高,他在某一时刻测得长为1 m的竹竿影长0.9 m,但当他马上测量树影时,因树靠近一幢建筑物,影子不会全落在地面上,有一部分影子在墙上,如图所示,他先测得留在墙上的影高1.2 m,又测得地面部分的影长2.7 m,求树高是多少.解法1:如图所示,过D作DE⊥AB于点E,根据题意,得四边形BCDE是矩形,
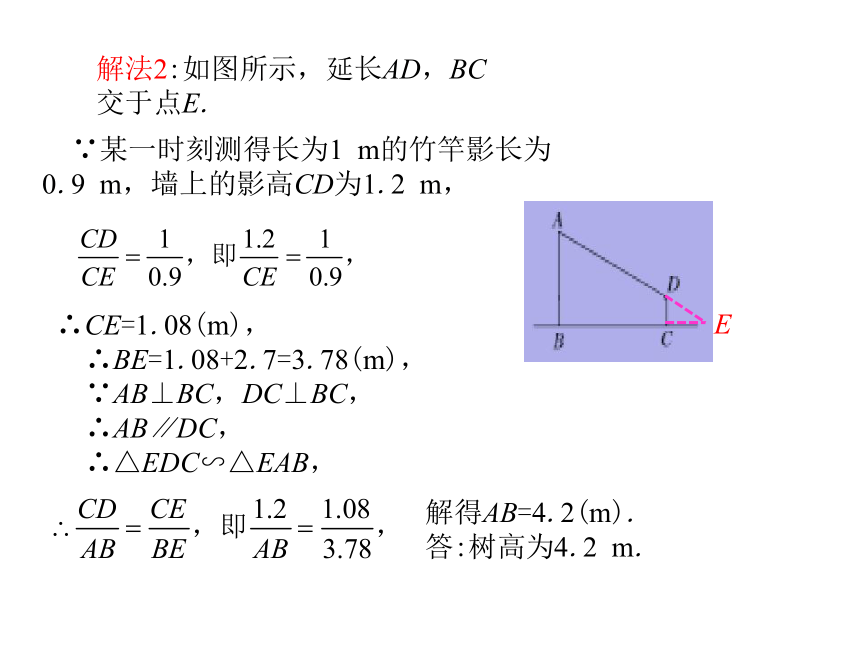
∴BE=CD=1.2,DE=BC=2.7,∵某一时刻测得长为1 m的竹竿影长为0.9 m,∴AE=3,∴AB=AE+BE=3+1.2=4.2(m).答:树高为4.2 m. ∵某一时刻测得长为1 m的竹竿影长为0.9 m,墙上的影高CD为1.2 m,解法2:如图所示,延长AD,BC交于点E.E∴CE=1.08(m),
∴BE=1.08+2.7=3.78(m),
∵AB⊥BC,DC⊥BC,
∴AB∥DC,
∴△EDC∽△EAB,解得AB=4.2(m).
答:树高为4.2 m.解法3:如图所示,过点C作CE∥AD交AB于点E,∵AE∥CD,EC∥AD,
∴四边形AECD是平行四边形,
∴AE=CD=1.2 m,又在平行投影中,同一时刻物高与影长成比例,即BE=2.7× =3(m).
∴AB=AE+EB=1.2+3=4.2(m).
答:树高为4.2 m.【归纳】
(1)求树高常用的方法:①根据相似三角形对应线段成比例,列方程求解即可;②在同一时刻,物体的实际高度和影长成比例,据此列方程即可求解.
(2)求树高常用的辅助线:①作垂直,构造相似三角形;②作平行,构造相似三角形;③延长两条直线相交,构造相似三角形.检测反馈1.如图所示,为估算某河的宽度,在河对岸选定一个目标点A,在近岸取点B,C,D,使得AB⊥BC,CD⊥BC,点E在BC上,并且点A,E,D在同一条直线上.若测得BE=20 m,EC=10 m,CD=20 m,则河的宽度AB等于 ( )
A.60 m B.40 m C.30 m D.20 m解析:∵AB⊥BC,CD⊥BC,∴△BAE∽△CDE,∴ .∵BE=20 m,CE=10 m,CD=20 m,∴ .解得AB=40.故选B.B2.如图(1)所示,为了测量某建筑物的高AB,在距离B点35 m的D处安置测角仪,测得A点的仰角α为45°,若仪器CD高为1.4 m,则高AB为 .?解析:如图(2)所示,过点C作CE⊥AB于点E.根据题意,在Rt△ACE中,CE=35 m,∠α=45°,∴AE=35 m.则AB的长为AE+BE=36.4 m.故填36.4 m.36.4 m3.如图所示,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条直角边DE=40 cm,EF=20 cm,测得边DF离地面的高度AC=1.5 m,CD=8 m,则树高AB= m.?解析:∵∠DEF=∠BCD=90°,∠D=∠D,∴△DEF∽△DCB,∴ ,∵DE=40 cm=0.4 m,EF=20 cm=0.2 m,AC=1.5 m,CD=8 m,∴ ,∴BC=4(m),∴AB=AC+BC=1.5+4=5.5(m).故填5.5.5.54.如图所示,九年级(1)班课外活动小组利用标杆测量学校旗杆的高度,已知标杆高度CD=3 m,标杆与旗杆的水平距离BD=15 m,人的眼睛与地面的高度EF=1.6 m,人与标杆CD的水平距离DF=2 m,求旗杆AB的高度.解:∵CD⊥FB,AB⊥FB,
∴CD∥AB,∴△CGE∽△AHE.∴AH=11.9.
∴AB=AH+HB=AH+EF=11.9+1.6=13.5(m).
答:旗杆AB的高度为13.5 m.
(2)当她自左向右前进中,她的视线与两棵树的顶端恰好在同一条直线上时,如图(2)所示,她观察的盲区是哪部分?
(3)如果她再向右走,她还能看到右边较高的树的顶端吗?解:如图(2)所示,假设观察者从左向右走到点E时,她的眼睛的位置点E与两棵树的顶端A,C恰在一条直线上.∵AB⊥l,CD⊥l,
∴AB∥CD.
∴△AEH∽△CEK,解得EH=8(m).
由此可知,如果观察者继续前进,当她与左边的树的距离小于8 m时,由于这棵树的遮挡,她看不到右边树的顶端C.小明想利用树影测量树高,他在某一时刻测得长为1 m的竹竿影长0.9 m,但当他马上测量树影时,因树靠近一幢建筑物,影子不会全落在地面上,有一部分影子在墙上,如图所示,他先测得留在墙上的影高1.2 m,又测得地面部分的影长2.7 m,求树高是多少.解法1:如图所示,过D作DE⊥AB于点E,根据题意,得四边形BCDE是矩形,
∴BE=CD=1.2,DE=BC=2.7,∵某一时刻测得长为1 m的竹竿影长为0.9 m,∴AE=3,∴AB=AE+BE=3+1.2=4.2(m).答:树高为4.2 m. ∵某一时刻测得长为1 m的竹竿影长为0.9 m,墙上的影高CD为1.2 m,解法2:如图所示,延长AD,BC交于点E.E∴CE=1.08(m),
∴BE=1.08+2.7=3.78(m),
∵AB⊥BC,DC⊥BC,
∴AB∥DC,
∴△EDC∽△EAB,解得AB=4.2(m).
答:树高为4.2 m.解法3:如图所示,过点C作CE∥AD交AB于点E,∵AE∥CD,EC∥AD,
∴四边形AECD是平行四边形,
∴AE=CD=1.2 m,又在平行投影中,同一时刻物高与影长成比例,即BE=2.7× =3(m).
∴AB=AE+EB=1.2+3=4.2(m).
答:树高为4.2 m.【归纳】
(1)求树高常用的方法:①根据相似三角形对应线段成比例,列方程求解即可;②在同一时刻,物体的实际高度和影长成比例,据此列方程即可求解.
(2)求树高常用的辅助线:①作垂直,构造相似三角形;②作平行,构造相似三角形;③延长两条直线相交,构造相似三角形.检测反馈1.如图所示,为估算某河的宽度,在河对岸选定一个目标点A,在近岸取点B,C,D,使得AB⊥BC,CD⊥BC,点E在BC上,并且点A,E,D在同一条直线上.若测得BE=20 m,EC=10 m,CD=20 m,则河的宽度AB等于 ( )
A.60 m B.40 m C.30 m D.20 m解析:∵AB⊥BC,CD⊥BC,∴△BAE∽△CDE,∴ .∵BE=20 m,CE=10 m,CD=20 m,∴ .解得AB=40.故选B.B2.如图(1)所示,为了测量某建筑物的高AB,在距离B点35 m的D处安置测角仪,测得A点的仰角α为45°,若仪器CD高为1.4 m,则高AB为 .?解析:如图(2)所示,过点C作CE⊥AB于点E.根据题意,在Rt△ACE中,CE=35 m,∠α=45°,∴AE=35 m.则AB的长为AE+BE=36.4 m.故填36.4 m.36.4 m3.如图所示,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条直角边DE=40 cm,EF=20 cm,测得边DF离地面的高度AC=1.5 m,CD=8 m,则树高AB= m.?解析:∵∠DEF=∠BCD=90°,∠D=∠D,∴△DEF∽△DCB,∴ ,∵DE=40 cm=0.4 m,EF=20 cm=0.2 m,AC=1.5 m,CD=8 m,∴ ,∴BC=4(m),∴AB=AC+BC=1.5+4=5.5(m).故填5.5.5.54.如图所示,九年级(1)班课外活动小组利用标杆测量学校旗杆的高度,已知标杆高度CD=3 m,标杆与旗杆的水平距离BD=15 m,人的眼睛与地面的高度EF=1.6 m,人与标杆CD的水平距离DF=2 m,求旗杆AB的高度.解:∵CD⊥FB,AB⊥FB,
∴CD∥AB,∴△CGE∽△AHE.∴AH=11.9.
∴AB=AH+HB=AH+EF=11.9+1.6=13.5(m).
答:旗杆AB的高度为13.5 m.
