27.3 位似(第2课时)课件
文档属性
| 名称 | 27.3 位似(第2课时)课件 |  | |
| 格式 | zip | ||
| 文件大小 | 197.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-30 08:56:39 | ||
图片预览



文档简介
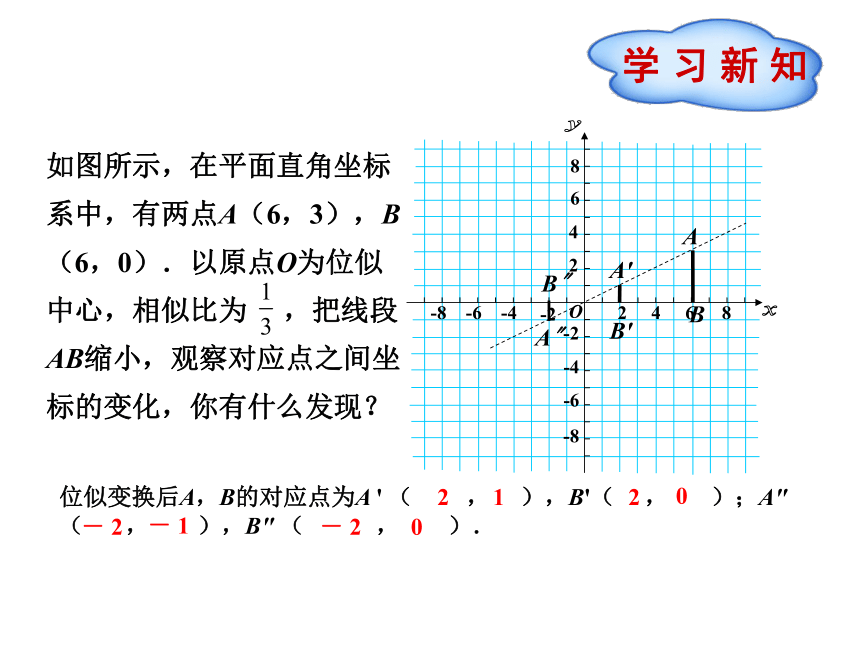
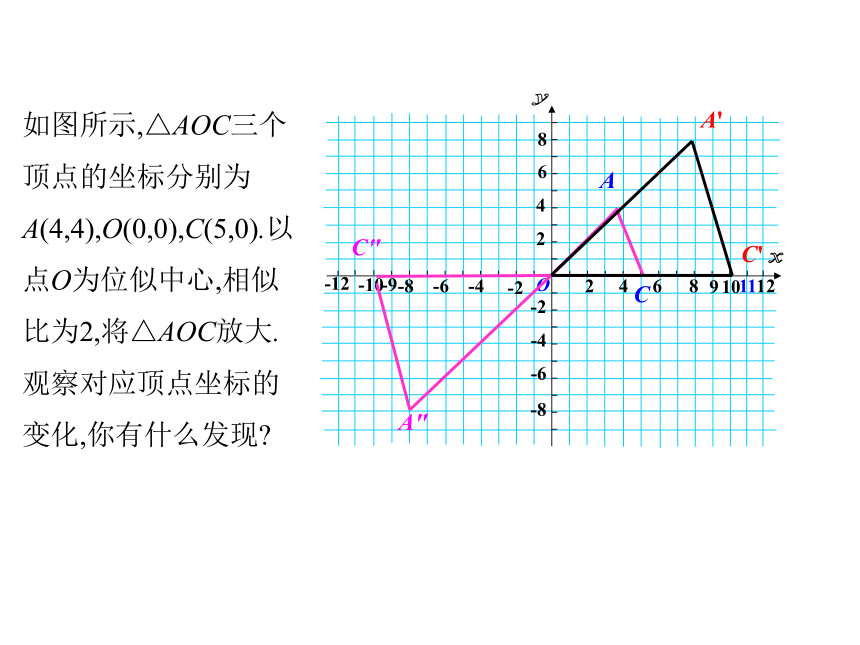
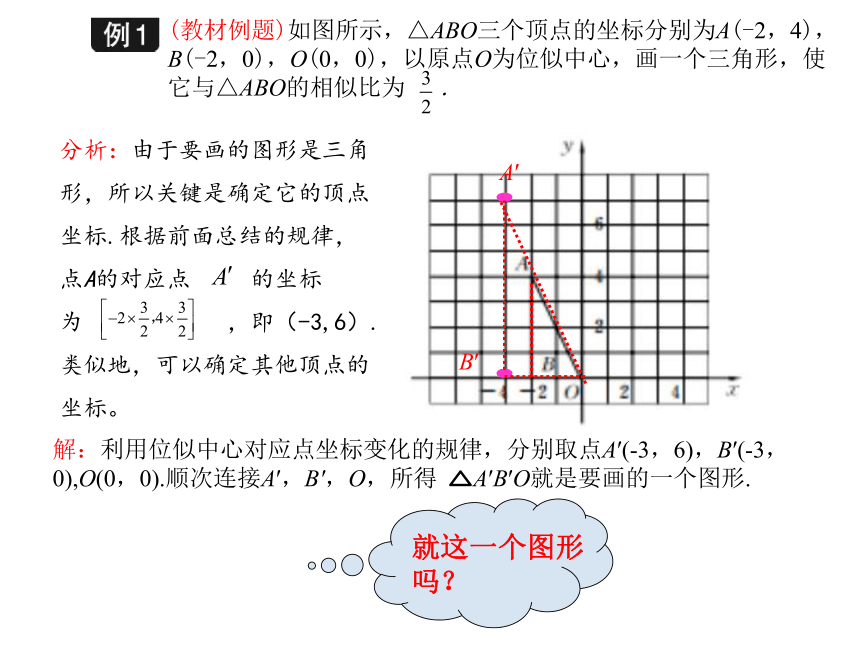
课件13张PPT。九年级数学·下 新课标[人]第二十七章 相 似 27.3 位似(第2课时)如图所示,在平面直角坐标系中,有两点A(6,3),B(6,0).以原点O为位似中心,相似比为 ,把线段AB缩小,观察对应点之间坐标的变化,你有什么发现?ABA'B'A〞B〞位似变换后A,B的对应点为A ' ( , ),B'( , );A"( , ),B" ( , ).2120- 2- 1- 20学 习 新 知ACA'C'A"C"如图所示,△AOC三个顶点的坐标分别为A(4,4),O(0,0),C(5,0).以点O为位似中心,相似比为2,将△AOC放大.观察对应顶点坐标的变化,你有什么发现?一般地,在平面直角坐标系中,如果以原点为位似中心,画出一个与原图形位似的图形,使它与原图形的相似比为k,那么与原图形上的点(x,y)对应的位似图形上的点的坐标为(kx,ky)或(-kx,-ky).总结(教材例题)如图所示,△ABO三个顶点的坐标分别为A(-2,4),B(-2,0),O(0,0),以原点O为位似中心,画一个三角形,使它与△ABO的相似比为 .分析:由于要画的图形是三角形,所以关键是确定它的顶点坐标.根据前面总结的规律,点A的对应点 的坐标为 ,即(-3,6).类似地,可以确定其他顶点的坐标。解:利用位似中心对应点坐标变化的规律,分别取点A′(-3,6),B′(-3,0),O(0,0).顺次连接A′,B′,O,所得 A′B′O就是要画的一个图形.A′B′如图所示,正方形OEFG和正方形ABCD是位似图形,点F的坐标为(-1,1),点C的坐标为(-4,2),求这两个正方形位似中心的坐标.【分析】(1)两个位似图形的特征是什么?(每对对应点与位似中心共线;对应线段平行或在同一条直线上)(2)位似中心的位置有几种?哪几种?(两种,位似中心在位似图形的同侧或异侧)(3)观察图形,当位似中心在位似图形同侧时,位似中心是不是在特殊直线上?(DG,AO在x轴上,故位似中心在x轴上)(4)当位似中心在位似图形同侧时,位似中心还在哪条与已知有关的直线上?(过对应点C,F所在的直线上或过对应点B,E所在的直线上) (求直线OC与直线DE的交点坐标,直线不唯一)(5)当位似中心在位似图形同侧时,如何求位似中心的坐标?(求直线CF(或BE)与x轴的交点坐标)(6)观察图形当位似中心在位似图形异侧时,位似中心在什么位置?(直线不唯一.直线OC,DE的交点)(7)当位似中心在位似图形异侧时,如何求位似中心的坐标?解:①当两个位似图形在位似中心同旁时,位似中心就是CF与x轴的交点,设直线CF的解析式为y=kx+b,将C(-4,2),F(-1,1)代入,得令y=0得x=2, ∴位似中心的坐标是(2,0).②当位似中心在两个正方形之间时,
可求直线OC的解析式为y=- x,直线DE的解析式为y= x+1,平移、旋转、轴对称、位似四种变换的异同我们已经学习了平移、轴对称、旋转和位似等图形的变化方式,你能在下图所示的图案中找到它们吗?四种变换有什么异同?【四种变换的异同】 图形经过平移、旋转、轴对称后,图形的位置虽然改变了,但是图形的大小和形状没有改变,即两个图形是全等的;而图形经过位似变换后,图形是相似的. (2)在直角坐标系中,把一个图形进行平移、轴对称、旋转和位似变换,其对应点的坐标都有各自的变化规律:①平移变换是横坐标或纵坐标加上(或减去)平移的距离;②轴对称变换,以x轴为对称轴,则对应点的横坐标相等,纵坐标互为相反数;以y轴为对称轴,则对应点的纵坐标相等,横坐标互为相反数.③在旋转变换中,一个图形绕原点旋转180°,则旋转前后两个图形上的对应点的横坐标与纵坐标分别互为相反数;④位似变换中,当以原点为位似中心时,变换前后两个图形上的对应点的横(或纵)坐标之比的绝对值等于相似比.[知识拓展] (1)以原点为位似中心的位似变换,其对应点的坐标关系可表示为(新图形与原图形的相似比为k):与P(x,y)位于位似中心同侧的对应点P1(kx,ky); 与P(x,y)位于位似中心异侧的对应点P2(-kx,-ky).当k>1时,是将图形扩大;当0 A.(-3,-3) B.(-3,-4)
C.(-4,-4) D.(-4,-3)解析:∵△ABC的三边分别扩大一倍得到△A1B1C1(顶点均在格点上),它们是以P点为位似中心的位似图形,根据位似图形的性质,对应点的连线相交于一点,连接BB1,CC1,交点即是P点,如图所示,∴P点的坐标为(-4,-3).故选D.D2.已知线段AB和CD,依据下列点的坐标,能判断AB和CD是以原点为位似中心的位似图形的是 ( )
A.A(2,3),B(-1,1),C(4,3),D(-2,1)
B.A(1,-5),B(-1,-2),C(1,-10),D(-1,-4)
C.A(-4,5),B(2,-2),C(4,5),D(-2,-2)
D.A(2,0),B(-1,0),C(-4,0),D(2,0)解析:根据以原点为位似图形的坐标特征,可得C,D点横、纵坐标为A,B点横、纵坐标的同一个倍数的只有D.故选D.D 3.如图所示,原点O是△ABC和△A1B1C1的位似中心,点A(1,0)与A1(-2,0)是对应点,△ABC的面积是 ,则△A1B1C1的面积是 .?解析:∵原点O是△ABC和△A1B1C1的位似中心,点A(1,0)与A1(-2,0)是对应点,∴△ABC和△A1B1C1的相似比为 ,由相似三角形的面积比等于相似比的平方,得△A1B1C1的面积是 ×4=6.故填6.64.如图所示的小方格都是边长为1的正方形,△ABC的顶点都在小正方形的顶点上,请完成以下问题.
(1)请在方格纸上建立平面直角坐标系,使A(2,3),C(6,2),则B点的坐标为 ;?
(2)以原点O为位似中心,在第一象限内将△ABC放大为原来的2倍,画出放大后的△A'B'C'.解:(1)∵A(2,3),C(6,2),
∴可得如图所示的平面直角坐标系.
∴点B的坐标为(2,1).(2)∵以原点O为位似中心,在第一象限内将△ABC放大为原来的2倍,∴A' (4,6),B' (4,2),C' (12,4),
如图所示.
可求直线OC的解析式为y=- x,直线DE的解析式为y= x+1,平移、旋转、轴对称、位似四种变换的异同我们已经学习了平移、轴对称、旋转和位似等图形的变化方式,你能在下图所示的图案中找到它们吗?四种变换有什么异同?【四种变换的异同】 图形经过平移、旋转、轴对称后,图形的位置虽然改变了,但是图形的大小和形状没有改变,即两个图形是全等的;而图形经过位似变换后,图形是相似的. (2)在直角坐标系中,把一个图形进行平移、轴对称、旋转和位似变换,其对应点的坐标都有各自的变化规律:①平移变换是横坐标或纵坐标加上(或减去)平移的距离;②轴对称变换,以x轴为对称轴,则对应点的横坐标相等,纵坐标互为相反数;以y轴为对称轴,则对应点的纵坐标相等,横坐标互为相反数.③在旋转变换中,一个图形绕原点旋转180°,则旋转前后两个图形上的对应点的横坐标与纵坐标分别互为相反数;④位似变换中,当以原点为位似中心时,变换前后两个图形上的对应点的横(或纵)坐标之比的绝对值等于相似比.[知识拓展] (1)以原点为位似中心的位似变换,其对应点的坐标关系可表示为(新图形与原图形的相似比为k):与P(x,y)位于位似中心同侧的对应点P1(kx,ky); 与P(x,y)位于位似中心异侧的对应点P2(-kx,-ky).当k>1时,是将图形扩大;当0
C.(-4,-4) D.(-4,-3)解析:∵△ABC的三边分别扩大一倍得到△A1B1C1(顶点均在格点上),它们是以P点为位似中心的位似图形,根据位似图形的性质,对应点的连线相交于一点,连接BB1,CC1,交点即是P点,如图所示,∴P点的坐标为(-4,-3).故选D.D2.已知线段AB和CD,依据下列点的坐标,能判断AB和CD是以原点为位似中心的位似图形的是 ( )
A.A(2,3),B(-1,1),C(4,3),D(-2,1)
B.A(1,-5),B(-1,-2),C(1,-10),D(-1,-4)
C.A(-4,5),B(2,-2),C(4,5),D(-2,-2)
D.A(2,0),B(-1,0),C(-4,0),D(2,0)解析:根据以原点为位似图形的坐标特征,可得C,D点横、纵坐标为A,B点横、纵坐标的同一个倍数的只有D.故选D.D 3.如图所示,原点O是△ABC和△A1B1C1的位似中心,点A(1,0)与A1(-2,0)是对应点,△ABC的面积是 ,则△A1B1C1的面积是 .?解析:∵原点O是△ABC和△A1B1C1的位似中心,点A(1,0)与A1(-2,0)是对应点,∴△ABC和△A1B1C1的相似比为 ,由相似三角形的面积比等于相似比的平方,得△A1B1C1的面积是 ×4=6.故填6.64.如图所示的小方格都是边长为1的正方形,△ABC的顶点都在小正方形的顶点上,请完成以下问题.
(1)请在方格纸上建立平面直角坐标系,使A(2,3),C(6,2),则B点的坐标为 ;?
(2)以原点O为位似中心,在第一象限内将△ABC放大为原来的2倍,画出放大后的△A'B'C'.解:(1)∵A(2,3),C(6,2),
∴可得如图所示的平面直角坐标系.
∴点B的坐标为(2,1).(2)∵以原点O为位似中心,在第一象限内将△ABC放大为原来的2倍,∴A' (4,6),B' (4,2),C' (12,4),
如图所示.
