27.3 位似(第1课时)课件
文档属性
| 名称 | 27.3 位似(第1课时)课件 |  | |
| 格式 | zip | ||
| 文件大小 | 189.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-30 08:52:38 | ||
图片预览

文档简介
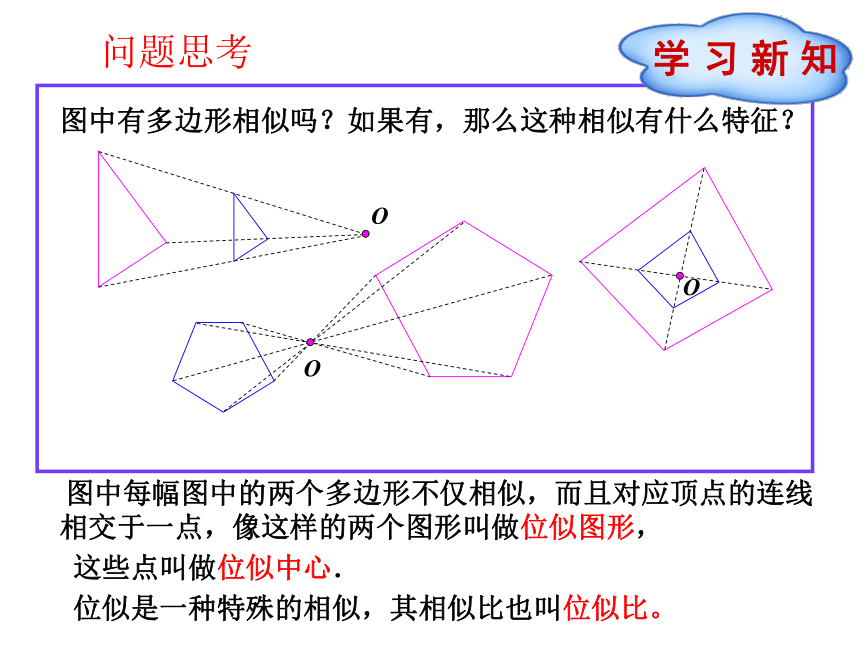
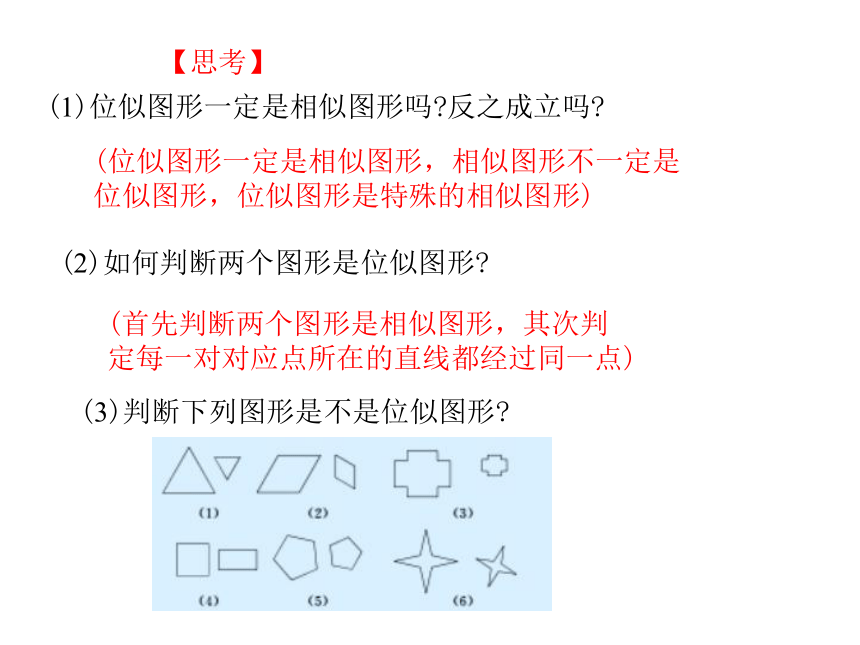
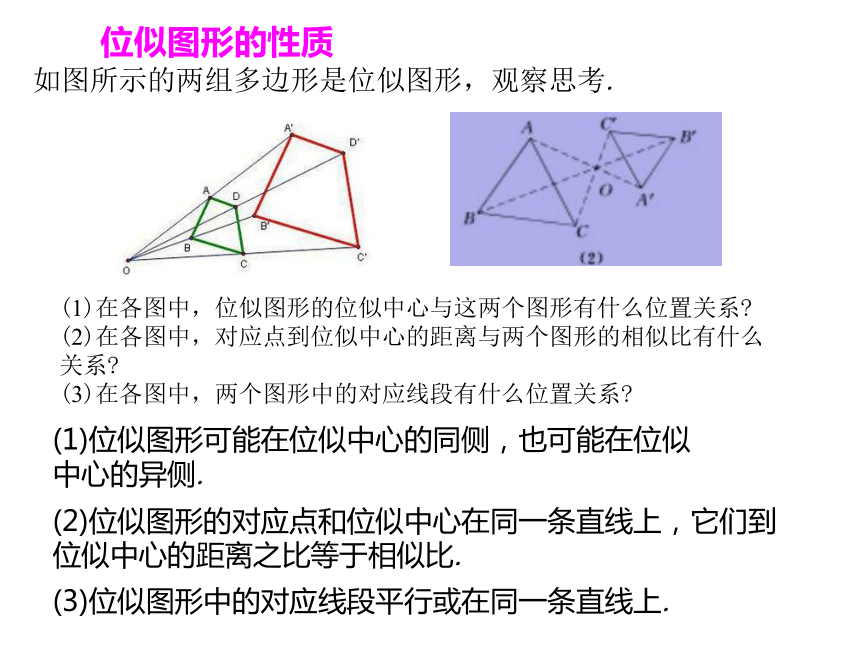
课件11张PPT。九年级数学·下 新课标 [人]第二十七章 反比例函数27.3 位似(第1课时)图中有多边形相似吗?如果有,那么这种相似有什么特征? 图中每幅图中的两个多边形不仅相似,而且对应顶点的连线相交于一点,像这样的两个图形叫做位似图形,OOO这些点叫做位似中心.位似是一种特殊的相似,其相似比也叫位似比。学 习 新 知问题思考【思考】(1)位似图形一定是相似图形吗?反之成立吗?(位似图形一定是相似图形,相似图形不一定是位似图形,位似图形是特殊的相似图形)(2)如何判断两个图形是位似图形?(首先判断两个图形是相似图形,其次判定每一对对应点所在的直线都经过同一点)(3)判断下列图形是不是位似图形?位似图形的性质如图所示的两组多边形是位似图形,观察思考.(1)在各图中,位似图形的位似中心与这两个图形有什么位置关系?
(2)在各图中,对应点到位似中心的距离与两个图形的相似比有什么关系?
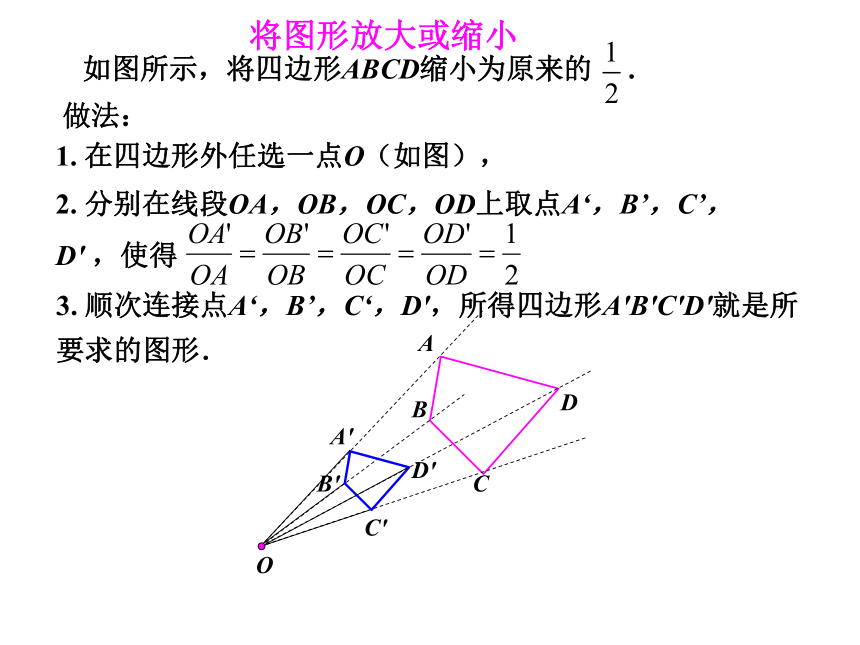
(3)在各图中,两个图形中的对应线段有什么位置关系?(3)位似图形中的对应线段平行或在同一条直线上.(1)位似图形可能在位似中心的同侧,也可能在位似中心的异侧.(2)位似图形的对应点和位似中心在同一条直线上,它们到位似中心的距离之比等于相似比.2. 分别在线段OA,OB,OC,OD上取点A‘,B’,C’,D' ,使得 3. 顺次连接点A‘,B’,C‘,D',所得四边形A'B'C'D'就是所要求的图形.ODABCA'B'C'D'做法:1. 在四边形外任选一点O(如图),将图形放大或缩小如图所示,将四边形ABCD缩小为原来的 .对于上面的问题,还有其他方法吗?如果在四边形外任选一个点O,分别在OA,OB,OC,OD的反向延长线上取A' ,B' 、C' 、D' ,使得 呢?如果点O取在四边形ABCD内部呢?分别画出这时得到的图形.ODABCA'B'C'D'ODABC[知识拓展](1)位似是一种具有特殊位置关系的相似.两个图形是位似图形,必定是相似图形,而两个图形是相似图形,不一定是位似图形.(2)位似中心可以在两个图形内部,两个图形之间,两个图形的同一侧,也可以在一个图形的一条边上或某一顶点上.(3)利用位似,可以将一个图形放大或缩小.(4)平行于三角形一边的直线与其他两边或两边的延长线相交,所构成的三角形与原三角形位似.(5)作位似图形时,要弄清相似比.(6)一般情况下,作已知图形的位似图形的结果不唯一.1.位似图形的概念.
2.位似图形与相似图形的关系:位似图形一定是相似图形,相似图形不一定是位似图形.
3.位似图形的性质:位似图形的对应点和位似中心在同一条直线上,它们到位似中心的距离之比等于相似比;位似图形中的对应线段平行或在同一条直线上.
4.画位似图形: 确定位似中心;对应点与位似中心的距离比相等.课堂小结检测反馈 解析:利用位似的定义可知,位似图形一定是相似图形,因为它是一种特殊的相似,但是相似图形不一定是位似图形,所以①错误,②正确;两个位似图形若全等,根据对应点一定相交于一点,可得到位似中心在两个图形之间,③正确;④若五边形ABCDE与五边形A'B'C'D'E'位似,则在五边形中连线组成的△ABC与△A'B'C',画出图形,可得它们也是位似的,④正确.所以②③④正确.故选C.1.下列说法:①相似图形一定是位似图形;②位似图形一定是相似图形;③两个位似图形若全等,则位似中心在两个图形之间;④若五边形ABCDE与五边形A'B'C'D'E'位似,则其中△ABC与△A'B'C'也是位似的,且相似比相等.其中正确的有( )
A.1个 B.2个 C.3个 D.4个C 解析:由△ABC和△A'B'C'是位似图形,且面积之比为1∶9,得△ABC和△A'B'C'的对应边AB与A'B'的比为1∶3.故选B. 2.△ABC和△A'B'C'是位似图形,且面积之比为1∶9,则△ABC和△A'B'C'的对应边AB和A'B'的比为 ( )
A.3:1 B.1:3 C.1:9 D.1:27B 解析:由△ABC与△A'B'C'是位似图形,且相似比是1∶2,得△ABC与△A'B'C'的周长比是1∶2,又△ABC的周长是3,所以△A'B'C'的周长为6.故填6.3.△ABC与△A'B'C'是位似图形,且△ABC与△A'B'C'的相似比是1∶2,已知△ABC的周长是3,则△A'B'C'的周长是 .?6 4.如图所示,已知△EFH和△MNK是位似图形,那么其位似中心是点 .?解析:因为位似图形的对应点的连线相交于一点,即位似中心,所以位似中心为B点.故填B.B5.如图所示,顶点都在网格线交点处的三角形叫做格点三角形,已知图中的每个小正方形的边长都是1个单位长度,在图中选择适当的位似中心,画一个与格点△DEF位似且相似比不等于1的格点三角形. 解:本题答案不唯一.如图所示的△DE'F'就是符合题意的一个三角形.
(2)在各图中,对应点到位似中心的距离与两个图形的相似比有什么关系?
(3)在各图中,两个图形中的对应线段有什么位置关系?(3)位似图形中的对应线段平行或在同一条直线上.(1)位似图形可能在位似中心的同侧,也可能在位似中心的异侧.(2)位似图形的对应点和位似中心在同一条直线上,它们到位似中心的距离之比等于相似比.2. 分别在线段OA,OB,OC,OD上取点A‘,B’,C’,D' ,使得 3. 顺次连接点A‘,B’,C‘,D',所得四边形A'B'C'D'就是所要求的图形.ODABCA'B'C'D'做法:1. 在四边形外任选一点O(如图),将图形放大或缩小如图所示,将四边形ABCD缩小为原来的 .对于上面的问题,还有其他方法吗?如果在四边形外任选一个点O,分别在OA,OB,OC,OD的反向延长线上取A' ,B' 、C' 、D' ,使得 呢?如果点O取在四边形ABCD内部呢?分别画出这时得到的图形.ODABCA'B'C'D'ODABC[知识拓展](1)位似是一种具有特殊位置关系的相似.两个图形是位似图形,必定是相似图形,而两个图形是相似图形,不一定是位似图形.(2)位似中心可以在两个图形内部,两个图形之间,两个图形的同一侧,也可以在一个图形的一条边上或某一顶点上.(3)利用位似,可以将一个图形放大或缩小.(4)平行于三角形一边的直线与其他两边或两边的延长线相交,所构成的三角形与原三角形位似.(5)作位似图形时,要弄清相似比.(6)一般情况下,作已知图形的位似图形的结果不唯一.1.位似图形的概念.
2.位似图形与相似图形的关系:位似图形一定是相似图形,相似图形不一定是位似图形.
3.位似图形的性质:位似图形的对应点和位似中心在同一条直线上,它们到位似中心的距离之比等于相似比;位似图形中的对应线段平行或在同一条直线上.
4.画位似图形: 确定位似中心;对应点与位似中心的距离比相等.课堂小结检测反馈 解析:利用位似的定义可知,位似图形一定是相似图形,因为它是一种特殊的相似,但是相似图形不一定是位似图形,所以①错误,②正确;两个位似图形若全等,根据对应点一定相交于一点,可得到位似中心在两个图形之间,③正确;④若五边形ABCDE与五边形A'B'C'D'E'位似,则在五边形中连线组成的△ABC与△A'B'C',画出图形,可得它们也是位似的,④正确.所以②③④正确.故选C.1.下列说法:①相似图形一定是位似图形;②位似图形一定是相似图形;③两个位似图形若全等,则位似中心在两个图形之间;④若五边形ABCDE与五边形A'B'C'D'E'位似,则其中△ABC与△A'B'C'也是位似的,且相似比相等.其中正确的有( )
A.1个 B.2个 C.3个 D.4个C 解析:由△ABC和△A'B'C'是位似图形,且面积之比为1∶9,得△ABC和△A'B'C'的对应边AB与A'B'的比为1∶3.故选B. 2.△ABC和△A'B'C'是位似图形,且面积之比为1∶9,则△ABC和△A'B'C'的对应边AB和A'B'的比为 ( )
A.3:1 B.1:3 C.1:9 D.1:27B 解析:由△ABC与△A'B'C'是位似图形,且相似比是1∶2,得△ABC与△A'B'C'的周长比是1∶2,又△ABC的周长是3,所以△A'B'C'的周长为6.故填6.3.△ABC与△A'B'C'是位似图形,且△ABC与△A'B'C'的相似比是1∶2,已知△ABC的周长是3,则△A'B'C'的周长是 .?6 4.如图所示,已知△EFH和△MNK是位似图形,那么其位似中心是点 .?解析:因为位似图形的对应点的连线相交于一点,即位似中心,所以位似中心为B点.故填B.B5.如图所示,顶点都在网格线交点处的三角形叫做格点三角形,已知图中的每个小正方形的边长都是1个单位长度,在图中选择适当的位似中心,画一个与格点△DEF位似且相似比不等于1的格点三角形. 解:本题答案不唯一.如图所示的△DE'F'就是符合题意的一个三角形.
