28.1 锐角三角函数(第1课时)课件
文档属性
| 名称 | 28.1 锐角三角函数(第1课时)课件 |  | |
| 格式 | zip | ||
| 文件大小 | 246.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-30 09:08:00 | ||
图片预览





文档简介
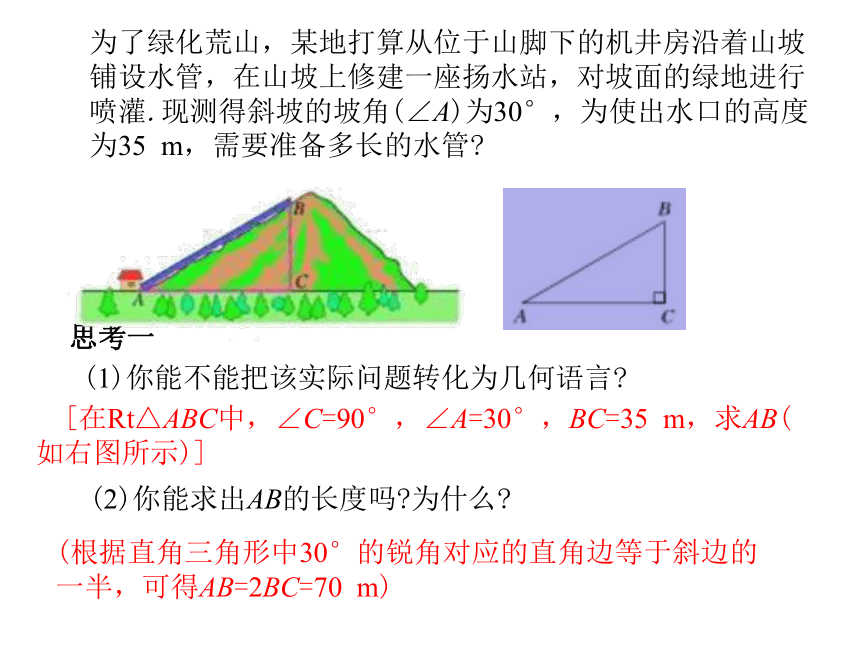
课件16张PPT。九年级数学·下 新课标[人] 第二十八章 锐角三角函数28.1 锐角三角函数(第1课时)学 习 新 知问题思考 意大利比萨斜塔在1350年落成时就已倾斜,其塔顶中心点偏离垂直中心线2.1 m.1972年比萨地区发生地震,这座高54.5 m的斜塔在大幅度摇摆后仍巍然屹立,但塔顶中心点偏离垂直中心线增至5.2 m,而且还在继续倾斜,有倒塌的危险.当地从1990年起对斜塔维修纠偏,2001年竣工,此时塔顶中心点偏离垂直中心线的距离比纠偏前减少了43.8 cm.你能用塔身中心线与垂直中心线所成的角来描述比萨斜塔的倾斜程度吗?为了绿化荒山,某地打算从位于山脚下的机井房沿着山坡铺设水管,在山坡上修建一座扬水站,对坡面的绿地进行喷灌.现测得斜坡的坡角(∠A)为30°,为使出水口的高度为35 m,需要准备多长的水管? [在Rt△ABC中,∠C=90°,∠A=30°,BC=35 m,求AB(如右图所示)]思考一(1)你能不能把该实际问题转化为几何语言?(2)你能求出AB的长度吗?为什么?(根据直角三角形中30°的锐角对应的直角边等于斜边的一半,可得AB=2BC=70 m)(1)如下图所示,任意画一个Rt△ABC,使∠C=90°,∠A=45°,你能计算出∠A的对边与斜边的比 吗?
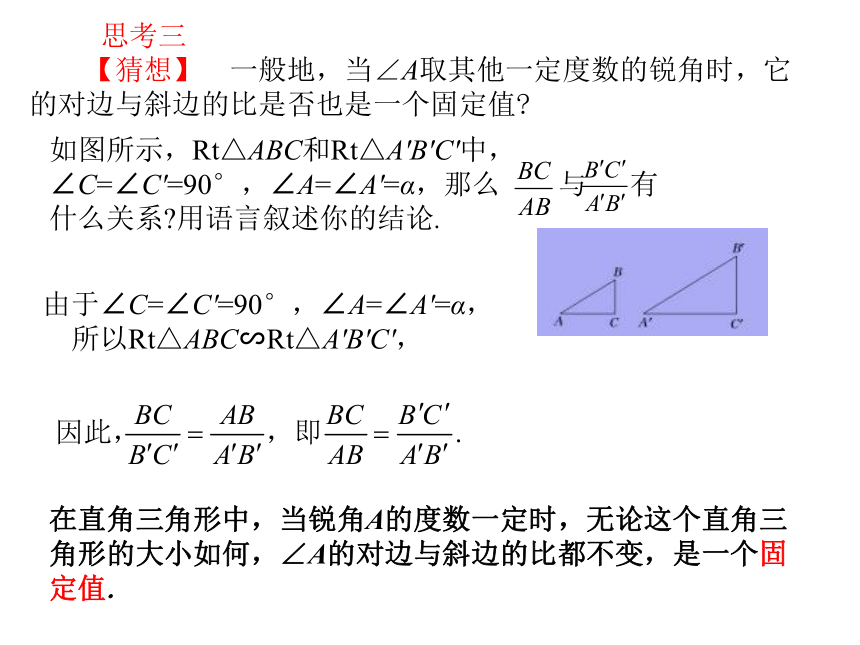
(2)通过计算,你能得到什么结论?【结论】 在直角三角形中,如果一个锐角等于45°,无论这个直角三角形大小如何,这个角的对边与斜边的比都等于 .思考二(教材例1)如图所示,在Rt△ABC中,∠C=90°,求sin A和sin B的值.思考:
(1)求sin A实际上要确定什么?依据是什么?sin B呢?
(2)sin A,sin B的对边和斜边是已知的吗?
(3)直角三角形中已知两边如何求三角形的第三边?解: (1)Rt△ABC中,因此(2)在Rt△ABC中,因此ABCABC34135 (1)正弦是一个比值,没有单位.
(2)正弦值只与角的大小有关,与三角形的大小无关.
(3)sin A是一个整体符号,不能写成sin ·A.
(4)当用三个字母表示角时,角的符号“∠”不能省略,如sin∠ABC.
(5)sin2A表示(sin A)2,不能写成sin A2.[知识拓展] 检测反馈1.如图所示,△ABC的顶点都是正方形网格(每个小正方形的边长均为1)中的格点,则sin∠ABC等于 ( )解析:如图所示,过点A向BC引垂线,与BC的延长线交于点D.在Rt△ABD中,AD=2,BD=4,∴AB= ,∴sin∠ABC= .故选C.CA. B. C. D. 2.把△ABC三边的长度都扩大为原来的3倍,则锐角A的正弦值( )
A.不变
B.缩小为原来的
C.扩大为原来的3倍
D.不能确定解析:因为△ABC三边的长度都扩大为原来的3倍所得的三角形与原三角形相似,所以锐角A的大小没改变,所以锐角A的正弦值也不变.故选A.A4.如图所示,在菱形ABCD中,DE⊥AB,垂足为E,DE=8 cm,sin A= ,则菱形ABCD的面积是 cm2.?解析:在菱形ABCD中,DE⊥AB,在Rt△DEA中,DE=8 cm,sin A= ,则 ,则AD=10 cm.所以AB=AD=10 cm,所以菱形ABCD的面积=DE×AB=8×10=80(cm2).故填80.805.在Rt△ABC中,∠C=90°,BC=6,且sin B= ,试分别求出AC,AB的值.解:在Rt△ABC中,∠C=90°,
∴sin B= .
设AC=3x,则AB=5x.
又AB2=AC2+BC2,
∴(5x)2=(3x)2+62=9x2+36,
即25x2=9x2+36,
∴x= ,∴AC=3x= ,AB=5x= .
(2)通过计算,你能得到什么结论?【结论】 在直角三角形中,如果一个锐角等于45°,无论这个直角三角形大小如何,这个角的对边与斜边的比都等于 .思考二(教材例1)如图所示,在Rt△ABC中,∠C=90°,求sin A和sin B的值.思考:
(1)求sin A实际上要确定什么?依据是什么?sin B呢?
(2)sin A,sin B的对边和斜边是已知的吗?
(3)直角三角形中已知两边如何求三角形的第三边?解: (1)Rt△ABC中,因此(2)在Rt△ABC中,因此ABCABC34135 (1)正弦是一个比值,没有单位.
(2)正弦值只与角的大小有关,与三角形的大小无关.
(3)sin A是一个整体符号,不能写成sin ·A.
(4)当用三个字母表示角时,角的符号“∠”不能省略,如sin∠ABC.
(5)sin2A表示(sin A)2,不能写成sin A2.[知识拓展] 检测反馈1.如图所示,△ABC的顶点都是正方形网格(每个小正方形的边长均为1)中的格点,则sin∠ABC等于 ( )解析:如图所示,过点A向BC引垂线,与BC的延长线交于点D.在Rt△ABD中,AD=2,BD=4,∴AB= ,∴sin∠ABC= .故选C.CA. B. C. D. 2.把△ABC三边的长度都扩大为原来的3倍,则锐角A的正弦值( )
A.不变
B.缩小为原来的
C.扩大为原来的3倍
D.不能确定解析:因为△ABC三边的长度都扩大为原来的3倍所得的三角形与原三角形相似,所以锐角A的大小没改变,所以锐角A的正弦值也不变.故选A.A4.如图所示,在菱形ABCD中,DE⊥AB,垂足为E,DE=8 cm,sin A= ,则菱形ABCD的面积是 cm2.?解析:在菱形ABCD中,DE⊥AB,在Rt△DEA中,DE=8 cm,sin A= ,则 ,则AD=10 cm.所以AB=AD=10 cm,所以菱形ABCD的面积=DE×AB=8×10=80(cm2).故填80.805.在Rt△ABC中,∠C=90°,BC=6,且sin B= ,试分别求出AC,AB的值.解:在Rt△ABC中,∠C=90°,
∴sin B= .
设AC=3x,则AB=5x.
又AB2=AC2+BC2,
∴(5x)2=(3x)2+62=9x2+36,
即25x2=9x2+36,
∴x= ,∴AC=3x= ,AB=5x= .
