28.1 锐角三角函数(第2课时)课件
文档属性
| 名称 | 28.1 锐角三角函数(第2课时)课件 |  | |
| 格式 | zip | ||
| 文件大小 | 200.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-30 09:23:45 | ||
图片预览



文档简介
课件10张PPT。九年级数学·下 新课标[人]第二十八章 锐角三角函数28.2 锐角三角函数(第2课时)学 习 新 知问题思考观察两个大小不同的三角板,当角是30°,45°,60°时,它们的邻边与斜边、对边与邻边的比有什么规律?谈谈你的看法. 1.在直角三角形中,当锐角的度数一定时,无论这个直角三角形的大小如何,这个角的邻边与斜边的比都是一个固定值.
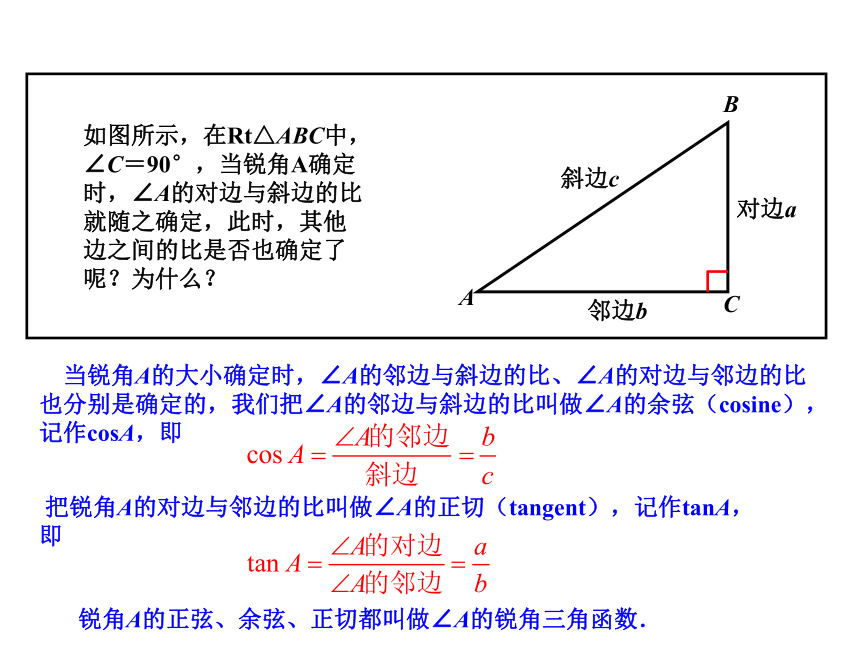
2.在直角三角形中,当锐角的度数一定时,无论这个直角三角形的大小如何,这个角的对边与邻边的比都是一个固定值.如图所示,在Rt△ABC中,∠C=90°,当锐角A确定时,∠A的对边与斜边的比就随之确定,此时,其他边之间的比是否也确定了呢?为什么? 当锐角A的大小确定时,∠A的邻边与斜边的比、∠A的对边与邻边的比也分别是确定的,我们把∠A的邻边与斜边的比叫做∠A的余弦(cosine),记作cosA,即 把锐角A的对边与邻边的比叫做∠A的正切(tangent),记作tanA,即 锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数.(教材例2)如图所示,在Rt△ABC中,∠C=90°,AB=10,BC=6,求sin A,cos A,tan A的值.【思考】
(1)根据余弦、正切的定义,要求cos A,tan A的值必须求出哪条边的长?
(2)怎样求出AC的长?(补充拓展)如图所示,在Rt△ABC中,∠C=90°,BC=6,sin A= ,求cos A,tan B的值.【解析】(1)已知sin A和BC的值,根据正弦定义,可以求出三角形的哪条边长?(2)你能不能求出三角形的第三条边长? (3)根据余弦、正切定义,你能求出cos A,tan B的值吗?(4)当用三个字母表示角时,角的符号“∠”不能省略,如tan∠ABC.[知识拓展] (1)余弦和正切都是一个比值,没有单位.(2)余弦值和正切值只与角的大小有关,而与三角形的大小无关.(3)cos A,tan A都是一个整体符号,不能写成cos·A,tan·A.
2.在直角三角形中,当锐角的度数一定时,无论这个直角三角形的大小如何,这个角的对边与邻边的比都是一个固定值.如图所示,在Rt△ABC中,∠C=90°,当锐角A确定时,∠A的对边与斜边的比就随之确定,此时,其他边之间的比是否也确定了呢?为什么? 当锐角A的大小确定时,∠A的邻边与斜边的比、∠A的对边与邻边的比也分别是确定的,我们把∠A的邻边与斜边的比叫做∠A的余弦(cosine),记作cosA,即 把锐角A的对边与邻边的比叫做∠A的正切(tangent),记作tanA,即 锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数.(教材例2)如图所示,在Rt△ABC中,∠C=90°,AB=10,BC=6,求sin A,cos A,tan A的值.【思考】
(1)根据余弦、正切的定义,要求cos A,tan A的值必须求出哪条边的长?
(2)怎样求出AC的长?(补充拓展)如图所示,在Rt△ABC中,∠C=90°,BC=6,sin A= ,求cos A,tan B的值.【解析】(1)已知sin A和BC的值,根据正弦定义,可以求出三角形的哪条边长?(2)你能不能求出三角形的第三条边长? (3)根据余弦、正切定义,你能求出cos A,tan B的值吗?(4)当用三个字母表示角时,角的符号“∠”不能省略,如tan∠ABC.[知识拓展] (1)余弦和正切都是一个比值,没有单位.(2)余弦值和正切值只与角的大小有关,而与三角形的大小无关.(3)cos A,tan A都是一个整体符号,不能写成cos·A,tan·A.
