复数复习课

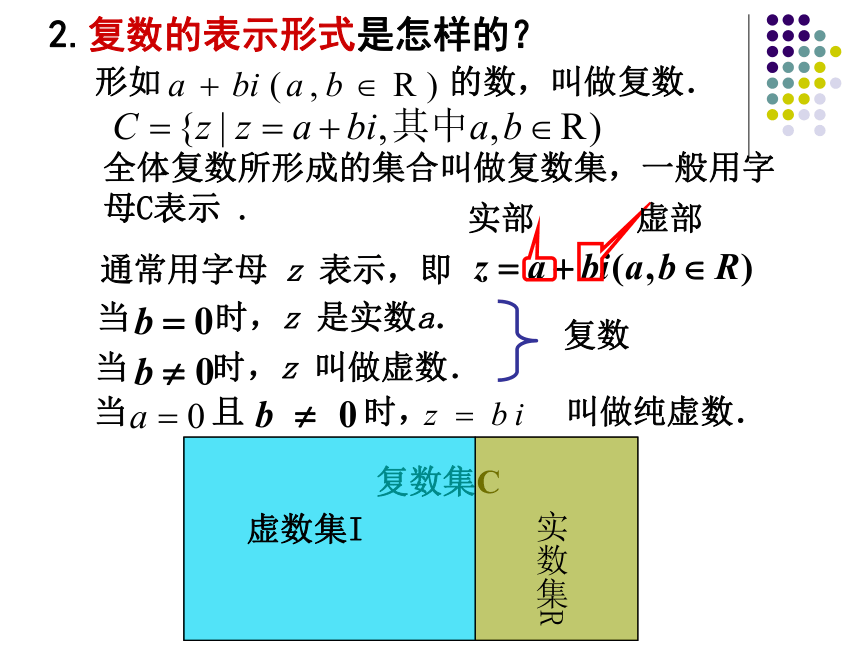
课件17张PPT。第三章 复数根据对虚数单位i的运算规定易知： 1.虚数单位是怎样定义的？ 一、基本知识虚数单位，规定：（2）实数可以与它进行四则运算，进行四则运算时，原有的加、乘运算律仍然成立．形如 的数，叫做复数． 全体复数所形成的集合叫做复数集，一般用字母C表示 . 2.复数的表示形式是怎样的？当 时，z 是实数a．当 时，z 叫做虚数．当 且 时， 叫做纯虚数．例1：实数m取什么值时，复数 是
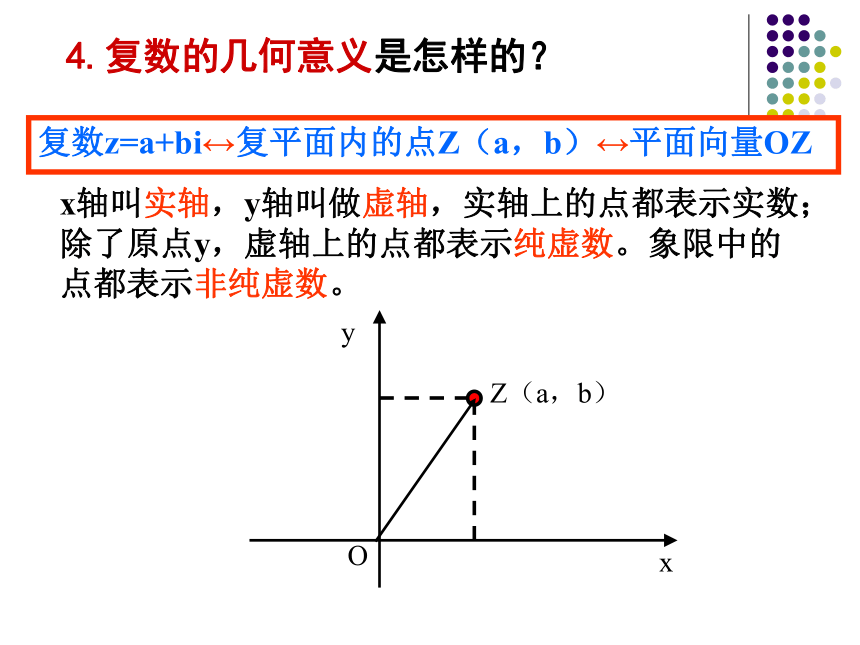
（1）实数？ （2）虚数？ （3）纯虚数？(口答）解：（1）当 ，即 时，复数z是实数．（2）当 ，即 时，复数z是虚数．（3）当 ，且 ，即 时，复数z 是纯虚数．如果两个复数的实部和虚部分别相等，那么我们就说这两个复数相等．即如果 ，那么例2 已知 ，其中 ，求解：更具复数相等的定义，得方程组所以3.两复数相等的充要条件是什么？x轴叫实轴，y轴叫做虚轴，实轴上的点都表示实数；除了原点y，虚轴上的点都表示纯虚数。象限中的点都表示非纯虚数。复数z=a+bi?复平面内的点Z（a，b）?平面向量OZ4.复数的几何意义是怎样的？5、复数的加法法则6、复数的减法法则（a+bi）-（c+di）=（a-c）+（b-d）i。注：两个复数相加（减）就是把实部与实部、虚部与虚部分别相加（减），即
（a+bi）±（c+di）=（a ± c） + （b±d）i（a+bi）+（c+di）=（a+c）+（b+d）i7、复数的乘法z1·z2=(a+bi)(c+di)=注：1、复数的乘法与多项式的乘法类似，但必须在所得的结果中把i2 换成-1，并把实部与虚部分开。ac+bci+adi+bdi2=(ac-bd)+(ad+bc)i8、复数的除法（a+bi）÷ （c+di) 或9、补充概念。例3：设w= 求证：
① 1+w+w2=o ②w3=1例4： i 2002+( + i)8(4)复数的模可以比较大小，一般地，两个复数不能比较大小，除非两个复数都是实数才可以比较大小。典型例题：一、代数运算例6：实数m取什么值时，复数
对应的点
（1）位于第一、三象限？
（2）位于第四象限？例7：（A）1 （B）－1 （C）2 （D）－2解：z2－z + 1＝0 ， 即(z+1)·(z2－z+1)＝0∴ z1111＝(z3)370·z＝z
z2222＝(z1111)2＝z2∴ ，故（A）正确．即z3+1＝0 ∴ z3＝－1 以下同解法1．例9.如果复数 （其中i为虚数单位，b为实数）
的实部和虚部互为相反数，那么b等于
A. B. C.－ D.2
解析： = =
∴2－2b=b+4，b=－ .
答案：C例10当 ＜m＜1时，复数z=(3m－2)+(m－1)i
在复平面上对应的点位于
A.第一象限 B.第二象限
C.第三象限 D.第四象限解析：z对应的点为(3m－2，m－1)，
∵ ＜m＜1，
∴0＜3m－2＜1，－ ＜m－1＜0.
答案：D 例11.设f(n)=( )n+( )n(n∈Z)，则集合
｛x｜x=f(n)｝中元素的个数是
A.1 B.2 C.3 D.无穷多个解析：∵f(n)=in+(－i)n，
∴f(0)=2，f(1)=i－i=0，f(2)=－1－1=－2，f(3)=－i+i=0.
∴｛x｜x=f(n)｝=｛－2，0，2｝.
答案：C 例12.复数z满足z· +z+ =3，则z对应点的轨迹是____________.
解析：设z=x+yi(x、y∈R)，则x2+y2+2x=3表示圆.
答案：以点（－1，0）为圆心，2为半径的圆例13若复数z满足 ，则 的值为 . 例14 复数z满足z· +z+ =3，则z对应点的轨迹是____________.
解析：设z=x+yi(x、y∈R)，则x2+y2+2x=3表示圆.
答案：以点（－1，0）为圆心，2为半径的圆典型例题：二、复数几何意义的运用例15 若 ，则 的最大值为 . 例16 若 ，若使 的最小，求b的值。 例17 设复数z满足 ，试求 的最大值和最小值。