复数代数形式的加、减运算及其几何意义
文档属性
| 名称 | 复数代数形式的加、减运算及其几何意义 |  | |
| 格式 | zip | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-05-14 10:16:00 | ||
图片预览






文档简介
(共14张PPT)
1.复数加、减法的运算法则:
已知两复数z1=a+bi, z2=c+di(a,b,c,d是实数)
即:两个复数相加(减)就是
实部与实部,虚部与虚部分别相加(减).
(1)加法法则:z1+z2=(a+c)+(b+d)i;
(2)减法法则:z1-z2=(a-c)+(b-d)i.
(a+bi )±(c+di) = (a±c) + (b±d)i
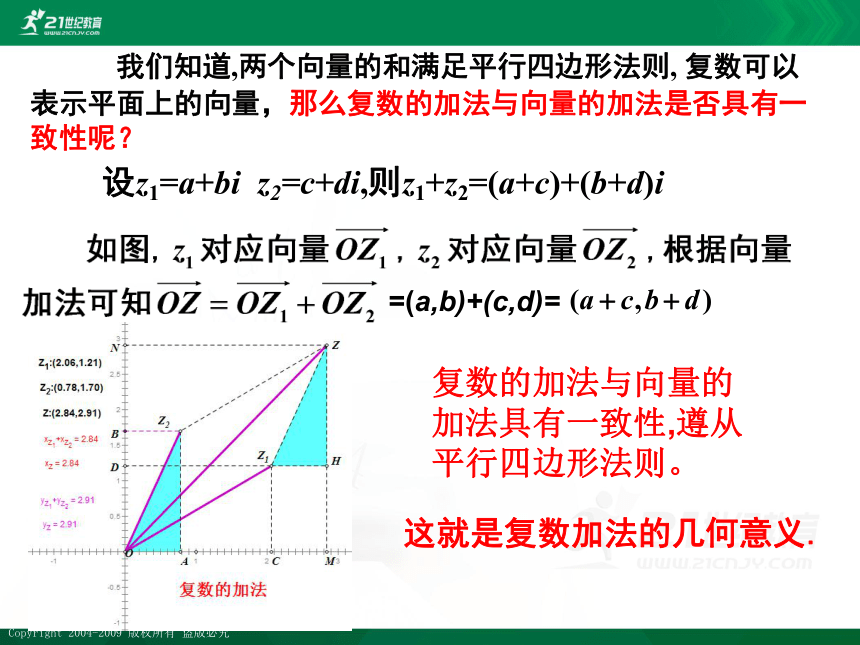
我们知道,两个向量的和满足平行四边形法则, 复数可以表示平面上的向量,那么复数的加法与向量的加法是否具有一致性呢?
设z1=a+bi z2=c+di,则z1+z2=(a+c)+(b+d)i
这就是复数加法的几何意义.
=(a,b)+(c,d)=
复数的加法与向量的加法具有一致性,遵从平行四边形法则。
类似地,复数减法:
Z1(a,b)
Z2(c,d)
O
y
x
Z
OZ1-OZ2
这就是复数减法的几何意义.
复数的减法为对应向量的减法
广21世纪数痘
27世纪数育
www.
1.复数的加法与减法
(1)复数的加、减法法则
(a+i)+(c+di)=
(a-bi)-(cdi)
即两个复数相加(减),就是实部与实部,虚部与虚部分别
(a-c)(bd)i
(ac)+(b-d)i
相加(减)
(2)复数加法的运算定律
复数的加法满足交换律、结合律,即对任何1,2,3∈C,
有1十2=,(1十2)十3=
同类变式…
…(即时突破,举一反三)
Tong Lei Bian Shi
1.计算:
(1)(1+V2i)+(-2-3i)-(3-2i);
(2)2i-[(3+2i)-(-1+3i)];
(3)(a+2bi)-(3a-4i)-5i(a,b∈R).
解:(1)原式=[-1十(2-3)门-(3-2i)
=-4+(2+V2-3)i.
(2)原式=2i一(4-i)=-4十3i.
(3)原式=-2u+6i-5i=-2a+(6b-5)i.
Z1(2.06,1.21)
2.5
Z20.78,1.70)
Z:(2.84,2.91)
z,+22=2.84
B
1.5
Z
Xz=2.84
H
yz,+y22=2.91
0.5
yz=2.91
++++十十十十+十十++0十十+十十十4+++十十+十+十++++十++十叶+H
Me
-0.5
复数的加法
1.复数加、减法的运算法则:
已知两复数z1=a+bi, z2=c+di(a,b,c,d是实数)
即:两个复数相加(减)就是
实部与实部,虚部与虚部分别相加(减).
(1)加法法则:z1+z2=(a+c)+(b+d)i;
(2)减法法则:z1-z2=(a-c)+(b-d)i.
(a+bi )±(c+di) = (a±c) + (b±d)i
我们知道,两个向量的和满足平行四边形法则, 复数可以表示平面上的向量,那么复数的加法与向量的加法是否具有一致性呢?
设z1=a+bi z2=c+di,则z1+z2=(a+c)+(b+d)i
这就是复数加法的几何意义.
=(a,b)+(c,d)=
复数的加法与向量的加法具有一致性,遵从平行四边形法则。
类似地,复数减法:
Z1(a,b)
Z2(c,d)
O
y
x
Z
OZ1-OZ2
这就是复数减法的几何意义.
复数的减法为对应向量的减法
广21世纪数痘
27世纪数育
www.
1.复数的加法与减法
(1)复数的加、减法法则
(a+i)+(c+di)=
(a-bi)-(cdi)
即两个复数相加(减),就是实部与实部,虚部与虚部分别
(a-c)(bd)i
(ac)+(b-d)i
相加(减)
(2)复数加法的运算定律
复数的加法满足交换律、结合律,即对任何1,2,3∈C,
有1十2=,(1十2)十3=
同类变式…
…(即时突破,举一反三)
Tong Lei Bian Shi
1.计算:
(1)(1+V2i)+(-2-3i)-(3-2i);
(2)2i-[(3+2i)-(-1+3i)];
(3)(a+2bi)-(3a-4i)-5i(a,b∈R).
解:(1)原式=[-1十(2-3)门-(3-2i)
=-4+(2+V2-3)i.
(2)原式=2i一(4-i)=-4十3i.
(3)原式=-2u+6i-5i=-2a+(6b-5)i.
Z1(2.06,1.21)
2.5
Z20.78,1.70)
Z:(2.84,2.91)
z,+22=2.84
B
1.5
Z
Xz=2.84
H
yz,+y22=2.91
0.5
yz=2.91
++++十十十十+十十++0十十+十十十4+++十十+十+十++++十++十叶+H
Me
-0.5
复数的加法
