22.1 待定系数法求二次函数解析式 课件
文档属性
| 名称 | 22.1 待定系数法求二次函数解析式 课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 179.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-30 20:33:57 | ||
图片预览



文档简介
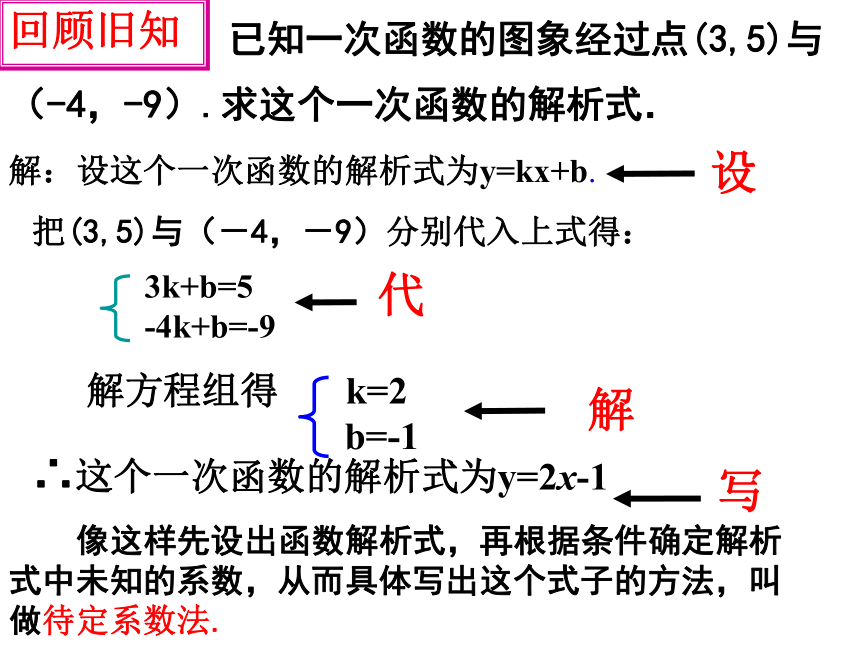
课件17张PPT。第22章 二次函数教师:杨永铭二次函数的解析式图象和性质 像这样先设出函数解析式,再根据条件确定解析式中未知的系数,从而具体写出这个式子的方法,叫做待定系数法.解:设这个一次函数的解析式为y=kx+b.设代解写把(3,5)与(-4,-9)分别代入上式得:∴这个一次函数的解析式为y=2x-1回顾旧知 已知一次函数的图象经过点(3,5)与(-4,-9).求这个一次函数的解析式. 已知一个二次函数的图象过点(0,-3) (4,5)(-1, 0)三点,求这个函数的解析式.例1:变式
x=0时,y= -3;
x=4时,y=5;
x=-1时,y=0;
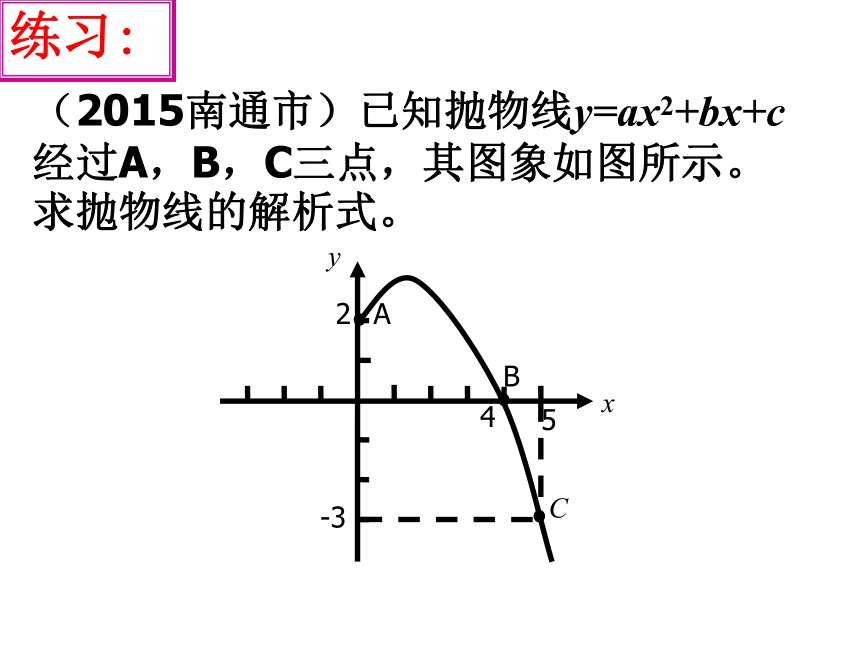
(2015南通市)已知抛物线y=ax2+bx+c经过A,B,C三点,其图象如图所示。求抛物线的解析式。练习:解:设所求的二次函数为 已知抛物线的顶点为(1,-4),
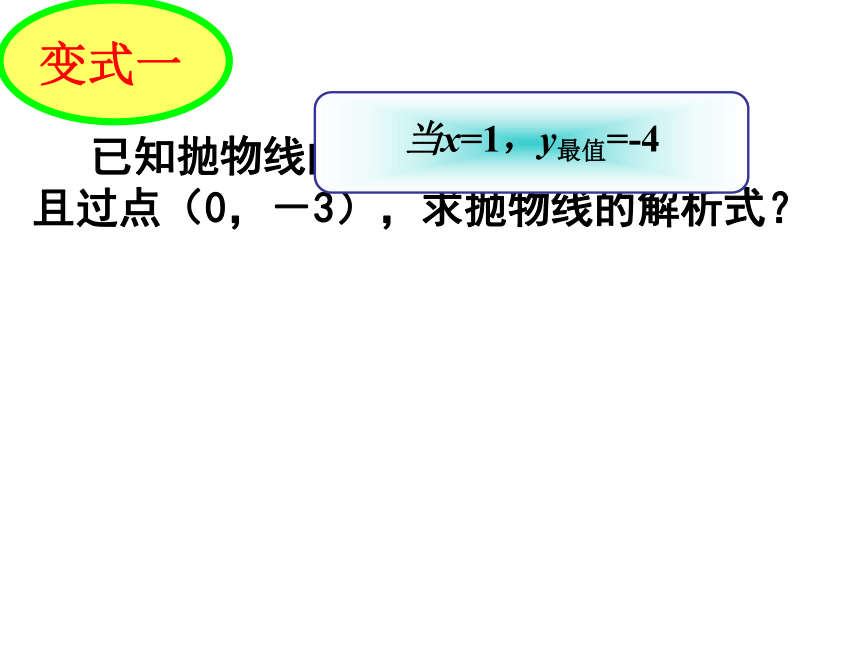
且过点(0,-3),求抛物线的解析式?点( 0,-3)在抛物线上a-4=-3, ∴所求的抛物线解析式为 y=(x-1)2-4∵∴∴ a=1y=a(x-1)2 -4例2:即 y=x2-2x-3变式一 已知抛物线的顶点为(1,-4),
且过点(0,-3),求抛物线的解析式?当x=1,y最值=-4 已知一个二次函数的图象过点(0,-3)(4,5)
对称轴为直线x=1,求这个函数的解析式.思考:怎样设二次函数解析式把(0,-3)(4,5)代入得二次函数解析式为:变式二a+k=-39a+k=5解得a=1k=-4即 y=x2-2x-3解:设所求的二次函数为 y=ax2+bx+cc=-3
16a+4b+c=5 已知一个二次函数的图象过点(0,-3)(4,5)
对称轴为直线x=1,求这个函数的解析式.对称轴为直线x=1=1依题意得变式二解得a=1
b=-2
c=-3∴所求的抛物线解析式为 y=x2-2x-3
已知抛物线过点A(-3,0)B(1,0)
C(2,5),求该抛物线的解析式。
9a-3b+c=0
a+b+c=0
4a+2b+c=5例3: 已知抛物线与x轴的两个交点坐标为( x1 ,0),( x2 ,0)时,二次函数解析式可以写为y=a(x- x1)(x- x2),称为二次函数的交点式(或两根式),其中x1 ,x2 为两交点的横坐标。知识补充:二次函数的交点式 已知抛物线过点A(-3,0)B(1,0)
C(2,5),求该抛物线的解析式。
解:设所求的二次函数为
y=a(x+3)(x-1)把C(2,5)代入得
5a=5 解得 a=1∴所求的抛物线解析式为
y=(x+3)(x-1)即y=x2+2x-3变式训练 已知抛物线的顶点为A(-1,-4),又知抛物线与x 轴的两个交点B、C间的距离为4,求其解析式。解:∵抛物线与x轴两交点距离为4,对称轴为x=-1∴点B(1,0)点C(-3,0)已知三个点坐标或三对对应值,选择一般式已知顶点坐标或对称轴或最值,选择顶点式 已知抛物线与x轴的两交点坐标,选择交点式二次函数常用的几种解析式
一般式 y=ax2+bx+c (a≠0)
顶点式 y=a(x-h)2+k (a≠0)
交点式 y=a(x-x1)(x-x2) (a≠0)
小结:作业1、课本42页第10题(2)(3)
2、《课计划》43页;37页第10题;39页第15题。1、(2014?德州)如图,在平面直角坐标系中,已知点A的坐标是(4,0),并且OA=OC=4OB,A,B,C三点都在抛物线上.求抛物线的解析式.【中考链接】 2、 已知:抛物线y=ax2+bx+c的图象如图所示:
(1)求此抛物线的解析式;
(2)当x取何值时,y>0?
(3)将抛物线作怎样的一次
平移,才能使它与坐标轴仅有
两个交点,并写出此时抛物线
的解析式。xyoABDC-15-2.5
x=0时,y= -3;
x=4时,y=5;
x=-1时,y=0;
(2015南通市)已知抛物线y=ax2+bx+c经过A,B,C三点,其图象如图所示。求抛物线的解析式。练习:解:设所求的二次函数为 已知抛物线的顶点为(1,-4),
且过点(0,-3),求抛物线的解析式?点( 0,-3)在抛物线上a-4=-3, ∴所求的抛物线解析式为 y=(x-1)2-4∵∴∴ a=1y=a(x-1)2 -4例2:即 y=x2-2x-3变式一 已知抛物线的顶点为(1,-4),
且过点(0,-3),求抛物线的解析式?当x=1,y最值=-4 已知一个二次函数的图象过点(0,-3)(4,5)
对称轴为直线x=1,求这个函数的解析式.思考:怎样设二次函数解析式把(0,-3)(4,5)代入得二次函数解析式为:变式二a+k=-39a+k=5解得a=1k=-4即 y=x2-2x-3解:设所求的二次函数为 y=ax2+bx+cc=-3
16a+4b+c=5 已知一个二次函数的图象过点(0,-3)(4,5)
对称轴为直线x=1,求这个函数的解析式.对称轴为直线x=1=1依题意得变式二解得a=1
b=-2
c=-3∴所求的抛物线解析式为 y=x2-2x-3
已知抛物线过点A(-3,0)B(1,0)
C(2,5),求该抛物线的解析式。
9a-3b+c=0
a+b+c=0
4a+2b+c=5例3: 已知抛物线与x轴的两个交点坐标为( x1 ,0),( x2 ,0)时,二次函数解析式可以写为y=a(x- x1)(x- x2),称为二次函数的交点式(或两根式),其中x1 ,x2 为两交点的横坐标。知识补充:二次函数的交点式 已知抛物线过点A(-3,0)B(1,0)
C(2,5),求该抛物线的解析式。
解:设所求的二次函数为
y=a(x+3)(x-1)把C(2,5)代入得
5a=5 解得 a=1∴所求的抛物线解析式为
y=(x+3)(x-1)即y=x2+2x-3变式训练 已知抛物线的顶点为A(-1,-4),又知抛物线与x 轴的两个交点B、C间的距离为4,求其解析式。解:∵抛物线与x轴两交点距离为4,对称轴为x=-1∴点B(1,0)点C(-3,0)已知三个点坐标或三对对应值,选择一般式已知顶点坐标或对称轴或最值,选择顶点式 已知抛物线与x轴的两交点坐标,选择交点式二次函数常用的几种解析式
一般式 y=ax2+bx+c (a≠0)
顶点式 y=a(x-h)2+k (a≠0)
交点式 y=a(x-x1)(x-x2) (a≠0)
小结:作业1、课本42页第10题(2)(3)
2、《课计划》43页;37页第10题;39页第15题。1、(2014?德州)如图,在平面直角坐标系中,已知点A的坐标是(4,0),并且OA=OC=4OB,A,B,C三点都在抛物线上.求抛物线的解析式.【中考链接】 2、 已知:抛物线y=ax2+bx+c的图象如图所示:
(1)求此抛物线的解析式;
(2)当x取何值时,y>0?
(3)将抛物线作怎样的一次
平移,才能使它与坐标轴仅有
两个交点,并写出此时抛物线
的解析式。xyoABDC-15-2.5
同课章节目录
