青岛版九年级上数学第三单元对圆的进一步认识复习题(含答案)
文档属性
| 名称 | 青岛版九年级上数学第三单元对圆的进一步认识复习题(含答案) | 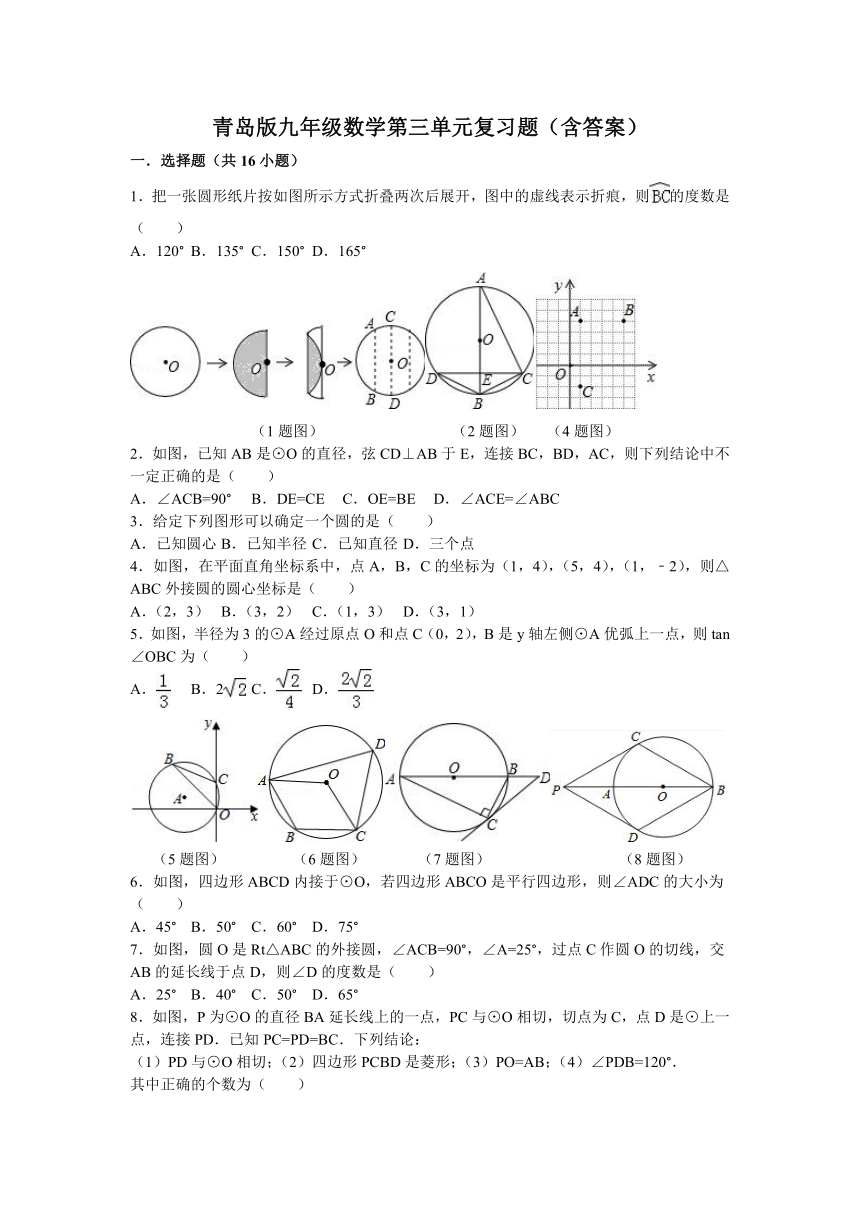 | |
| 格式 | zip | ||
| 文件大小 | 153.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-31 11:25:02 | ||
图片预览


文档简介
青岛版九年级数学第三单元复习题(含答案)
一.选择题(共16小题)
1.把一张圆形纸片按如图所示方式折叠两次后展开,图中的虚线表示折痕,则的度数是( )
A.120°
B.135°
C.150°
D.165°
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
(1题图)
(2题图)
(4题图)
2.如图,已知AB是⊙O的直径,弦CD⊥AB于E,连接BC,BD,AC,则下列结论中不一定正确的是( )
A.∠ACB=90°
B.DE=CE
C.OE=BE
D.∠ACE=∠ABC
3.给定下列图形可以确定一个圆的是( )
A.已知圆心
B.已知半径
C.已知直径
D.三个点
4.如图,在平面直角坐标系中,点A,B,C的坐标为(1,4),(5,4),(1,﹣2),则△ABC外接圆的圆心坐标是( )
A.(2,3)
B.(3,2)
C.(1,3)
D.(3,1)
5.如图,半径为3的⊙A经过原点O和点C(0,2),B是y轴左侧⊙A优弧上一点,则tan∠OBC为( )
A.
B.2
C.
D.
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
(5题图)
(6题图)
(7题图)
(8题图)
6.如图,四边形ABCD内接于⊙O,若四边形ABCO是平行四边形,则∠ADC的大小为( )
A.45°
B.50°
C.60°
D.75°
7.如图,圆O是Rt△ABC的外接圆,∠ACB=90°,∠A=25°,过点C作圆O的切线,交AB的延长线于点D,则∠D的度数是( )
A.25°
B.40°
C.50°
D.65°
8.如图,P为⊙O的直径BA延长线上的一点,PC与⊙O相切,切点为C,点D是⊙上一点,连接PD.已知PC=PD=BC.下列结论:
(1)PD与⊙O相切;(2)四边形PCBD是菱形;(3)PO=AB;(4)∠PDB=120°.
其中正确的个数为( )
A.4个
B.3个
C.2个
D.1个
9.圆I是三角形ABC的内切圆,D,E,F为3个切点,若∠DEF=52°,则∠A的度数为( )
A.68°
B.52°
C.76°
D.38°
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
(9题图)
(10题图)
(11题图)
10.如图,在5×5的正方形网格中,每个小正方形的边长都为1,若将△AOB绕点O顺时针旋转90°得到△A′OB′,则A点运动的路径的长为( )
A.π
B.2π
C.4π
D.8π
11.如图,在Rt△AOB中,∠AOB=
( http: / / www.21cnjy.com )90°,OA=3,OB=2,将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE,将线段EF绕点E逆时针旋转90°后得线段ED,分别以O,E为圆心,OA、ED长为半径画弧AF和弧DF,连接AD,则图中阴影部分面积是( )
A.π
B.
C.3+π
D.8﹣π
12.一个长为4cm,宽为3cm的长方形木
( http: / / www.21cnjy.com )板在桌面上做无滑动的翻滚(顺时针方向),木板点A位置的变化为A→Al→A2,其中第二次翻滚被面上一小木块挡住,使木板与桌面成30°的角,则点A滚到A2位置时共走过的路径长为( )
A.
B.
C.
D.
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
(12题图)
(13题图)
(14题图)
13.如图,直径AB为12的半圆,绕A点逆时针旋转60°,此时点B旋转到点B′,则图中阴影部分的面积是( )
A.12π
B.24π
C.6π
D.36π
14.如图,菱形ABCD的边长为2,∠A=
( http: / / www.21cnjy.com )60°,以点B为圆心的圆与AD、DC相切,与AB、CB的延长线分别相交于点E、F,则图中阴影部分的面积为( )
A.+
B.+π
C.﹣
D.2+
15.如图,图中正方形ABCD的边长为4,则图中阴影部分的面积为( )
A.16﹣4π
B.32﹣8π
C.8π﹣16
D.无法确定
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
(15题图)
(16题图)
(17题图)
(19题图)
16.如图,在边长为2的正方形内部,以各边为直径画四个半圆,则图中阴影部分的面积是( )
A.2
B.
C.
D.1
二.填空题(共4小题)
17.如图所示,⊙O内有折线OABC,其中OA=2,AB=4,∠A=∠B=60°,则BC的长为 .
18.如图,圆心都在x轴正半轴上的半圆O1、半圆O2、…、半圆On与直线相切,设半圆O1、半圆O2、…、半圆On的半径分别是r1、r2、…、rn,则当r1=1时,r2016= .
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
(18题图)
(19题图)
19.如图,⊙I为△ABC
( http: / / www.21cnjy.com )的内切圆,点D,E分别为边AB,AC上的点,且DE为⊙I的切线,若△ABC的周长为21,BC边的长为6,△ADE的周长为 .
20.如图,半径为5的半圆的初始状态是
( http: / / www.21cnjy.com )直径平行于桌面上的直线b,然后把半圆沿直线b进行无滑动滚动,使半圆的直径与直线b重合为止,则圆心O运动路径的长度等于 .
三.解答题(共4小题)
21.如图,CD为⊙O的直径,CD⊥AB,垂足为点F,AO⊥BC,垂足为E,,
(1)求AB的长;
(2)求⊙O的半径.
( http: / / www.21cnjy.com )
22.如图,已知⊙O的直径为AB,AC⊥AB于点A,BC与⊙O相交于点D,在AC上取一点E,使得ED=EA.
(1)求证:ED是⊙O的切线;
(2)当OE=10时,求BC的长.
( http: / / www.21cnjy.com )
23.如图,Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,过点D作⊙O的切线交BC于点E.
(1)求证:点E为BC中点;
(2)若tan∠EDC=,AD=5,求DE的长.
( http: / / www.21cnjy.com )
24.如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠ACD=120°.
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为2,求图中阴影部分的面积.
( http: / / www.21cnjy.com )
青岛版九年级数学第三单元复习题参考答案
一.选择题(共16小题)
1.C.2.C.3.
C.4.
D.5.
C.6.
C.7.
B.8.A.9.
C.10.B.
11.D.12.
B.13.
B.14.A. 15.
C.16.
D.
二.填空题(共4小题)
17. 6 .18. 32015 .19. 9 .20. 5π .
三.解答题(共4小题)
21.解:(1)∵CD为⊙O的直径,CD⊥AB,∴=,AF=BF,∴∠C=∠AOD,
∵∠AOD=∠COE,∴∠C=∠COE,
∵AO⊥BC,∴∠AEC=90°,∴∠C=30°,
∵BC=2,∴BF=BC=,∴AB=2BF=2;
(2)∵AO⊥BC,BC=2,∴CE=BE=BC=,
∵∠C=30°,∴OC===2,即⊙O的半径是2.
22.(1)证明:如图,连接OD.∵AC⊥AB,∴∠BAC=90°,即∠OAE=90°.
在△AOE与△DOE中,,∴△AOE≌△DOE(SSS),
∴∠OAE=∠ODE=90°,即OD⊥ED.
又∵OD是⊙O的半径,∴ED是⊙O的切线;
(2)解:如图,∵OE=10.AB是直径,∴∠ADB=90°,即AD⊥BC.
又∵由(1)知,△AOE≌△DOE,∴∠AEO=∠DEO,
又∵AE=DE,∴OE⊥AD,∴OE∥BC,∴=,
∴BC=2OE=20,即BC的长是20.
23.解:(1)连结OD,BD,
∵AB为直径,∴∠ADB=90°,又∠ABC=90°,∴BC是⊙O切线,
∵DE是⊙O切线,∴BE=DE,∴∠EBD=∠EDB,
∵∠ADB=90°,∴∠EBD+∠C=90°,∠EDB+∠CDE=90°,∴∠C=∠EDC,∴DE=CE,
∴BE=CE,则E为BC的中点;
(2)∵∠ABC=90°,∠ADB=90°,∴∠C=∠ABD=∠EDC,sinC=,
∴cosC==,tanC==,
Rt△ABD中,DB==5×,
Rt△BDC中,BC==5××=6,
又点E为BC中点,∴DE=BC=3.
24.(1)证明:连接OC.∵AC=CD,∠ACD=120°,∴∠A=∠D=30°.
∵OA=OC,∴∠2=∠A=30°.∴∠OCD=180°﹣∠A﹣∠D﹣∠2=90°.即OC⊥CD,
∴CD是⊙O的切线.
(2)解:∵∠A=30°,∴∠1=2∠A=60°.∴S扇形BOC=.
在Rt△OCD中,∵,∴.
∴.
∴图中阴影部分的面积为:.
( http: / / www.21cnjy.com )
一.选择题(共16小题)
1.把一张圆形纸片按如图所示方式折叠两次后展开,图中的虚线表示折痕,则的度数是( )
A.120°
B.135°
C.150°
D.165°
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
(1题图)
(2题图)
(4题图)
2.如图,已知AB是⊙O的直径,弦CD⊥AB于E,连接BC,BD,AC,则下列结论中不一定正确的是( )
A.∠ACB=90°
B.DE=CE
C.OE=BE
D.∠ACE=∠ABC
3.给定下列图形可以确定一个圆的是( )
A.已知圆心
B.已知半径
C.已知直径
D.三个点
4.如图,在平面直角坐标系中,点A,B,C的坐标为(1,4),(5,4),(1,﹣2),则△ABC外接圆的圆心坐标是( )
A.(2,3)
B.(3,2)
C.(1,3)
D.(3,1)
5.如图,半径为3的⊙A经过原点O和点C(0,2),B是y轴左侧⊙A优弧上一点,则tan∠OBC为( )
A.
B.2
C.
D.
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
(5题图)
(6题图)
(7题图)
(8题图)
6.如图,四边形ABCD内接于⊙O,若四边形ABCO是平行四边形,则∠ADC的大小为( )
A.45°
B.50°
C.60°
D.75°
7.如图,圆O是Rt△ABC的外接圆,∠ACB=90°,∠A=25°,过点C作圆O的切线,交AB的延长线于点D,则∠D的度数是( )
A.25°
B.40°
C.50°
D.65°
8.如图,P为⊙O的直径BA延长线上的一点,PC与⊙O相切,切点为C,点D是⊙上一点,连接PD.已知PC=PD=BC.下列结论:
(1)PD与⊙O相切;(2)四边形PCBD是菱形;(3)PO=AB;(4)∠PDB=120°.
其中正确的个数为( )
A.4个
B.3个
C.2个
D.1个
9.圆I是三角形ABC的内切圆,D,E,F为3个切点,若∠DEF=52°,则∠A的度数为( )
A.68°
B.52°
C.76°
D.38°
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
(9题图)
(10题图)
(11题图)
10.如图,在5×5的正方形网格中,每个小正方形的边长都为1,若将△AOB绕点O顺时针旋转90°得到△A′OB′,则A点运动的路径的长为( )
A.π
B.2π
C.4π
D.8π
11.如图,在Rt△AOB中,∠AOB=
( http: / / www.21cnjy.com )90°,OA=3,OB=2,将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE,将线段EF绕点E逆时针旋转90°后得线段ED,分别以O,E为圆心,OA、ED长为半径画弧AF和弧DF,连接AD,则图中阴影部分面积是( )
A.π
B.
C.3+π
D.8﹣π
12.一个长为4cm,宽为3cm的长方形木
( http: / / www.21cnjy.com )板在桌面上做无滑动的翻滚(顺时针方向),木板点A位置的变化为A→Al→A2,其中第二次翻滚被面上一小木块挡住,使木板与桌面成30°的角,则点A滚到A2位置时共走过的路径长为( )
A.
B.
C.
D.
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
(12题图)
(13题图)
(14题图)
13.如图,直径AB为12的半圆,绕A点逆时针旋转60°,此时点B旋转到点B′,则图中阴影部分的面积是( )
A.12π
B.24π
C.6π
D.36π
14.如图,菱形ABCD的边长为2,∠A=
( http: / / www.21cnjy.com )60°,以点B为圆心的圆与AD、DC相切,与AB、CB的延长线分别相交于点E、F,则图中阴影部分的面积为( )
A.+
B.+π
C.﹣
D.2+
15.如图,图中正方形ABCD的边长为4,则图中阴影部分的面积为( )
A.16﹣4π
B.32﹣8π
C.8π﹣16
D.无法确定
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
(15题图)
(16题图)
(17题图)
(19题图)
16.如图,在边长为2的正方形内部,以各边为直径画四个半圆,则图中阴影部分的面积是( )
A.2
B.
C.
D.1
二.填空题(共4小题)
17.如图所示,⊙O内有折线OABC,其中OA=2,AB=4,∠A=∠B=60°,则BC的长为 .
18.如图,圆心都在x轴正半轴上的半圆O1、半圆O2、…、半圆On与直线相切,设半圆O1、半圆O2、…、半圆On的半径分别是r1、r2、…、rn,则当r1=1时,r2016= .
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
(18题图)
(19题图)
19.如图,⊙I为△ABC
( http: / / www.21cnjy.com )的内切圆,点D,E分别为边AB,AC上的点,且DE为⊙I的切线,若△ABC的周长为21,BC边的长为6,△ADE的周长为 .
20.如图,半径为5的半圆的初始状态是
( http: / / www.21cnjy.com )直径平行于桌面上的直线b,然后把半圆沿直线b进行无滑动滚动,使半圆的直径与直线b重合为止,则圆心O运动路径的长度等于 .
三.解答题(共4小题)
21.如图,CD为⊙O的直径,CD⊥AB,垂足为点F,AO⊥BC,垂足为E,,
(1)求AB的长;
(2)求⊙O的半径.
( http: / / www.21cnjy.com )
22.如图,已知⊙O的直径为AB,AC⊥AB于点A,BC与⊙O相交于点D,在AC上取一点E,使得ED=EA.
(1)求证:ED是⊙O的切线;
(2)当OE=10时,求BC的长.
( http: / / www.21cnjy.com )
23.如图,Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,过点D作⊙O的切线交BC于点E.
(1)求证:点E为BC中点;
(2)若tan∠EDC=,AD=5,求DE的长.
( http: / / www.21cnjy.com )
24.如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠ACD=120°.
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为2,求图中阴影部分的面积.
( http: / / www.21cnjy.com )
青岛版九年级数学第三单元复习题参考答案
一.选择题(共16小题)
1.C.2.C.3.
C.4.
D.5.
C.6.
C.7.
B.8.A.9.
C.10.B.
11.D.12.
B.13.
B.14.A. 15.
C.16.
D.
二.填空题(共4小题)
17. 6 .18. 32015 .19. 9 .20. 5π .
三.解答题(共4小题)
21.解:(1)∵CD为⊙O的直径,CD⊥AB,∴=,AF=BF,∴∠C=∠AOD,
∵∠AOD=∠COE,∴∠C=∠COE,
∵AO⊥BC,∴∠AEC=90°,∴∠C=30°,
∵BC=2,∴BF=BC=,∴AB=2BF=2;
(2)∵AO⊥BC,BC=2,∴CE=BE=BC=,
∵∠C=30°,∴OC===2,即⊙O的半径是2.
22.(1)证明:如图,连接OD.∵AC⊥AB,∴∠BAC=90°,即∠OAE=90°.
在△AOE与△DOE中,,∴△AOE≌△DOE(SSS),
∴∠OAE=∠ODE=90°,即OD⊥ED.
又∵OD是⊙O的半径,∴ED是⊙O的切线;
(2)解:如图,∵OE=10.AB是直径,∴∠ADB=90°,即AD⊥BC.
又∵由(1)知,△AOE≌△DOE,∴∠AEO=∠DEO,
又∵AE=DE,∴OE⊥AD,∴OE∥BC,∴=,
∴BC=2OE=20,即BC的长是20.
23.解:(1)连结OD,BD,
∵AB为直径,∴∠ADB=90°,又∠ABC=90°,∴BC是⊙O切线,
∵DE是⊙O切线,∴BE=DE,∴∠EBD=∠EDB,
∵∠ADB=90°,∴∠EBD+∠C=90°,∠EDB+∠CDE=90°,∴∠C=∠EDC,∴DE=CE,
∴BE=CE,则E为BC的中点;
(2)∵∠ABC=90°,∠ADB=90°,∴∠C=∠ABD=∠EDC,sinC=,
∴cosC==,tanC==,
Rt△ABD中,DB==5×,
Rt△BDC中,BC==5××=6,
又点E为BC中点,∴DE=BC=3.
24.(1)证明:连接OC.∵AC=CD,∠ACD=120°,∴∠A=∠D=30°.
∵OA=OC,∴∠2=∠A=30°.∴∠OCD=180°﹣∠A﹣∠D﹣∠2=90°.即OC⊥CD,
∴CD是⊙O的切线.
(2)解:∵∠A=30°,∴∠1=2∠A=60°.∴S扇形BOC=.
在Rt△OCD中,∵,∴.
∴.
∴图中阴影部分的面积为:.
( http: / / www.21cnjy.com )
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
