湘教版八年级数学(上)第二章《三角形》提升卷
文档属性
| 名称 | 湘教版八年级数学(上)第二章《三角形》提升卷 | 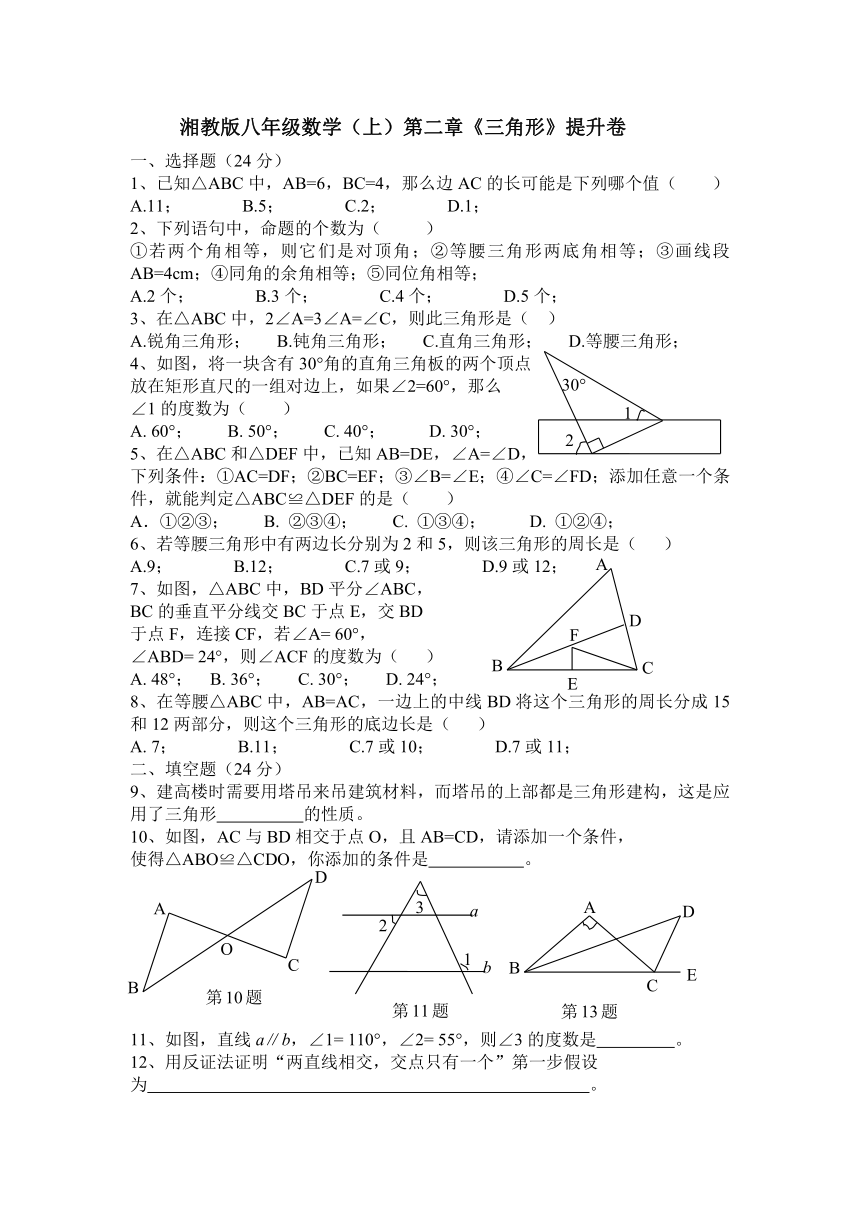 | |
| 格式 | zip | ||
| 文件大小 | 25.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-10-31 13:51:20 | ||
图片预览

文档简介
湘教版八年级数学(上)第二章《三角形》提升卷
一、选择题(24分)
1、已知△ABC中,AB=6,BC=4,那么边AC的长可能是下列哪个值(
)
A.11;
B.5;
C.2;
D.1;
2、下列语句中,命题的个数为(
)
①若两个角相等,则它们是对顶角;②等腰三角形两底角相等;③画线段AB=4cm;④同角的余角相等;⑤同位角相等;
A.2个;
B.3个;
C.4个;
D.5个;
3、在△ABC中,2∠A=3∠A=∠C,则此三角形是(
)
A.锐角三角形;
B.钝角三角形;
C.直角三角形;
D.等腰三角形;
4、如图,将一块含有30°角的直角三角板的两个顶点
放在矩形直尺的一组对边上,如果∠2=60°,那么
∠1的度数为(
)
A.
60°;
B.
50°;
C.
40°;
D.
30°;
5、在△ABC和△DEF中,已知AB=DE,∠A=∠D,
下列条件:①AC=DF;②BC=EF;③∠B=∠E;④∠C=∠FD;添加任意一个条件,就能判定△ABC≌△DEF的是(
)
A.①②③;
B.
②③④;
C.
①③④;
D.
①②④;
6、若等腰三角形中有两边长分别为2和5,则该三角形的周长是(
)
A.9;
B.12;
C.7或9;
D.9或12;
7、如图,△ABC中,BD平分∠ABC,
BC的垂直平分线交BC于点E,交BD
于点F,连接CF,若∠A=
60°,
∠ABD=
24°,则∠ACF的度数为(
)
A.
48°;
B.
36°;
C.
30°;
D.
24°;
8、在等腰△ABC中,AB=AC,一边上的中线BD将这个三角形的周长分成15和12两部分,则这个三角形的底边长是(
)
A.
7;
B.11;
C.7或10;
D.7或11;
二、填空题(24分)
9、建高楼时需要用塔吊来吊建筑材料,而塔吊的上部都是三角形建构,这是应用了三角形
的性质。
10、如图,AC与BD相交于点O,且AB=CD,请添加一个条件,
使得△ABO≌△CDO,你添加的条件是
。
11、如图,直线a∥b,∠1=
110°,∠2=
55°,则∠3的度数是
。
12、用反证法证明“两直线相交,交点只有一个”第一步假设
为
。
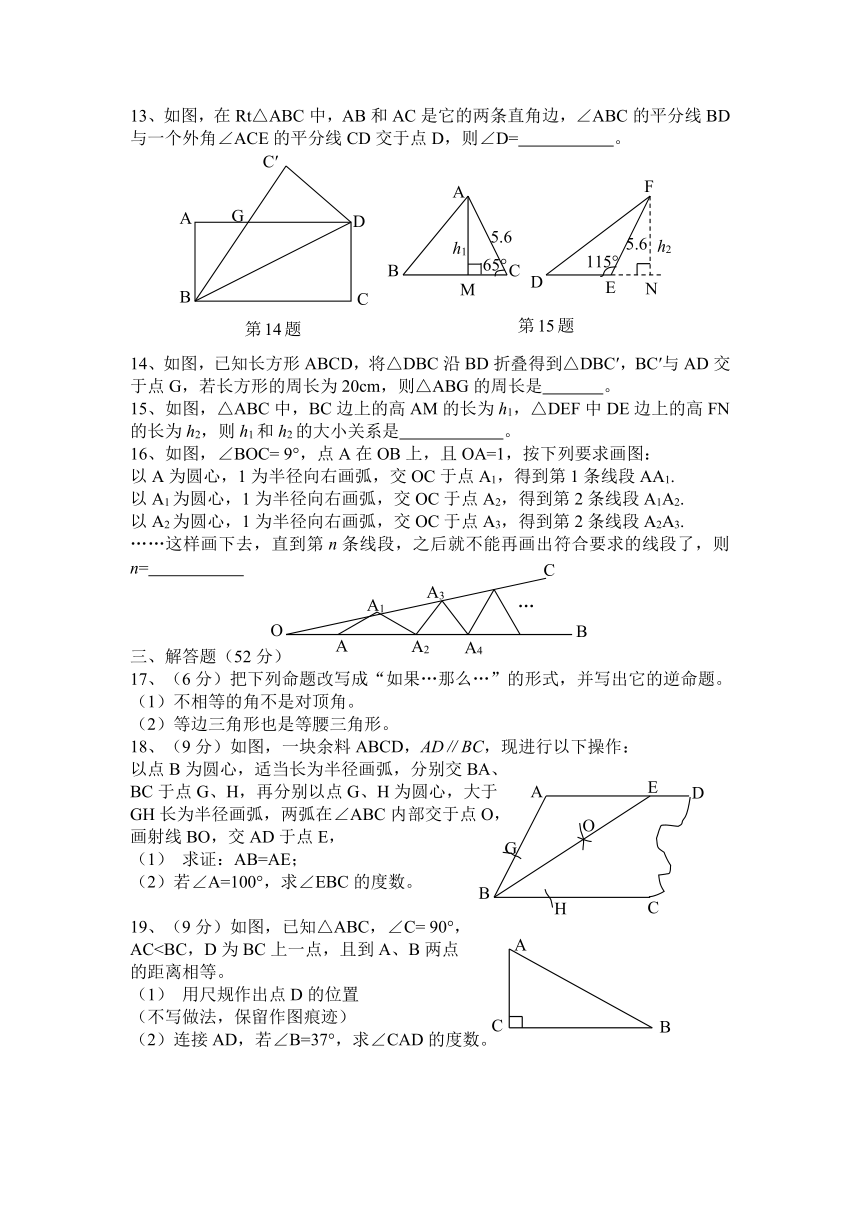
13、如图,在Rt△ABC中,AB和AC是它的两条直角边,∠ABC的平分线BD与一个外角∠ACE的平分线CD交于点D,则∠D=
。
14、如图,已知长方形ABCD,将△DBC沿BD折叠得到△DBC′,BC′与AD交于点G,若长方形的周长为20cm,则△ABG的周长是
。
15、如图,△ABC中,BC边上的高AM的长为h1,△DEF中DE边上的高FN的长为h2,则h1和h2的大小关系是
。
16、如图,∠BOC=
9°,点A在OB上,且OA=1,按下列要求画图:
以A为圆心,1为半径向右画弧,交OC于点A1,得到第1条线段AA1.
以A1为圆心,1为半径向右画弧,交OC于点A2,得到第2条线段A1A2.
以A2为圆心,1为半径向右画弧,交OC于点A3,得到第2条线段A2A3.
……这样画下去,直到第n条线段,之后就不能再画出符合要求的线段了,则n=
三、解答题(52分)
17、(6分)把下列命题改写成“如果…那么…”的形式,并写出它的逆命题。
(1)不相等的角不是对顶角。
(2)等边三角形也是等腰三角形。
18、(9分)如图,一块余料ABCD,AD∥BC,现进行以下操作:
以点B为圆心,适当长为半径画弧,分别交BA、
BC于点G、H,再分别以点G、H为圆心,大于
GH长为半径画弧,两弧在∠ABC内部交于点O,
画射线BO,交AD于点E,
求证:AB=AE;
(2)若∠A=100°,求∠EBC的度数。
19、(9分)如图,已知△ABC,∠C=
90°,
AC的距离相等。
用尺规作出点D的位置
(不写做法,保留作图痕迹)
(2)连接AD,若∠B=37°,求∠CAD的度数。
20、(9分)如图,在等边△ABC中,∠ABC、∠ACB的角平分线相交于点O,
作BO、CO的垂直平分线,分别交BC于E、F,
于是,小明说:“点E、F是BC的三等分点”。
你同意小明的说法吗?说明理由。
21、(9分)已知△ABC,AB=AC,将△ABC沿BC方向平移得到△DEF,
如图,连接BD、AF,则BD
AF。(填“>”“=”“<”)
并说明理由。
22、(10分)如图,已知AD、AE分别是△ABC的高和中线,AB=6cm,AC=8cm,BC=10cm,∠CAB=
90°,试求:
(1)AD的长;
(2)△ABE的面积;
(3)△ACE和△ABE的周长的差。
参考答案:
一、1、B;2、C;3、C;4、D;5、C;6、B;7、A;8、D;
二、9、稳定性;10、∠A=∠C或
AB∥CD或∠B=∠D;11、55°;
12、两条直线相交交点不止一个;13、45°;14、10cm;15、h1=h2;16、9;
三、17、(1)如果两个角不相等,那么它们不是对顶角。
逆命题:不是对顶角的两个角不相等。
(2)如果一个三角形是等边三角形,那么它也是等腰三角形。
逆命题:等腰三角形也是等边三角形。
18、证明:(1)∵AD∥BC,∴∠AEB=∠EBC
由BE是∠ABC的角平分线,∴∠EBC=∠ABE
∴∠AEB=∠ABE,∴AB=AE;
(2)由∠A=100°,∠AEB=∠ABE,得:∠AEB=∠ABE=40°,
∴∠EBC=∠ABE=40°.
19、(1)作AB的垂直平分线,与BC的交点即为D。
(2)∵在Rt△ABC中,∠B=37°,∴∠CAB=53°,
又∵AD=BD,∴∠DAB=∠B=37°,∴∠CAD=53°-37°=16°.
20、同意小明的说法。
理由:连接OE、OF,由题意知,BE=OE,CF=OF,∠OCF=∠OBC=30°,
∴∠BOE=∠OBC=30°,∠COF=∠OCB=30°,∠BOC=120°,
∴∠EOF=60°,∠OEF=60°,∠OFE=60°,
∴△OEF是等边三角形。∴OE=OF=EF=BE=CF,
即,点E、F是BC的三等分点。
21、填空“=”
理由:由平移可知:△ABC≌△DEF,∴AB=DE=AC=DF
∴∠ABF=∠DFB,BF=FB,∴△ABF≌△DFB(SAS)
∴BD=AF.
22、解:(1)
,∴AD=4.8
(2)∵AE是△ABC中线,∴
(3)∵AE是△ABC中线,∴BE=CE
∴=AC+CE+AE-(AB+BE+AE)=AC-AB=8-6=2(cm)
30°
1
2
A
B
C
D
E
F
A
B
C
D
O
第10题
A
B
C
D
E
第13题
a
b
1
2
3
第11题
A
B
C
D
G
C′
第14题
第15题
A
B
C
M
h2
h1
115°
65°
5.6
5.6
D
E
F
N
B
A
…
O
A1
A2
A3
A4
C
A
B
C
D
G
H
E
O
A
B
C
A
B
C
E
F
O
A
B
C
D
E
F
A
B
C
D
E
一、选择题(24分)
1、已知△ABC中,AB=6,BC=4,那么边AC的长可能是下列哪个值(
)
A.11;
B.5;
C.2;
D.1;
2、下列语句中,命题的个数为(
)
①若两个角相等,则它们是对顶角;②等腰三角形两底角相等;③画线段AB=4cm;④同角的余角相等;⑤同位角相等;
A.2个;
B.3个;
C.4个;
D.5个;
3、在△ABC中,2∠A=3∠A=∠C,则此三角形是(
)
A.锐角三角形;
B.钝角三角形;
C.直角三角形;
D.等腰三角形;
4、如图,将一块含有30°角的直角三角板的两个顶点
放在矩形直尺的一组对边上,如果∠2=60°,那么
∠1的度数为(
)
A.
60°;
B.
50°;
C.
40°;
D.
30°;
5、在△ABC和△DEF中,已知AB=DE,∠A=∠D,
下列条件:①AC=DF;②BC=EF;③∠B=∠E;④∠C=∠FD;添加任意一个条件,就能判定△ABC≌△DEF的是(
)
A.①②③;
B.
②③④;
C.
①③④;
D.
①②④;
6、若等腰三角形中有两边长分别为2和5,则该三角形的周长是(
)
A.9;
B.12;
C.7或9;
D.9或12;
7、如图,△ABC中,BD平分∠ABC,
BC的垂直平分线交BC于点E,交BD
于点F,连接CF,若∠A=
60°,
∠ABD=
24°,则∠ACF的度数为(
)
A.
48°;
B.
36°;
C.
30°;
D.
24°;
8、在等腰△ABC中,AB=AC,一边上的中线BD将这个三角形的周长分成15和12两部分,则这个三角形的底边长是(
)
A.
7;
B.11;
C.7或10;
D.7或11;
二、填空题(24分)
9、建高楼时需要用塔吊来吊建筑材料,而塔吊的上部都是三角形建构,这是应用了三角形
的性质。
10、如图,AC与BD相交于点O,且AB=CD,请添加一个条件,
使得△ABO≌△CDO,你添加的条件是
。
11、如图,直线a∥b,∠1=
110°,∠2=
55°,则∠3的度数是
。
12、用反证法证明“两直线相交,交点只有一个”第一步假设
为
。
13、如图,在Rt△ABC中,AB和AC是它的两条直角边,∠ABC的平分线BD与一个外角∠ACE的平分线CD交于点D,则∠D=
。
14、如图,已知长方形ABCD,将△DBC沿BD折叠得到△DBC′,BC′与AD交于点G,若长方形的周长为20cm,则△ABG的周长是
。
15、如图,△ABC中,BC边上的高AM的长为h1,△DEF中DE边上的高FN的长为h2,则h1和h2的大小关系是
。
16、如图,∠BOC=
9°,点A在OB上,且OA=1,按下列要求画图:
以A为圆心,1为半径向右画弧,交OC于点A1,得到第1条线段AA1.
以A1为圆心,1为半径向右画弧,交OC于点A2,得到第2条线段A1A2.
以A2为圆心,1为半径向右画弧,交OC于点A3,得到第2条线段A2A3.
……这样画下去,直到第n条线段,之后就不能再画出符合要求的线段了,则n=
三、解答题(52分)
17、(6分)把下列命题改写成“如果…那么…”的形式,并写出它的逆命题。
(1)不相等的角不是对顶角。
(2)等边三角形也是等腰三角形。
18、(9分)如图,一块余料ABCD,AD∥BC,现进行以下操作:
以点B为圆心,适当长为半径画弧,分别交BA、
BC于点G、H,再分别以点G、H为圆心,大于
GH长为半径画弧,两弧在∠ABC内部交于点O,
画射线BO,交AD于点E,
求证:AB=AE;
(2)若∠A=100°,求∠EBC的度数。
19、(9分)如图,已知△ABC,∠C=
90°,
AC
用尺规作出点D的位置
(不写做法,保留作图痕迹)
(2)连接AD,若∠B=37°,求∠CAD的度数。
20、(9分)如图,在等边△ABC中,∠ABC、∠ACB的角平分线相交于点O,
作BO、CO的垂直平分线,分别交BC于E、F,
于是,小明说:“点E、F是BC的三等分点”。
你同意小明的说法吗?说明理由。
21、(9分)已知△ABC,AB=AC,将△ABC沿BC方向平移得到△DEF,
如图,连接BD、AF,则BD
AF。(填“>”“=”“<”)
并说明理由。
22、(10分)如图,已知AD、AE分别是△ABC的高和中线,AB=6cm,AC=8cm,BC=10cm,∠CAB=
90°,试求:
(1)AD的长;
(2)△ABE的面积;
(3)△ACE和△ABE的周长的差。
参考答案:
一、1、B;2、C;3、C;4、D;5、C;6、B;7、A;8、D;
二、9、稳定性;10、∠A=∠C或
AB∥CD或∠B=∠D;11、55°;
12、两条直线相交交点不止一个;13、45°;14、10cm;15、h1=h2;16、9;
三、17、(1)如果两个角不相等,那么它们不是对顶角。
逆命题:不是对顶角的两个角不相等。
(2)如果一个三角形是等边三角形,那么它也是等腰三角形。
逆命题:等腰三角形也是等边三角形。
18、证明:(1)∵AD∥BC,∴∠AEB=∠EBC
由BE是∠ABC的角平分线,∴∠EBC=∠ABE
∴∠AEB=∠ABE,∴AB=AE;
(2)由∠A=100°,∠AEB=∠ABE,得:∠AEB=∠ABE=40°,
∴∠EBC=∠ABE=40°.
19、(1)作AB的垂直平分线,与BC的交点即为D。
(2)∵在Rt△ABC中,∠B=37°,∴∠CAB=53°,
又∵AD=BD,∴∠DAB=∠B=37°,∴∠CAD=53°-37°=16°.
20、同意小明的说法。
理由:连接OE、OF,由题意知,BE=OE,CF=OF,∠OCF=∠OBC=30°,
∴∠BOE=∠OBC=30°,∠COF=∠OCB=30°,∠BOC=120°,
∴∠EOF=60°,∠OEF=60°,∠OFE=60°,
∴△OEF是等边三角形。∴OE=OF=EF=BE=CF,
即,点E、F是BC的三等分点。
21、填空“=”
理由:由平移可知:△ABC≌△DEF,∴AB=DE=AC=DF
∴∠ABF=∠DFB,BF=FB,∴△ABF≌△DFB(SAS)
∴BD=AF.
22、解:(1)
,∴AD=4.8
(2)∵AE是△ABC中线,∴
(3)∵AE是△ABC中线,∴BE=CE
∴=AC+CE+AE-(AB+BE+AE)=AC-AB=8-6=2(cm)
30°
1
2
A
B
C
D
E
F
A
B
C
D
O
第10题
A
B
C
D
E
第13题
a
b
1
2
3
第11题
A
B
C
D
G
C′
第14题
第15题
A
B
C
M
h2
h1
115°
65°
5.6
5.6
D
E
F
N
B
A
…
O
A1
A2
A3
A4
C
A
B
C
D
G
H
E
O
A
B
C
A
B
C
E
F
O
A
B
C
D
E
F
A
B
C
D
E
同课章节目录
