24.1.4圆周角 课件

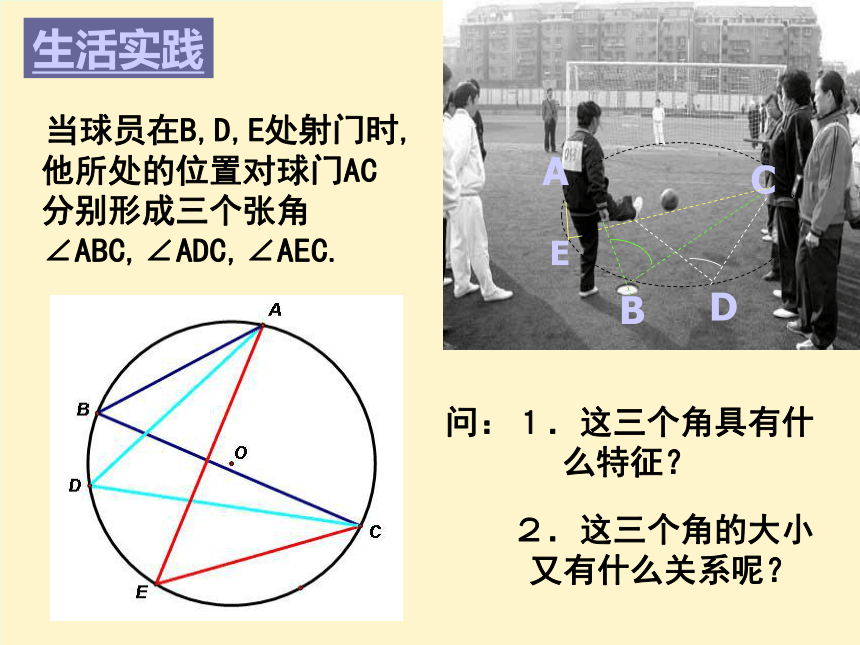
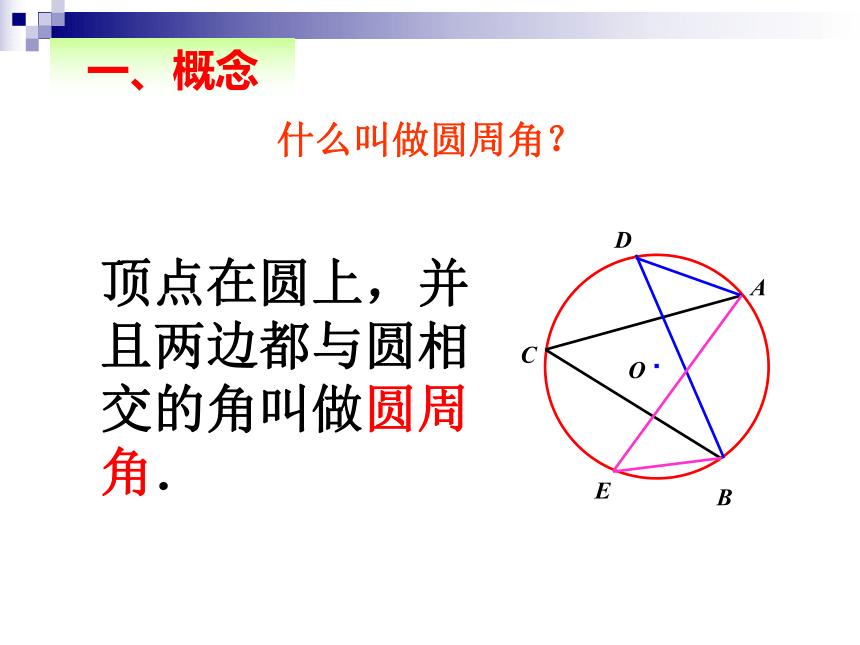
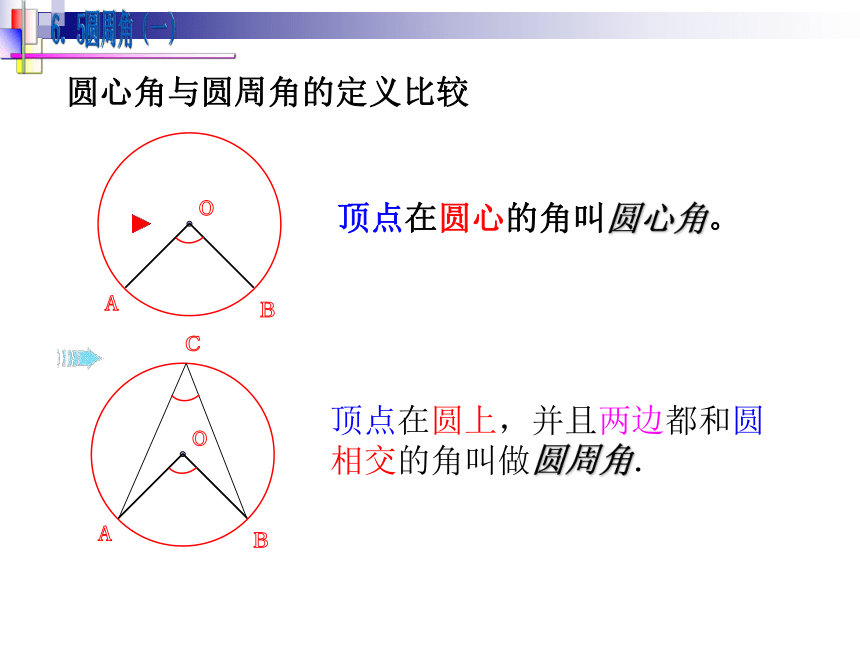
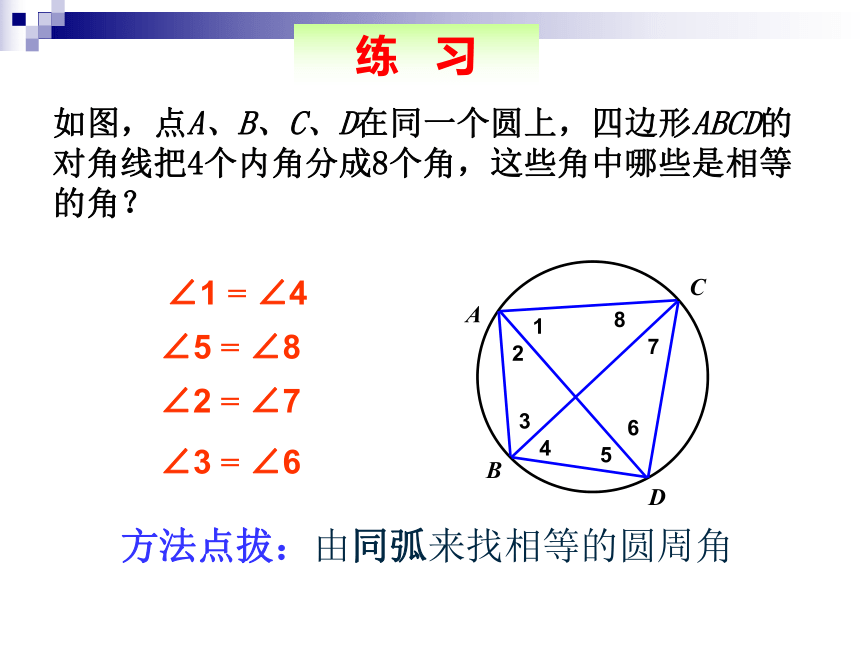
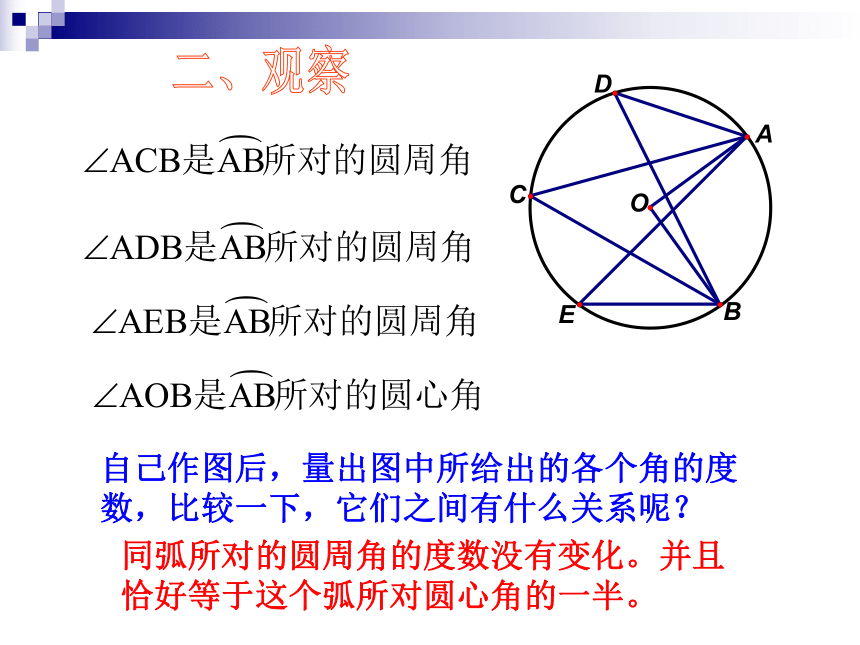
课件26张PPT。24.1.4 圆周角一. 复习引入:1.圆心角的定义?在同圆（或等圆）中，如果圆心角、弧、弦有一组量相等，那么它们所对应的其余两个量都分别相等。答:顶点在圆心的角叫圆心角2.上节课我们学习了一个反映圆心角、弧、弦三个量之间关系的一个结论，这个结论是什么？ 当球员在B,D,E处射门时,他所处的位置对球门AC分别形成三个张角∠ABC,∠ADC,∠AEC.问：１．这三个角具有什么特征？２．这三个角的大小又有什么关系呢？　生活实践顶点在圆上，并且两边都与圆相交的角叫做圆周角．什么叫做圆周角？·ABCO一、概念圆心角与圆周角的定义比较顶点在圆心的角叫圆心角。顶点在圆上，并且两边都和圆相交的角叫做圆周角． 练习：判断下列各图中，哪些是圆周角，为什么？ oABoABoABoABoABoABoABoABCCCCCCCC图1图2图3图4图5图6图7图8图9自己作图后，量出图中所给出的各个角的度数，比较一下，它们之间有什么关系呢？二、观察如图，点A、B、C、D在同一个圆上，四边形ABCD的对角线把4个内角分成8个角，这些角中哪些是相等的角？ABCD12345678∠1 = ∠4∠5 = ∠8∠2 = ∠7∠3 = ∠6练 习方法点拔：由同弧来找相等的圆周角自己作图后，量出图中所给出的各个角的度数，比较一下，它们之间有什么关系呢？二、观察同弧所对的圆周角的度数没有变化。并且恰好等于这个弧所对圆心角的一半。为了进一步探究上面的发现，如图在⊙O任取一个圆周角∠BAC，将圆对折，使折痕经过圆心O和∠BAC的顶点A．由于点A的位置的取法可能不同，这时折痕可能会:
（1）在圆周角的一条边上；
（2）在圆周角的内部：
（3）在圆周角的外部。三、同弧所对圆周角与圆心角的关系教师提示:注意圆心与圆周角的位置关系.（1）在圆周角的一条边上；·COAB三、同弧所对圆周角与圆心角的关系∵OA=OC，∴∠A=∠C．又∵∠BOC=∠A+∠C∴∠BOC=2∠A圆心O在∠BAC的一条边上，直径AB，有（2）在圆周角的内部．圆心O在∠BAC的内部，作直径AD，利用(1)的结果，有·COABD（3）在圆周角的外部．圆心O在∠BAC的外部，作直径AD，利用(1)的结果，有·COABD动手实践：１．如图(１)：AB是直径,你能确定∠C的 度数吗?
２．如图(2),在⊙O中,∠B,∠D,∠E的大小 有什么关系? 为什么?
·ABC1OC2C3四、定理·ABCO在同圆或等圆中，如果两个圆周角相等，它们所对弧一定相等吗？为什么？ 在同圆或等圆中，如果两个圆周角相等，它们所对弧一定相等． 因为，在同圆或等圆中，
如果圆周角相等，那么它所
对的圆心角也相等，因此它
所对的弧也相等．·CBOAFGE（（五、练一练1、如图，在⊙O中，∠ABC=50°，
则∠AOC等于（ ）
A、50°； B、80°；
C、90°； D、100°D2、如图，△ABC是等边三角形，
动点P在圆周的劣弧AB上，且不
与A、B重合，则∠BPC等于（ ）
A、30°； B、60°；
C、90°； D、45°B练一练3、如图，∠A=50°， ∠ABC=60 °
BD是⊙O的直径，则∠AEB等于（ ）
A、70°； B、110°；
C、90°； D、120°B4、如图，△ABC的顶点A、B、C
都在⊙O上，∠C＝30 °，AB＝2，
则⊙O的半径是 。解：连接OA、OB∵∠C=30 ° ，∴∠AOB=60 °又∵OA=OB ，∴△AOB是等边三角形∴OA=OB=AB=2，即半径为2。2六、圆与多边形如果一个多边形的所有顶点都在同一个圆上，这个多边形叫做圆内接多边形。这个圆叫做这个多边形的外接圆。ADCBO四边形ABCD是⊙O的内接四边形， ⊙O是四边形ABCD的外接圆。六、圆与多边形利用圆周角定理，我们得到关于圆内接四边形的一个性质：圆内接四边形的对角互补。ADCBO你能证明出这个性质吗？BCD1.求圆Ｏ中角X的度数?练 习2.如图，圆心角∠AOB=100°,则∠ACB=__。3.已知⊙O中弦AB的等于半径，求弦AB所对的圆心角和圆周角的度数。 圆心角为60°圆周角为 30 °或 150 °120°35°130°例 如图，⊙O直径AB为10cm，弦AC为6cm，∠ACB的平分线交⊙O于D，求BC、AD、BD的长．又在Rt△ABD中，AD2+BD2=AB2，解：∵AB是直径，∴ ∠ACB= ∠ADB=90°．在Rt△ABC中，∵CD平分∠ACB，∴AD=BD.七、例题3.求证：如果三角形一边上的中线等于这边的一半，那么这个三角形是直角三角形（提示：作出以这条边为直径的圆.）·ABCO求证： △ABC 为直角三角形.证明：以AB为直径作⊙O，∵AO=BO， ∴AO=BO=CO.∴点C在⊙O上.又∵AB为直径,∴ △ABC 为直角三角形.*练习能力提升　1、在⊙O中，∠CBD=30° ,∠BDC=20°,求∠A2.如图 AB是⊙O的直径, C ,D是圆上的两点,若∠ABD=40°,则∠BCD=＿＿＿＿＿.40°　3.如图，在⊙O中，AB为直径，CB = CF,弦CG⊥AB，交AB于D，交BF于E.求证：BE=EC
⌒⌒50°50°6.在⊙O中,一条弧所对的圆心角和圆周角分别为(2x+100)°和(5x-30)°,则x=_ _；20°25°5题图350700∠BOC =140° 7.如图：OA、OB、OC都是⊙O的半径 ，　　且∠AOB=2∠BOC.
求证：∠ACB=2∠BAC.1.圆周角定义:顶点在圆上,并且两边都和圆相交的角叫圆周角.3.在同圆(或等圆)中，同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半；相等的圆周角所对的弧相等。2.半圆或直径所对的圆周角都相等，都等于90°
90°的圆周角所对的弦是圆的直径小结:4. 圆内接多边形与多边形的外接圆。5. 圆内接四边形的性质：圆内接四边形的对角互补。