第十三章整式的乘法---两数和的平方
文档属性
| 名称 | 第十三章整式的乘法---两数和的平方 |

|
|
| 格式 | rar | ||
| 文件大小 | 528.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-05-17 00:00:00 | ||
图片预览







文档简介
课件21张PPT。13.3 完全平方公式 有同学说:
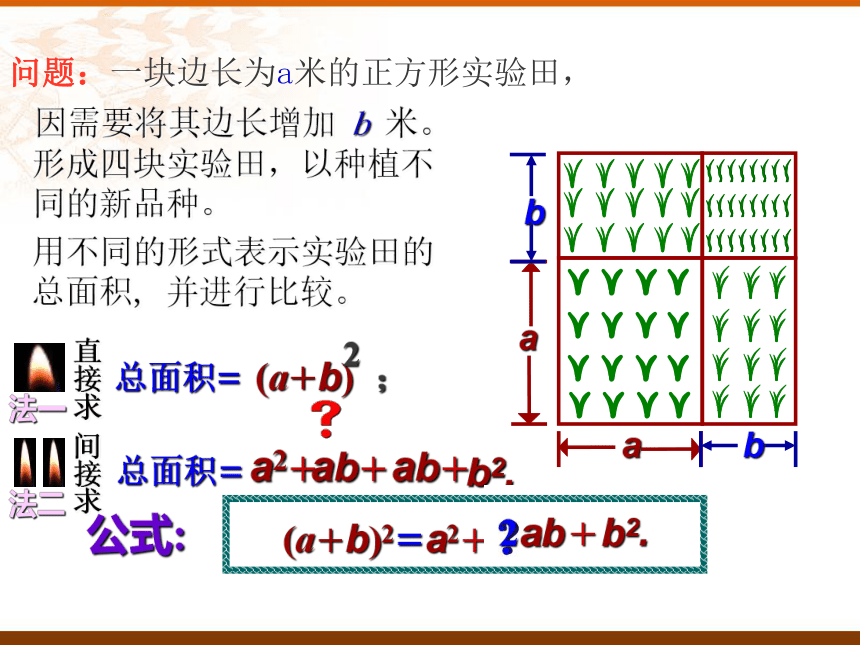
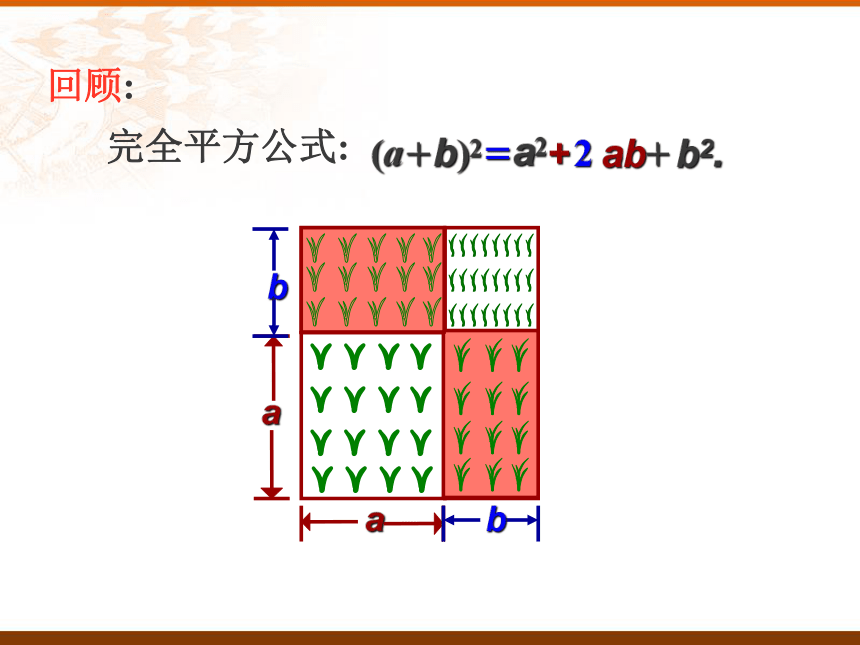
你认为对吗?如果对,请说明;如果不对,请举出反例。对吗?假设:a=3 ,b=2分别代入,得左边=右边=因为,左边≠右边答:不对。所以,问题:?问题:我们能用几何图形解释公式:问题:一块边长为a米的正方形实验田, 因需要将其边长增加 b 米。形成四块实验田,以种植不同的新品种。用不同的形式表示实验田的总面积, 并进行比较。 (a+b) ;2a2+ab+ab+b2.(a+b)2=a2+ab+b2.2(a+b)2=a2+ ab+b2.2完全平方公式:回顾:例1 利用完全平方公式计算:
; (2) ; (3) ;口诀: 两数和的平方等于前一个数的平方, 加上2倍的前后两个数的积,加上后一个数的平方.(简记为:前平方,后平方,前后两倍中间放)解: (1)例题例1 利用完全平方公式计算:
; (2) ; (3) ; 解(1)(2)(3)练一练1、填空:⑴ ⑵ ⑶2、用完全平方公式计算:⑴ ⑵ ⑶aa3xx32y2y2x2x5y5y由上述结论可得:结论完全平方公式例题例1 利用完全平方公式计算:
; (2) ; 解(1)(2)练一练 用完全平方公式计算:⑴ ⑵ ⑶已知: ①, ②;
求ab的值。公式拓展:解法一:(作差法)① — ② 得:已知: ,
求ab的值。公式拓展:解法二:分别代入,得:( ) 2ab(凑平方法)1、已知: ,
求ab的值。练一练:2、已知:
求a和b的值。小结1、完全平方公式2、运算口诀: 两数和(差)的平方等于前一个数的平方, 加上(或减去)2倍的前一个数后一个数,加上后一个数的平方.
公式拓展:运用完全平方公式计算:⑴⑵解:⑴⑵练一练:运用完全平方公式计算:⑴⑵公式拓展:用几何图形的方法验证公式:由上述结论可得:几何解释
你认为对吗?如果对,请说明;如果不对,请举出反例。对吗?假设:a=3 ,b=2分别代入,得左边=右边=因为,左边≠右边答:不对。所以,问题:?问题:我们能用几何图形解释公式:问题:一块边长为a米的正方形实验田, 因需要将其边长增加 b 米。形成四块实验田,以种植不同的新品种。用不同的形式表示实验田的总面积, 并进行比较。 (a+b) ;2a2+ab+ab+b2.(a+b)2=a2+ab+b2.2(a+b)2=a2+ ab+b2.2完全平方公式:回顾:例1 利用完全平方公式计算:
; (2) ; (3) ;口诀: 两数和的平方等于前一个数的平方, 加上2倍的前后两个数的积,加上后一个数的平方.(简记为:前平方,后平方,前后两倍中间放)解: (1)例题例1 利用完全平方公式计算:
; (2) ; (3) ; 解(1)(2)(3)练一练1、填空:⑴ ⑵ ⑶2、用完全平方公式计算:⑴ ⑵ ⑶aa3xx32y2y2x2x5y5y由上述结论可得:结论完全平方公式例题例1 利用完全平方公式计算:
; (2) ; 解(1)(2)练一练 用完全平方公式计算:⑴ ⑵ ⑶已知: ①, ②;
求ab的值。公式拓展:解法一:(作差法)① — ② 得:已知: ,
求ab的值。公式拓展:解法二:分别代入,得:( ) 2ab(凑平方法)1、已知: ,
求ab的值。练一练:2、已知:
求a和b的值。小结1、完全平方公式2、运算口诀: 两数和(差)的平方等于前一个数的平方, 加上(或减去)2倍的前一个数后一个数,加上后一个数的平方.
公式拓展:运用完全平方公式计算:⑴⑵解:⑴⑵练一练:运用完全平方公式计算:⑴⑵公式拓展:用几何图形的方法验证公式:由上述结论可得:几何解释
