23.3.3相似三角形的性质ppt课件
文档属性
| 名称 | 23.3.3相似三角形的性质ppt课件 |
|
|
| 格式 | zip | ||
| 文件大小 | 597.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-11-02 18:36:21 | ||
图片预览






文档简介
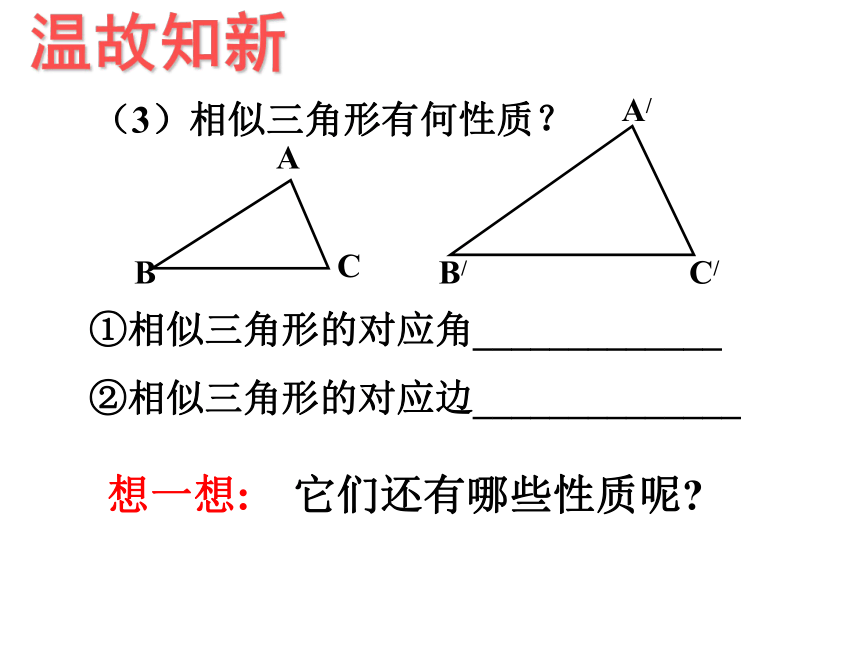
课件27张PPT。如图,一条河的两岸有一段是平行的,在河的两岸边每隔5米有一棵树,在北岸边每
隔60米有一根电线杆.小丽站在离南岸边15米的点P处看北岸,发现北岸相邻的两根
电线杆恰好被南岸的两棵树遮住,并且在这两棵树之间还有三棵树,则河宽为___米.引入:_相似三角形的性质学习目标1.掌握相似三角形的性质定理的内容及证明,进一步理解相似三角形的概念.
2.能运用相似三角形的性质定理来解决有关问题.
3.通过由特殊情况猜想到一般情况,渗透由特殊到一般的数学思想,感受数学的和谐美,并进一步养成严谨科学的学习品质.(1)什么叫相似三角形?
对应角相等、对应边成比例的三角形,叫做相似三角形.(2)如何判定两个三角形相似?①定义;
②预备定理(平行);
③两个角对应相等;两个三角形相似
④两边对应成比例,且夹角相等两个三角形相似
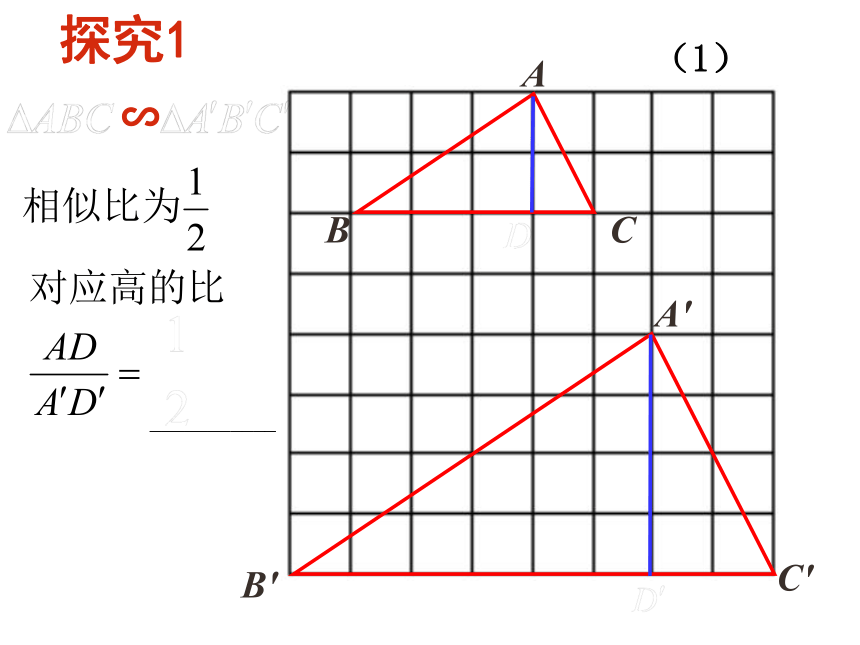
⑤三边对应成比例两个三角形相似;知识准备:ABCA/B/C/ ①相似三角形的对应角_____________
②相似三角形的对应边______________想一想: 它们还有哪些性质呢?温故知新(3)相似三角形有何性质?(1)一个三角形有三条重要线段:
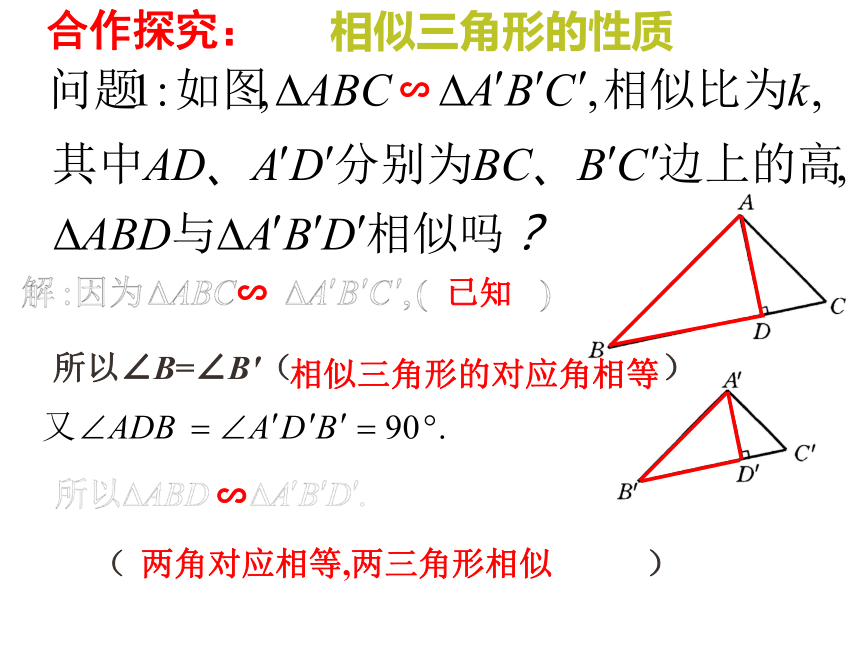
________________(2)如果两个三角形全等,那么这些对应线段有什么关系?如果两个三角形相似,那么这些对应线段又有什么关系呢?提出问题:高、中线、角平分线(1)探究1∽可得: 观察这些数据,你会有怎样的猜想呢?合作探究:两角对应相等,两三角形相似∽已知所以∠B=∠B′( )相似三角形的对应角相等 ( )相似三角形的性质合作探究:∽所以(相似三角形的对应边成比例)∽相似三角形的性质结论:相似三角形对应高的比等于相似比.探究21231∶ 2当相似比=k时,面积比等于什么? (1)(2)(3)(1)与(2)的相似比=______,
(1)与(2)的面积比=______
(2)与(3)的相似比=______,
(2)与(3)的面积比=______1∶ 42∶ 34∶ 9猜想:相似三角形面积的比等于相似比的平方. 已知△ABC∽△ ,且相似比为k, AD、 分别是△ABC、△ 对应边BC、 上的高,求证:证明:∵△ABC∽△∴∴填一填探究3填一填探究3类似结论D'C'B'A'DCBA∽探究3结论:相似三角形对应中线的比等于相似比.A′C′B′CBAE′E类似结论探究3结论:相似三角形对应角的角平分线的比等于相似比. 1、相似三角形对应边成____,对应角______.
2、相似三角形对应边上的高、对应边上的中线、
对应角平分线的比都等于________.
3、相似三角形周长的比等于________,
相似三角形面积的比等于______________.
归纳相似比的平方相似三角形的性质比例相等相似比相似比展示测评1:1.相似三角形对应边的比为2∶3,那么相似比为_________,对应角的角平分线的比为______.2∶ 32 ∶ 32.两个相似三角形的相似比为1:4, 则对应高的比为_________,对应角的角平分线的比为_________. 1:41:4 例1:已知△ABC∽ △A′B ′C ′,BD和B ′D ′分别是△ABC和△A′B′C′中线,且AB=10,A′B′=2,BD=6。求B′D′的长。
解:∵ △ABC∽△A′B′C′∴ == B′D′=1.2答:B′D′的长为1.2。 (1)△ADE与△ABC相似吗?如果相似, 求它们的相似比. ABCDE1∶4 (2) △ADE的周长︰△ABC的周长=_______. 1∶4 例2 、如图,DE∥BC, DE = 1, BC = 4,(4)1.如果两个三角形相似,相似比为3∶5,则对应角的角平分线的比等于______.2.相似三角形对应边的比为2:5,
那么相似比为_______,
对应角的角平分线的比为______,
3∶5 2:5展示测评2:2:53、如果两个三角形相似,相似比为3∶5,那么对应角的角平分线的比等于多少?
4、相似三角形对应边的比为0.4,那么相似比为______,对应角的角平分线的比为______。3∶50.40.45、若两个三角形的对高之比为4:3,对应中线之比为_____4 : 35、把一个三角形变成和它相似的三角形,
(1)如果边长扩大为原来的5倍,那么面积扩大为原来的______倍。
(2)如果面积扩大为原来的100倍,那么边长扩大为原来的______倍。
(3)两个相似三角形的一对对应边分别是35厘米和14 厘米,①它们的周长差60厘米,这两个三角形的周长分别是______ ____。②它们的面积之和是58平方厘米,这两个三角形的面积分别是______________。2510100cm、40cm 50cm2、8cm26、已知△ABC∽△DEF,BG、EH分别是△ABC和 △DEF的角平分线,BC=6cm,EF=4cm,BG=4.8cm.求EH的长。解:∵ △ABC∽△DEF ∴ BC∶EF=BG∶EH6∶4=4.8∶EHEH=3.2(cm)答:EH的长为3.2cm。7、如图,在 ABCD中,若E是AB的中点,
则(1)?AEF与?CDF的相似比为______.
(2)若?AEF的面积为5cm2,
则?CDF的面积为______.BFEDCA1 : 220 cm2∵?AEF与?CDF 1、相似三角形对应边成____,对应角______.
2、相似三角形对应边上的高、对应边上的中线、
对应角平分线的比都等于________.
3、相似三角形周长的比等于________,
相似三角形面积的比等于______________.
课堂小结相似比的平方相似三角形的性质比例相等相似比相似比如图,一条河的两岸有一段是平行的,在河的两岸边每隔5米有一棵树,在北岸边每
隔60米有一根电线杆.小丽站在离南岸边15米的点P处看北岸,发现北岸相邻的两根
电线杆恰好被南岸的两棵树遮住,并且在这两棵树之间还有三棵树,则河宽为___米.课堂测试:30
隔60米有一根电线杆.小丽站在离南岸边15米的点P处看北岸,发现北岸相邻的两根
电线杆恰好被南岸的两棵树遮住,并且在这两棵树之间还有三棵树,则河宽为___米.引入:_相似三角形的性质学习目标1.掌握相似三角形的性质定理的内容及证明,进一步理解相似三角形的概念.
2.能运用相似三角形的性质定理来解决有关问题.
3.通过由特殊情况猜想到一般情况,渗透由特殊到一般的数学思想,感受数学的和谐美,并进一步养成严谨科学的学习品质.(1)什么叫相似三角形?
对应角相等、对应边成比例的三角形,叫做相似三角形.(2)如何判定两个三角形相似?①定义;
②预备定理(平行);
③两个角对应相等;两个三角形相似
④两边对应成比例,且夹角相等两个三角形相似
⑤三边对应成比例两个三角形相似;知识准备:ABCA/B/C/ ①相似三角形的对应角_____________
②相似三角形的对应边______________想一想: 它们还有哪些性质呢?温故知新(3)相似三角形有何性质?(1)一个三角形有三条重要线段:
________________(2)如果两个三角形全等,那么这些对应线段有什么关系?如果两个三角形相似,那么这些对应线段又有什么关系呢?提出问题:高、中线、角平分线(1)探究1∽可得: 观察这些数据,你会有怎样的猜想呢?合作探究:两角对应相等,两三角形相似∽已知所以∠B=∠B′( )相似三角形的对应角相等 ( )相似三角形的性质合作探究:∽所以(相似三角形的对应边成比例)∽相似三角形的性质结论:相似三角形对应高的比等于相似比.探究21231∶ 2当相似比=k时,面积比等于什么? (1)(2)(3)(1)与(2)的相似比=______,
(1)与(2)的面积比=______
(2)与(3)的相似比=______,
(2)与(3)的面积比=______1∶ 42∶ 34∶ 9猜想:相似三角形面积的比等于相似比的平方. 已知△ABC∽△ ,且相似比为k, AD、 分别是△ABC、△ 对应边BC、 上的高,求证:证明:∵△ABC∽△∴∴填一填探究3填一填探究3类似结论D'C'B'A'DCBA∽探究3结论:相似三角形对应中线的比等于相似比.A′C′B′CBAE′E类似结论探究3结论:相似三角形对应角的角平分线的比等于相似比. 1、相似三角形对应边成____,对应角______.
2、相似三角形对应边上的高、对应边上的中线、
对应角平分线的比都等于________.
3、相似三角形周长的比等于________,
相似三角形面积的比等于______________.
归纳相似比的平方相似三角形的性质比例相等相似比相似比展示测评1:1.相似三角形对应边的比为2∶3,那么相似比为_________,对应角的角平分线的比为______.2∶ 32 ∶ 32.两个相似三角形的相似比为1:4, 则对应高的比为_________,对应角的角平分线的比为_________. 1:41:4 例1:已知△ABC∽ △A′B ′C ′,BD和B ′D ′分别是△ABC和△A′B′C′中线,且AB=10,A′B′=2,BD=6。求B′D′的长。
解:∵ △ABC∽△A′B′C′∴ == B′D′=1.2答:B′D′的长为1.2。 (1)△ADE与△ABC相似吗?如果相似, 求它们的相似比. ABCDE1∶4 (2) △ADE的周长︰△ABC的周长=_______. 1∶4 例2 、如图,DE∥BC, DE = 1, BC = 4,(4)1.如果两个三角形相似,相似比为3∶5,则对应角的角平分线的比等于______.2.相似三角形对应边的比为2:5,
那么相似比为_______,
对应角的角平分线的比为______,
3∶5 2:5展示测评2:2:53、如果两个三角形相似,相似比为3∶5,那么对应角的角平分线的比等于多少?
4、相似三角形对应边的比为0.4,那么相似比为______,对应角的角平分线的比为______。3∶50.40.45、若两个三角形的对高之比为4:3,对应中线之比为_____4 : 35、把一个三角形变成和它相似的三角形,
(1)如果边长扩大为原来的5倍,那么面积扩大为原来的______倍。
(2)如果面积扩大为原来的100倍,那么边长扩大为原来的______倍。
(3)两个相似三角形的一对对应边分别是35厘米和14 厘米,①它们的周长差60厘米,这两个三角形的周长分别是______ ____。②它们的面积之和是58平方厘米,这两个三角形的面积分别是______________。2510100cm、40cm 50cm2、8cm26、已知△ABC∽△DEF,BG、EH分别是△ABC和 △DEF的角平分线,BC=6cm,EF=4cm,BG=4.8cm.求EH的长。解:∵ △ABC∽△DEF ∴ BC∶EF=BG∶EH6∶4=4.8∶EHEH=3.2(cm)答:EH的长为3.2cm。7、如图,在 ABCD中,若E是AB的中点,
则(1)?AEF与?CDF的相似比为______.
(2)若?AEF的面积为5cm2,
则?CDF的面积为______.BFEDCA1 : 220 cm2∵?AEF与?CDF 1、相似三角形对应边成____,对应角______.
2、相似三角形对应边上的高、对应边上的中线、
对应角平分线的比都等于________.
3、相似三角形周长的比等于________,
相似三角形面积的比等于______________.
课堂小结相似比的平方相似三角形的性质比例相等相似比相似比如图,一条河的两岸有一段是平行的,在河的两岸边每隔5米有一棵树,在北岸边每
隔60米有一根电线杆.小丽站在离南岸边15米的点P处看北岸,发现北岸相邻的两根
电线杆恰好被南岸的两棵树遮住,并且在这两棵树之间还有三棵树,则河宽为___米.课堂测试:30
