湖南省株洲市茶陵县云阳中学2015-2016学年八年级(下)第二次质检数学试卷(解析版)
文档属性
| 名称 | 湖南省株洲市茶陵县云阳中学2015-2016学年八年级(下)第二次质检数学试卷(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 187.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-11-02 16:35:31 | ||
图片预览


文档简介
2015-2016学年湖南省株洲市茶陵县云阳中学八年级(下)第二次质检数学试卷
一、选择题(每小题3分,共30分)
1.如图图形中,既是轴对称图形又是中心对称图形的是( )
A.
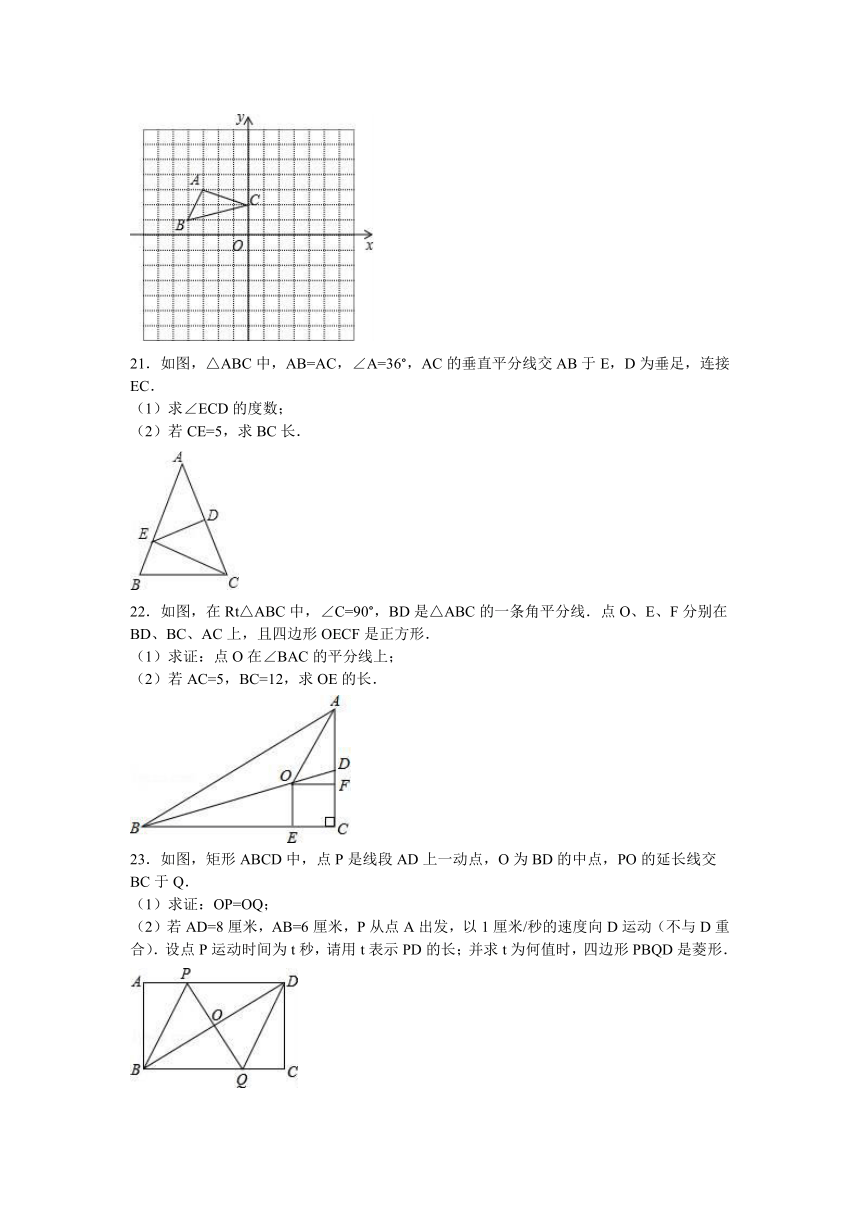
B.
C.
D.
2.一个多边形的内角和是外角和的2倍,则这个多边形的边数为( )
A.4
B.5
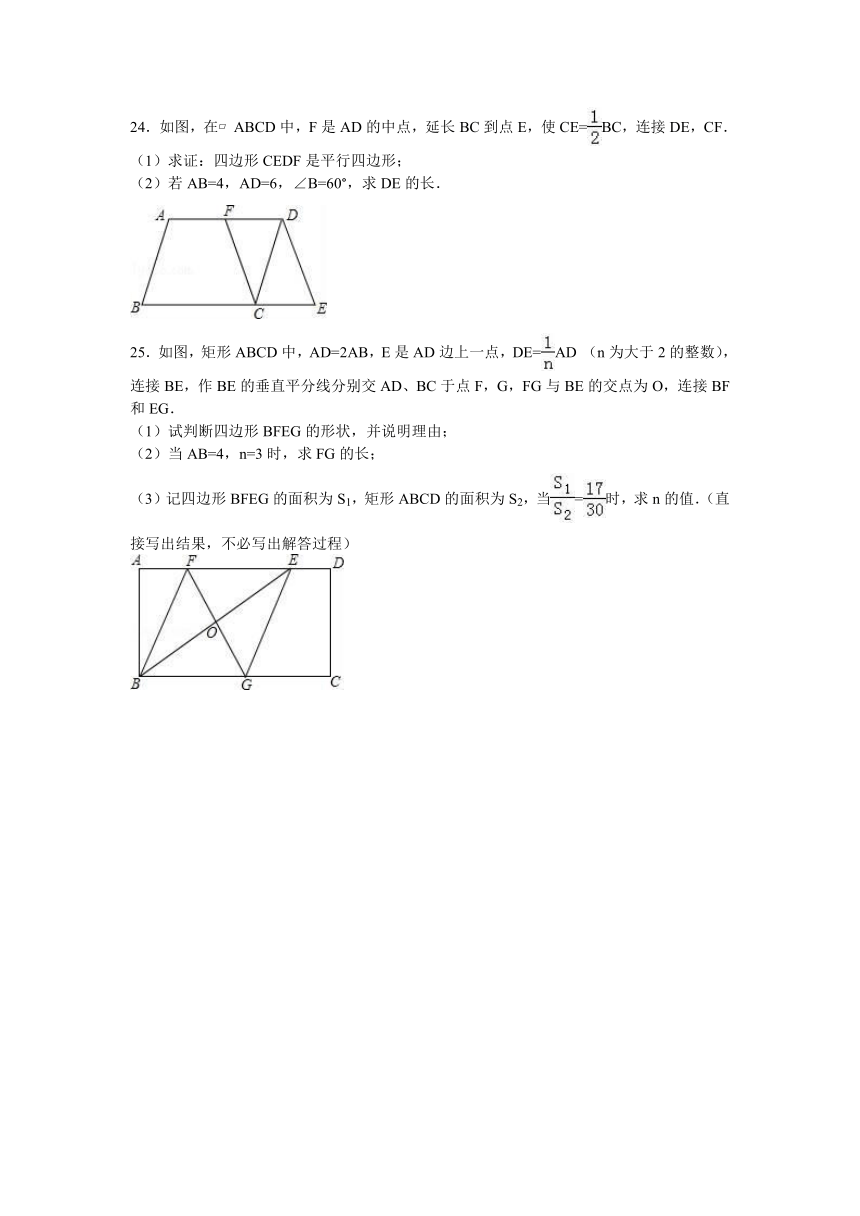
C.6
D.7
3.在平面直角坐标系中,点P(﹣20,a)与点Q(b,13)关于原点对称,则a+b的值为( )
A.33
B.﹣33
C.﹣7
D.7
4.下列各组数据中的三个数作为三角形的边长,其中能构成直角三角形的是( )
A.,,
B.1,,
C.6,7,8
D.2,3,4
5.如图,在Rt△ABC中,∠BAC=90°,AB=3,AC=4,D为BC的中点,则线段AD的长为( )
A.1.5
B.2
C.2.5
D.3
6.把一块直尺与一块三角板如图放置,若∠1=40°,则∠2的度数为( )
A.125°
B.120°
C.140°
D.130°
7.如图,正方形OABC的两边OA、OC分别在x轴、y轴上,点D(5,3)在边AB上,以C为中心,把△CDB旋转90°,则旋转后点D的对应点D′的坐标是( )
A.(2,10)
B.(﹣2,0)
C.(2,10)或(﹣2,0)
D.(10,2)或(﹣2,0)
8.如图,Rt△ABC中,AB=9,BC=6,∠B=90°,将△ABC折叠,使A点与BC的中点D重合,折痕为MN,则线段BN的长为( )
A.4
B.5
C.
D.
9.已知四边形ABCD是平行四边形,再从①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD四个条件中,选两个作为补充条件后,使得四边形ABCD是正方形,现有下列四种选法,其中错误的是( )
A.选①②
B.选②③
C.选①③
D.选②④
10.在平面直角坐标系中,孔明做走棋的游戏,其走法是:棋子从原点出发,第1步向右走1个单位,第2步向右走2个单位,第3步向上走1个单位,第4步向右走1个单位…依此类推,第n步的走法是:当n能被3整除时,则向上走1个单位;当n被3除,余数为1时,则向右走1个单位;当n被3除,余数为2时,则向右走2个单位,当走完第100步时,棋子所处位置的坐标是( )
A.(66,34)
B.(67,33)
C.
D.(99,34)
二、填空题(每小题3分,共24分)
11.在平面直角坐标中,点M(﹣2,3)在 象限.
12.如图,A,B,C三点在同一条直线上,∠A=∠C=90°,AB=CD,请添加一个适当的条件 ,使得△EAB≌△BCD.
13.如图,在矩形ABCD中,∠BOC=120°,AB=5,则BD的长为 .
14.如图,在菱形ABCD中,AB=10,AC=12,则它的面积是 .
15.已知a、b、c是△ABC的三边长,且满足关系式+|a﹣b|=0,则△ABC的形状为 .
16.如图,在 ABCD中,AB=3,BC=5,对角线AC、BD相交于点O,过点O作OE⊥AC,交AD于点E,连接CE,则△CDE的周长为 .
17.如图,D是△ABC内一点,BD⊥CD,AD=6,BD=4,CD=3,E、F、G、H分别是AB、AC、CD、BD的中点,则四边形EFGH的周长是 .
18.如图,在边长为8的正方形ABCD中,E是AB边上的一点,且AE=6,点Q为对角线AC上的动点,则△BEQ周长的最小值为 .
三、解答题(7个小题,共66分)
19.(1)计算:
+|﹣2|+(﹣1)0﹣()﹣1
(2)先化简,再求值:(3x+2)(3x﹣2)﹣5x(x﹣1)﹣(2x﹣1)2,其中x=﹣.
20.图中方格纸中每个小正方形的边长都是1个单位长度,△ABC的位置如图所示.请在图中
(1)作出△A1B1C1,使其与△ABC关于点O成中心对称.
(2)作出△A2B2C2,使其与△ABC关于直线y成轴对称.
21.如图,△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于E,D为垂足,连接EC.
(1)求∠ECD的度数;
(2)若CE=5,求BC长.
22.如图,在Rt△ABC中,∠C=90°,BD是△ABC的一条角平分线.点O、E、F分别在BD、BC、AC上,且四边形OECF是正方形.
(1)求证:点O在∠BAC的平分线上;
(2)若AC=5,BC=12,求OE的长.
23.如图,矩形ABCD中,点P是线段AD上一动点,O为BD的中点,PO的延长线交BC于Q.
(1)求证:OP=OQ;
(2)若AD=8厘米,AB=6厘米,P从点A出发,以1厘米/秒的速度向D运动(不与D重合).设点P运动时间为t秒,请用t表示PD的长;并求t为何值时,四边形PBQD是菱形.
24.如图,在 ABCD中,F是AD的中点,延长BC到点E,使CE=BC,连接DE,CF.
(1)求证:四边形CEDF是平行四边形;
(2)若AB=4,AD=6,∠B=60°,求DE的长.
25.如图,矩形ABCD中,AD=2AB,E是AD边上一点,DE=AD
(n为大于2的整数),连接BE,作BE的垂直平分线分别交AD、BC于点F,G,FG与BE的交点为O,连接BF和EG.
(1)试判断四边形BFEG的形状,并说明理由;
(2)当AB=4,n=3时,求FG的长;
(3)记四边形BFEG的面积为S1,矩形ABCD的面积为S2,当=时,求n的值.(直接写出结果,不必写出解答过程)
2015-2016学年湖南省株洲市茶陵县云阳中学八年级(下)第二次质检数学试卷
参考答案与试题解析
一、选择题(每小题3分,共30分)
1.如图图形中,既是轴对称图形又是中心对称图形的是( )
A.
B.
C.
D.
【考点】中心对称图形;轴对称图形.
【分析】根据轴对称图形与中心对称图形的概念求解.
【解答】解:A、不是轴对称图形,因为找不到任何这样的一条直线,沿这条直线对折后它的两部分能够重合;即不满足轴对称图形的定义.是中心对称图形.故错误;
B、不是轴对称图形,因为找不到任何这样的一条直线,沿这条直线对折后它的两部分能够重合;即不满足轴对称图形的定义.不是中心对称图形.故错误;
C、是轴对称图形,不是中心对称图形.故错误;
D、是轴对称图形.是中心对称图形,故正确.
故选D.
2.一个多边形的内角和是外角和的2倍,则这个多边形的边数为( )
A.4
B.5
C.6
D.7
【考点】多边形内角与外角.
【分析】多边形的外角和是360°,则内角和是2×360=720°.设这个多边形是n边形,内角和是(n﹣2) 180°,这样就得到一个关于n的方程组,从而求出边数n的值.
【解答】解:设这个多边形是n边形,根据题意,得
(n﹣2)×180°=2×360,
解得:n=6.
即这个多边形为六边形.
故选:C.
3.在平面直角坐标系中,点P(﹣20,a)与点Q(b,13)关于原点对称,则a+b的值为( )
A.33
B.﹣33
C.﹣7
D.7
【考点】关于原点对称的点的坐标.
【分析】先根据关于原点对称的点的坐标特点:横坐标与纵坐标都互为相反数,求出a与b的值,再代入计算即可.
【解答】解:∵点P(﹣20,a)与点Q(b,13)关于原点对称,
∴a=﹣13,b=20,
∴a+b=﹣13+20=7.
故选:D.
4.下列各组数据中的三个数作为三角形的边长,其中能构成直角三角形的是( )
A.,,
B.1,,
C.6,7,8
D.2,3,4
【考点】勾股定理的逆定理.
【分析】知道三条边的大小,用较小的两条边的平方和与最大的边的平方比较,如果相等,则三角形为直角三角形;否则不是.
【解答】解:A、()2+()2≠()2,不能构成直角三角形,故错误;
B、12+()2=()2,能构成直角三角形,故正确;
C、62+72≠82,不能构成直角三角形,故错误;
D、22+32≠42,不能构成直角三角形,故错误.
故选:B.
5.如图,在Rt△ABC中,∠BAC=90°,AB=3,AC=4,D为BC的中点,则线段AD的长为( )
A.1.5
B.2
C.2.5
D.3
【考点】直角三角形斜边上的中线.
【分析】先利用勾股定理求出斜边BC的长,再根据直角三角形斜边上的中线等于斜边的一半即可求解.
【解答】解:∵在Rt△ABC中,∠BAC=90°,AB=3,AC=4,
∴BC==5,
∵D为BC的中点,
∴AD=BC=2.5.
故选C.
6.把一块直尺与一块三角板如图放置,若∠1=40°,则∠2的度数为( )
A.125°
B.120°
C.140°
D.130°
【考点】平行线的性质;直角三角形的性质.
【分析】根据矩形性质得出EF∥GH,推出∠FCD=∠2,代入∠FCD=∠1+∠A求出即可.
【解答】解:
∵EF∥GH,
∴∠FCD=∠2,
∵∠FCD=∠1+∠A,∠1=40°,∠A=90°,
∴∠2=∠FCD=130°,
故选D.
7.如图,正方形OABC的两边OA、OC分别在x轴、y轴上,点D(5,3)在边AB上,以C为中心,把△CDB旋转90°,则旋转后点D的对应点D′的坐标是( )
A.(2,10)
B.(﹣2,0)
C.(2,10)或(﹣2,0)
D.(10,2)或(﹣2,0)
【考点】坐标与图形变化-旋转.
【分析】分顺时针旋转和逆时针旋转两种情况讨论解答即可.
【解答】解:∵点D(5,3)在边AB上,
∴BC=5,BD=5﹣3=2,
①若顺时针旋转,则点D′在x轴上,OD′=2,
所以,D′(﹣2,0),
②若逆时针旋转,则点D′到x轴的距离为10,到y轴的距离为2,
所以,D′(2,10),
综上所述,点D′的坐标为(2,10)或(﹣2,0).
故选:C.
8.如图,Rt△ABC中,AB=9,BC=6,∠B=90°,将△ABC折叠,使A点与BC的中点D重合,折痕为MN,则线段BN的长为( )
A.4
B.5
C.
D.
【考点】翻折变换(折叠问题).
【分析】设BN=x,则由折叠的性质可得DN=AN=9﹣x,根据中点的定义可得BD=3,在Rt△BND中,根据勾股定理可得关于x的方程,解方程即可求解.
【解答】解:设BN=x,由折叠的性质可得DN=AN=9﹣x,
∵D是BC的中点,
∴BD=3,
在Rt△NBD中,x2+32=(9﹣x)2,
解得x=4.
即BN=4.
故选A.
9.已知四边形ABCD是平行四边形,再从①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD四个条件中,选两个作为补充条件后,使得四边形ABCD是正方形,现有下列四种选法,其中错误的是( )
A.选①②
B.选②③
C.选①③
D.选②④
【考点】正方形的判定;平行四边形的性质.
【分析】要判定是正方形,则需能判定它既是菱形又是矩形.
【解答】解:A、由①得有一组邻边相等的平行四边形是菱形,由②得有一个角是直角的平行四边形是矩形,所以平行四边形ABCD是正方形,正确,故本选项不符合题意;
B、由②得有一个角是直角的平行四边形是矩形,由③得对角线相等的平行四边形是矩形,所以不能得出平行四边形ABCD是正方形,错误,故本选项符合题意;
C、由①得有一组邻边相等的平行四边形是菱形,由③得对角线相等的平行四边形是矩形,所以平行四边形ABCD是正方形,正确,故本选项不符合题意;
D、由②得有一个角是直角的平行四边形是矩形,由④得对角线互相垂直的平行四边形是菱形,所以平行四边形ABCD是正方形,正确,故本选项不符合题意.
故选:B.
10.在平面直角坐标系中,孔明做走棋的游戏,其走法是:棋子从原点出发,第1步向右走1个单位,第2步向右走2个单位,第3步向上走1个单位,第4步向右走1个单位…依此类推,第n步的走法是:当n能被3整除时,则向上走1个单位;当n被3除,余数为1时,则向右走1个单位;当n被3除,余数为2时,则向右走2个单位,当走完第100步时,棋子所处位置的坐标是( )
A.(66,34)
B.(67,33)
C.
D.(99,34)
【考点】坐标确定位置;规律型:点的坐标.
【分析】根据走法,每3步为一个循环组依次循环,且一个循环组内向右3个单位,向上1个单位,用100除以3,然后根据商和余数的情况确定出所处位置的横坐标与纵坐标即可.
【解答】解:由题意得,每3步为一个循环组依次循环,且一个循环组内向右3个单位,向上1个单位,
∵100÷3=33余1,
∴走完第100步,为第34个循环组的第1步,
所处位置的横坐标为33×3+1=100,
纵坐标为33×1=33,
∴棋子所处位置的坐标是.
故选:C.
二、填空题(每小题3分,共24分)
11.在平面直角坐标中,点M(﹣2,3)在 二 象限.
【考点】点的坐标.
【分析】由于点M的横坐标为负数,纵坐标为正数,根据各象限内点的坐标的符号特征即可求解.
【解答】解:点M(﹣2,3)在二象限.
故答案为二.
12.如图,A,B,C三点在同一条直线上,∠A=∠C=90°,AB=CD,请添加一个适当的条件 AE=CB ,使得△EAB≌△BCD.
【考点】全等三角形的判定.
【分析】可以根据全等三角形的不同的判定方法添加不同的条件.
【解答】解:∵∠A=∠C=90°,AB=CD,
∴若利用“SAS”,可添加AE=CB,
若利用“HL”,可添加EB=BD,
若利用“ASA”或“AAS”,可添加∠EBD=90°,
若添加∠E=∠DBC,可利用“AAS”证明.
综上所述,可添加的条件为AE=CB(或EB=BD或∠EBD=90°或∠E=∠DBC等).
故答案为:AE=CB.
13.如图,在矩形ABCD中,∠BOC=120°,AB=5,则BD的长为 10 .
【考点】矩形的性质.
【分析】根据矩形性质求出BD=2BO,OA=OB,求出∠AOB=60°,得出等边三角形AOB,求出BO=AB,即可求出答案.
【解答】解:∵四边形ABCD是矩形,
∴AC=2AO,BD=2BO,AC=BD,
∴OA=OB,
∵∠BOC=120°,
∴∠AOB=60°,
∴△AOB是等边三角形,
∴OB=AB=5,
∴BD=2BO=10,
故答案为:10.
14.如图,在菱形ABCD中,AB=10,AC=12,则它的面积是 96 .
【考点】菱形的性质.
【分析】首先根据勾股定理可求出BO的长,进而求出BD的长,再根据菱形的面积等于对角线乘积的一半列式计算即可得解.
【解答】解:∵四边形ABCD是菱形,
∴AC⊥BD,
∵AC=12,
∴AO=6,
∵AB=10,
∴BO==8,
∴BD=16,
∴菱形的面积S=AC BD=×16×12=96.
故答案为:96.
15.已知a、b、c是△ABC的三边长,且满足关系式+|a﹣b|=0,则△ABC的形状为 等腰直角三角形 .
【考点】勾股定理的逆定理;非负数的性质:绝对值;非负数的性质:算术平方根;等腰直角三角形.
【分析】已知等式左边为两个非负数之和,根据两非负数之和为0,两非负数同时为0,可得出c2=a2+b2,且a=b,利用勾股定理的逆定理可得出∠C为直角,进而确定出三角形ABC为等腰直角三角形.
【解答】解:∵+|a﹣b|=0,
∴c2﹣a2﹣b2=0,且a﹣b=0,
∴c2=a2+b2,且a=b,
则△ABC为等腰直角三角形.
故答案为:等腰直角三角形
16.如图,在 ABCD中,AB=3,BC=5,对角线AC、BD相交于点O,过点O作OE⊥AC,交AD于点E,连接CE,则△CDE的周长为 8 .
【考点】线段垂直平分线的性质;平行四边形的性质.
【分析】根据平行四边形的性质,得知AO=OC,由于OE⊥AC,根据线段垂直平分线的性质,可知AE=EC,则△CDE的周长为CD与AD之和,即可得解.
【解答】解:根据平行四边形的性质,
∴AO=OC,
∵OE⊥AC,
∴OE为AC的垂直平分线,
∴AE=EC,
∴△CDE的周长为:CD+AD=5+3=8,
故答案为:8.
17.如图,D是△ABC内一点,BD⊥CD,AD=6,BD=4,CD=3,E、F、G、H分别是AB、AC、CD、BD的中点,则四边形EFGH的周长是 11 .
【考点】三角形中位线定理;勾股定理.
【分析】利用勾股定理列式求出BC的长,再根据三角形的中位线平行于第三边并且等于第三边的一半求出EH=FG=AD,EF=GH=BC,然后代入数据进行计算即可得解.
【解答】解:∵BD⊥CD,BD=4,CD=3,
∴BC===5,
∵E、F、G、H分别是AB、AC、CD、BD的中点,
∴EH=FG=AD,EF=GH=BC,
∴四边形EFGH的周长=EH+GH+FG+EF=AD+BC,
又∵AD=6,
∴四边形EFGH的周长=6+5=11.
故答案为:11.
18.如图,在边长为8的正方形ABCD中,E是AB边上的一点,且AE=6,点Q为对角线AC上的动点,则△BEQ周长的最小值为 12 .
【考点】正方形的性质;轴对称-最短路线问题.
【分析】连接BD,DE,根据正方形的性质可知点B与点D关于直线AC对称,故DE的长即为BQ+QE的最小值,进而可得出结论.
【解答】解:连接BD,DE,
∵四边形ABCD是正方形,
∴点B与点D关于直线AC对称,
∴DE的长即为BQ+QE的最小值,
∵AB=8,AE=6,
∴DE=BQ+QE==10,
∵AB=8,AE=6,
∴BE=2,
∴△BEQ周长的最小值=DE+BE=10+2=12.
故答案为:12.
三、解答题(7个小题,共66分)
19.(1)计算:
+|﹣2|+(﹣1)0﹣()﹣1
(2)先化简,再求值:(3x+2)(3x﹣2)﹣5x(x﹣1)﹣(2x﹣1)2,其中x=﹣.
【考点】整式的混合运算—化简求值;实数的运算;零指数幂;负整数指数幂.
【分析】(1)先根据二次根式的性质,绝对值,零指数幂,负整数指数幂分别求出每一部分的值,再代入求出即可;
(2)先算乘法,再合并同类项,最后代入求出即可.
【解答】解:(1)原式=2+2﹣﹣1﹣2
=﹣1;
(2)(3x+2)(3x﹣2)﹣5x(x﹣1)﹣(2x﹣1)2
=9x2﹣4﹣5x2+5x﹣4x2+4x﹣1
=9x﹣5,
当x=﹣,时,原式=9×(﹣)﹣5=﹣8.
20.图中方格纸中每个小正方形的边长都是1个单位长度,△ABC的位置如图所示.请在图中
(1)作出△A1B1C1,使其与△ABC关于点O成中心对称.
(2)作出△A2B2C2,使其与△ABC关于直线y成轴对称.
【考点】作图-旋转变换;作图-轴对称变换.
【分析】(1)作出各点关于原点的对称点,再顺次连接即可;
(2)作出各点关于y轴的对称点,再顺次连接即可.
【解答】解:(1)如图,△A1B1C1即为所求;
(2)如图,△A2B2C2即为所求.
21.如图,△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于E,D为垂足,连接EC.
(1)求∠ECD的度数;
(2)若CE=5,求BC长.
【考点】线段垂直平分线的性质;等腰三角形的性质.
【分析】(1)ED是AC的垂直平分线,可得AE=EC;∠A=∠C;已知∠A=36,即可求得;
(2)△ABC中,AB=AC,∠A=36°,可得∠B=72°又∠BEC=∠A+∠ECA=72°,所以,得BC=EC=5;
【解答】解:(1)∵DE垂直平分AC,
∴CE=AE,∴∠ECD=∠A=36°;
(2)∵AB=AC,∠A=36°,
∴∠B=∠ACB=72°,
∴∠BEC=∠A+∠ECD=72°,
∴∠BEC=∠B,
∴BC=EC=5.
答:(1)∠ECD的度数是36°;
(2)BC长是5.
22.如图,在Rt△ABC中,∠C=90°,BD是△ABC的一条角平分线.点O、E、F分别在BD、BC、AC上,且四边形OECF是正方形.
(1)求证:点O在∠BAC的平分线上;
(2)若AC=5,BC=12,求OE的长.
【考点】角平分线的性质;全等三角形的判定与性质;正方形的性质.
【分析】(1)过点O作OM⊥AB,由角平分线的性质得OE=OM,由正方形的性质得OE=OF,易得OM=OF,由角平分线的判定定理得点O在∠BAC的平分线上;
(2)由勾股定理得AB的长,利用方程思想解得结果.
【解答】(1)证明:过点O作OM⊥AB,
∵BD是∠ABC的一条角平分线,
∴OE=OM,
∵四边形OECF是正方形,
∴OE=OF,
∴OF=OM,
∴AO是∠BAC的角平分线,即点O在∠BAC的平分线上;
(2)解:∵在Rt△ABC中,AC=5,BC=12,
∴AB===13,
设CE=CF=x,BE=BM=y,AM=AF=z,
∴,
解得:,
∴CE=2,
∴OE=2.
23.如图,矩形ABCD中,点P是线段AD上一动点,O为BD的中点,PO的延长线交BC于Q.
(1)求证:OP=OQ;
(2)若AD=8厘米,AB=6厘米,P从点A出发,以1厘米/秒的速度向D运动(不与D重合).设点P运动时间为t秒,请用t表示PD的长;并求t为何值时,四边形PBQD是菱形.
【考点】相似三角形的判定与性质;全等三角形的判定与性质;勾股定理;菱形的性质;矩形的性质.
【分析】(1)本题需先根据四边形ABCD是矩形,得出AD∥BC,∠PDO=∠QBO,再根据O为BD的中点得出△POD≌△QOB,即可证出OP=OQ.
(2)本题需先根据已知条件得出∠A的度数,再根据AD=8厘米,AB=6厘米,得出BD和OD的长,再根据四边形PBQD是菱形时,即可求出t的值,判断出四边形PBQD是菱形.
【解答】(1)证明:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠PDO=∠QBO,
又∵O为BD的中点,
∴OB=OD,
在△POD与△QOB中,
∵
∴△POD≌△QOB(ASA),
∴OP=OQ;
(2)解:PD=8﹣t,
∵四边形PBQD是菱形,
∴PD=BP=8﹣t,
∵四边形ABCD是矩形,
∴∠A=90°,
在Rt△ABP中,由勾股定理得:AB2+AP2=BP2,
即62+t2=(8﹣t)2,
解得:t=,
即运动时间为秒时,四边形PBQD是菱形.
24.如图,在 ABCD中,F是AD的中点,延长BC到点E,使CE=BC,连接DE,CF.
(1)求证:四边形CEDF是平行四边形;
(2)若AB=4,AD=6,∠B=60°,求DE的长.
【考点】平行四边形的判定与性质;含30度角的直角三角形;勾股定理.
【分析】(1)由“平行四边形的对边平行且相等”的性质推知AD∥BC,且AD=BC;然后根据中点的定义、结合已知条件推知四边形CEDF的对边平行且相等(DF=CE,且DF∥CE),即四边形CEDF是平行四边形;
(2)如图,过点D作DH⊥BE于点H,构造含30度角的直角△DCH和直角△DHE.通过解直角△DCH和在直角△DHE中运用勾股定理来求线段ED的长度.
【解答】证明:(1)在 ABCD中,AD∥BC,且AD=BC.
∵F是AD的中点,
∴DF=.
又∵CE=BC,
∴DF=CE,且DF∥CE,
∴四边形CEDF是平行四边形;
(2)解:如图,过点D作DH⊥BE于点H.
在 ABCD中,∵∠B=60°,
∴∠DCE=60°.
∵AB=4,
∴CD=AB=4,
∴CH=CD=2,DH=2.
在 CEDF中,CE=DF=AD=3,则EH=1.
∴在Rt△DHE中,根据勾股定理知DE==.
25.如图,矩形ABCD中,AD=2AB,E是AD边上一点,DE=AD
(n为大于2的整数),连接BE,作BE的垂直平分线分别交AD、BC于点F,G,FG与BE的交点为O,连接BF和EG.
(1)试判断四边形BFEG的形状,并说明理由;
(2)当AB=4,n=3时,求FG的长;
(3)记四边形BFEG的面积为S1,矩形ABCD的面积为S2,当=时,求n的值.(直接写出结果,不必写出解答过程)
【考点】四边形综合题.
【分析】(1)先求证△EFO≌△BGO,可得EF=BG,再根据△BOF≌△EOF,可得EF=BF;即可证明四边形BFEG为菱形;
(2)根据菱形面积不同的计算公式(底乘高和对角线乘积的一半两种计算方式)可计算FG的长度;
(3)根据菱形面积底乘高的计算方式可以求出BG长度,根据勾股定理可求出AF的长度,即可求出ED的长度,即可计算n的值
【解答】解:(1)∵AD∥BC,
∴∠EFO=∠BGO,
∵FG为BE的垂直平分线,
∴BO=OE;
∵在△EFO和△BGO中,
,
∴△EFO≌△BGO,
∴EF=BG,
∵AD∥BC,
∴四边形BGEF为平行四边形,
∵FG是BE的垂直平分线,
∴FB=FE,
∴平行四边形BGEF为菱形;
(2)当AB=4,n=3时,
∴AD=8,AE=,
由勾股定理得,BE=,
AF=AE﹣EF=AE﹣BF,
在Rt△ABF中AB2+AF2=BF2,即(﹣BF)2+42=BF2,
解得,BF=,
则AF=,
菱形BGEF面积=BE FG=EF AB,即××FG=×4,
解得,FG=5;
(3)设AB=x,则DE=,
S1=BG AB,S2=BC AB
当=时,
=,
则BG=x,
在Rt△ABF中AB2+AF2=BF2,计算可得AF=x,
∴AE=AF+FE=AF+BG=x,DE=AD﹣AE=x,
∴x=,
∴n=6.
2016年11月2日
一、选择题(每小题3分,共30分)
1.如图图形中,既是轴对称图形又是中心对称图形的是( )
A.
B.
C.
D.
2.一个多边形的内角和是外角和的2倍,则这个多边形的边数为( )
A.4
B.5
C.6
D.7
3.在平面直角坐标系中,点P(﹣20,a)与点Q(b,13)关于原点对称,则a+b的值为( )
A.33
B.﹣33
C.﹣7
D.7
4.下列各组数据中的三个数作为三角形的边长,其中能构成直角三角形的是( )
A.,,
B.1,,
C.6,7,8
D.2,3,4
5.如图,在Rt△ABC中,∠BAC=90°,AB=3,AC=4,D为BC的中点,则线段AD的长为( )
A.1.5
B.2
C.2.5
D.3
6.把一块直尺与一块三角板如图放置,若∠1=40°,则∠2的度数为( )
A.125°
B.120°
C.140°
D.130°
7.如图,正方形OABC的两边OA、OC分别在x轴、y轴上,点D(5,3)在边AB上,以C为中心,把△CDB旋转90°,则旋转后点D的对应点D′的坐标是( )
A.(2,10)
B.(﹣2,0)
C.(2,10)或(﹣2,0)
D.(10,2)或(﹣2,0)
8.如图,Rt△ABC中,AB=9,BC=6,∠B=90°,将△ABC折叠,使A点与BC的中点D重合,折痕为MN,则线段BN的长为( )
A.4
B.5
C.
D.
9.已知四边形ABCD是平行四边形,再从①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD四个条件中,选两个作为补充条件后,使得四边形ABCD是正方形,现有下列四种选法,其中错误的是( )
A.选①②
B.选②③
C.选①③
D.选②④
10.在平面直角坐标系中,孔明做走棋的游戏,其走法是:棋子从原点出发,第1步向右走1个单位,第2步向右走2个单位,第3步向上走1个单位,第4步向右走1个单位…依此类推,第n步的走法是:当n能被3整除时,则向上走1个单位;当n被3除,余数为1时,则向右走1个单位;当n被3除,余数为2时,则向右走2个单位,当走完第100步时,棋子所处位置的坐标是( )
A.(66,34)
B.(67,33)
C.
D.(99,34)
二、填空题(每小题3分,共24分)
11.在平面直角坐标中,点M(﹣2,3)在 象限.
12.如图,A,B,C三点在同一条直线上,∠A=∠C=90°,AB=CD,请添加一个适当的条件 ,使得△EAB≌△BCD.
13.如图,在矩形ABCD中,∠BOC=120°,AB=5,则BD的长为 .
14.如图,在菱形ABCD中,AB=10,AC=12,则它的面积是 .
15.已知a、b、c是△ABC的三边长,且满足关系式+|a﹣b|=0,则△ABC的形状为 .
16.如图,在 ABCD中,AB=3,BC=5,对角线AC、BD相交于点O,过点O作OE⊥AC,交AD于点E,连接CE,则△CDE的周长为 .
17.如图,D是△ABC内一点,BD⊥CD,AD=6,BD=4,CD=3,E、F、G、H分别是AB、AC、CD、BD的中点,则四边形EFGH的周长是 .
18.如图,在边长为8的正方形ABCD中,E是AB边上的一点,且AE=6,点Q为对角线AC上的动点,则△BEQ周长的最小值为 .
三、解答题(7个小题,共66分)
19.(1)计算:
+|﹣2|+(﹣1)0﹣()﹣1
(2)先化简,再求值:(3x+2)(3x﹣2)﹣5x(x﹣1)﹣(2x﹣1)2,其中x=﹣.
20.图中方格纸中每个小正方形的边长都是1个单位长度,△ABC的位置如图所示.请在图中
(1)作出△A1B1C1,使其与△ABC关于点O成中心对称.
(2)作出△A2B2C2,使其与△ABC关于直线y成轴对称.
21.如图,△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于E,D为垂足,连接EC.
(1)求∠ECD的度数;
(2)若CE=5,求BC长.
22.如图,在Rt△ABC中,∠C=90°,BD是△ABC的一条角平分线.点O、E、F分别在BD、BC、AC上,且四边形OECF是正方形.
(1)求证:点O在∠BAC的平分线上;
(2)若AC=5,BC=12,求OE的长.
23.如图,矩形ABCD中,点P是线段AD上一动点,O为BD的中点,PO的延长线交BC于Q.
(1)求证:OP=OQ;
(2)若AD=8厘米,AB=6厘米,P从点A出发,以1厘米/秒的速度向D运动(不与D重合).设点P运动时间为t秒,请用t表示PD的长;并求t为何值时,四边形PBQD是菱形.
24.如图,在 ABCD中,F是AD的中点,延长BC到点E,使CE=BC,连接DE,CF.
(1)求证:四边形CEDF是平行四边形;
(2)若AB=4,AD=6,∠B=60°,求DE的长.
25.如图,矩形ABCD中,AD=2AB,E是AD边上一点,DE=AD
(n为大于2的整数),连接BE,作BE的垂直平分线分别交AD、BC于点F,G,FG与BE的交点为O,连接BF和EG.
(1)试判断四边形BFEG的形状,并说明理由;
(2)当AB=4,n=3时,求FG的长;
(3)记四边形BFEG的面积为S1,矩形ABCD的面积为S2,当=时,求n的值.(直接写出结果,不必写出解答过程)
2015-2016学年湖南省株洲市茶陵县云阳中学八年级(下)第二次质检数学试卷
参考答案与试题解析
一、选择题(每小题3分,共30分)
1.如图图形中,既是轴对称图形又是中心对称图形的是( )
A.
B.
C.
D.
【考点】中心对称图形;轴对称图形.
【分析】根据轴对称图形与中心对称图形的概念求解.
【解答】解:A、不是轴对称图形,因为找不到任何这样的一条直线,沿这条直线对折后它的两部分能够重合;即不满足轴对称图形的定义.是中心对称图形.故错误;
B、不是轴对称图形,因为找不到任何这样的一条直线,沿这条直线对折后它的两部分能够重合;即不满足轴对称图形的定义.不是中心对称图形.故错误;
C、是轴对称图形,不是中心对称图形.故错误;
D、是轴对称图形.是中心对称图形,故正确.
故选D.
2.一个多边形的内角和是外角和的2倍,则这个多边形的边数为( )
A.4
B.5
C.6
D.7
【考点】多边形内角与外角.
【分析】多边形的外角和是360°,则内角和是2×360=720°.设这个多边形是n边形,内角和是(n﹣2) 180°,这样就得到一个关于n的方程组,从而求出边数n的值.
【解答】解:设这个多边形是n边形,根据题意,得
(n﹣2)×180°=2×360,
解得:n=6.
即这个多边形为六边形.
故选:C.
3.在平面直角坐标系中,点P(﹣20,a)与点Q(b,13)关于原点对称,则a+b的值为( )
A.33
B.﹣33
C.﹣7
D.7
【考点】关于原点对称的点的坐标.
【分析】先根据关于原点对称的点的坐标特点:横坐标与纵坐标都互为相反数,求出a与b的值,再代入计算即可.
【解答】解:∵点P(﹣20,a)与点Q(b,13)关于原点对称,
∴a=﹣13,b=20,
∴a+b=﹣13+20=7.
故选:D.
4.下列各组数据中的三个数作为三角形的边长,其中能构成直角三角形的是( )
A.,,
B.1,,
C.6,7,8
D.2,3,4
【考点】勾股定理的逆定理.
【分析】知道三条边的大小,用较小的两条边的平方和与最大的边的平方比较,如果相等,则三角形为直角三角形;否则不是.
【解答】解:A、()2+()2≠()2,不能构成直角三角形,故错误;
B、12+()2=()2,能构成直角三角形,故正确;
C、62+72≠82,不能构成直角三角形,故错误;
D、22+32≠42,不能构成直角三角形,故错误.
故选:B.
5.如图,在Rt△ABC中,∠BAC=90°,AB=3,AC=4,D为BC的中点,则线段AD的长为( )
A.1.5
B.2
C.2.5
D.3
【考点】直角三角形斜边上的中线.
【分析】先利用勾股定理求出斜边BC的长,再根据直角三角形斜边上的中线等于斜边的一半即可求解.
【解答】解:∵在Rt△ABC中,∠BAC=90°,AB=3,AC=4,
∴BC==5,
∵D为BC的中点,
∴AD=BC=2.5.
故选C.
6.把一块直尺与一块三角板如图放置,若∠1=40°,则∠2的度数为( )
A.125°
B.120°
C.140°
D.130°
【考点】平行线的性质;直角三角形的性质.
【分析】根据矩形性质得出EF∥GH,推出∠FCD=∠2,代入∠FCD=∠1+∠A求出即可.
【解答】解:
∵EF∥GH,
∴∠FCD=∠2,
∵∠FCD=∠1+∠A,∠1=40°,∠A=90°,
∴∠2=∠FCD=130°,
故选D.
7.如图,正方形OABC的两边OA、OC分别在x轴、y轴上,点D(5,3)在边AB上,以C为中心,把△CDB旋转90°,则旋转后点D的对应点D′的坐标是( )
A.(2,10)
B.(﹣2,0)
C.(2,10)或(﹣2,0)
D.(10,2)或(﹣2,0)
【考点】坐标与图形变化-旋转.
【分析】分顺时针旋转和逆时针旋转两种情况讨论解答即可.
【解答】解:∵点D(5,3)在边AB上,
∴BC=5,BD=5﹣3=2,
①若顺时针旋转,则点D′在x轴上,OD′=2,
所以,D′(﹣2,0),
②若逆时针旋转,则点D′到x轴的距离为10,到y轴的距离为2,
所以,D′(2,10),
综上所述,点D′的坐标为(2,10)或(﹣2,0).
故选:C.
8.如图,Rt△ABC中,AB=9,BC=6,∠B=90°,将△ABC折叠,使A点与BC的中点D重合,折痕为MN,则线段BN的长为( )
A.4
B.5
C.
D.
【考点】翻折变换(折叠问题).
【分析】设BN=x,则由折叠的性质可得DN=AN=9﹣x,根据中点的定义可得BD=3,在Rt△BND中,根据勾股定理可得关于x的方程,解方程即可求解.
【解答】解:设BN=x,由折叠的性质可得DN=AN=9﹣x,
∵D是BC的中点,
∴BD=3,
在Rt△NBD中,x2+32=(9﹣x)2,
解得x=4.
即BN=4.
故选A.
9.已知四边形ABCD是平行四边形,再从①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD四个条件中,选两个作为补充条件后,使得四边形ABCD是正方形,现有下列四种选法,其中错误的是( )
A.选①②
B.选②③
C.选①③
D.选②④
【考点】正方形的判定;平行四边形的性质.
【分析】要判定是正方形,则需能判定它既是菱形又是矩形.
【解答】解:A、由①得有一组邻边相等的平行四边形是菱形,由②得有一个角是直角的平行四边形是矩形,所以平行四边形ABCD是正方形,正确,故本选项不符合题意;
B、由②得有一个角是直角的平行四边形是矩形,由③得对角线相等的平行四边形是矩形,所以不能得出平行四边形ABCD是正方形,错误,故本选项符合题意;
C、由①得有一组邻边相等的平行四边形是菱形,由③得对角线相等的平行四边形是矩形,所以平行四边形ABCD是正方形,正确,故本选项不符合题意;
D、由②得有一个角是直角的平行四边形是矩形,由④得对角线互相垂直的平行四边形是菱形,所以平行四边形ABCD是正方形,正确,故本选项不符合题意.
故选:B.
10.在平面直角坐标系中,孔明做走棋的游戏,其走法是:棋子从原点出发,第1步向右走1个单位,第2步向右走2个单位,第3步向上走1个单位,第4步向右走1个单位…依此类推,第n步的走法是:当n能被3整除时,则向上走1个单位;当n被3除,余数为1时,则向右走1个单位;当n被3除,余数为2时,则向右走2个单位,当走完第100步时,棋子所处位置的坐标是( )
A.(66,34)
B.(67,33)
C.
D.(99,34)
【考点】坐标确定位置;规律型:点的坐标.
【分析】根据走法,每3步为一个循环组依次循环,且一个循环组内向右3个单位,向上1个单位,用100除以3,然后根据商和余数的情况确定出所处位置的横坐标与纵坐标即可.
【解答】解:由题意得,每3步为一个循环组依次循环,且一个循环组内向右3个单位,向上1个单位,
∵100÷3=33余1,
∴走完第100步,为第34个循环组的第1步,
所处位置的横坐标为33×3+1=100,
纵坐标为33×1=33,
∴棋子所处位置的坐标是.
故选:C.
二、填空题(每小题3分,共24分)
11.在平面直角坐标中,点M(﹣2,3)在 二 象限.
【考点】点的坐标.
【分析】由于点M的横坐标为负数,纵坐标为正数,根据各象限内点的坐标的符号特征即可求解.
【解答】解:点M(﹣2,3)在二象限.
故答案为二.
12.如图,A,B,C三点在同一条直线上,∠A=∠C=90°,AB=CD,请添加一个适当的条件 AE=CB ,使得△EAB≌△BCD.
【考点】全等三角形的判定.
【分析】可以根据全等三角形的不同的判定方法添加不同的条件.
【解答】解:∵∠A=∠C=90°,AB=CD,
∴若利用“SAS”,可添加AE=CB,
若利用“HL”,可添加EB=BD,
若利用“ASA”或“AAS”,可添加∠EBD=90°,
若添加∠E=∠DBC,可利用“AAS”证明.
综上所述,可添加的条件为AE=CB(或EB=BD或∠EBD=90°或∠E=∠DBC等).
故答案为:AE=CB.
13.如图,在矩形ABCD中,∠BOC=120°,AB=5,则BD的长为 10 .
【考点】矩形的性质.
【分析】根据矩形性质求出BD=2BO,OA=OB,求出∠AOB=60°,得出等边三角形AOB,求出BO=AB,即可求出答案.
【解答】解:∵四边形ABCD是矩形,
∴AC=2AO,BD=2BO,AC=BD,
∴OA=OB,
∵∠BOC=120°,
∴∠AOB=60°,
∴△AOB是等边三角形,
∴OB=AB=5,
∴BD=2BO=10,
故答案为:10.
14.如图,在菱形ABCD中,AB=10,AC=12,则它的面积是 96 .
【考点】菱形的性质.
【分析】首先根据勾股定理可求出BO的长,进而求出BD的长,再根据菱形的面积等于对角线乘积的一半列式计算即可得解.
【解答】解:∵四边形ABCD是菱形,
∴AC⊥BD,
∵AC=12,
∴AO=6,
∵AB=10,
∴BO==8,
∴BD=16,
∴菱形的面积S=AC BD=×16×12=96.
故答案为:96.
15.已知a、b、c是△ABC的三边长,且满足关系式+|a﹣b|=0,则△ABC的形状为 等腰直角三角形 .
【考点】勾股定理的逆定理;非负数的性质:绝对值;非负数的性质:算术平方根;等腰直角三角形.
【分析】已知等式左边为两个非负数之和,根据两非负数之和为0,两非负数同时为0,可得出c2=a2+b2,且a=b,利用勾股定理的逆定理可得出∠C为直角,进而确定出三角形ABC为等腰直角三角形.
【解答】解:∵+|a﹣b|=0,
∴c2﹣a2﹣b2=0,且a﹣b=0,
∴c2=a2+b2,且a=b,
则△ABC为等腰直角三角形.
故答案为:等腰直角三角形
16.如图,在 ABCD中,AB=3,BC=5,对角线AC、BD相交于点O,过点O作OE⊥AC,交AD于点E,连接CE,则△CDE的周长为 8 .
【考点】线段垂直平分线的性质;平行四边形的性质.
【分析】根据平行四边形的性质,得知AO=OC,由于OE⊥AC,根据线段垂直平分线的性质,可知AE=EC,则△CDE的周长为CD与AD之和,即可得解.
【解答】解:根据平行四边形的性质,
∴AO=OC,
∵OE⊥AC,
∴OE为AC的垂直平分线,
∴AE=EC,
∴△CDE的周长为:CD+AD=5+3=8,
故答案为:8.
17.如图,D是△ABC内一点,BD⊥CD,AD=6,BD=4,CD=3,E、F、G、H分别是AB、AC、CD、BD的中点,则四边形EFGH的周长是 11 .
【考点】三角形中位线定理;勾股定理.
【分析】利用勾股定理列式求出BC的长,再根据三角形的中位线平行于第三边并且等于第三边的一半求出EH=FG=AD,EF=GH=BC,然后代入数据进行计算即可得解.
【解答】解:∵BD⊥CD,BD=4,CD=3,
∴BC===5,
∵E、F、G、H分别是AB、AC、CD、BD的中点,
∴EH=FG=AD,EF=GH=BC,
∴四边形EFGH的周长=EH+GH+FG+EF=AD+BC,
又∵AD=6,
∴四边形EFGH的周长=6+5=11.
故答案为:11.
18.如图,在边长为8的正方形ABCD中,E是AB边上的一点,且AE=6,点Q为对角线AC上的动点,则△BEQ周长的最小值为 12 .
【考点】正方形的性质;轴对称-最短路线问题.
【分析】连接BD,DE,根据正方形的性质可知点B与点D关于直线AC对称,故DE的长即为BQ+QE的最小值,进而可得出结论.
【解答】解:连接BD,DE,
∵四边形ABCD是正方形,
∴点B与点D关于直线AC对称,
∴DE的长即为BQ+QE的最小值,
∵AB=8,AE=6,
∴DE=BQ+QE==10,
∵AB=8,AE=6,
∴BE=2,
∴△BEQ周长的最小值=DE+BE=10+2=12.
故答案为:12.
三、解答题(7个小题,共66分)
19.(1)计算:
+|﹣2|+(﹣1)0﹣()﹣1
(2)先化简,再求值:(3x+2)(3x﹣2)﹣5x(x﹣1)﹣(2x﹣1)2,其中x=﹣.
【考点】整式的混合运算—化简求值;实数的运算;零指数幂;负整数指数幂.
【分析】(1)先根据二次根式的性质,绝对值,零指数幂,负整数指数幂分别求出每一部分的值,再代入求出即可;
(2)先算乘法,再合并同类项,最后代入求出即可.
【解答】解:(1)原式=2+2﹣﹣1﹣2
=﹣1;
(2)(3x+2)(3x﹣2)﹣5x(x﹣1)﹣(2x﹣1)2
=9x2﹣4﹣5x2+5x﹣4x2+4x﹣1
=9x﹣5,
当x=﹣,时,原式=9×(﹣)﹣5=﹣8.
20.图中方格纸中每个小正方形的边长都是1个单位长度,△ABC的位置如图所示.请在图中
(1)作出△A1B1C1,使其与△ABC关于点O成中心对称.
(2)作出△A2B2C2,使其与△ABC关于直线y成轴对称.
【考点】作图-旋转变换;作图-轴对称变换.
【分析】(1)作出各点关于原点的对称点,再顺次连接即可;
(2)作出各点关于y轴的对称点,再顺次连接即可.
【解答】解:(1)如图,△A1B1C1即为所求;
(2)如图,△A2B2C2即为所求.
21.如图,△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于E,D为垂足,连接EC.
(1)求∠ECD的度数;
(2)若CE=5,求BC长.
【考点】线段垂直平分线的性质;等腰三角形的性质.
【分析】(1)ED是AC的垂直平分线,可得AE=EC;∠A=∠C;已知∠A=36,即可求得;
(2)△ABC中,AB=AC,∠A=36°,可得∠B=72°又∠BEC=∠A+∠ECA=72°,所以,得BC=EC=5;
【解答】解:(1)∵DE垂直平分AC,
∴CE=AE,∴∠ECD=∠A=36°;
(2)∵AB=AC,∠A=36°,
∴∠B=∠ACB=72°,
∴∠BEC=∠A+∠ECD=72°,
∴∠BEC=∠B,
∴BC=EC=5.
答:(1)∠ECD的度数是36°;
(2)BC长是5.
22.如图,在Rt△ABC中,∠C=90°,BD是△ABC的一条角平分线.点O、E、F分别在BD、BC、AC上,且四边形OECF是正方形.
(1)求证:点O在∠BAC的平分线上;
(2)若AC=5,BC=12,求OE的长.
【考点】角平分线的性质;全等三角形的判定与性质;正方形的性质.
【分析】(1)过点O作OM⊥AB,由角平分线的性质得OE=OM,由正方形的性质得OE=OF,易得OM=OF,由角平分线的判定定理得点O在∠BAC的平分线上;
(2)由勾股定理得AB的长,利用方程思想解得结果.
【解答】(1)证明:过点O作OM⊥AB,
∵BD是∠ABC的一条角平分线,
∴OE=OM,
∵四边形OECF是正方形,
∴OE=OF,
∴OF=OM,
∴AO是∠BAC的角平分线,即点O在∠BAC的平分线上;
(2)解:∵在Rt△ABC中,AC=5,BC=12,
∴AB===13,
设CE=CF=x,BE=BM=y,AM=AF=z,
∴,
解得:,
∴CE=2,
∴OE=2.
23.如图,矩形ABCD中,点P是线段AD上一动点,O为BD的中点,PO的延长线交BC于Q.
(1)求证:OP=OQ;
(2)若AD=8厘米,AB=6厘米,P从点A出发,以1厘米/秒的速度向D运动(不与D重合).设点P运动时间为t秒,请用t表示PD的长;并求t为何值时,四边形PBQD是菱形.
【考点】相似三角形的判定与性质;全等三角形的判定与性质;勾股定理;菱形的性质;矩形的性质.
【分析】(1)本题需先根据四边形ABCD是矩形,得出AD∥BC,∠PDO=∠QBO,再根据O为BD的中点得出△POD≌△QOB,即可证出OP=OQ.
(2)本题需先根据已知条件得出∠A的度数,再根据AD=8厘米,AB=6厘米,得出BD和OD的长,再根据四边形PBQD是菱形时,即可求出t的值,判断出四边形PBQD是菱形.
【解答】(1)证明:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠PDO=∠QBO,
又∵O为BD的中点,
∴OB=OD,
在△POD与△QOB中,
∵
∴△POD≌△QOB(ASA),
∴OP=OQ;
(2)解:PD=8﹣t,
∵四边形PBQD是菱形,
∴PD=BP=8﹣t,
∵四边形ABCD是矩形,
∴∠A=90°,
在Rt△ABP中,由勾股定理得:AB2+AP2=BP2,
即62+t2=(8﹣t)2,
解得:t=,
即运动时间为秒时,四边形PBQD是菱形.
24.如图,在 ABCD中,F是AD的中点,延长BC到点E,使CE=BC,连接DE,CF.
(1)求证:四边形CEDF是平行四边形;
(2)若AB=4,AD=6,∠B=60°,求DE的长.
【考点】平行四边形的判定与性质;含30度角的直角三角形;勾股定理.
【分析】(1)由“平行四边形的对边平行且相等”的性质推知AD∥BC,且AD=BC;然后根据中点的定义、结合已知条件推知四边形CEDF的对边平行且相等(DF=CE,且DF∥CE),即四边形CEDF是平行四边形;
(2)如图,过点D作DH⊥BE于点H,构造含30度角的直角△DCH和直角△DHE.通过解直角△DCH和在直角△DHE中运用勾股定理来求线段ED的长度.
【解答】证明:(1)在 ABCD中,AD∥BC,且AD=BC.
∵F是AD的中点,
∴DF=.
又∵CE=BC,
∴DF=CE,且DF∥CE,
∴四边形CEDF是平行四边形;
(2)解:如图,过点D作DH⊥BE于点H.
在 ABCD中,∵∠B=60°,
∴∠DCE=60°.
∵AB=4,
∴CD=AB=4,
∴CH=CD=2,DH=2.
在 CEDF中,CE=DF=AD=3,则EH=1.
∴在Rt△DHE中,根据勾股定理知DE==.
25.如图,矩形ABCD中,AD=2AB,E是AD边上一点,DE=AD
(n为大于2的整数),连接BE,作BE的垂直平分线分别交AD、BC于点F,G,FG与BE的交点为O,连接BF和EG.
(1)试判断四边形BFEG的形状,并说明理由;
(2)当AB=4,n=3时,求FG的长;
(3)记四边形BFEG的面积为S1,矩形ABCD的面积为S2,当=时,求n的值.(直接写出结果,不必写出解答过程)
【考点】四边形综合题.
【分析】(1)先求证△EFO≌△BGO,可得EF=BG,再根据△BOF≌△EOF,可得EF=BF;即可证明四边形BFEG为菱形;
(2)根据菱形面积不同的计算公式(底乘高和对角线乘积的一半两种计算方式)可计算FG的长度;
(3)根据菱形面积底乘高的计算方式可以求出BG长度,根据勾股定理可求出AF的长度,即可求出ED的长度,即可计算n的值
【解答】解:(1)∵AD∥BC,
∴∠EFO=∠BGO,
∵FG为BE的垂直平分线,
∴BO=OE;
∵在△EFO和△BGO中,
,
∴△EFO≌△BGO,
∴EF=BG,
∵AD∥BC,
∴四边形BGEF为平行四边形,
∵FG是BE的垂直平分线,
∴FB=FE,
∴平行四边形BGEF为菱形;
(2)当AB=4,n=3时,
∴AD=8,AE=,
由勾股定理得,BE=,
AF=AE﹣EF=AE﹣BF,
在Rt△ABF中AB2+AF2=BF2,即(﹣BF)2+42=BF2,
解得,BF=,
则AF=,
菱形BGEF面积=BE FG=EF AB,即××FG=×4,
解得,FG=5;
(3)设AB=x,则DE=,
S1=BG AB,S2=BC AB
当=时,
=,
则BG=x,
在Rt△ABF中AB2+AF2=BF2,计算可得AF=x,
∴AE=AF+FE=AF+BG=x,DE=AD﹣AE=x,
∴x=,
∴n=6.
2016年11月2日
同课章节目录
