13.2.4 角边角课件
图片预览





文档简介
课件18张PPT。庙子一中 角边角2.基本事实:当两个三角形的两条边及其夹角分别对应相等时,两个三角形全等.(S.A.S.)注意:当两个三角形的两条边及其中一边的对角分别对应相等时,两个三角形不一定全等.
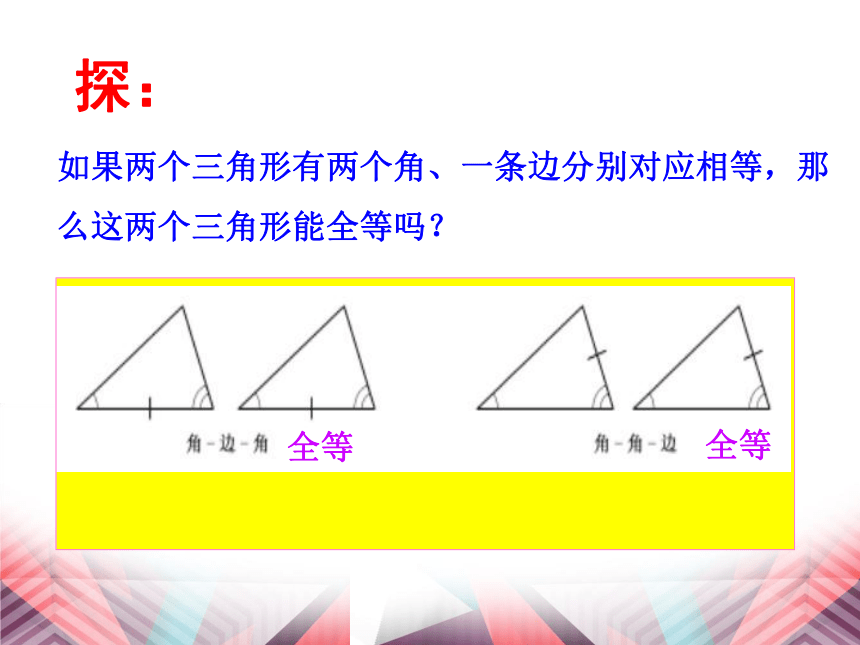
即没有S.S.A.你已经知道的判定三角形全等的方法有几种?1.根据三角形全等的定义. 小明踢球时不慎把一块三角形玻璃打碎为两块,他是否可以只带其中的一块碎片到商店去,就能配一块和原来一样的三角形玻璃呢?如果可以,带哪块去合适呢?为什么?(2)(1)疑:2.通过学习,进一步提高大家的推理论证能力.1.能够灵活运用“角边角”判定三角形全等,会用三角形全等的判定方法来证明简单的有关问题,并会进行有关计算.如果两个三角形有两个角、一条边分别对应相等,那么这两个三角形能全等吗?全等全等探:如图,已知两个角和一条线段,以这两个角为内角,以这条线段为这两个角的夹边,画一个三角形.60°40°4cmABC步骤:
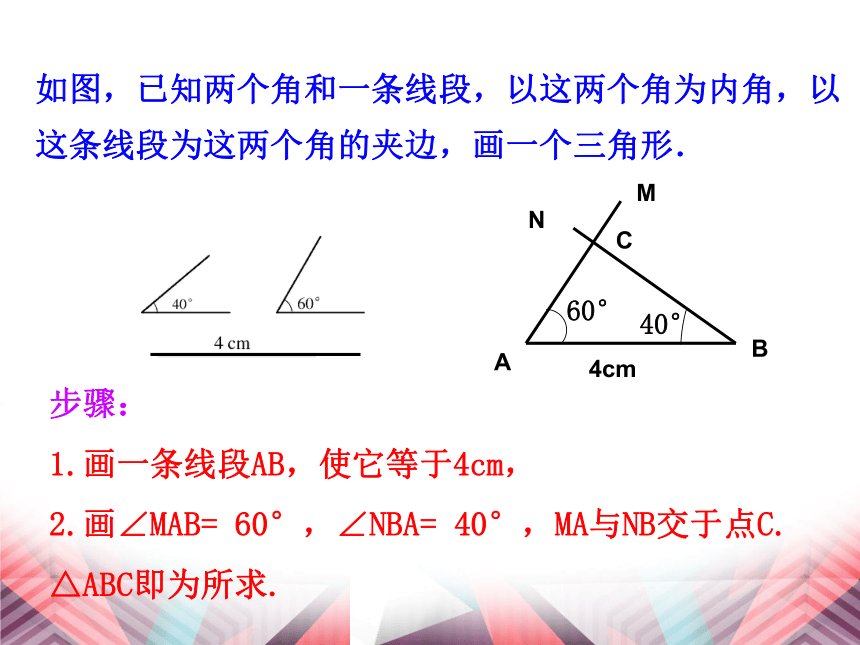
1.画一条线段AB,使它等于4cm,
2.画∠MAB= 60°,∠NBA= 40°,MA与NB交于点C.
△ABC即为所求.MN把你画的三角形与其他同学画的三角形
进行比较,所有的三角形都全等吗?
都全等在△ABC 与△A′B′C′中,若AB=A′B′, ∠A=∠A′, ∠B=∠B′,那么△ABC 与△A′B′C′全等吗?全等两角及其夹边分别相等的两个三角形全等.简记为A.S.A.(或角边角). 在△ABC和△DEF中,则△ABC≌△DEF.用符号语言表达为:∠B=∠E,
BC=EF,
∠C=∠F,基本事实如图,已知∠ABC=∠DCB,∠ACB=∠DBC,
求证:△ABC≌△DCB,AB=DC.∵∠ABC=∠DCB,
BC=CB,
∠ACB=∠DBC,证明:在△ABC和△DCB中,∴△ABC≌△DCB( ),
∴AB=DCA.S.A.【例题】1.已知:点D在AB上,点E在AC上,BE和CD相交于点O,AB=AC,∠B=∠C.
求证:△ABE≌△ACD.证明:在△ABE和△ACD中
∵ ∠A=∠A(公共角),
AB=AC(已知),
∠B=∠C(已知),
∴ △ABE≌△ACD(A.S.A.).OO展:1. 已知: △ABC和△ A′B′C′中,AB=A′B′, ∠A
=∠A′,∠B=∠B′, 则△ABC≌△ A′B′C′的根据是
( )
A.S.A.S. B.A.S.A. C.A.A.S. D.都不对B练:2.如图,△ABC是等腰三角形,AD、BE分别是∠BAC,
∠ABC的角平分线,△ABD和△BAE全等吗?试说明理由.解析 全等.∵ △ABC是等腰三角形
∴ ∠ABD=∠BAE.
∵ AD,BE分别是∠BAC,∠ABC
的角平分线,
∴ ∠BAD=∠ABE,
∵AB=BA
∴ △ABD≌△BAE(A.S.A.)通过本课时的学习,需要我们2.在判定三角形全等时,注意图形中的隐含条件.1.能够灵活运用“角边角”来判定三角形全等,会用三角形全等的判定方法来证明简单的有关问题,并会进行有关计算.1.如图,∠1=∠2,∠3=∠4,则
图中全等三角形的对数是( )
A. 3 B. 4
C. 5 D. 6
【解析】选D.共有6对,△ABD≌△CBD,△ABF≌△CBF,△ADE≌△CDE,△ABE≌△CBE,△AEF≌△CEF,△ADF≌△CDF.评:2.如图一,已知△ABC的边和角,则如图二所示,甲、乙、丙三个三角形中和△ABC全等的是( )
A. 甲和乙 B. 乙和丙
C. 甲和丙 D. 只有丙【解析】选B.图甲与已知图形只有一边、一角对应相等,不能判定两个三角形全等;图乙与已知图形满足两边及其夹角对应相等,符合“S.A.S.”条件,故两个三角形全等;图丙与已知图形满足两角及其中一角的对边对应相等,符合“A.A.S.”条件,故两个三角形全等.3.(武汉·中考)如图. 点B,
F,C,E在同一条直线上,点A,
D在直线BE的两侧,AB∥DE,
AC∥DF,BF=CE.
求证:AC=DF.
【证明】∵AB∥DE,∴∠B=∠E.
∵AC∥DF,∴∠ACB=∠DFE. ∵BF=CE,∴BC=EF.
∴△ABC≌△DEF(A.S.A.), ∴AC=DF.F
即没有S.S.A.你已经知道的判定三角形全等的方法有几种?1.根据三角形全等的定义. 小明踢球时不慎把一块三角形玻璃打碎为两块,他是否可以只带其中的一块碎片到商店去,就能配一块和原来一样的三角形玻璃呢?如果可以,带哪块去合适呢?为什么?(2)(1)疑:2.通过学习,进一步提高大家的推理论证能力.1.能够灵活运用“角边角”判定三角形全等,会用三角形全等的判定方法来证明简单的有关问题,并会进行有关计算.如果两个三角形有两个角、一条边分别对应相等,那么这两个三角形能全等吗?全等全等探:如图,已知两个角和一条线段,以这两个角为内角,以这条线段为这两个角的夹边,画一个三角形.60°40°4cmABC步骤:
1.画一条线段AB,使它等于4cm,
2.画∠MAB= 60°,∠NBA= 40°,MA与NB交于点C.
△ABC即为所求.MN把你画的三角形与其他同学画的三角形
进行比较,所有的三角形都全等吗?
都全等在△ABC 与△A′B′C′中,若AB=A′B′, ∠A=∠A′, ∠B=∠B′,那么△ABC 与△A′B′C′全等吗?全等两角及其夹边分别相等的两个三角形全等.简记为A.S.A.(或角边角). 在△ABC和△DEF中,则△ABC≌△DEF.用符号语言表达为:∠B=∠E,
BC=EF,
∠C=∠F,基本事实如图,已知∠ABC=∠DCB,∠ACB=∠DBC,
求证:△ABC≌△DCB,AB=DC.∵∠ABC=∠DCB,
BC=CB,
∠ACB=∠DBC,证明:在△ABC和△DCB中,∴△ABC≌△DCB( ),
∴AB=DCA.S.A.【例题】1.已知:点D在AB上,点E在AC上,BE和CD相交于点O,AB=AC,∠B=∠C.
求证:△ABE≌△ACD.证明:在△ABE和△ACD中
∵ ∠A=∠A(公共角),
AB=AC(已知),
∠B=∠C(已知),
∴ △ABE≌△ACD(A.S.A.).OO展:1. 已知: △ABC和△ A′B′C′中,AB=A′B′, ∠A
=∠A′,∠B=∠B′, 则△ABC≌△ A′B′C′的根据是
( )
A.S.A.S. B.A.S.A. C.A.A.S. D.都不对B练:2.如图,△ABC是等腰三角形,AD、BE分别是∠BAC,
∠ABC的角平分线,△ABD和△BAE全等吗?试说明理由.解析 全等.∵ △ABC是等腰三角形
∴ ∠ABD=∠BAE.
∵ AD,BE分别是∠BAC,∠ABC
的角平分线,
∴ ∠BAD=∠ABE,
∵AB=BA
∴ △ABD≌△BAE(A.S.A.)通过本课时的学习,需要我们2.在判定三角形全等时,注意图形中的隐含条件.1.能够灵活运用“角边角”来判定三角形全等,会用三角形全等的判定方法来证明简单的有关问题,并会进行有关计算.1.如图,∠1=∠2,∠3=∠4,则
图中全等三角形的对数是( )
A. 3 B. 4
C. 5 D. 6
【解析】选D.共有6对,△ABD≌△CBD,△ABF≌△CBF,△ADE≌△CDE,△ABE≌△CBE,△AEF≌△CEF,△ADF≌△CDF.评:2.如图一,已知△ABC的边和角,则如图二所示,甲、乙、丙三个三角形中和△ABC全等的是( )
A. 甲和乙 B. 乙和丙
C. 甲和丙 D. 只有丙【解析】选B.图甲与已知图形只有一边、一角对应相等,不能判定两个三角形全等;图乙与已知图形满足两边及其夹角对应相等,符合“S.A.S.”条件,故两个三角形全等;图丙与已知图形满足两角及其中一角的对边对应相等,符合“A.A.S.”条件,故两个三角形全等.3.(武汉·中考)如图. 点B,
F,C,E在同一条直线上,点A,
D在直线BE的两侧,AB∥DE,
AC∥DF,BF=CE.
求证:AC=DF.
【证明】∵AB∥DE,∴∠B=∠E.
∵AC∥DF,∴∠ACB=∠DFE. ∵BF=CE,∴BC=EF.
∴△ABC≌△DEF(A.S.A.), ∴AC=DF.F
