四川省成都市新都一中高中数学选修2-1第二章圆锥曲线与方程10抛物线的简单几何性质 (共36张PPT)
文档属性
| 名称 | 四川省成都市新都一中高中数学选修2-1第二章圆锥曲线与方程10抛物线的简单几何性质 (共36张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-11-03 09:27:32 | ||
图片预览











文档简介
课件36张PPT。高中数学人教A版
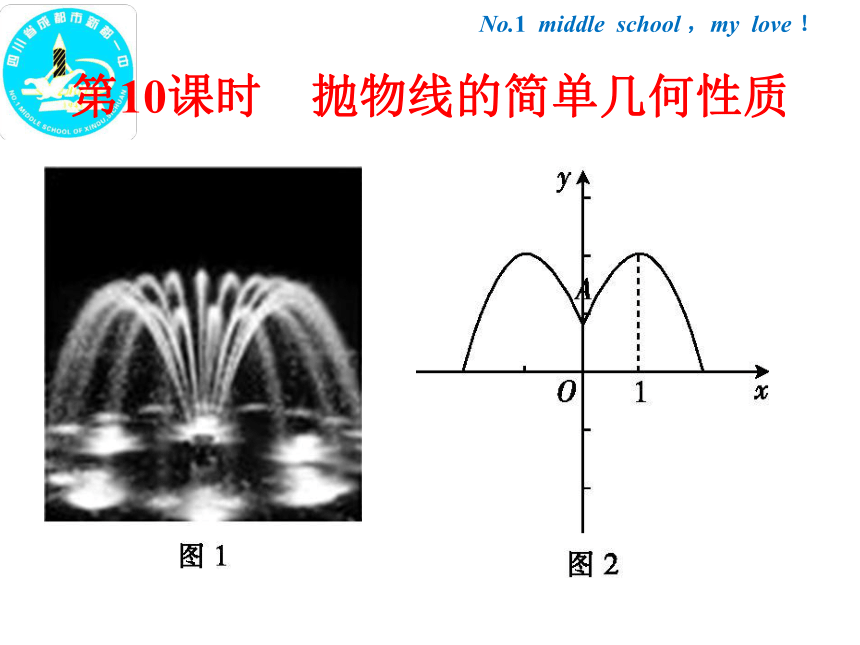
选修2-1No.1 middle school ,my love !某公园要建造一个如图1的圆形喷水池,在水池中央垂直于水面安装一个花形柱子OA,O恰在水面中心,OA=0.81米,安置在柱子顶端A处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,且在过OA的任一平面上抛物线路径如图2所示.为使水流形状较为漂亮,设计成水流在与OA距离为1米处达到距水面最大高度2.25米.No.1 middle school ,my love !第10课时 抛物线的简单几何性质No.1 middle school ,my love !第10课时 抛物线的简单几何性质预学1:在上述情境中,如果不计其他因素,那么水池的半径至少要2.25米,才能使喷出的水流不致落到池外.
议一议:影响抛物线开口大小的量是什么?是如何影响的?(抢答)
【解析】影响抛物线开口大小的量是参数p.p值越大,抛物线的开口越开阔,反之,开口越扁狭.No.1 middle school ,my love !第10课时 抛物线的简单几何性质预学2:抛物线y2=2px(p>0)的一些简单几何性质
(1)范围:因为p>0,由方程y2=2px可知,这条抛物线上任意一点M的坐标(x,y)满足等式.所以这条抛物线在y轴的右侧;当x的值增大时,|y|也增大,这说明抛物线向右上方和右下方无限延伸,它开口越开阔.No.1 middle school ,my love !第10课时 抛物线的简单几何性质(2)对称性:以-y代y,方程y2=2px(p>0)不变,因此这条抛物线是以x轴为对称轴的轴对称图形,抛物线的对称轴叫作抛物线的轴.
(3)顶点:抛物线和它的轴的交点叫作抛物线的顶点.在方程y2=2px(p>0)中,当y=0时,x=0,因此这条抛物线的顶点就是坐标原点.
(4)离心率:抛物线上的点与焦点和准线的距离的比,叫作抛物线的离心率,用e表示,按照抛物线的定义,e=1.No.1 middle school ,my love !第10课时 抛物线的简单几何性质(5)通径:过抛物线的焦点且垂直于抛物线对称轴的一条弦,称为抛物线的通径,通径长为2p,且通径是所有过焦点的弦中的最短弦.
议一议:抛物线x2=2py(p>0)有几条对称轴?是否是中心对称图形?(指定小组回答,其他组补充)
【解析】有一条对称轴,即y轴,不是中心对称图形.No.1 middle school ,my love !第10课时 抛物线的简单几何性质?No.1 middle school ,my love !第10课时 抛物线的简单几何性质【解析】由抛物线y2=8x的焦点为(2,0),得直线的方程为y=x-2.
代入y2=8x,得(x-2)2=8x,
即x2-12x+4=0.
所以x1+x2=12,
弦长=x1+x2+p=12+4=16.
【答案】16No.1 middle school ,my love !第10课时 抛物线的简单几何性质预学4:常见的与抛物线有关的最值问题的题型及解题方法
(1)题型:求抛物线上一点到定直线的最小距离;求抛物线上一点到定点的最值问题.No.1 middle school ,my love !第10课时 抛物线的简单几何性质?No.1 middle school ,my love !第10课时 抛物线的简单几何性质?No.1 middle school ,my love !第10课时 抛物线的简单几何性质?No.1 middle school ,my love !第10课时 抛物线的简单几何性质1.由抛物线的几何性质求标准方程
例1顶点在原点,对称轴是y轴,并且顶点与焦点的距离等于3的抛物线的标准方程是( ).
A.x2=±3y B.y2=±6x
C.x2=±12y D.x2=±6y
【方法指导】题中的焦点位置不明确,需分焦点在y轴的正负两个半轴上分别求解.No.1 middle school ,my love !第10课时 抛物线的简单几何性质?No.1 middle school ,my love !第10课时 抛物线的简单几何性质?No.1 middle school ,my love !第10课时 抛物线的简单几何性质【方法指导】(1)求抛物线上的一点到已知直线的距离最短的解题思路一般有三种方法:①构造函数法;②数形结合法;③转化法.
(2)以原点为一个顶点的三角形的“四心”在抛物线的对称轴上,另两个顶点必定关于对称轴对称.No.1 middle school ,my love !第10课时 抛物线的简单几何性质?No.1 middle school ,my love !第10课时 抛物线的简单几何性质?No.1 middle school ,my love !第10课时 抛物线的简单几何性质?No.1 middle school ,my love !第10课时 抛物线的简单几何性质3.抛物线的实际应用
例3某大桥在涨水时有最大跨度的中央桥孔,已知上部呈抛物线形,跨度为20米,拱顶距水面6米,桥墩高出水面4米.现有一货船欲过此孔,该货船水下宽度不超过18米,目前吃水线上部分中央船体高5米,宽16米,且该货船在现在状况下还可多装1000吨货物,但每多装150吨货物,船体吃水线就要上升0.04米,若不考虑水下深度,问:该货船在现在状况下能否直接或设法通过该桥孔?为什么?No.1 middle school ,my love !第10课时 抛物线的简单几何性质【方法指导】分析题意,建立平面直角坐标系,设出抛物线标准方程,确定点的坐标求p,利用方程求值,回答实际问题.
【解析】如图所示,以拱顶为原点,过拱顶的水平直线为x轴,竖直直线为y轴,建立平面直角坐标系.No.1 middle school ,my love !第10课时 抛物线的简单几何性质?No.1 middle school ,my love !第10课时 抛物线的简单几何性质此时B点距水面6+(-1.28)=4.72(米).
而船体高为5米,∴无法通行.
又∵5-4.72=0.28(米),0.28÷0.04=7,
150×7=1050(吨),
即若船通过增加货物通过桥孔,则要增加1050吨,而船最多还能装1000吨货物,∴通过增加货物也无法通行.
∴只好等待水位下降船才能通过该桥孔.No.1 middle school ,my love !第10课时 抛物线的简单几何性质变式训练1、等腰直角三角形的直角顶点位于坐标原点,另外两个顶点在抛物线y2=2px(p>0)上.若该三角形的斜边长为4,求此抛物线的方程.
【解析】如图,设等腰直角三角形 OAB的顶点A,B在抛物线上.
根据抛物线的性质知A,B关于x轴对称.
由题意得A(2,2)在抛物线y2=2px上,
所以p=1,抛物线的方程为y2=2x.No.1 middle school ,my love !第10课时 抛物线的简单几何性质?No.1 middle school ,my love !第10课时 抛物线的简单几何性质变式训练3、一条隧道的横断面由抛物线弧及一个矩形的三条边围成,尺寸如右图所示(单位:m),一辆卡车空车时能通过此隧道,现载一集装箱,箱宽3 m,车与箱共高4.5 m,此车能否通过隧道?并说明理由.No.1 middle school ,my love !第10课时 抛物线的简单几何性质?No.1 middle school ,my love !第10课时 抛物线的简单几何性质?No.1 middle school ,my love !第10课时 抛物线的简单几何性质No.1 middle school ,my love !第10课时 抛物线的简单几何性质1.用待定系数法求抛物线标准方程的步骤:No.1 middle school ,my love !第10课时 抛物线的简单几何性质2.研究抛物线的几何性质时,一是注意定义转化应用;二是要结合图形分析,同时注意平面几何性质的应用.
3.涉及桥的高度、隧道的高低等问题,通常用抛物线的标准方程解决,建立平面直角坐标系后,要注意点的坐标有正负之分,与实际问题中的数据并不完全相同.?No.1 middle school ,my love !第10课时 抛物线的简单几何性质No.1 middle school ,my love !第10课时 抛物线的简单几何性质 1.抛物线的焦点及开口方向No.1 middle school ,my love !第10课时 抛物线的简单几何性质2.抛物线的主要性质及应用方向No.1 middle school ,my love !作业:见固学案第10课时 抛物线的简单几何性质Thanks2016年11月2日No.1 middle school ,my love !
议一议:影响抛物线开口大小的量是什么?是如何影响的?(抢答)
【解析】影响抛物线开口大小的量是参数p.p值越大,抛物线的开口越开阔,反之,开口越扁狭.No.1 middle school ,my love !第10课时 抛物线的简单几何性质预学2:抛物线y2=2px(p>0)的一些简单几何性质
(1)范围:因为p>0,由方程y2=2px可知,这条抛物线上任意一点M的坐标(x,y)满足等式.所以这条抛物线在y轴的右侧;当x的值增大时,|y|也增大,这说明抛物线向右上方和右下方无限延伸,它开口越开阔.No.1 middle school ,my love !第10课时 抛物线的简单几何性质(2)对称性:以-y代y,方程y2=2px(p>0)不变,因此这条抛物线是以x轴为对称轴的轴对称图形,抛物线的对称轴叫作抛物线的轴.
(3)顶点:抛物线和它的轴的交点叫作抛物线的顶点.在方程y2=2px(p>0)中,当y=0时,x=0,因此这条抛物线的顶点就是坐标原点.
(4)离心率:抛物线上的点与焦点和准线的距离的比,叫作抛物线的离心率,用e表示,按照抛物线的定义,e=1.No.1 middle school ,my love !第10课时 抛物线的简单几何性质(5)通径:过抛物线的焦点且垂直于抛物线对称轴的一条弦,称为抛物线的通径,通径长为2p,且通径是所有过焦点的弦中的最短弦.
议一议:抛物线x2=2py(p>0)有几条对称轴?是否是中心对称图形?(指定小组回答,其他组补充)
【解析】有一条对称轴,即y轴,不是中心对称图形.No.1 middle school ,my love !第10课时 抛物线的简单几何性质?No.1 middle school ,my love !第10课时 抛物线的简单几何性质【解析】由抛物线y2=8x的焦点为(2,0),得直线的方程为y=x-2.
代入y2=8x,得(x-2)2=8x,
即x2-12x+4=0.
所以x1+x2=12,
弦长=x1+x2+p=12+4=16.
【答案】16No.1 middle school ,my love !第10课时 抛物线的简单几何性质预学4:常见的与抛物线有关的最值问题的题型及解题方法
(1)题型:求抛物线上一点到定直线的最小距离;求抛物线上一点到定点的最值问题.No.1 middle school ,my love !第10课时 抛物线的简单几何性质?No.1 middle school ,my love !第10课时 抛物线的简单几何性质?No.1 middle school ,my love !第10课时 抛物线的简单几何性质?No.1 middle school ,my love !第10课时 抛物线的简单几何性质1.由抛物线的几何性质求标准方程
例1顶点在原点,对称轴是y轴,并且顶点与焦点的距离等于3的抛物线的标准方程是( ).
A.x2=±3y B.y2=±6x
C.x2=±12y D.x2=±6y
【方法指导】题中的焦点位置不明确,需分焦点在y轴的正负两个半轴上分别求解.No.1 middle school ,my love !第10课时 抛物线的简单几何性质?No.1 middle school ,my love !第10课时 抛物线的简单几何性质?No.1 middle school ,my love !第10课时 抛物线的简单几何性质【方法指导】(1)求抛物线上的一点到已知直线的距离最短的解题思路一般有三种方法:①构造函数法;②数形结合法;③转化法.
(2)以原点为一个顶点的三角形的“四心”在抛物线的对称轴上,另两个顶点必定关于对称轴对称.No.1 middle school ,my love !第10课时 抛物线的简单几何性质?No.1 middle school ,my love !第10课时 抛物线的简单几何性质?No.1 middle school ,my love !第10课时 抛物线的简单几何性质?No.1 middle school ,my love !第10课时 抛物线的简单几何性质3.抛物线的实际应用
例3某大桥在涨水时有最大跨度的中央桥孔,已知上部呈抛物线形,跨度为20米,拱顶距水面6米,桥墩高出水面4米.现有一货船欲过此孔,该货船水下宽度不超过18米,目前吃水线上部分中央船体高5米,宽16米,且该货船在现在状况下还可多装1000吨货物,但每多装150吨货物,船体吃水线就要上升0.04米,若不考虑水下深度,问:该货船在现在状况下能否直接或设法通过该桥孔?为什么?No.1 middle school ,my love !第10课时 抛物线的简单几何性质【方法指导】分析题意,建立平面直角坐标系,设出抛物线标准方程,确定点的坐标求p,利用方程求值,回答实际问题.
【解析】如图所示,以拱顶为原点,过拱顶的水平直线为x轴,竖直直线为y轴,建立平面直角坐标系.No.1 middle school ,my love !第10课时 抛物线的简单几何性质?No.1 middle school ,my love !第10课时 抛物线的简单几何性质此时B点距水面6+(-1.28)=4.72(米).
而船体高为5米,∴无法通行.
又∵5-4.72=0.28(米),0.28÷0.04=7,
150×7=1050(吨),
即若船通过增加货物通过桥孔,则要增加1050吨,而船最多还能装1000吨货物,∴通过增加货物也无法通行.
∴只好等待水位下降船才能通过该桥孔.No.1 middle school ,my love !第10课时 抛物线的简单几何性质变式训练1、等腰直角三角形的直角顶点位于坐标原点,另外两个顶点在抛物线y2=2px(p>0)上.若该三角形的斜边长为4,求此抛物线的方程.
【解析】如图,设等腰直角三角形 OAB的顶点A,B在抛物线上.
根据抛物线的性质知A,B关于x轴对称.
由题意得A(2,2)在抛物线y2=2px上,
所以p=1,抛物线的方程为y2=2x.No.1 middle school ,my love !第10课时 抛物线的简单几何性质?No.1 middle school ,my love !第10课时 抛物线的简单几何性质变式训练3、一条隧道的横断面由抛物线弧及一个矩形的三条边围成,尺寸如右图所示(单位:m),一辆卡车空车时能通过此隧道,现载一集装箱,箱宽3 m,车与箱共高4.5 m,此车能否通过隧道?并说明理由.No.1 middle school ,my love !第10课时 抛物线的简单几何性质?No.1 middle school ,my love !第10课时 抛物线的简单几何性质?No.1 middle school ,my love !第10课时 抛物线的简单几何性质No.1 middle school ,my love !第10课时 抛物线的简单几何性质1.用待定系数法求抛物线标准方程的步骤:No.1 middle school ,my love !第10课时 抛物线的简单几何性质2.研究抛物线的几何性质时,一是注意定义转化应用;二是要结合图形分析,同时注意平面几何性质的应用.
3.涉及桥的高度、隧道的高低等问题,通常用抛物线的标准方程解决,建立平面直角坐标系后,要注意点的坐标有正负之分,与实际问题中的数据并不完全相同.?No.1 middle school ,my love !第10课时 抛物线的简单几何性质No.1 middle school ,my love !第10课时 抛物线的简单几何性质 1.抛物线的焦点及开口方向No.1 middle school ,my love !第10课时 抛物线的简单几何性质2.抛物线的主要性质及应用方向No.1 middle school ,my love !作业:见固学案第10课时 抛物线的简单几何性质Thanks2016年11月2日No.1 middle school ,my love !
