三角形探索三角形全等的条件

课件22张PPT。复兴学校 罗燕秋第四节 探索三角形全等的条件(一)北师大版七年级数学下册1、通过探索三角形全等的过程，体会数学思维的严密性。
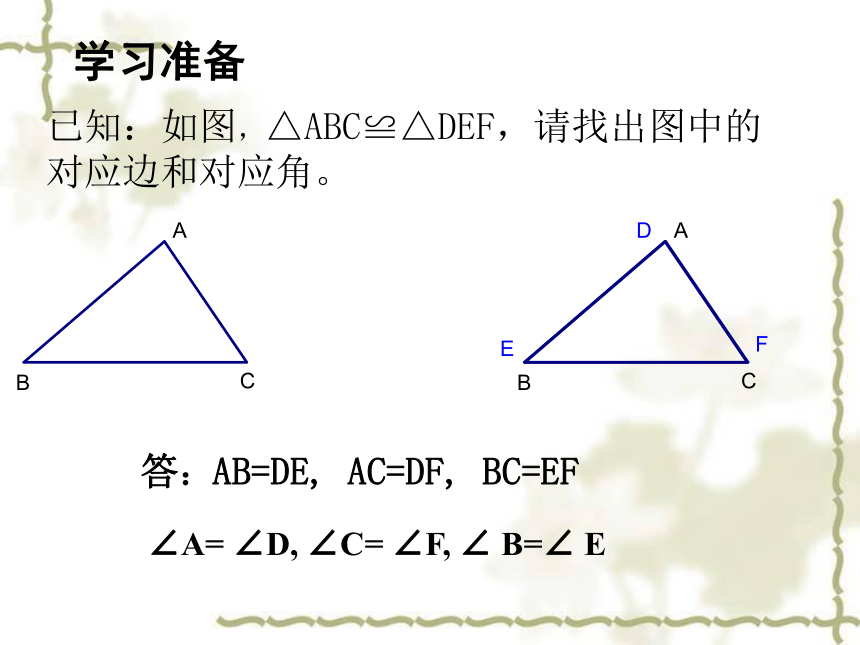
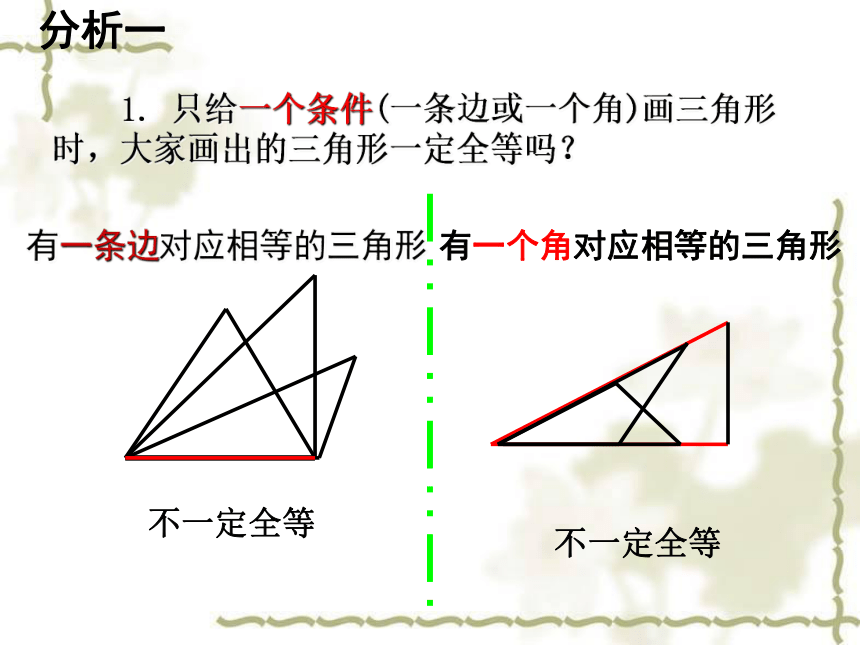
学习目标2、了解三角形的稳定性和实际生活的例子。3、理解并且会用三角形全等的“边边边”条件。学习重点：用 “边边边”判定三角形全等。学习难点：三角形全等条件的探索。已知：如图，△ABC≌△DEF，请找出图中的对应边和对应角。答：AB=DE, AC=DF, BC=EF∠A= ∠D, ∠C= ∠F, ∠ B=∠ E学习准备要画一个三角形与老师画的三角形全等，需要几个与边或角的大小有关的条件呢？新知探索分析一 1. 只给一个条件(一条边或一个角)画三角形时，大家画出的三角形一定全等吗？有一条边对应相等的三角形不一定全等有一个角对应相等的三角形不一定全等分析二若给出两个条件画三角形，你能说出有哪几中可能情况?一个角，一条边
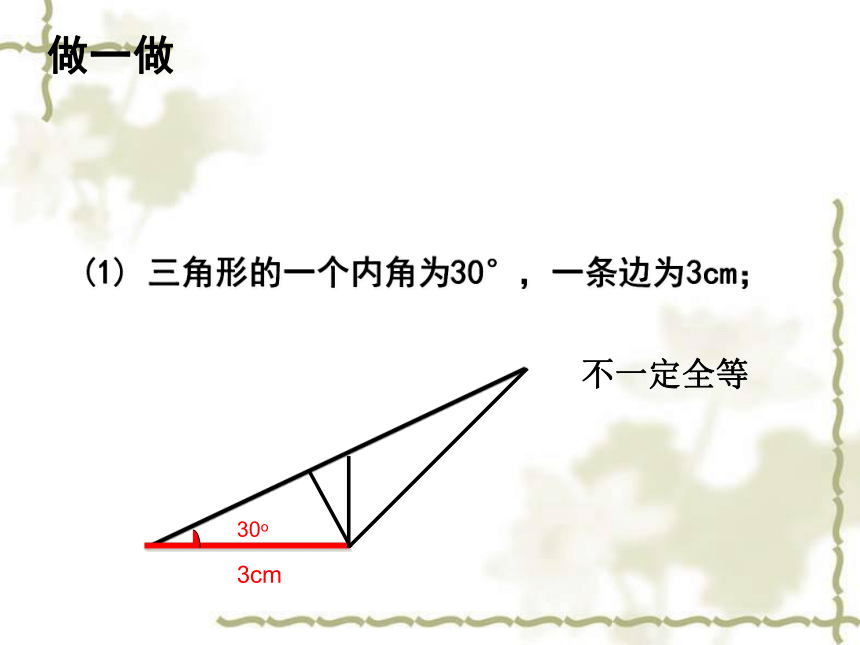
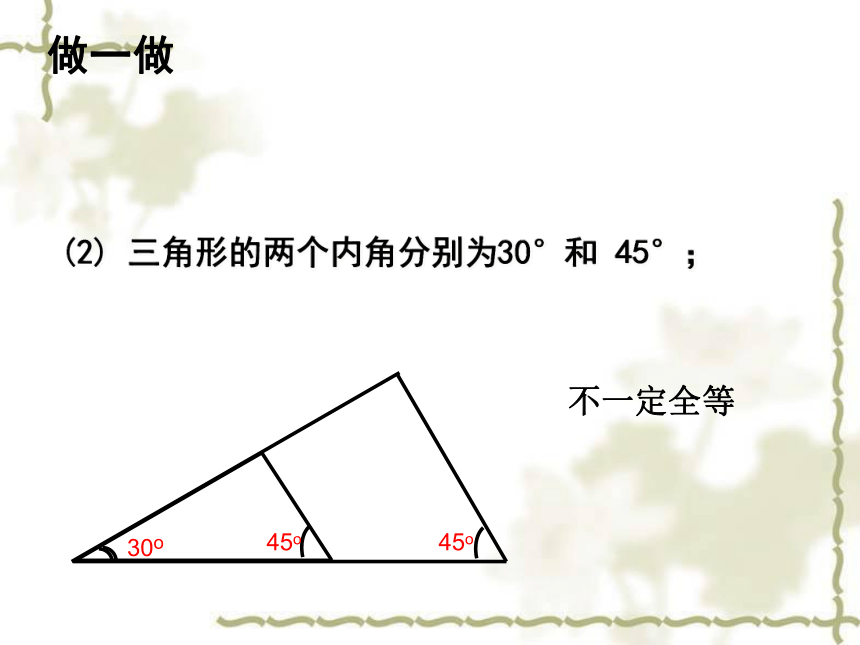
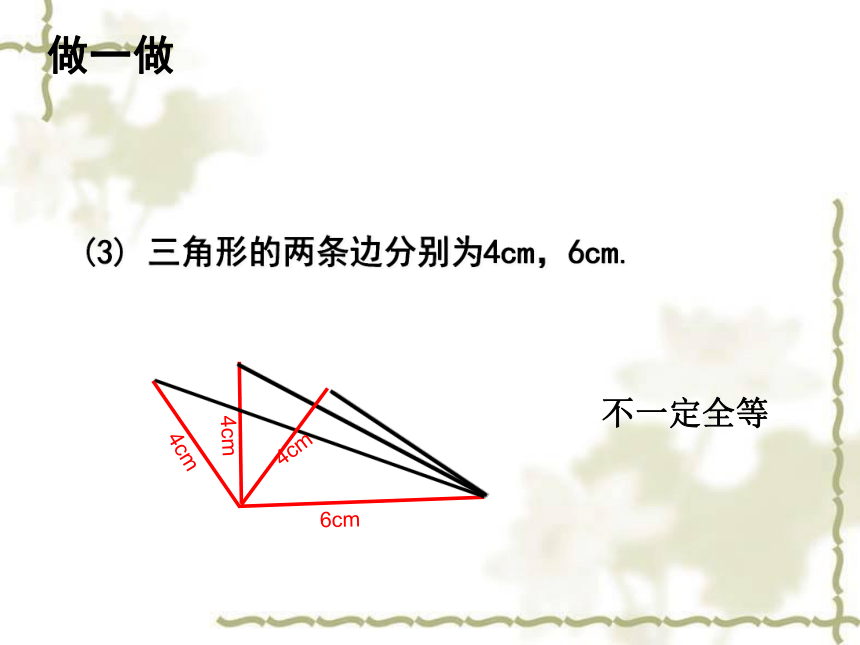
2. 两个都是角3.两个都是边做一做(1) 三角形的一个内角为30°，一条边为3cm；不一定全等做一做(2) 三角形的两个内角分别为30°和 45°；30o不一定全等45o45o做一做(3) 三角形的两条边分别为4cm，6cm.4cm6cm不一定全等分析三若给出三个条件画三角形，你能说出有哪几中可能情况?都给角：给三个角
2. 都给边：给三条边3.既给角，又给边：给两条边，一个角给一条边，两个角（1）（2）已知一个三角形的三个内角 分别为300，600，900，请画出这个三角形。结论：三个内角对应相等的两个三角形不一定全等.1.给出三个角已知三角形的三条边分 别为4cm、5cm和7cm，
请画出这个三角形。三边对应相等的两个三角形全等，
简写为“边边边”或“SSS”边边边公理：2.给出三条边三边对应相等的两个三角形全等，简写为“边边边”或“SSS”。在△ABC和△DEF中∴ △ABC≌△DEF（SSS）动脑想一想准备若干长度适中的小木条，用其中三根木条钉成一个三角形的框架，它的形状和大小是固定的吗？如果用四根小木条钉成的框架形状和大小固定吗？三角形的框架，它的大小和形状是固定不变的，三角形的这个性质叫做三角形的稳定性。生活中的具体应用例1 如图，当 AB=CD，BC=DA时，图中的△ABC与△CDA是否全等？并说明理由。答:△ABC与△CDA是全等三角形。理由是：在△ABC与△CDA中∴△ABC≌△CDA（SSS）∵AB=CDAD=CBAC=CA(已知)(已知)(公共边)例题赏析已知：AC、BD相交于点O，且AB=DC，AC=DB，那么∠A=∠D吗？为什么？答： 我认为：∠A=∠D证明：在△ABC和△DCB中∵∴△ABC≌△DCB （SSS）∴∠A=∠D（全等三角形的对应角相等）练习∴∠3=∠4， ∠1=∠2 (全等三角形对应角相等）答：能判定AB∥CD.
∴AB∥CD， AD∥BC （内错角相等，两直线平行）变式 如图，当 AB=CD，BC=DA时，你能说明AB与CD、AD与BC的位置关系吗？为什么？证明：在△ABC与△CDA中∴△ABC≌△CDA（SSS）∵AB=CDAD=CBAC=CA(已知)(已知)(公共边)1234举一反三已知：如图，AB=DE, BC=EF, AF=CD.
(1) △ABC与△DEF是否全等？并说明理由。
(2) 求证：∠A=∠D证明:( SSS)∴ ∠A=∠D(全等三角形的对应角相等)答：我认为：△ABC≌△DEF∵AF = DC（已知）∴AF+FC= DC+FC（等式的性质）在△ABC和△DEF中∵AB = DE（已知）BC = EF（已知）AC = DF（已证）∴△ABC≌△DEF即AC=DF思考题小结：
　　今天我们经历了画图验证两个三角形全等的过程，探索出两个三角形全等的条件之一“三边对应相等的两个三角形全等”，我们可以利用它来判别两个三角形是否全等。 我们还知道了三角形具有稳定性，只要三角形的三边长度确定了，这个三角形的形状和大小就确定了。在生活中，三角形的稳定性有广泛的应用。作业：
P160页习题5.7
数学理解:第1、2题
问题解决:第1题