第十三章 全等三角形 线段垂直平分线与角平分线 专题训练题 含答案
文档属性
| 名称 | 第十三章 全等三角形 线段垂直平分线与角平分线 专题训练题 含答案 |
|
|
| 格式 | zip | ||
| 文件大小 | 241.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-11-03 07:52:21 | ||
图片预览


文档简介
华东师大版数学八年级上册
第十三章
全等三角形
线段垂直平分线与角平分线
专题训练题
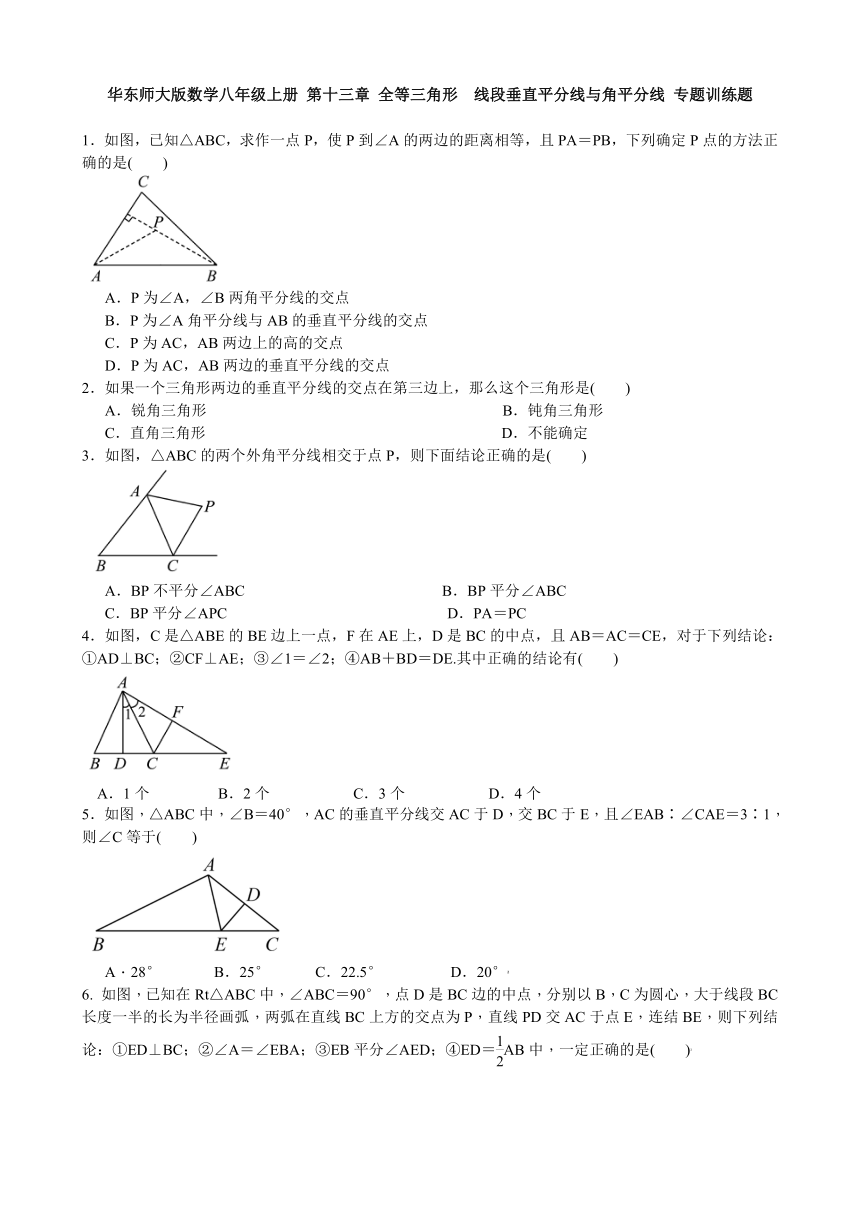
1.如图,已知△ABC,求作一点P,使P到∠A的两边的距离相等,且PA=PB,下列确定P点的方法正确的是( )
A.P为∠A,∠B两角平分线的交点
B.P为∠A角平分线与AB的垂直平分线的交点
C.P为AC,AB两边上的高的交点
D.P为AC,AB两边的垂直平分线的交点
2.如果一个三角形两边的垂直平分线的交点在第三边上,那么这个三角形是( )
A.锐角三角形
B.钝角三角形
C.直角三角形
D.不能确定
3.如图,△ABC的两个外角平分线相交于点P,则下面结论正确的是( )
A.BP不平分∠ABC
B.BP平分∠ABC
C.BP平分∠APC
D.PA=PC
4.如图,C是△ABE的BE边上一点,F在AE上,D是BC的中点,且AB=AC=CE,对于下列结论:①AD⊥BC;②CF⊥AE;③∠1=∠2;④AB+BD=DE.其中正确的结论有( )
A.1个
B.2个
C.3个
D.4个
5.如图,△ABC中,∠B=40°,AC的垂直平分线交AC于D,交BC于E,且∠EAB∶∠CAE=3∶1,则∠C等于( )
A.28°
B.25°
C.22.5°
D.20°24
6.
如图,已知在Rt△ABC中,∠ABC=90°,点D是BC边的中点,分别以B,C为圆心,大于线段BC长度一半的长为半径画弧,两弧在直线BC上方的交点为P,直线PD交AC于点E,连结BE,则下列结论:①ED⊥BC;②∠A=∠EBA;③EB平分∠AED;④ED=AB中,一定正确的是( )3
A.①②③
B.①②④
C.①③④
D.②③④C
7.
如图,在△ABC中,∠ABC=50°,∠ACB=60°,点E在BC的延长线上,∠ABC的平分线BD与∠ACE的平分线CD相交于点D,连结AD,下列结论中不正确的是( )
Y
A.∠BAC=70°
B.∠DOC=90°
I
C.∠BDC=35°
D.∠DAC=55°4
8.如图所示,在△ABC中,∠C=90°,DE是AB的垂直平分线,∠BAD∶∠BAC=1∶3,则∠B=______.C
9.如图,在△ABC中,AD是它的角平分线,AB=6
cm,AC=8
cm,则S△ABD∶S△ACD=________,BD∶CD=________.f
10.如图,已知BD⊥AN于B,交AE于点O,OC⊥AM于点C,且OB=OC,如果∠OAB=25°,则∠ADB=________.e
11.如图,∠AOB内有点P,P1,P2分别是P关于OA,OB的对称点,P1P2交OA于M,交OB于N,若P1P2=5
cm,则△PMN的周长为________cm.o
12.如图,BD是∠ABC的角平分线,DE⊥AB于E,DF⊥BC于F,S△ABC=45
cm2,AB=12
cm,BC=18
cm,则DE的长是________.V
13.如图,已知:CD⊥AB于D,BE⊥AC于E,且BD=CE,BE交CD于点O.求证:AO平分∠BAC.E
14.如图所示,点P在线段AB的垂直平分线上,PC⊥PA,PD⊥PB,AC=BD,求证:点P在线段CD的垂直平分线上.
L
15.已知如图,AD是∠BAC的角平分线,DE⊥AB,DF⊥AC,垂足分别是E,F.k
求证:AD垂直平分EF.g
16.如图,在△ABC中,∠ACB=90°,CE⊥AB于点E,AD=AC,AF平分∠CAB交CE于点F,DF的延长线交AC于点G,试问:B4587478
(1)DF与BC有何位置关系?请说明理由;/
(2)FG与FE有何数量关系?请证明你的结论./
17.如图,△OBC中,BC的垂直平分线DP交∠BOC的平分线于D,垂足为P.V
(1)若∠BOC=60°,求∠BDC的度数;P
(2)若∠BOC=α,则∠BDC=________(直接写出结果).x4587478
答案:4587478
1---5
BCBBA
6.
B
7.
Bc
8.
22.5°Q
9.
3∶4
3∶4=
10.
40°=
11.
5
12.
3cm
13.
∵OD⊥AB,OE⊥AC,∴∠BDO=∠CEO=90°,又∵∠BOD=∠COE,BD=CE,∴△BOD≌△COE,∴OD=OE,又由已知条件得△AOD和△AOE都是直角三角形,且OD=OE,OA=OA,∴Rt△AOD≌Rt△AOE,∴∠DAO=∠EAO,即AO平分∠BAC
14.
∵点P在AB的垂直平分线上,∴PA=PB,∵PC⊥PA,PD⊥PB,∴∠BPD=∠APC=90°,又AC=BD,∴Rt△APC≌Rt△BPD(H.L.),∴PD=PC,∴点P在线段CD的垂直平分线上
15.
∵AD是∠BAC的角平分线,DE⊥AB,DF⊥AC,∴DE=DF,∴∠1=∠2,∵∠AED=∠AFD=90°,∴∠3=∠4,∴AE=AF,∵AD是等腰三角形AEF的顶角平分线,∴AD垂直平分EF(三线合一)
16.
(1)DF∥BC,理由是:∵AF平分∠BAC,∴∠CAF=∠DAF,在△CAF和△DAF中,,∴△CAF≌△DAF(S.A.S.),∴∠ADF=∠ACF,∵CE⊥AB,∠ACB=90°,∴∠CEB=∠ACB=90°,∴∠ACF+∠BCF=90°,∠B+∠BCF=90°,∴∠B=∠ACF=∠ADF,∴DF∥BC
(2)FG=EF,证明:∵DF∥BC,∠ACB=90°,∴∠AGF=∠ACB=90°,∴FG⊥AC,又∵CE⊥AB,AF平分∠CAB,∴FG=EF
17.
(1)过点D作DE⊥OB,交OB延长线于点E,DF⊥OC于F,∵OD是∠BOC的平分线,∴DE=DF,∵DP是BC的垂直平分线,∴BD=CD,在Rt△DEB和Rt△DFC中,,∴△DEB≌△DFC(H.L.),∴∠BDE=∠CDF,∴∠BDC=∠EDF,∵∠EOF+[JP]∠EDF=180°,∠BOC=60°,∴∠BDC=∠EDF=120°
(2)∵∠EOF+∠EDF=180°,∠BOC=α,∴∠BDC=∠EDF=180°-α.故答案为:180°-α
第十三章
全等三角形
线段垂直平分线与角平分线
专题训练题
1.如图,已知△ABC,求作一点P,使P到∠A的两边的距离相等,且PA=PB,下列确定P点的方法正确的是( )
A.P为∠A,∠B两角平分线的交点
B.P为∠A角平分线与AB的垂直平分线的交点
C.P为AC,AB两边上的高的交点
D.P为AC,AB两边的垂直平分线的交点
2.如果一个三角形两边的垂直平分线的交点在第三边上,那么这个三角形是( )
A.锐角三角形
B.钝角三角形
C.直角三角形
D.不能确定
3.如图,△ABC的两个外角平分线相交于点P,则下面结论正确的是( )
A.BP不平分∠ABC
B.BP平分∠ABC
C.BP平分∠APC
D.PA=PC
4.如图,C是△ABE的BE边上一点,F在AE上,D是BC的中点,且AB=AC=CE,对于下列结论:①AD⊥BC;②CF⊥AE;③∠1=∠2;④AB+BD=DE.其中正确的结论有( )
A.1个
B.2个
C.3个
D.4个
5.如图,△ABC中,∠B=40°,AC的垂直平分线交AC于D,交BC于E,且∠EAB∶∠CAE=3∶1,则∠C等于( )
A.28°
B.25°
C.22.5°
D.20°24
6.
如图,已知在Rt△ABC中,∠ABC=90°,点D是BC边的中点,分别以B,C为圆心,大于线段BC长度一半的长为半径画弧,两弧在直线BC上方的交点为P,直线PD交AC于点E,连结BE,则下列结论:①ED⊥BC;②∠A=∠EBA;③EB平分∠AED;④ED=AB中,一定正确的是( )3
A.①②③
B.①②④
C.①③④
D.②③④C
7.
如图,在△ABC中,∠ABC=50°,∠ACB=60°,点E在BC的延长线上,∠ABC的平分线BD与∠ACE的平分线CD相交于点D,连结AD,下列结论中不正确的是( )
Y
A.∠BAC=70°
B.∠DOC=90°
I
C.∠BDC=35°
D.∠DAC=55°4
8.如图所示,在△ABC中,∠C=90°,DE是AB的垂直平分线,∠BAD∶∠BAC=1∶3,则∠B=______.C
9.如图,在△ABC中,AD是它的角平分线,AB=6
cm,AC=8
cm,则S△ABD∶S△ACD=________,BD∶CD=________.f
10.如图,已知BD⊥AN于B,交AE于点O,OC⊥AM于点C,且OB=OC,如果∠OAB=25°,则∠ADB=________.e
11.如图,∠AOB内有点P,P1,P2分别是P关于OA,OB的对称点,P1P2交OA于M,交OB于N,若P1P2=5
cm,则△PMN的周长为________cm.o
12.如图,BD是∠ABC的角平分线,DE⊥AB于E,DF⊥BC于F,S△ABC=45
cm2,AB=12
cm,BC=18
cm,则DE的长是________.V
13.如图,已知:CD⊥AB于D,BE⊥AC于E,且BD=CE,BE交CD于点O.求证:AO平分∠BAC.E
14.如图所示,点P在线段AB的垂直平分线上,PC⊥PA,PD⊥PB,AC=BD,求证:点P在线段CD的垂直平分线上.
L
15.已知如图,AD是∠BAC的角平分线,DE⊥AB,DF⊥AC,垂足分别是E,F.k
求证:AD垂直平分EF.g
16.如图,在△ABC中,∠ACB=90°,CE⊥AB于点E,AD=AC,AF平分∠CAB交CE于点F,DF的延长线交AC于点G,试问:B4587478
(1)DF与BC有何位置关系?请说明理由;/
(2)FG与FE有何数量关系?请证明你的结论./
17.如图,△OBC中,BC的垂直平分线DP交∠BOC的平分线于D,垂足为P.V
(1)若∠BOC=60°,求∠BDC的度数;P
(2)若∠BOC=α,则∠BDC=________(直接写出结果).x4587478
答案:4587478
1---5
BCBBA
6.
B
7.
Bc
8.
22.5°Q
9.
3∶4
3∶4=
10.
40°=
11.
5
12.
3cm
13.
∵OD⊥AB,OE⊥AC,∴∠BDO=∠CEO=90°,又∵∠BOD=∠COE,BD=CE,∴△BOD≌△COE,∴OD=OE,又由已知条件得△AOD和△AOE都是直角三角形,且OD=OE,OA=OA,∴Rt△AOD≌Rt△AOE,∴∠DAO=∠EAO,即AO平分∠BAC
14.
∵点P在AB的垂直平分线上,∴PA=PB,∵PC⊥PA,PD⊥PB,∴∠BPD=∠APC=90°,又AC=BD,∴Rt△APC≌Rt△BPD(H.L.),∴PD=PC,∴点P在线段CD的垂直平分线上
15.
∵AD是∠BAC的角平分线,DE⊥AB,DF⊥AC,∴DE=DF,∴∠1=∠2,∵∠AED=∠AFD=90°,∴∠3=∠4,∴AE=AF,∵AD是等腰三角形AEF的顶角平分线,∴AD垂直平分EF(三线合一)
16.
(1)DF∥BC,理由是:∵AF平分∠BAC,∴∠CAF=∠DAF,在△CAF和△DAF中,,∴△CAF≌△DAF(S.A.S.),∴∠ADF=∠ACF,∵CE⊥AB,∠ACB=90°,∴∠CEB=∠ACB=90°,∴∠ACF+∠BCF=90°,∠B+∠BCF=90°,∴∠B=∠ACF=∠ADF,∴DF∥BC
(2)FG=EF,证明:∵DF∥BC,∠ACB=90°,∴∠AGF=∠ACB=90°,∴FG⊥AC,又∵CE⊥AB,AF平分∠CAB,∴FG=EF
17.
(1)过点D作DE⊥OB,交OB延长线于点E,DF⊥OC于F,∵OD是∠BOC的平分线,∴DE=DF,∵DP是BC的垂直平分线,∴BD=CD,在Rt△DEB和Rt△DFC中,,∴△DEB≌△DFC(H.L.),∴∠BDE=∠CDF,∴∠BDC=∠EDF,∵∠EOF+[JP]∠EDF=180°,∠BOC=60°,∴∠BDC=∠EDF=120°
(2)∵∠EOF+∠EDF=180°,∠BOC=α,∴∠BDC=∠EDF=180°-α.故答案为:180°-α
