九年级数学上册23.2.1中心对称课件
文档属性
| 名称 | 九年级数学上册23.2.1中心对称课件 |  | |
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-11-03 18:46:18 | ||
图片预览










文档简介
课件48张PPT。23.2.1 中心对称图形的旋转?如果图形上的点P经过旋转变为P’,那么这两点叫做这个旋转的对应点在平面内,将一个图形绕一个定点旋转一定的角度,这样的图形变换称为图形的旋转。这个定点称为旋转中心。转的角度称为旋转角。(4)对应点到旋转中心的距离相等.旋转的基本性质
(1)旋转不改变图形的大小和形状.(2)图形上的每一点都绕旋转中心沿相同方向转动了相同的角度(3)任意一对对应点与旋转中心的连线所成的角度都是旋转角.复习提问:1.什么是轴对称呢?2.关于轴对称的两个图形有哪些性质? 把一个图形沿着某一条直线折叠能与另一个图形完全重合,那么就说这两个图形关于这条直线对称或轴对称.1).两个图形是全等形.
2).对称轴是对称点连线的垂直平分线.3).图形的旋转:
在平面内,将一个图形绕一个定点旋转一定的角度,这样的图形变换称为图形的旋转,这个定点称为旋转中心,旋转的角度称为旋转角.
4).图形的旋转的性质:
①、旋转前后的图形全等.
②、对应点到旋转中心的距离相等.
③、对应点与旋转中心所连线段的夹角等于旋转角.
5).图形的旋转的作图:
先连结,再作角,最后截取.(1)把其中一个图案绕点O旋转180°.你有什么发现?
重 合重 合(2)线段AC,BD相交于点O,OA=OC,OB=OD.把 △OCD
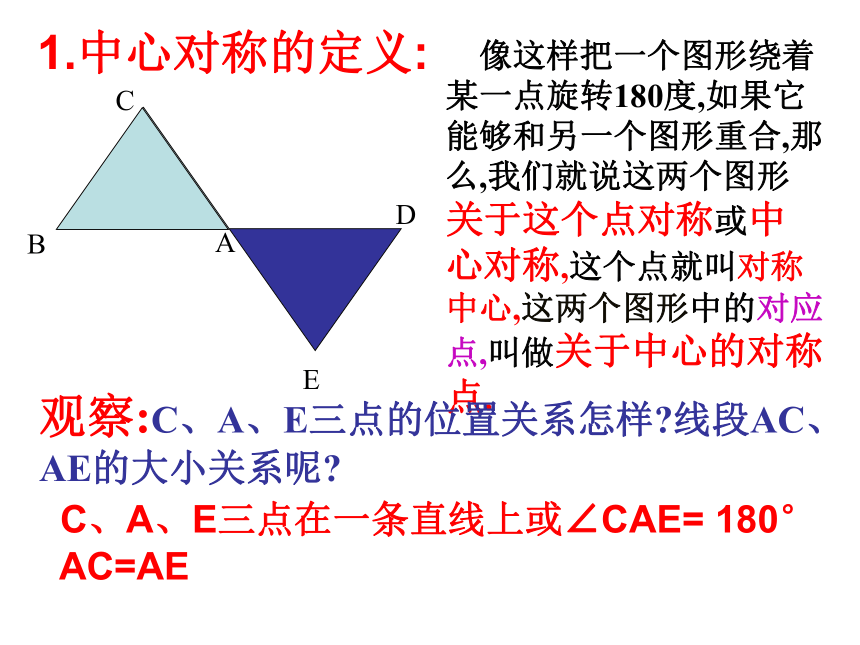
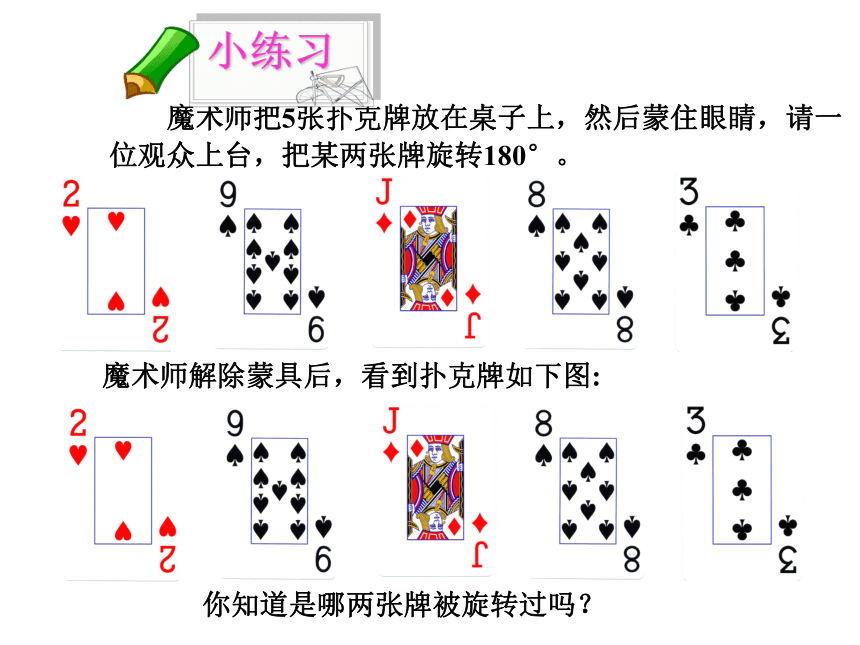
绕点O旋转180°.你有什么发现? OAODBC 像这样把一个图形绕着某一点旋转180度,如果它能够和另一个图形重合,那么,我们就说这两个图形关于这个点对称或中心对称,这个点就叫对称中心,这两个图形中的对应点,叫做关于中心的对称点.观察:C、A、E三点的位置关系怎样?线段AC、AE的大小关系呢?ACB C、A、E三点在一条直线上或∠CAE= 180° AC=AE1.中心对称的定义:下面的牌中哪些是中心对称图形?√√√ 魔术师把5张扑克牌放在桌子上,然后蒙住眼睛,请一位观众上台,把某两张牌旋转180°。 魔术师解除蒙具后,看到扑克牌如下图:你知道是哪两张牌被旋转过吗?汉代铜镜——中心对称图形 1. 选择题:
(1)下列图形中即是轴对称图形又是中心对称图形的是( )
A. 角 B. 等边三角形 C. 线段 D. 平行四边形C (2)下列多边形中,是中心对称图形而不是轴对称图形的是( )
A. 平行四边形 B. 矩形 C. 菱形 D. 正方形A 2. 判断下列说法是否正确。 (1)轴对称图形也是中心对称图形。( ) (2)旋转对称图形也是中心对称图形。( ) (3)平行四边形、长方形和正方形都是中心对称图形,对角线的交点是它们的对称中心。( ) (4)角是轴对称图形也是中心对称图形。( ) (5)在成中心对称的两个图形中,对应线段平行(或在同一直线上)且相等。 ( )×√×√ × 3. 判断下列图形是否是中心对称图形?√ ×√√√√√√ 4. 观察图形,并回答下面的问题:
(1)哪些只是轴对称图形?
(2)哪些只是中心对称图形?
(3)哪些既是轴对称图形,又是中心对称图形?(1)(3)(2)(4)(5)(6)(3)(4)(6)(1)(2)(5) 5. 在①线段、 ②角、 ③等腰三角形、 ④等腰梯形、⑤平行四边形、 ⑥矩形、 ⑦菱形、 ⑧正方形和⑨圆中,是轴对称图形的有______________
_______,是中心对称图形的有_______________,既是轴对称图形又是中心对称图形的有____________. ①⑤⑥⑦⑧⑨①②③④①⑥⑦⑧⑨⑥⑦⑧⑨ 6. 正三角形是中心对称图形吗?正方形呢?正五边形呢?正六边形呢?……你能发现什么规律?边数为偶数的正多边形都是中心对称图形。√ ×√ ×7. 下面的扑克牌中,哪些牌面是中心对称图形?√√√ 8. 在26个英文大写正体字母中,哪些字母是中心对称图形?A B C D E F G H I J K L M
N O P Q R S T U V W X Y Z旋转三角板,画关于点O对称的两个三角形:第一步,画出△ABC;第二步,以三角板的一个顶点O为中心,把三角板旋 转180°,画出△A′B′C′;O第三步,移开三角板.合作探究:合作探究:旋转三角板,画关于点O对称的两个三角形:分别连接AA’ ,BB’,CC’。
点O在线段AA′上吗?
如果在,在什么位置? △ABC与△A′B′C ′有什么关系?
(1)点O是线段AA ′的中点
(为什?) (2)△ABC≌△A′B′C′
(为什么?)第一步,画出△ABC;第二步,以三角板的一个顶点O为中心,把三角板旋 转180°,画出△A′B′C′;很显然画出的△ABC与△A’B’C’关于点O对称.第三步,移开三角板.(1). 点A′是绕点A旋转180°后得到的,即线段OA绕点O旋转180°得到线段OA′,所以点O在线段AA′上,且OA= OA′,即点O是线段AA′的中点.同样地,点O是线段BB′ CC′的中点. (2).在△AOB与△ A′ O B′中
OA=OA ′,OB=OB ′ ∠AOB= ∠AOB
∴ △AOB≌△ A′ O B′(SAS)
∴AB=A ′ B ′
同理 : BC=B ′ C ′,AC=A ′ C ′
∴ △ABC≌△ A′ B′C ′(SSS)证明:下图中△A′B′C′与△ABC关于点O是成中心对称的,你能从图中找到哪些等量关系?(1)OA=OA′、OB=OB′、 OC=OC′(2)△ABC≌△A′B′C′找一找:1)关于中心对称的两个图形,对称点所连 线段都经过对称中心,并且被对称中心所平 分.2)关于中心对称的两个图形是全等形。
2.归纳:中心对称的性质3)关于中心对称的两个图形,对称线段
平行且相等想一想 3.中心对称与轴对称有什么区别?又有什么联系?轴 对 称中心对称123翻转后和另一个图形重合旋转后和另一个图形重合2。判断正误:
(1)轴对称的两个图形一定是全等形,但全等的两个图形
不一定是轴对称的图形。( )
(2)成中心对称的两个图形一定是全等形。但全等的两个
图形不一定是成中心对称的图形。 ( )
(3)全等的两个图形,不是成中心对称的图形,就是成轴
对称的图形。 ( ) 3。选择题:
如果两个图形成中心对称,下列说法正确的是 ( )
(1)对称点连线必经过对称中心,且被对称中心平分。
(2)这两个图形一定是全等形。
(3)把一个图形绕着对称中心旋转后定与另一个图形重合。
(A)(1)(2)(3)(B)(2)(3)
(C)(1)(3) (D)(1)(2)D基础练习(一)4.中心对称的作图AOA'连结OA,并延长到A',使OA'=OA,例(1)已知A点和O点,画出
点A关于点O的对称点A'则A'是所求的点(2)已知线段AB和O点,画出线段AB关于点O的对称线段A' B' OA'B'AB连结AO并延长到A',使OA'=OA,
则得A的对称点A'
连结BO并延长到B' ,使O B' =OB,
则得B的对称点B'连结 A' B' ,则线段A' B'是所画线段(3).如图.选择点O为对称中心,画出与△ABC关于点O对称的△A′B′C′.解:A′C′B′△A′B′C′即为所求的三角形。
(4) 已知四边形ABCD和点O,画四边形A′B′C′D′,使它与已知四边形关于这一点对称。ABA′C′B′D′DOC四边形A1B1C1D1即为所求的图形。画一个与已知四边形ABCD中心对称图形。
(1)以顶点A为对称中心;
(2)以BC边的中点为对称中心。提高练习EFGMN 如图,已知△ABC与△A’B’C’中心对称,求出它们的对称中心O。应用解法一:根据观察,B、B’应是对应点,连结BB’,用刻度尺找出BB’的中点O,则点O即为所求(如图)OO解法二:根据观察,B、B’及C、C’应是两组对应点,连结BB’、CC’,BB’、CC’相交于点O,则点O即为所求(如图)。
练习:分别画出下列图形关于0对称的图形中心对称图形图1图2图3小组合作探究一4.中心对称图形的定义: 把一个图形绕着某一点旋转1800,如果旋转后的图形能够和原来的图形相互重合,那么这个图形叫中心对称图形。o练一练:下面哪个图形是中心对称图形?o判断下列图形是不是中心对称图形 : 练一练 中心对称与中心对称图形是两个既有联系又有 区别的概念 区别: 中心对称指两个全等图形的相互位置关系
中心对称图形指一个图形本身成中心对称联系: (1)如果将中心对称图形的两个图形看成一个整体,则它们是中心对称图形 (2)如果将中心对称图形,把对称的部分看
成两个图形,则它们是关于中心对称。 两个人轮流在桌子上摆放硬币.规则是每人每次摆一个在桌面上,摆好之后不许移动.不允许任何两枚硬币有重叠部分,这样经过多次摆放,规定谁放下最后一枚,并使得对方没有再放的位置,就算是谁获胜。
按照这个规则你用什么方法才能取胜呢?需要智慧的游戏分析:设想桌面很小,仅与硬币同样大小,这时显然是先放者一定获胜。再设想桌面直径仅为硬币直径的2倍,这时,先放者为了获胜,肯定不会将硬币放的挨上圆桌边缘,只要他让硬币压上桌面中心,就使对方无法再放了。看来,桌面中心是个举足轻重的位置,值得认真对待,对于一般圆桌,设想甲先置一枚硬币于圆桌中心,待乙方置一枚硬币于桌面上A处后,甲再往A处,A处关于中心的对称位置放置一枚,这样轮流下去,只要乙有位置放,甲就也有。
解:先放者获胜,操作办法是,第一枚硬币要放在桌面中心处,然后每次都往对方所放位置关于
桌面中心的对称处放。 你要争取先放,并把第1枚硬币放在桌面的对称中心上,以后你应该根据对方所放硬币的位置,在它关于中心对称的位置上放下一枚同样大小硬币.这样,由于对称性,只要对方能放得下一枚硬币,你就保证能在其对称位置上放下一枚同样大小的硬币,因此,失败绝对轮不到你. 分析:谢谢!下课了!再见
(1)旋转不改变图形的大小和形状.(2)图形上的每一点都绕旋转中心沿相同方向转动了相同的角度(3)任意一对对应点与旋转中心的连线所成的角度都是旋转角.复习提问:1.什么是轴对称呢?2.关于轴对称的两个图形有哪些性质? 把一个图形沿着某一条直线折叠能与另一个图形完全重合,那么就说这两个图形关于这条直线对称或轴对称.1).两个图形是全等形.
2).对称轴是对称点连线的垂直平分线.3).图形的旋转:
在平面内,将一个图形绕一个定点旋转一定的角度,这样的图形变换称为图形的旋转,这个定点称为旋转中心,旋转的角度称为旋转角.
4).图形的旋转的性质:
①、旋转前后的图形全等.
②、对应点到旋转中心的距离相等.
③、对应点与旋转中心所连线段的夹角等于旋转角.
5).图形的旋转的作图:
先连结,再作角,最后截取.(1)把其中一个图案绕点O旋转180°.你有什么发现?
重 合重 合(2)线段AC,BD相交于点O,OA=OC,OB=OD.把 △OCD
绕点O旋转180°.你有什么发现? OAODBC 像这样把一个图形绕着某一点旋转180度,如果它能够和另一个图形重合,那么,我们就说这两个图形关于这个点对称或中心对称,这个点就叫对称中心,这两个图形中的对应点,叫做关于中心的对称点.观察:C、A、E三点的位置关系怎样?线段AC、AE的大小关系呢?ACB C、A、E三点在一条直线上或∠CAE= 180° AC=AE1.中心对称的定义:下面的牌中哪些是中心对称图形?√√√ 魔术师把5张扑克牌放在桌子上,然后蒙住眼睛,请一位观众上台,把某两张牌旋转180°。 魔术师解除蒙具后,看到扑克牌如下图:你知道是哪两张牌被旋转过吗?汉代铜镜——中心对称图形 1. 选择题:
(1)下列图形中即是轴对称图形又是中心对称图形的是( )
A. 角 B. 等边三角形 C. 线段 D. 平行四边形C (2)下列多边形中,是中心对称图形而不是轴对称图形的是( )
A. 平行四边形 B. 矩形 C. 菱形 D. 正方形A 2. 判断下列说法是否正确。 (1)轴对称图形也是中心对称图形。( ) (2)旋转对称图形也是中心对称图形。( ) (3)平行四边形、长方形和正方形都是中心对称图形,对角线的交点是它们的对称中心。( ) (4)角是轴对称图形也是中心对称图形。( ) (5)在成中心对称的两个图形中,对应线段平行(或在同一直线上)且相等。 ( )×√×√ × 3. 判断下列图形是否是中心对称图形?√ ×√√√√√√ 4. 观察图形,并回答下面的问题:
(1)哪些只是轴对称图形?
(2)哪些只是中心对称图形?
(3)哪些既是轴对称图形,又是中心对称图形?(1)(3)(2)(4)(5)(6)(3)(4)(6)(1)(2)(5) 5. 在①线段、 ②角、 ③等腰三角形、 ④等腰梯形、⑤平行四边形、 ⑥矩形、 ⑦菱形、 ⑧正方形和⑨圆中,是轴对称图形的有______________
_______,是中心对称图形的有_______________,既是轴对称图形又是中心对称图形的有____________. ①⑤⑥⑦⑧⑨①②③④①⑥⑦⑧⑨⑥⑦⑧⑨ 6. 正三角形是中心对称图形吗?正方形呢?正五边形呢?正六边形呢?……你能发现什么规律?边数为偶数的正多边形都是中心对称图形。√ ×√ ×7. 下面的扑克牌中,哪些牌面是中心对称图形?√√√ 8. 在26个英文大写正体字母中,哪些字母是中心对称图形?A B C D E F G H I J K L M
N O P Q R S T U V W X Y Z旋转三角板,画关于点O对称的两个三角形:第一步,画出△ABC;第二步,以三角板的一个顶点O为中心,把三角板旋 转180°,画出△A′B′C′;O第三步,移开三角板.合作探究:合作探究:旋转三角板,画关于点O对称的两个三角形:分别连接AA’ ,BB’,CC’。
点O在线段AA′上吗?
如果在,在什么位置? △ABC与△A′B′C ′有什么关系?
(1)点O是线段AA ′的中点
(为什?) (2)△ABC≌△A′B′C′
(为什么?)第一步,画出△ABC;第二步,以三角板的一个顶点O为中心,把三角板旋 转180°,画出△A′B′C′;很显然画出的△ABC与△A’B’C’关于点O对称.第三步,移开三角板.(1). 点A′是绕点A旋转180°后得到的,即线段OA绕点O旋转180°得到线段OA′,所以点O在线段AA′上,且OA= OA′,即点O是线段AA′的中点.同样地,点O是线段BB′ CC′的中点. (2).在△AOB与△ A′ O B′中
OA=OA ′,OB=OB ′ ∠AOB= ∠AOB
∴ △AOB≌△ A′ O B′(SAS)
∴AB=A ′ B ′
同理 : BC=B ′ C ′,AC=A ′ C ′
∴ △ABC≌△ A′ B′C ′(SSS)证明:下图中△A′B′C′与△ABC关于点O是成中心对称的,你能从图中找到哪些等量关系?(1)OA=OA′、OB=OB′、 OC=OC′(2)△ABC≌△A′B′C′找一找:1)关于中心对称的两个图形,对称点所连 线段都经过对称中心,并且被对称中心所平 分.2)关于中心对称的两个图形是全等形。
2.归纳:中心对称的性质3)关于中心对称的两个图形,对称线段
平行且相等想一想 3.中心对称与轴对称有什么区别?又有什么联系?轴 对 称中心对称123翻转后和另一个图形重合旋转后和另一个图形重合2。判断正误:
(1)轴对称的两个图形一定是全等形,但全等的两个图形
不一定是轴对称的图形。( )
(2)成中心对称的两个图形一定是全等形。但全等的两个
图形不一定是成中心对称的图形。 ( )
(3)全等的两个图形,不是成中心对称的图形,就是成轴
对称的图形。 ( ) 3。选择题:
如果两个图形成中心对称,下列说法正确的是 ( )
(1)对称点连线必经过对称中心,且被对称中心平分。
(2)这两个图形一定是全等形。
(3)把一个图形绕着对称中心旋转后定与另一个图形重合。
(A)(1)(2)(3)(B)(2)(3)
(C)(1)(3) (D)(1)(2)D基础练习(一)4.中心对称的作图AOA'连结OA,并延长到A',使OA'=OA,例(1)已知A点和O点,画出
点A关于点O的对称点A'则A'是所求的点(2)已知线段AB和O点,画出线段AB关于点O的对称线段A' B' OA'B'AB连结AO并延长到A',使OA'=OA,
则得A的对称点A'
连结BO并延长到B' ,使O B' =OB,
则得B的对称点B'连结 A' B' ,则线段A' B'是所画线段(3).如图.选择点O为对称中心,画出与△ABC关于点O对称的△A′B′C′.解:A′C′B′△A′B′C′即为所求的三角形。
(4) 已知四边形ABCD和点O,画四边形A′B′C′D′,使它与已知四边形关于这一点对称。ABA′C′B′D′DOC四边形A1B1C1D1即为所求的图形。画一个与已知四边形ABCD中心对称图形。
(1)以顶点A为对称中心;
(2)以BC边的中点为对称中心。提高练习EFGMN 如图,已知△ABC与△A’B’C’中心对称,求出它们的对称中心O。应用解法一:根据观察,B、B’应是对应点,连结BB’,用刻度尺找出BB’的中点O,则点O即为所求(如图)OO解法二:根据观察,B、B’及C、C’应是两组对应点,连结BB’、CC’,BB’、CC’相交于点O,则点O即为所求(如图)。
练习:分别画出下列图形关于0对称的图形中心对称图形图1图2图3小组合作探究一4.中心对称图形的定义: 把一个图形绕着某一点旋转1800,如果旋转后的图形能够和原来的图形相互重合,那么这个图形叫中心对称图形。o练一练:下面哪个图形是中心对称图形?o判断下列图形是不是中心对称图形 : 练一练 中心对称与中心对称图形是两个既有联系又有 区别的概念 区别: 中心对称指两个全等图形的相互位置关系
中心对称图形指一个图形本身成中心对称联系: (1)如果将中心对称图形的两个图形看成一个整体,则它们是中心对称图形 (2)如果将中心对称图形,把对称的部分看
成两个图形,则它们是关于中心对称。 两个人轮流在桌子上摆放硬币.规则是每人每次摆一个在桌面上,摆好之后不许移动.不允许任何两枚硬币有重叠部分,这样经过多次摆放,规定谁放下最后一枚,并使得对方没有再放的位置,就算是谁获胜。
按照这个规则你用什么方法才能取胜呢?需要智慧的游戏分析:设想桌面很小,仅与硬币同样大小,这时显然是先放者一定获胜。再设想桌面直径仅为硬币直径的2倍,这时,先放者为了获胜,肯定不会将硬币放的挨上圆桌边缘,只要他让硬币压上桌面中心,就使对方无法再放了。看来,桌面中心是个举足轻重的位置,值得认真对待,对于一般圆桌,设想甲先置一枚硬币于圆桌中心,待乙方置一枚硬币于桌面上A处后,甲再往A处,A处关于中心的对称位置放置一枚,这样轮流下去,只要乙有位置放,甲就也有。
解:先放者获胜,操作办法是,第一枚硬币要放在桌面中心处,然后每次都往对方所放位置关于
桌面中心的对称处放。 你要争取先放,并把第1枚硬币放在桌面的对称中心上,以后你应该根据对方所放硬币的位置,在它关于中心对称的位置上放下一枚同样大小硬币.这样,由于对称性,只要对方能放得下一枚硬币,你就保证能在其对称位置上放下一枚同样大小的硬币,因此,失败绝对轮不到你. 分析:谢谢!下课了!再见
同课章节目录
