九年级上24.4弧长和扇形面积公开课课件
文档属性
| 名称 | 九年级上24.4弧长和扇形面积公开课课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-11-03 18:52:17 | ||
图片预览





文档简介
课件22张PPT。弧长和扇形的面积 教学目标
1.探索弧长计算公式和扇形计算公式并能够从公式来源的角度上加以理解
2.熟练应用公式并能解决相关的实际问题
3.理解并把握课程中涵盖的数学思想和数学方法并加以应用
重点:两个公式
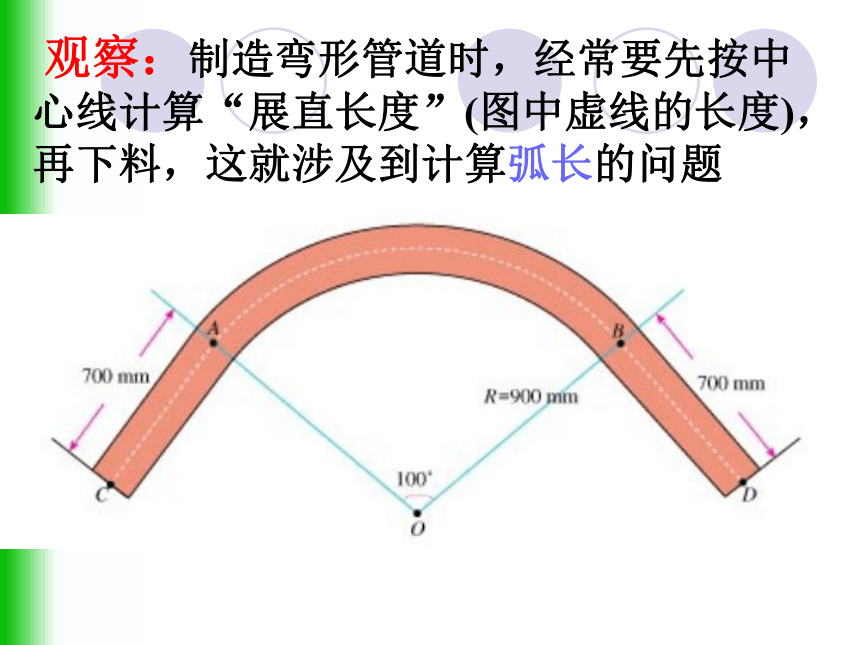
难点:实际问题的解决及思想方法的运用 观察:制造弯形管道时,经常要先按中心线计算“展直长度”(图中虚线的长度),再下料,这就涉及到计算弧长的问题
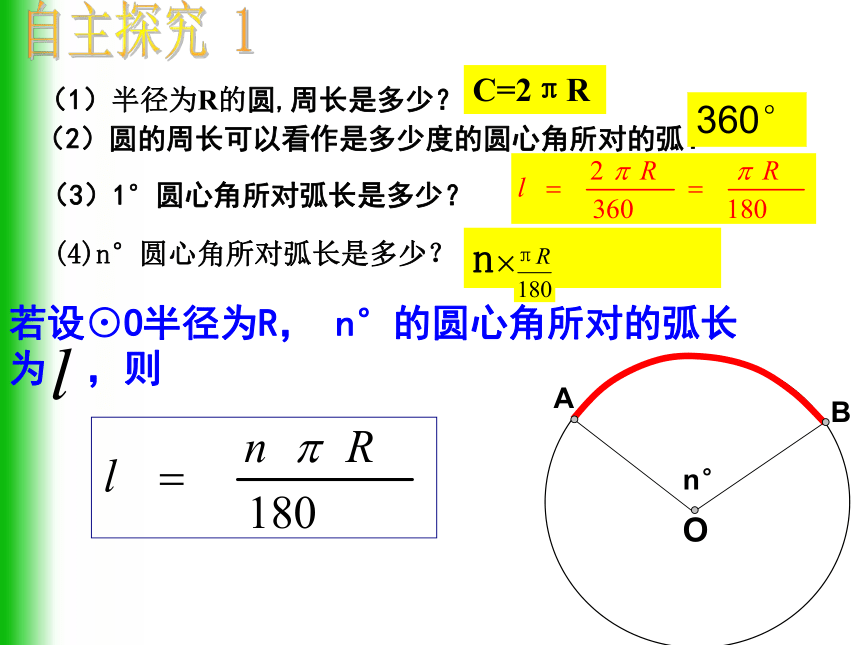
(1)半径为R的圆,周长是多少?C=2πR (3)1°圆心角所对弧长是多少? (2)圆的周长可以看作是多少度的圆心角所对的弧?n°ABO自主探究 1360°(4)n°圆心角所对弧长是多少?试一试1.已知弧所对的圆心角为900,半径是4,则弧长为______
2. 已知一条弧的半径为9,弧长为8 π ,那么这条弧所对的圆心角为____。
3. 钟表的轴心到分针针端的长为5cm,那么经过40分钟,分针针端转过的弧长是( )
A. B. C. D. 160°B小结: 弧长公式涉及三个量 :1,弧长 ,2,圆心角的度数 ,3,弧所在的半径,知道其中两个量,就可以求第三个量。
应用:制造弯形管道时,要先按中心线计算“展直长度”,再下料,试计算图所示管道的展直长度L(单位:mm,精确到1mm)
解:由弧长公式,可得弧AB 的长
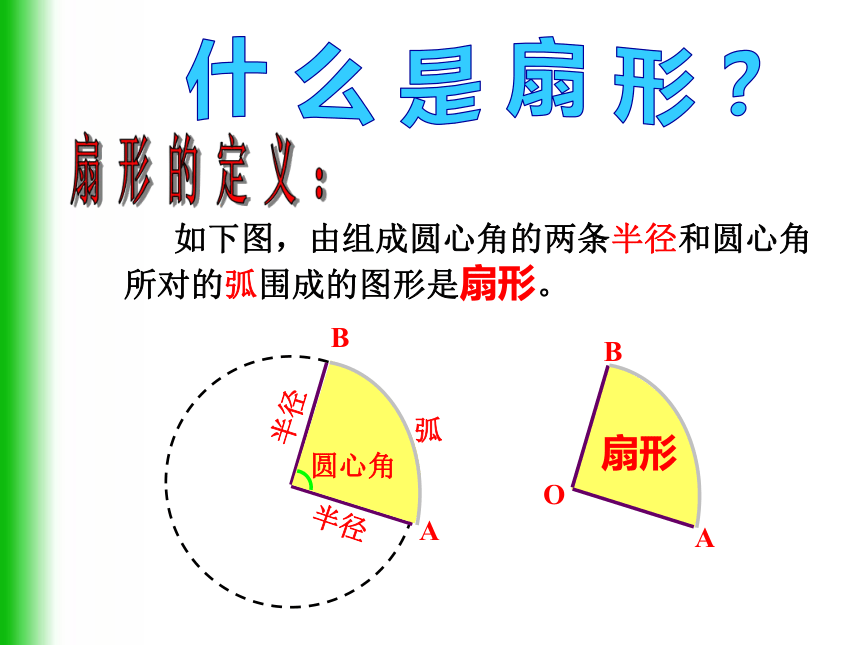
因此所要求的展直长度 答:管道的展直长度为2970mm. 什 么 是 扇 形 ?扇 形 的 定 义 : 如下图,由组成圆心角的两条半径和圆心角所对的弧围成的图形是扇形。圆心角圆心角AB那么: 在半径为R 的圆中,n°的圆心角所对的扇形面积的计算公式为自主探究 2360°(1) 如果圆的半径为R,则圆的面积为多少?
(2)圆的面积可以看成多少度圆心角扇形的面积?(3) l°的圆心角对应的扇形面积为多少 ?(4) n°的圆心角对应的扇形面积为 多少?比较扇形面积与弧长公式, 用弧长表示扇形面积:想一想:扇形的面积公式与什么
公式类似?知识之间3、已知扇形的圆心角为1500,弧长为 ,则扇形的面积为__________.2、已知扇形的圆心角为300,面积为 ,则这个扇形的半径R=____. 1、已知扇形的圆心角为120°,半径为2,则这个扇形的面积为_______.6cm做一做:小结: 扇形面积公式涉及三个量 扇形面积 ,圆心角的度数 ,弧所在的半径,知道其中两个量,就可以求第三个量。
例1.如图、水平放置的圆柱形排水管道的截面半径是0.6cm,其中水面高0.3cm,求截面上有水部分的面积。CDS弓形= S扇形- S△拓展应用练习:如图、水平放置的圆柱形排水管道的截面半径是0.6cm,其中水面高0.9cm,求截面上有水部分的面积。ABDCE变式训练S弓形= S扇形+S△感悟:
①当弓形面积小于半圆时
S弓形= S扇形-S△
②当弓形面积大于半圆时
S弓形= S扇形+S△效果检测 已知等边三角形ABC的边长为a,分别以A、B、C为圆心,以 为半径的圆相切于点D、 E、F,求图中阴影部分的面积S.(2009年长春)如图,方格纸中4个
小正方形的边长均为1,则图中阴影部分三个
小扇形的面积和为 (结果保留).
点击中考回顾与归纳(一)1.弧长公式:2.扇形面积公式:注意:两个公式的联系和区别3.学会几何建模,既把实际问题转化为几何问题(把实际问题中的条件和结论与数学问题中的条件和结论对应起来是解题之关键)
回顾与归纳(二)组合图形的面积:(1)割补法(2)组合法其中:
①当弓形面积小于半圆时S弓形= S扇形-S△
②当弓形面积大于半圆时S弓形= S扇形+S△
数学思想(1)转化思想、(2)整体思想一句话小结:四个公式、一个问题、两种思想、两个方法.当堂检测1. 某中学的铅球场如图所示,已知扇形AOB的面积是36,弧AB的长度为9,求半径OA是多少? 2. (2006,武汉)如图,⊙A、⊙B、⊙C、⊙D相互外离,它们的半径都是1,顺次连接四个圆心得到四边形ABCD,则图形中四个扇形(空白部分)的面积之和是多少?3 如图所示,PA,PB切⊙于A,B两点,若∠APB=60°,⊙的半径为3,求阴影部分的面积。 练习册P57
选做P57创新探究题作业努力,成功一定是属于你!!!再见
1.探索弧长计算公式和扇形计算公式并能够从公式来源的角度上加以理解
2.熟练应用公式并能解决相关的实际问题
3.理解并把握课程中涵盖的数学思想和数学方法并加以应用
重点:两个公式
难点:实际问题的解决及思想方法的运用 观察:制造弯形管道时,经常要先按中心线计算“展直长度”(图中虚线的长度),再下料,这就涉及到计算弧长的问题
(1)半径为R的圆,周长是多少?C=2πR (3)1°圆心角所对弧长是多少? (2)圆的周长可以看作是多少度的圆心角所对的弧?n°ABO自主探究 1360°(4)n°圆心角所对弧长是多少?试一试1.已知弧所对的圆心角为900,半径是4,则弧长为______
2. 已知一条弧的半径为9,弧长为8 π ,那么这条弧所对的圆心角为____。
3. 钟表的轴心到分针针端的长为5cm,那么经过40分钟,分针针端转过的弧长是( )
A. B. C. D. 160°B小结: 弧长公式涉及三个量 :1,弧长 ,2,圆心角的度数 ,3,弧所在的半径,知道其中两个量,就可以求第三个量。
应用:制造弯形管道时,要先按中心线计算“展直长度”,再下料,试计算图所示管道的展直长度L(单位:mm,精确到1mm)
解:由弧长公式,可得弧AB 的长
因此所要求的展直长度 答:管道的展直长度为2970mm. 什 么 是 扇 形 ?扇 形 的 定 义 : 如下图,由组成圆心角的两条半径和圆心角所对的弧围成的图形是扇形。圆心角圆心角AB那么: 在半径为R 的圆中,n°的圆心角所对的扇形面积的计算公式为自主探究 2360°(1) 如果圆的半径为R,则圆的面积为多少?
(2)圆的面积可以看成多少度圆心角扇形的面积?(3) l°的圆心角对应的扇形面积为多少 ?(4) n°的圆心角对应的扇形面积为 多少?比较扇形面积与弧长公式, 用弧长表示扇形面积:想一想:扇形的面积公式与什么
公式类似?知识之间3、已知扇形的圆心角为1500,弧长为 ,则扇形的面积为__________.2、已知扇形的圆心角为300,面积为 ,则这个扇形的半径R=____. 1、已知扇形的圆心角为120°,半径为2,则这个扇形的面积为_______.6cm做一做:小结: 扇形面积公式涉及三个量 扇形面积 ,圆心角的度数 ,弧所在的半径,知道其中两个量,就可以求第三个量。
例1.如图、水平放置的圆柱形排水管道的截面半径是0.6cm,其中水面高0.3cm,求截面上有水部分的面积。CDS弓形= S扇形- S△拓展应用练习:如图、水平放置的圆柱形排水管道的截面半径是0.6cm,其中水面高0.9cm,求截面上有水部分的面积。ABDCE变式训练S弓形= S扇形+S△感悟:
①当弓形面积小于半圆时
S弓形= S扇形-S△
②当弓形面积大于半圆时
S弓形= S扇形+S△效果检测 已知等边三角形ABC的边长为a,分别以A、B、C为圆心,以 为半径的圆相切于点D、 E、F,求图中阴影部分的面积S.(2009年长春)如图,方格纸中4个
小正方形的边长均为1,则图中阴影部分三个
小扇形的面积和为 (结果保留).
点击中考回顾与归纳(一)1.弧长公式:2.扇形面积公式:注意:两个公式的联系和区别3.学会几何建模,既把实际问题转化为几何问题(把实际问题中的条件和结论与数学问题中的条件和结论对应起来是解题之关键)
回顾与归纳(二)组合图形的面积:(1)割补法(2)组合法其中:
①当弓形面积小于半圆时S弓形= S扇形-S△
②当弓形面积大于半圆时S弓形= S扇形+S△
数学思想(1)转化思想、(2)整体思想一句话小结:四个公式、一个问题、两种思想、两个方法.当堂检测1. 某中学的铅球场如图所示,已知扇形AOB的面积是36,弧AB的长度为9,求半径OA是多少? 2. (2006,武汉)如图,⊙A、⊙B、⊙C、⊙D相互外离,它们的半径都是1,顺次连接四个圆心得到四边形ABCD,则图形中四个扇形(空白部分)的面积之和是多少?3 如图所示,PA,PB切⊙于A,B两点,若∠APB=60°,⊙的半径为3,求阴影部分的面积。 练习册P57
选做P57创新探究题作业努力,成功一定是属于你!!!再见
同课章节目录
