1.2.1函数的概念(带解析)
文档属性
| 名称 | 1.2.1函数的概念(带解析) |  | |
| 格式 | zip | ||
| 文件大小 | 514.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-11-07 15:04:10 | ||
图片预览


文档简介
1.2.1函数的概念(带解析)
一、选择题
1.区间(-3,2]用集合表示为( )
A.{-2,-1,0,1,2} B.{x|-3<x<2}
C.{x|-3<x≤2} D.{x|-3≤x≤2}
2.下列四组中的f(x),g(x)表示同一个函数的是( )
A. B. C. D.f(x)=1,g(x)=x
3.函数f(x)=+的定义域为( )
A.(﹣3,0] B.(﹣3,1]
C.(﹣∞,﹣3)∪(﹣3,0] D.(﹣∞,﹣3)∪(﹣3,1]
4.下列各组函数中表示同一函数的是( )
①f(x)=与g(x)=;
②f(x)=|x|与g(x)=;
③f(x)=x0与g(x)=;
④f(x)=x2-2x-1与g(t)=t2-2t-1.
A.①② B.②③ C.③④ D.①④
5.( )
A.(﹣∞,2] B.(0,+∞)
C.[2,+∞) D.[0,2]
6.已知g(x)=1-2x,f[g(x)]=(x≠0),则f()等于( )
A.15 B.1 C.3 D.30
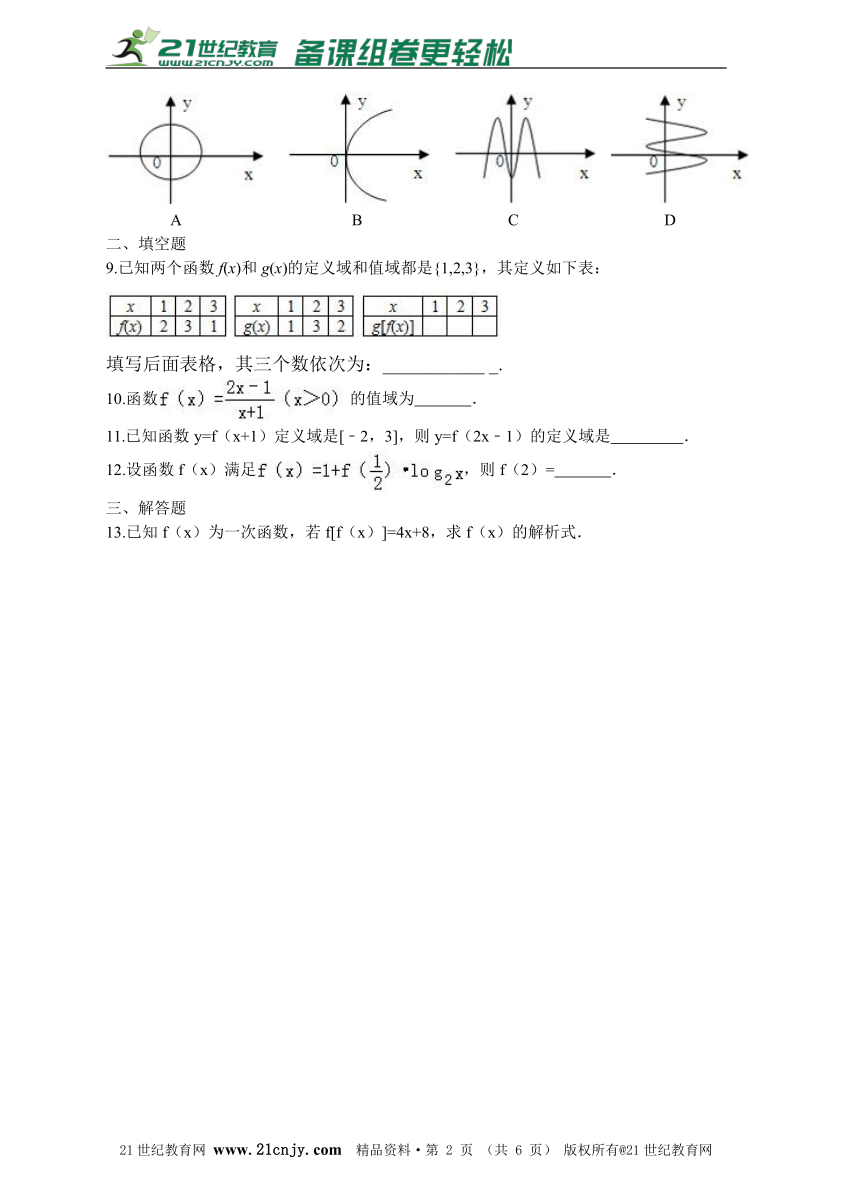
7.下列四个图形中,不是以x为自变量的函数的图象是( )
A B C D21教育网
8.下列图象中表示函数图象的是( )
A B C D
二、填空题
9.已知两个函数f(x)和g(x)的定义域和值域都是{1,2,3},其定义如下表:
填写后面表格,其三个数依次为:___________ _.
10.函数的值域为 .
11.已知函数y=f(x+1)定义域是[﹣2,3],则y=f(2x﹣1)的定义域是 .
12.设函数f(x)满足,则f(2)= .
三、解答题
13.已知f(x)为一次函数,若f[f(x)]=4x+8,求f(x)的解析式.
14.已知函数.
(1)当时,求函数在上的值域;
(2)是否存在实数,是函数的定义域为,值域为?若存在,求出的值;若不存在,请说明理由.
参考答案及解析
1.C 【解析】由区间和集合的关系可得,区间(-3,2]可表示为:{x|-3<x≤2} 2.A 【解析】f(x)=x3?与 g(x)=具有相同的定义域、值域、对应关系,故表示同一个函数,
不相同,③的定义域相同,都是,都能化简为,所以③是同一函数,④的定义域相同,解析式也相同,所以是同一函数,故选C.21世纪教育网版权所有
5.D
【解析】根据函数≥0,而且﹣x2﹣2x+3=﹣(x+1)2+4≤4,从而求得函数的值域.
∵函数≥0,
而且﹣x2﹣2x+3=﹣( x2+2x﹣3)=﹣(x+1)2+4≤4,∴≤2,
∴0≤f(x)≤2,
6.分析:可令g(x)=,得出x的值,再代入可得答案. 【解析】令g(x)=,得1-2x=,解得x=. ∴f()=f[g()]===15. 7.C 【解析】由函数定义知,定义域内的每一个x都有唯一函数值与之对应, A、B、D选项中的图象都符合;C项中对于大于零的x而言,有两个不同的值与之对应,不符合函数定义. 8.C 【解析】根据函数的定义,对任意的一个x都存在唯一的y与之对应 而A、B、D都是一对多,只有C是多对一. 9.3 2 121cnjy.com
【解析】g[f(1)]=g(2)=3,g[f(2)]=g(3)=2,
g[f(3)]=g(1)=1. 10.(﹣1,2)
【解析】分析出x>0时,函数为增函数,结合反比例型函数的图象和性质,可得答案.
∵
【解析】通过表达式求出f(),然后求出函数的解析式,即可求解f(2)的值.
因为,
所以.
,
∴.
∴=.
13.或f(x)=-2x-8 【解析】设一次函数f(x)=ax+b(a≠0), 则f[f(x)]=af(x)+b=a(ax+b)+b=a2x+ab+b, 又f[f(x)]=4x+8, 则有a2x+ab+b=4x+8,得或, 故所求函数的解析式为:或f(x)=-2x-8. 当时,由,不存在;21·cn·jy·com
当时,由,所以(舍去)
综上所述.
一、选择题
1.区间(-3,2]用集合表示为( )
A.{-2,-1,0,1,2} B.{x|-3<x<2}
C.{x|-3<x≤2} D.{x|-3≤x≤2}
2.下列四组中的f(x),g(x)表示同一个函数的是( )
A. B. C. D.f(x)=1,g(x)=x
3.函数f(x)=+的定义域为( )
A.(﹣3,0] B.(﹣3,1]
C.(﹣∞,﹣3)∪(﹣3,0] D.(﹣∞,﹣3)∪(﹣3,1]
4.下列各组函数中表示同一函数的是( )
①f(x)=与g(x)=;
②f(x)=|x|与g(x)=;
③f(x)=x0与g(x)=;
④f(x)=x2-2x-1与g(t)=t2-2t-1.
A.①② B.②③ C.③④ D.①④
5.( )
A.(﹣∞,2] B.(0,+∞)
C.[2,+∞) D.[0,2]
6.已知g(x)=1-2x,f[g(x)]=(x≠0),则f()等于( )
A.15 B.1 C.3 D.30
7.下列四个图形中,不是以x为自变量的函数的图象是( )
A B C D21教育网
8.下列图象中表示函数图象的是( )
A B C D
二、填空题
9.已知两个函数f(x)和g(x)的定义域和值域都是{1,2,3},其定义如下表:
填写后面表格,其三个数依次为:___________ _.
10.函数的值域为 .
11.已知函数y=f(x+1)定义域是[﹣2,3],则y=f(2x﹣1)的定义域是 .
12.设函数f(x)满足,则f(2)= .
三、解答题
13.已知f(x)为一次函数,若f[f(x)]=4x+8,求f(x)的解析式.
14.已知函数.
(1)当时,求函数在上的值域;
(2)是否存在实数,是函数的定义域为,值域为?若存在,求出的值;若不存在,请说明理由.
参考答案及解析
1.C 【解析】由区间和集合的关系可得,区间(-3,2]可表示为:{x|-3<x≤2} 2.A 【解析】f(x)=x3?与 g(x)=具有相同的定义域、值域、对应关系,故表示同一个函数,
不相同,③的定义域相同,都是,都能化简为,所以③是同一函数,④的定义域相同,解析式也相同,所以是同一函数,故选C.21世纪教育网版权所有
5.D
【解析】根据函数≥0,而且﹣x2﹣2x+3=﹣(x+1)2+4≤4,从而求得函数的值域.
∵函数≥0,
而且﹣x2﹣2x+3=﹣( x2+2x﹣3)=﹣(x+1)2+4≤4,∴≤2,
∴0≤f(x)≤2,
6.分析:可令g(x)=,得出x的值,再代入可得答案. 【解析】令g(x)=,得1-2x=,解得x=. ∴f()=f[g()]===15. 7.C 【解析】由函数定义知,定义域内的每一个x都有唯一函数值与之对应, A、B、D选项中的图象都符合;C项中对于大于零的x而言,有两个不同的值与之对应,不符合函数定义. 8.C 【解析】根据函数的定义,对任意的一个x都存在唯一的y与之对应 而A、B、D都是一对多,只有C是多对一. 9.3 2 121cnjy.com
【解析】g[f(1)]=g(2)=3,g[f(2)]=g(3)=2,
g[f(3)]=g(1)=1. 10.(﹣1,2)
【解析】分析出x>0时,函数为增函数,结合反比例型函数的图象和性质,可得答案.
∵
【解析】通过表达式求出f(),然后求出函数的解析式,即可求解f(2)的值.
因为,
所以.
,
∴.
∴=.
13.或f(x)=-2x-8 【解析】设一次函数f(x)=ax+b(a≠0), 则f[f(x)]=af(x)+b=a(ax+b)+b=a2x+ab+b, 又f[f(x)]=4x+8, 则有a2x+ab+b=4x+8,得或, 故所求函数的解析式为:或f(x)=-2x-8. 当时,由,不存在;21·cn·jy·com
当时,由,所以(舍去)
综上所述.
