九年级数学上册24.1.2垂直于弦的直径课件
文档属性
| 名称 | 九年级数学上册24.1.2垂直于弦的直径课件 |  | |
| 格式 | zip | ||
| 文件大小 | 213.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-11-03 19:15:16 | ||
图片预览




文档简介
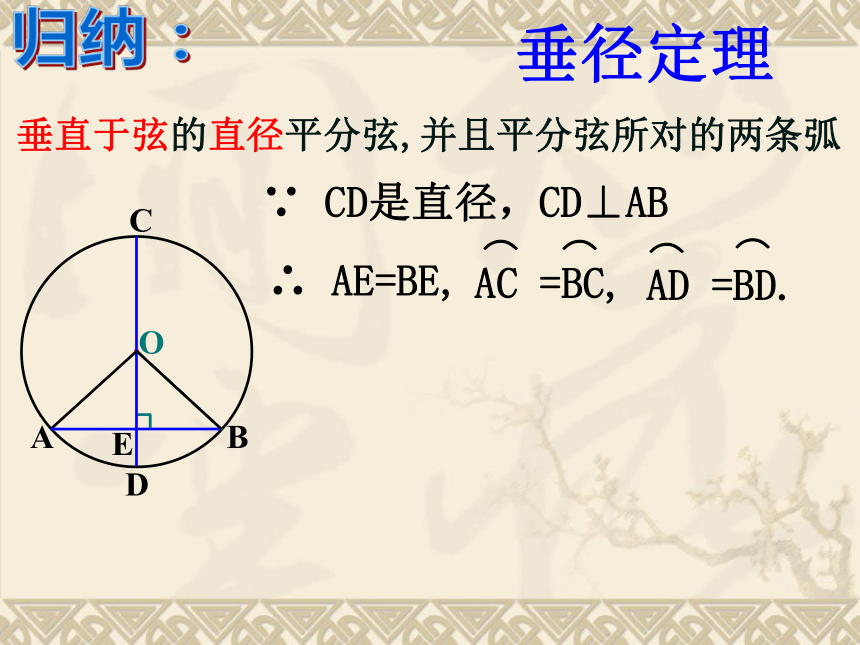
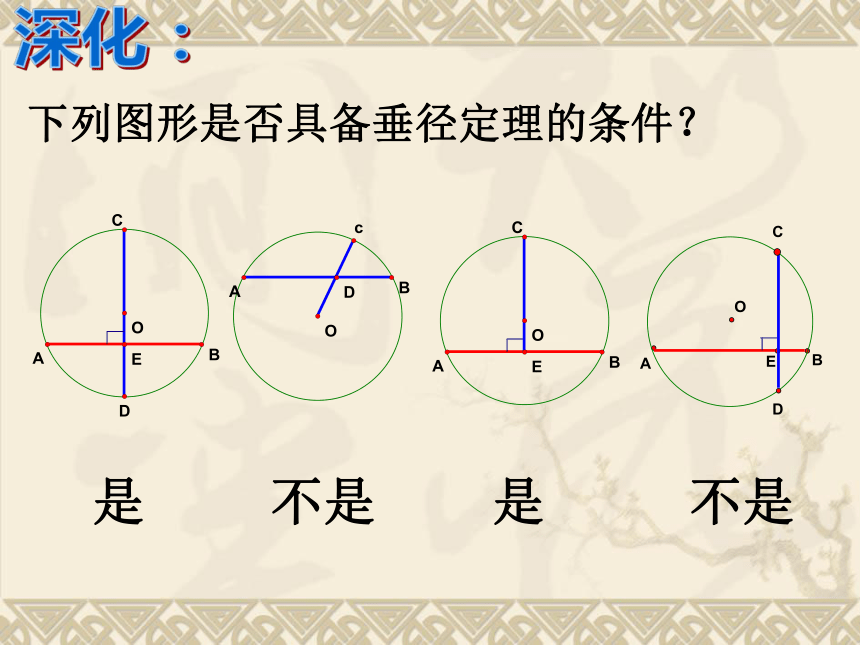
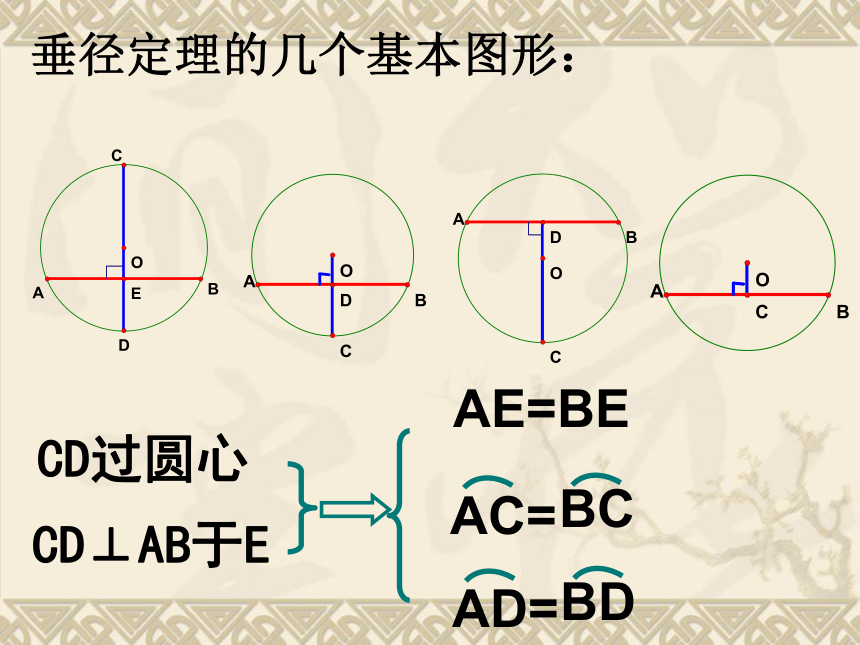
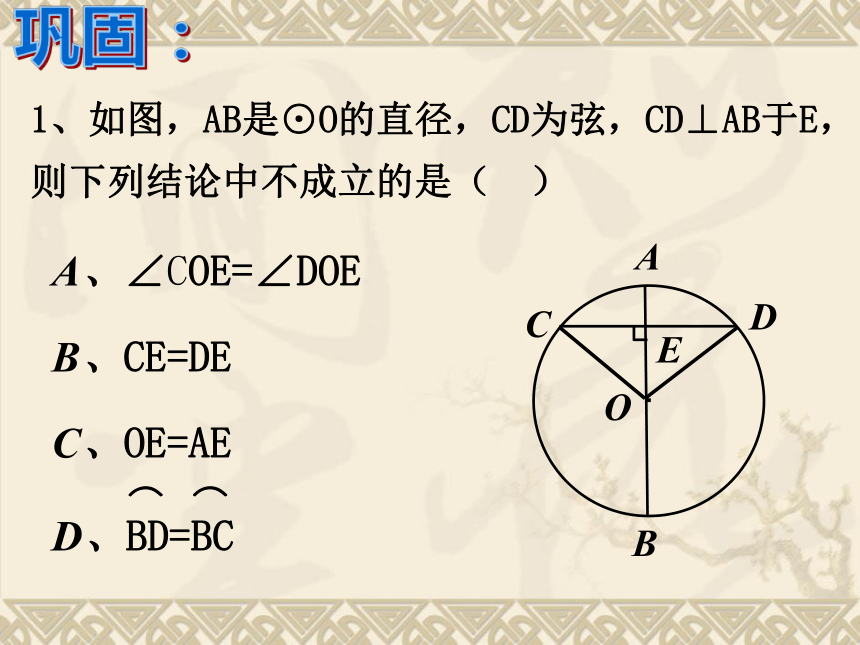
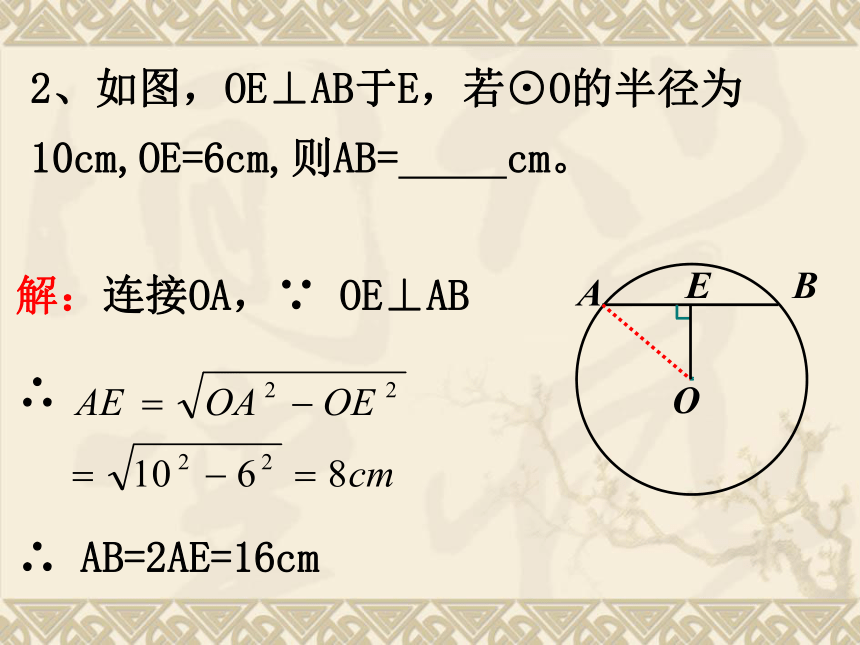
课件25张PPT。24.1.2 垂直于弦的直径问题 :你知道赵州桥吗?它是1300多年前我国隋代建造的石拱桥, 是我国古代人民勤劳与智慧的结晶.它的主桥是圆弧形,它的跨度(弧所对的弦的长)为37.4m, 拱高(弧的中点到弦的距离)为7.2m,你能求出赵洲桥主桥拱的半径吗? 赵州桥主桥拱的半径是多少? 问题情境可以发现:圆是轴对称图形,任何一条直径所在直线都是它的对称轴. 1. 圆的对称性: 不借助任何工具,你能找到圆形纸 片的圆心吗? 由此你能得到什么结论?如图,AB是⊙O的一条弦,作直径CD,使CD⊥AB,垂足为E.(1)这个图形是轴对称图形吗?如果是,它的对称轴是什么?(2)你能发现图中有哪些相等的线段和弧?为什么?·OABCDE(1)是轴对称图形.直径CD所在的直线是它的对称轴(2) 线段: AE=BE垂直于弦的直径平分这条弦, 并且平分弦所对的两条弧.垂径定理垂直于弦的直径平分弦,并且平分弦所对的两条弧CD⊥AB ∵ CD是直径,∴ AE=BE,·OABCDE归纳:下列图形是否具备垂径定理的条件?是不是是不是深化:垂径定理的几个基本图形:CD过圆心CD⊥AB于EAE=BE巩固:1、如图,AB是⊙O的直径,CD为弦,CD⊥AB于E,则下列结论中不成立的是( )A、∠COE=∠DOEB、CE=DEC、OE=AE2、如图,OE⊥AB于E,若⊙O的半径为10cm,OE=6cm,则AB= cm。·OABE解:连接OA,∵ OE⊥AB∴ AB=2AE=16cm3、如图,在⊙O中,弦AB的长为8cm,圆心O到AB的距离为3cm,求⊙O的半径。·OABE解:过点O作OE⊥AB于E,连接OA即⊙O的半径为5cm.弦心距:圆心到弦的距离圆心到弦的距离、半径、弦构成直角三角形,便将问题转化为直角三角形的问题。4、如图,CD是⊙O的直径,弦AB⊥CD于E,CE=1,AB=10,求直径CD的长。解:连接OA,∵ CD是直径,OE⊥AB设OA=x,则OE=x-1,由勾股定理得x2=52+(x-1)2解得:x=13∴ OA=13∴ CD=2OA=26即直径CD的长为26.证明:作直径MN⊥AB。 推论: 圆的两条平行弦所夹的弧相等. 如图:在⊙O中,设⊙O半径为R,弦AB=a,弦心距OD=d, 弓形的高DE=h, 且OE⊥AB于D. 己知求(1) R,da,h(3) R,ad,h(4) d,h R,a(2) R,ha,daRhdABODE(5) a,h R,d………归纳1300多年前, 我国隋代建造的赵州石拱桥的桥拱是圆弧形,它的跨度(弧所对的弦的长)为37.4米,拱高(弧的中点到弦的距离,也叫弓形高)为7.2米, 你能求出桥拱的半径吗?解决求赵州桥拱半径的问题你能利用垂径定理解决求赵州桥拱半径的问题吗?思考: 如图所示,在Rt△ABC中,∠C=900 ,AC=5cm,BC=12cm,以C为圆心,AC为半径的圆交斜边于D,求AD的长。猜想∴CD⊥ABOBCDE·如图,CD是⊙O的直径,AB为弦,
且AE=BE.A如何证明?探究:·OABCDE已知:如图,CD是⊙O的直径,AB为弦,且AE=BE.证明:连接OA,OB,则OA=OB∵ AE=BE∴ CD⊥AB此处的弦可以是直径吗?如果不能,请举出反例。 平分弦的直径垂直于弦,并且平分弦所对的两条弧。垂径定理推论 平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。∴ CD⊥AB, ∵ CD是直径, AE=BE·OABCDE新知:① CD是直径, ② CD⊥AB, ③ AM=BM 如果具备上面五个条件中的任何两个,根据圆的对称性,一定可以得到其他三个结论 一条直线满足:(1)过圆心;(2)垂直于弦;(3)平分弦(不是直径); (4)平分弦所对优弧;(5)平分弦所对的劣弧.只要具备上述五个条件中任两个,就可以推出其余三个.推广:1:判断下列说法的正误 ①平分弧的直径必平分弧所对的弦 ②平分弦的直线必垂直弦 ③垂直于弦的直径平分这条弦 ④平分弦的直径垂直于这条弦 ⑤弦的垂直平分线是圆的直径 ⑥平分弦所对的一条弧的直径必垂直这条弦 ⑦在圆中,如果一条直线经过圆心且平分弦,
必平分此弦所对的弧 ⑧圆是轴对称图形,直径是它的对称轴练习2、如图,有一段弧AB,你能用尺规将其平分吗?AB3. 如图,巳知:⊙O1与⊙O2相交于A,B两点, 且AB=8, 连结O1O2 , 则
O1O2⊥AB, 已知⊙O2的半径为5,
O1O2=4, 求⊙O1的半径.O1O2ABE5434. 巳知:AB为⊙O的直径,CD为弦,AE⊥CD,BF⊥CD,垂足分别为E、F. 求证:EC=DFF证明:过点O作OG⊥CD,根据垂径定理得:CG=GD 5 :如图,⊙O中CD是弦,AB是直径,AE⊥CD于E,BF⊥CD于F,求证:CE=DF。
且AE=BE.A如何证明?探究:·OABCDE已知:如图,CD是⊙O的直径,AB为弦,且AE=BE.证明:连接OA,OB,则OA=OB∵ AE=BE∴ CD⊥AB此处的弦可以是直径吗?如果不能,请举出反例。 平分弦的直径垂直于弦,并且平分弦所对的两条弧。垂径定理推论 平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。∴ CD⊥AB, ∵ CD是直径, AE=BE·OABCDE新知:① CD是直径, ② CD⊥AB, ③ AM=BM 如果具备上面五个条件中的任何两个,根据圆的对称性,一定可以得到其他三个结论 一条直线满足:(1)过圆心;(2)垂直于弦;(3)平分弦(不是直径); (4)平分弦所对优弧;(5)平分弦所对的劣弧.只要具备上述五个条件中任两个,就可以推出其余三个.推广:1:判断下列说法的正误 ①平分弧的直径必平分弧所对的弦 ②平分弦的直线必垂直弦 ③垂直于弦的直径平分这条弦 ④平分弦的直径垂直于这条弦 ⑤弦的垂直平分线是圆的直径 ⑥平分弦所对的一条弧的直径必垂直这条弦 ⑦在圆中,如果一条直线经过圆心且平分弦,
必平分此弦所对的弧 ⑧圆是轴对称图形,直径是它的对称轴练习2、如图,有一段弧AB,你能用尺规将其平分吗?AB3. 如图,巳知:⊙O1与⊙O2相交于A,B两点, 且AB=8, 连结O1O2 , 则
O1O2⊥AB, 已知⊙O2的半径为5,
O1O2=4, 求⊙O1的半径.O1O2ABE5434. 巳知:AB为⊙O的直径,CD为弦,AE⊥CD,BF⊥CD,垂足分别为E、F. 求证:EC=DFF证明:过点O作OG⊥CD,根据垂径定理得:CG=GD 5 :如图,⊙O中CD是弦,AB是直径,AE⊥CD于E,BF⊥CD于F,求证:CE=DF。
同课章节目录
