13.2.2用坐标表示轴对称(第二课时)同步测试(含答案)
文档属性
| 名称 | 13.2.2用坐标表示轴对称(第二课时)同步测试(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 188.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-11-03 16:03:58 | ||
图片预览

文档简介
13.2.2
用坐标表示轴对称
一.选择题(共8小题)
1.点(3,2)关于x轴的对称点为( )
A.
(3,﹣2)
B.
(﹣3,2)
C.
(﹣3,﹣2)
D.
(2,﹣3)
2.点P(﹣2,1)关于y轴对称的点的坐标为( )
A.
(﹣2,﹣1)
B.
(2,1)
C.
(2,﹣1)
D.
(﹣2,1)
3.已知点A(3x﹣6,4y+15),点B(5y,x)关于x轴对称,则x+y的值是( )
A.
0
B.[
9
C.
﹣6
D.
﹣12
4.已知两点的坐标分别是(﹣2,3)和(2,3),则下列情况:其中正确的有( )
①两点关于x轴对称
②两点关于y轴对称
③两点之间距离为4.
A.
3个
B.
2个
C.
1个
D.
0个
5.点A(a,4)、点B(3,b)关于x轴对称,则(a+b)2014的值为( )
A.
0
B.
﹣1
C.
1
D.
72010
6.平面直角坐标系中的点P(2﹣m,m)关于x轴的对称点在第四象限,则m的取值范围在数轴上可表示为( )
A.
B.
C.
D.
7.点(6,3)关于直线x=2的对称点为( )
A.
(﹣6,3)
B.
(6,﹣3)
C.
(﹣2,3)
D.
(﹣3,﹣3)
8.两个完全相同的三角形纸片,在平面直角坐标系中的摆放位置如图所示,点P与点P′是一对对应点,若点P的坐标为(a,b),则点P′的坐标为( )
A.
(﹣a,﹣b)
B.
(b,a)
C.
(3﹣a,﹣b)
D.
(b+3,a)
二.填空题(共12小题)
9.已知点P(6,3)关于原点的对称P1点的坐标是 _________ .
10.在平面直角坐标系中,点A关于y轴对称的点A′的坐标为(﹣2,7),则点A的坐标为 _________ .
11.已知点P(3,﹣1)关于y轴的对称点Q的坐标是(a+b,1﹣b),则ab的值为 _________ .
12.在直角坐标系中,如果点A沿x轴翻折后能够与点B(﹣1,2)重合,那么A、B两点之间的距离等于 _________ .
13.若|3a﹣2|+|b﹣3|=0,求P(a,b)关于y轴的对轴点P′的坐标为 _________ .
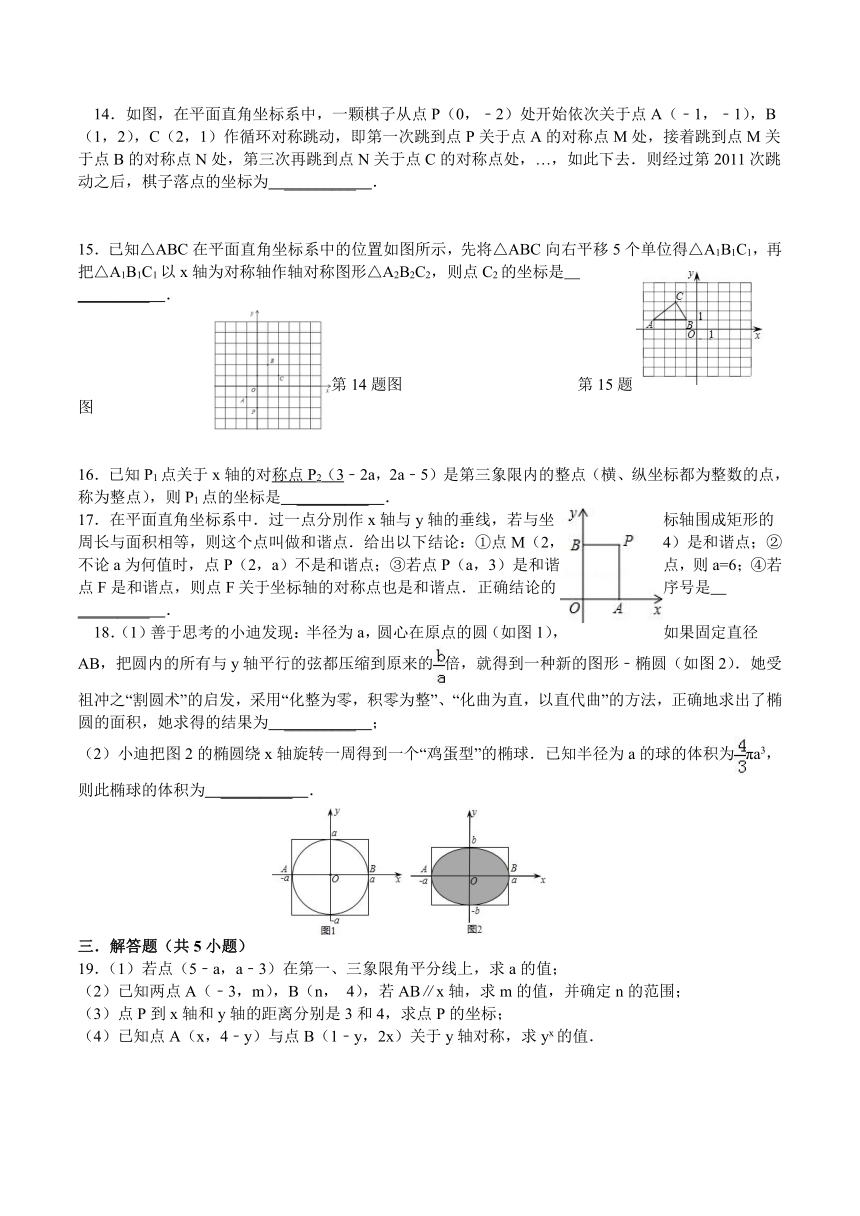
14.如图,在平面直角坐标系中,一颗棋子从点P(0,﹣2)处开始依次关于点A(﹣1,﹣1),B(1,2),C(2,1)作循环对称跳动,即第一次跳到点P关于点A的对称点M处,接着跳到点M关于点B的对称点N处,第三次再跳到点N关于点C的对称点处,…,如此下去.则经过第2011次跳动之后,棋子落点的坐标为 _________ .
15.已知△ABC在平面直角坐标系中的位置如图所示,先将△ABC向右平移5个单位得△A1B1C1,再把△A1B1C1以x轴为对称轴作轴对称图形△A2B2C2,则点C2的坐标是 _________ .
第14题图
第15题图
16.已知P1点关于x轴的对称点P2(3
( http: / / www.21cnjy.com )﹣2a,2a﹣5)是第三象限内的整点(横、纵坐标都为整数的点,称为整点),则P1点的坐标是 _________ .
17.在平面直角坐标系中.过一点分別作x轴与y轴的垂线,若与坐标轴围成矩形的周长与面积相等,则这个点叫做和谐点.给出以下结论:①点M(2,4)是和谐点;②不论a为何值时,点P(2,a)不是和谐点;③若点P(a,3)是和谐点,则a=6;④若点F是和谐点,则点F关于坐标轴的对称点也是和谐点.正确结论的序号是 _________ .
18.(1)善于思考的小迪发现:半径为a,圆心在原点的圆(如图1),如果固定直径AB,把圆内的所有与y轴平行的弦都压缩到原来的倍,就得到一种新的图形﹣椭圆(如图2).她受祖冲之“割圆术”的启发,采用“化整为零,积零为整”、“化曲为直,以直代曲”的方法,正确地求出了椭圆的面积,她求得的结果为 _________ ;
(2)小迪把图2的椭圆绕x轴旋转一周得到一个“鸡蛋型”的椭球.已知半径为a的球的体积为πa3,则此椭球的体积为 _________ .
三.解答题(共5小题)
19.(1)若点(5﹣a,a﹣3)在第一、三象限角平分线上,求a的值;
(2)已知两点A(﹣3,m),B(n,
4),若AB∥x轴,求m的值,并确定n的范围;
(3)点P到x轴和y轴的距离分别是3和4,求点P的坐标;
(4)已知点A(x,4﹣y)与点B(1﹣y,2x)关于y轴对称,求yx的值.
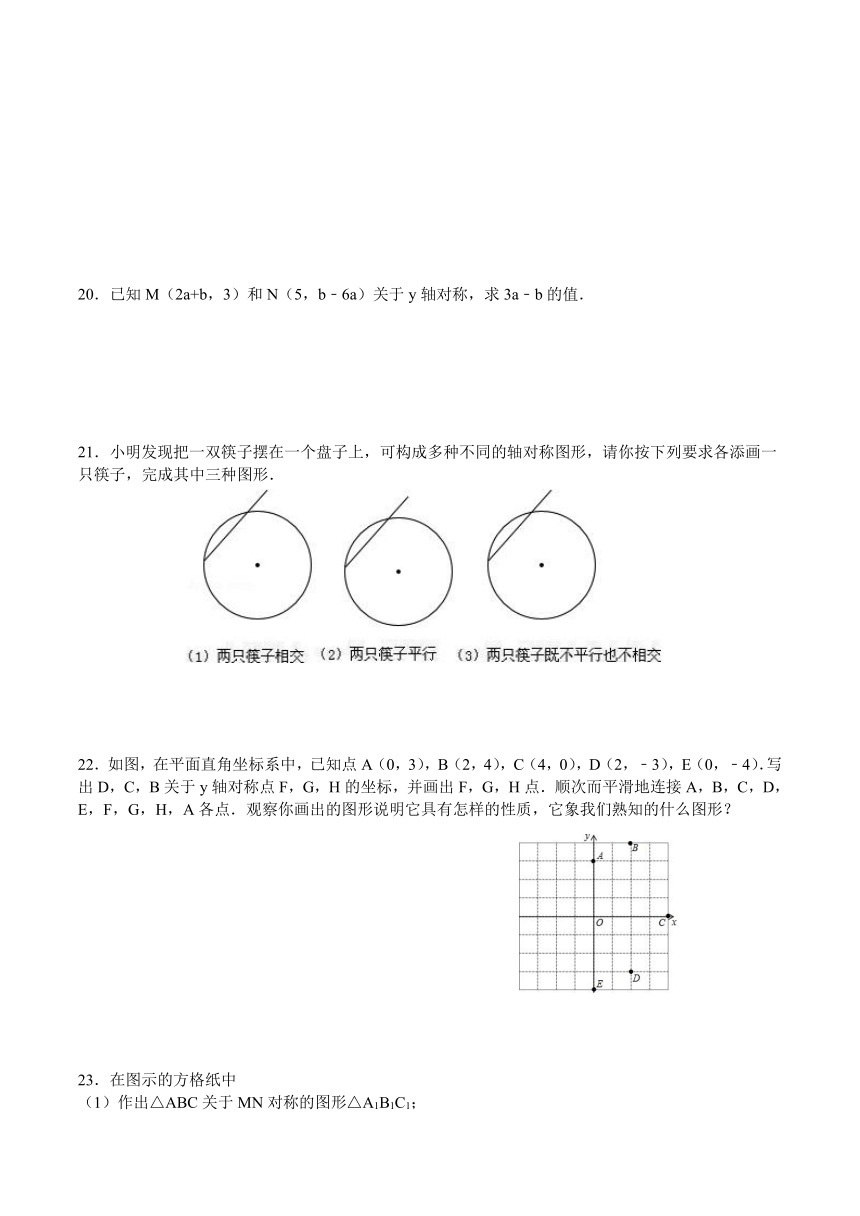
20.已知M(2a+b,3)和N(5,b﹣6a)关于y轴对称,求3a﹣b的值.
21.小明发现把一双筷子摆在一个盘子上,可构成多种不同的轴对称图形,请你按下列要求各添画一只筷子,完成其中三种图形.
22.如图,在平面直角坐标系中,已知点A(0,3),B(2,4),C(4,0),D(2,﹣3),E(0,﹣4).写出D,C,B关于y轴对称点F,G,H的坐标,并画出F,G,H点.顺次而平滑地连接A,B,C,D,E,F,G,H,A各点.观察你画出的图形说明它具有怎样的性质,它象我们熟知的什么图形?
23.在图示的方格纸中
(1)作出△ABC关于MN对称的图形△A1B1C1;
(2)说明△A2B2C2是由△A1B1C1经过怎样的平移得到的?
13.2.2
用坐标表示轴对称
一、选择题(共8小题)
1.A
2.B
3.C
4.B
5.C
6.B
7.C
8.C
二.填空题(共10小题)
9.(-6,-3)
10.(2,7)
11.
25
12.
4
13.
14.
(﹣2,0)
15.
(3,﹣3)
16.
(﹣1,1)
17.
②③④
18.
(1)πab (2)πab2
三.解答题(共5小题)
19.
解:(1)∵点(5﹣a,a﹣3)在第一、三象限角平分线上,
∴5﹣a=a﹣3,
解得:a=4;
(2)∵两点A(﹣3,m),B(n,4),AB∥x轴,
∴m=4,n≠3的任意实数;
(3)∵点P到x轴和y轴的距离分别是3和4,
∴P点可能在一、二、三、四象限,
∴点P的坐标为:(4,3),(﹣4,3),(﹣4,﹣3),(4,﹣3);
(4)∵点A(x,4﹣y)与点B(1﹣y,2x)关于y轴对称,
∴,
解得:,
∴yx=2.
20.
解:∵M(2a+b,3)和N(5,b﹣6a)关于y轴对称,
∴2a+b=﹣5,b﹣6a=3,
解得a=﹣1,b=﹣3,
∴3a﹣b=3×(﹣1)﹣(﹣3)=﹣3+3=0.
21.
解:
如图就是所求作的图形.
22.
解:由题意得,F(﹣2,﹣3),G(﹣4,0),H(﹣2,4),
( http: / / www.21cnjy.com )
这个图形关于y轴对称,是我们熟知的轴对称图形.
23.
解:(1)△A1B1C1如图所示;
(2)向右平移6个单位,再向下平移2个单位(或向下平移2个单位,再向右平移6个单位).
( http: / / www.21cnjy.com )
用坐标表示轴对称
一.选择题(共8小题)
1.点(3,2)关于x轴的对称点为( )
A.
(3,﹣2)
B.
(﹣3,2)
C.
(﹣3,﹣2)
D.
(2,﹣3)
2.点P(﹣2,1)关于y轴对称的点的坐标为( )
A.
(﹣2,﹣1)
B.
(2,1)
C.
(2,﹣1)
D.
(﹣2,1)
3.已知点A(3x﹣6,4y+15),点B(5y,x)关于x轴对称,则x+y的值是( )
A.
0
B.[
9
C.
﹣6
D.
﹣12
4.已知两点的坐标分别是(﹣2,3)和(2,3),则下列情况:其中正确的有( )
①两点关于x轴对称
②两点关于y轴对称
③两点之间距离为4.
A.
3个
B.
2个
C.
1个
D.
0个
5.点A(a,4)、点B(3,b)关于x轴对称,则(a+b)2014的值为( )
A.
0
B.
﹣1
C.
1
D.
72010
6.平面直角坐标系中的点P(2﹣m,m)关于x轴的对称点在第四象限,则m的取值范围在数轴上可表示为( )
A.
B.
C.
D.
7.点(6,3)关于直线x=2的对称点为( )
A.
(﹣6,3)
B.
(6,﹣3)
C.
(﹣2,3)
D.
(﹣3,﹣3)
8.两个完全相同的三角形纸片,在平面直角坐标系中的摆放位置如图所示,点P与点P′是一对对应点,若点P的坐标为(a,b),则点P′的坐标为( )
A.
(﹣a,﹣b)
B.
(b,a)
C.
(3﹣a,﹣b)
D.
(b+3,a)
二.填空题(共12小题)
9.已知点P(6,3)关于原点的对称P1点的坐标是 _________ .
10.在平面直角坐标系中,点A关于y轴对称的点A′的坐标为(﹣2,7),则点A的坐标为 _________ .
11.已知点P(3,﹣1)关于y轴的对称点Q的坐标是(a+b,1﹣b),则ab的值为 _________ .
12.在直角坐标系中,如果点A沿x轴翻折后能够与点B(﹣1,2)重合,那么A、B两点之间的距离等于 _________ .
13.若|3a﹣2|+|b﹣3|=0,求P(a,b)关于y轴的对轴点P′的坐标为 _________ .
14.如图,在平面直角坐标系中,一颗棋子从点P(0,﹣2)处开始依次关于点A(﹣1,﹣1),B(1,2),C(2,1)作循环对称跳动,即第一次跳到点P关于点A的对称点M处,接着跳到点M关于点B的对称点N处,第三次再跳到点N关于点C的对称点处,…,如此下去.则经过第2011次跳动之后,棋子落点的坐标为 _________ .
15.已知△ABC在平面直角坐标系中的位置如图所示,先将△ABC向右平移5个单位得△A1B1C1,再把△A1B1C1以x轴为对称轴作轴对称图形△A2B2C2,则点C2的坐标是 _________ .
第14题图
第15题图
16.已知P1点关于x轴的对称点P2(3
( http: / / www.21cnjy.com )﹣2a,2a﹣5)是第三象限内的整点(横、纵坐标都为整数的点,称为整点),则P1点的坐标是 _________ .
17.在平面直角坐标系中.过一点分別作x轴与y轴的垂线,若与坐标轴围成矩形的周长与面积相等,则这个点叫做和谐点.给出以下结论:①点M(2,4)是和谐点;②不论a为何值时,点P(2,a)不是和谐点;③若点P(a,3)是和谐点,则a=6;④若点F是和谐点,则点F关于坐标轴的对称点也是和谐点.正确结论的序号是 _________ .
18.(1)善于思考的小迪发现:半径为a,圆心在原点的圆(如图1),如果固定直径AB,把圆内的所有与y轴平行的弦都压缩到原来的倍,就得到一种新的图形﹣椭圆(如图2).她受祖冲之“割圆术”的启发,采用“化整为零,积零为整”、“化曲为直,以直代曲”的方法,正确地求出了椭圆的面积,她求得的结果为 _________ ;
(2)小迪把图2的椭圆绕x轴旋转一周得到一个“鸡蛋型”的椭球.已知半径为a的球的体积为πa3,则此椭球的体积为 _________ .
三.解答题(共5小题)
19.(1)若点(5﹣a,a﹣3)在第一、三象限角平分线上,求a的值;
(2)已知两点A(﹣3,m),B(n,
4),若AB∥x轴,求m的值,并确定n的范围;
(3)点P到x轴和y轴的距离分别是3和4,求点P的坐标;
(4)已知点A(x,4﹣y)与点B(1﹣y,2x)关于y轴对称,求yx的值.
20.已知M(2a+b,3)和N(5,b﹣6a)关于y轴对称,求3a﹣b的值.
21.小明发现把一双筷子摆在一个盘子上,可构成多种不同的轴对称图形,请你按下列要求各添画一只筷子,完成其中三种图形.
22.如图,在平面直角坐标系中,已知点A(0,3),B(2,4),C(4,0),D(2,﹣3),E(0,﹣4).写出D,C,B关于y轴对称点F,G,H的坐标,并画出F,G,H点.顺次而平滑地连接A,B,C,D,E,F,G,H,A各点.观察你画出的图形说明它具有怎样的性质,它象我们熟知的什么图形?
23.在图示的方格纸中
(1)作出△ABC关于MN对称的图形△A1B1C1;
(2)说明△A2B2C2是由△A1B1C1经过怎样的平移得到的?
13.2.2
用坐标表示轴对称
一、选择题(共8小题)
1.A
2.B
3.C
4.B
5.C
6.B
7.C
8.C
二.填空题(共10小题)
9.(-6,-3)
10.(2,7)
11.
25
12.
4
13.
14.
(﹣2,0)
15.
(3,﹣3)
16.
(﹣1,1)
17.
②③④
18.
(1)πab (2)πab2
三.解答题(共5小题)
19.
解:(1)∵点(5﹣a,a﹣3)在第一、三象限角平分线上,
∴5﹣a=a﹣3,
解得:a=4;
(2)∵两点A(﹣3,m),B(n,4),AB∥x轴,
∴m=4,n≠3的任意实数;
(3)∵点P到x轴和y轴的距离分别是3和4,
∴P点可能在一、二、三、四象限,
∴点P的坐标为:(4,3),(﹣4,3),(﹣4,﹣3),(4,﹣3);
(4)∵点A(x,4﹣y)与点B(1﹣y,2x)关于y轴对称,
∴,
解得:,
∴yx=2.
20.
解:∵M(2a+b,3)和N(5,b﹣6a)关于y轴对称,
∴2a+b=﹣5,b﹣6a=3,
解得a=﹣1,b=﹣3,
∴3a﹣b=3×(﹣1)﹣(﹣3)=﹣3+3=0.
21.
解:
如图就是所求作的图形.
22.
解:由题意得,F(﹣2,﹣3),G(﹣4,0),H(﹣2,4),
( http: / / www.21cnjy.com )
这个图形关于y轴对称,是我们熟知的轴对称图形.
23.
解:(1)△A1B1C1如图所示;
(2)向右平移6个单位,再向下平移2个单位(或向下平移2个单位,再向右平移6个单位).
( http: / / www.21cnjy.com )
