2.2等差数列1
图片预览




文档简介
课件19张PPT。复习回顾:1.数列定义:按照一定顺序排成的一列数简记作:{an}2.通项公式:如果数列{an}中第n项an与n之间的
关系可以用一个式子来表示,那么这
个公式叫做数列的通项公式.3.数列的分类(1)按项数分:项数有限的数列叫有穷数列(2)按项之间的大小关系:递增数列,递减数列,项数无限的数列叫无穷数列摆动数列,常数列。5.递推公式:4.数列的实质 数列可以看作是一个定义域为正整数集
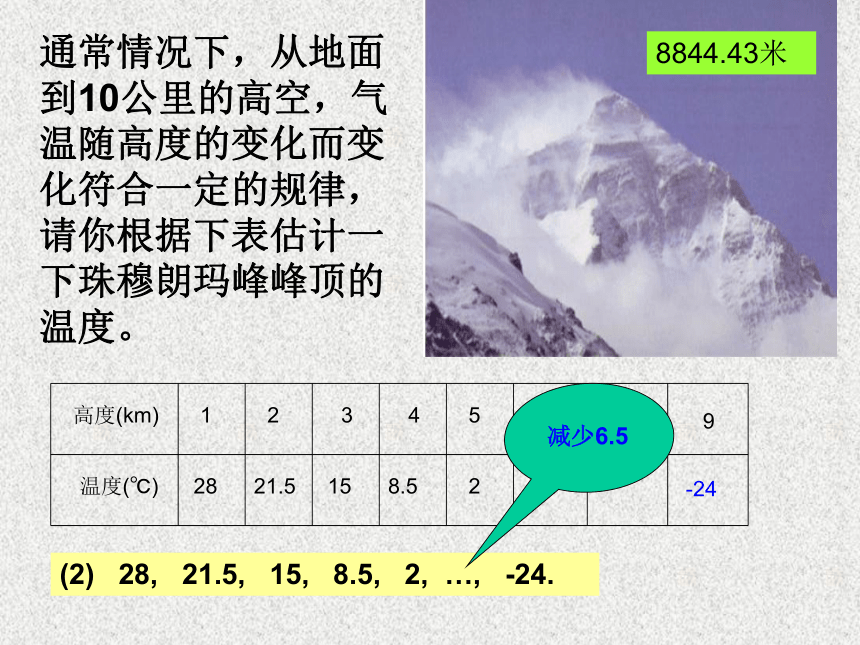
( 或它的有限子集{1,2,…,n})的函数,当自变量从小到大依 次取值时对应的一列函数值。 如果已知{an}的第1项(或前n项),且任一项an与它的前一项an-1(或前n项)间的关系可用一个公式来表示,这个公式叫做数列的递推公式.说明:递推公式也是数列的一种表示方法。§2.2等差数列(一)在过去的三百多年里,人们分别在下列时间里观测到了哈雷慧星:(1)1682,1758,1834,1910,1986,( )2062通常情况下,从地面到10公里的高空,气温随高度的变化而变化符合一定的规律,请你根据下表估计一下珠穆朗玛峰峰顶的温度。8844.43米9-24(2) 28, 21.5, 15, 8.5, 2, …, -24.减少6.5我国现行储蓄制度规定银行支付利息方式为单利,即不把利息加入本金计算下一期的利息.按照单利计算本利和的公式是:
本利和=本金×(1+利率×存期)
如按活期存入10000元,年利率是0.72%,那么按照单利,5年内各年末的本利和分别是: 1007210144102161028810360从0开始数数,每隔5数一次,可以得到数列:0,5,10,15, …( 3 ) 10072,10144,10216,10288,10360( 4 ) 0,5,10,15, … ( 1 ) 1682,1758,1834,1910,1986,(2062)( 2 ) 32, 25.5, 19, 12.5, 6, …, ( -24).它们的共同的规律是?共同特点:从第二项起,每一项与前一项的差都等于同一常数.1.等差数列的定义: 一般地,如果一个数列从第二项起,每一项与它的前一项的差等于同一个常数,那么这个数列就叫做等差数列. 这个常数叫做等差数列的公差,通常用字母
d表示.
注: (1)从第二项起; (2)同一个常数,且由后项减前项 可以表示为: an- an-1=d (d为常数,与n无关的数或者字母,n>1) 它们是等差数列吗?(6) 5,5,5,5,5,5,…公差 d=0 常数列公差 d= 2x(5) 1, 3, 5, 7, 9, 2, 4, 6, 8, 10× 在如下的两个数之间,插入一个什么数后这三个数就会成为一个等差数列:(1)2 ,( ) , 4 (2)-12,( ) ,0 3-6 如果在a与b中间插入一个数A,使a,A,b成等差数列,那么A叫做a与b的等差中项探究1( 3 ) , ( ) , 2.等差中项:(3) 1,4,7,10,13,16,…探究2:你会求该数列的通项公式吗?… …
等差数列的通项公式如果一个数列是等差数列,它的公差是d,那么 n=1时亦适合…迭加得…等差数列的通项公式3.等差数列的通项公式an=a1+(n-1)d a1为首项,d为公差注:1、等差数列的通项变形公式:an=am+(n-m)·d (m,n∈ N*) 2、知三求一例1 (1) 求等差数列8,5,2,…,的第20项。解:(2) 等差数列 -5,-9,-13,…,的第几项是 –401?解:因此,解得应用例2 在等差数列中,已知a5=10,a12=31,解:由题意可知 这是一个以 和 为未知数的二元一次方程组,解这个方程组,得即这个等差数列的首项是-2,公差是3.求首项a1与公差d.1. 求等差数列3,7,11,…的第4,7,10项;2. 100是不是等差数列2,9,16,…中的项?3. -20是不是等差数列0,- ,-7…中的项;练一练练一练4. 在等差数列中1、试用两种数学语言(文字语言、符号语言)来表述一下等差数列的概念:①如果一个数列从第2项起,每一项与它的前一项的差都等于同一个常数,那么这个数列叫做等差数列。 ②如果数列{an},满足an-an-1=d(d为常数,n≥2,且n∈N*),则数列{an}叫做以d为公差的等差数列。 2、首项是a1,公差是d的等差数列的通项公式为an=a1+(n-1)d,在a1,d,n,an这四个量中可知三求一,体现方程思想;总结反思3、等差数列的通项公式的推导方法——归纳法(由特殊到一般)和累加法,也是我们今后已知数列的递推式求通项公式的常用方法。4、数学与生活实际有着密切联系,数学概念来源于生活实际,又应用于生活实际
关系可以用一个式子来表示,那么这
个公式叫做数列的通项公式.3.数列的分类(1)按项数分:项数有限的数列叫有穷数列(2)按项之间的大小关系:递增数列,递减数列,项数无限的数列叫无穷数列摆动数列,常数列。5.递推公式:4.数列的实质 数列可以看作是一个定义域为正整数集
( 或它的有限子集{1,2,…,n})的函数,当自变量从小到大依 次取值时对应的一列函数值。 如果已知{an}的第1项(或前n项),且任一项an与它的前一项an-1(或前n项)间的关系可用一个公式来表示,这个公式叫做数列的递推公式.说明:递推公式也是数列的一种表示方法。§2.2等差数列(一)在过去的三百多年里,人们分别在下列时间里观测到了哈雷慧星:(1)1682,1758,1834,1910,1986,( )2062通常情况下,从地面到10公里的高空,气温随高度的变化而变化符合一定的规律,请你根据下表估计一下珠穆朗玛峰峰顶的温度。8844.43米9-24(2) 28, 21.5, 15, 8.5, 2, …, -24.减少6.5我国现行储蓄制度规定银行支付利息方式为单利,即不把利息加入本金计算下一期的利息.按照单利计算本利和的公式是:
本利和=本金×(1+利率×存期)
如按活期存入10000元,年利率是0.72%,那么按照单利,5年内各年末的本利和分别是: 1007210144102161028810360从0开始数数,每隔5数一次,可以得到数列:0,5,10,15, …( 3 ) 10072,10144,10216,10288,10360( 4 ) 0,5,10,15, … ( 1 ) 1682,1758,1834,1910,1986,(2062)( 2 ) 32, 25.5, 19, 12.5, 6, …, ( -24).它们的共同的规律是?共同特点:从第二项起,每一项与前一项的差都等于同一常数.1.等差数列的定义: 一般地,如果一个数列从第二项起,每一项与它的前一项的差等于同一个常数,那么这个数列就叫做等差数列. 这个常数叫做等差数列的公差,通常用字母
d表示.
注: (1)从第二项起; (2)同一个常数,且由后项减前项 可以表示为: an- an-1=d (d为常数,与n无关的数或者字母,n>1) 它们是等差数列吗?(6) 5,5,5,5,5,5,…公差 d=0 常数列公差 d= 2x(5) 1, 3, 5, 7, 9, 2, 4, 6, 8, 10× 在如下的两个数之间,插入一个什么数后这三个数就会成为一个等差数列:(1)2 ,( ) , 4 (2)-12,( ) ,0 3-6 如果在a与b中间插入一个数A,使a,A,b成等差数列,那么A叫做a与b的等差中项探究1( 3 ) , ( ) , 2.等差中项:(3) 1,4,7,10,13,16,…探究2:你会求该数列的通项公式吗?… …
等差数列的通项公式如果一个数列是等差数列,它的公差是d,那么 n=1时亦适合…迭加得…等差数列的通项公式3.等差数列的通项公式an=a1+(n-1)d a1为首项,d为公差注:1、等差数列的通项变形公式:an=am+(n-m)·d (m,n∈ N*) 2、知三求一例1 (1) 求等差数列8,5,2,…,的第20项。解:(2) 等差数列 -5,-9,-13,…,的第几项是 –401?解:因此,解得应用例2 在等差数列中,已知a5=10,a12=31,解:由题意可知 这是一个以 和 为未知数的二元一次方程组,解这个方程组,得即这个等差数列的首项是-2,公差是3.求首项a1与公差d.1. 求等差数列3,7,11,…的第4,7,10项;2. 100是不是等差数列2,9,16,…中的项?3. -20是不是等差数列0,- ,-7…中的项;练一练练一练4. 在等差数列中1、试用两种数学语言(文字语言、符号语言)来表述一下等差数列的概念:①如果一个数列从第2项起,每一项与它的前一项的差都等于同一个常数,那么这个数列叫做等差数列。 ②如果数列{an},满足an-an-1=d(d为常数,n≥2,且n∈N*),则数列{an}叫做以d为公差的等差数列。 2、首项是a1,公差是d的等差数列的通项公式为an=a1+(n-1)d,在a1,d,n,an这四个量中可知三求一,体现方程思想;总结反思3、等差数列的通项公式的推导方法——归纳法(由特殊到一般)和累加法,也是我们今后已知数列的递推式求通项公式的常用方法。4、数学与生活实际有着密切联系,数学概念来源于生活实际,又应用于生活实际
