2.2等差数列2
图片预览




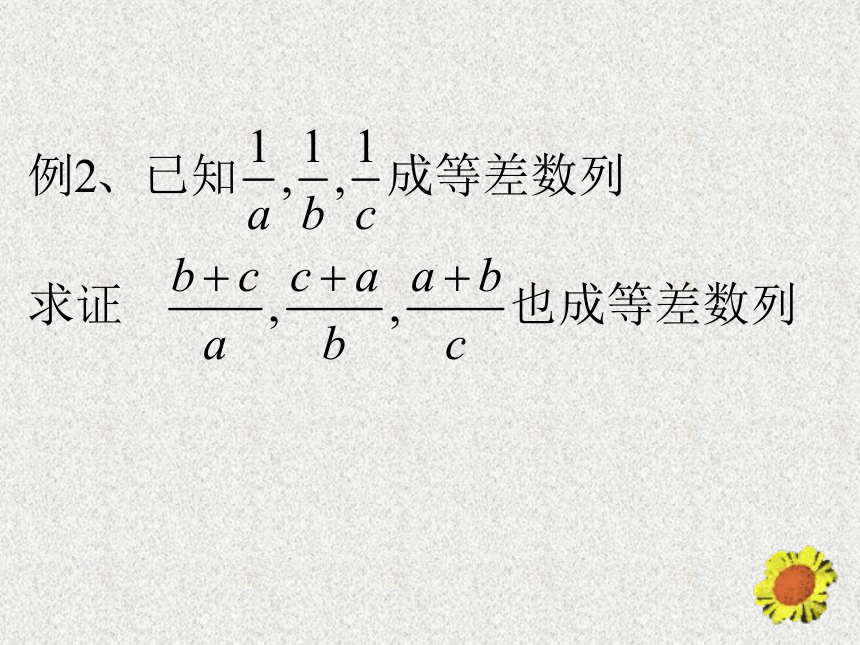
文档简介
课件14张PPT。§2.2等差数列(二)一.复习
1.等差数列的定义: 如果一个数列从第二
项起,每一项与前一项的差等于同一个常数.则这个数列叫做等差数列2.等差中项:如果a,A,b成等差数列,那么A叫做a与b的等差中项3.通项公式:4.公式变形:an=am+(n-m)·d (m,n∈ N*)5.d的计算方法6.判断等差数列的方法:1)、(定义法)利用an-an-1是否是一个与n无关的常数2)、(中项公式法)判断an与an+1+an-1的关系1、 已知三个数成等差数列,其和为15,其平方和
为83,求此三个数?分析: 这三个数可设为 a, a+d, a+2d或者 a-d, a, a+d
解答 设此三数分别为 a-d, a, a+d
则有 (a-d)+a+(a+d)=15
(a-d)2+a2+(a+d)2=83
解得 a=5 d=2 或 a=5 d= - 2
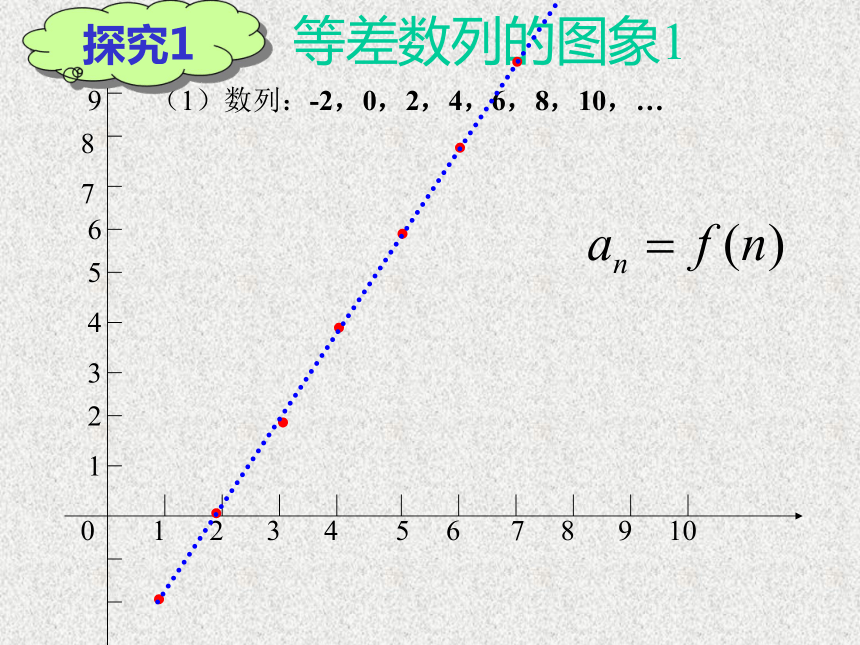
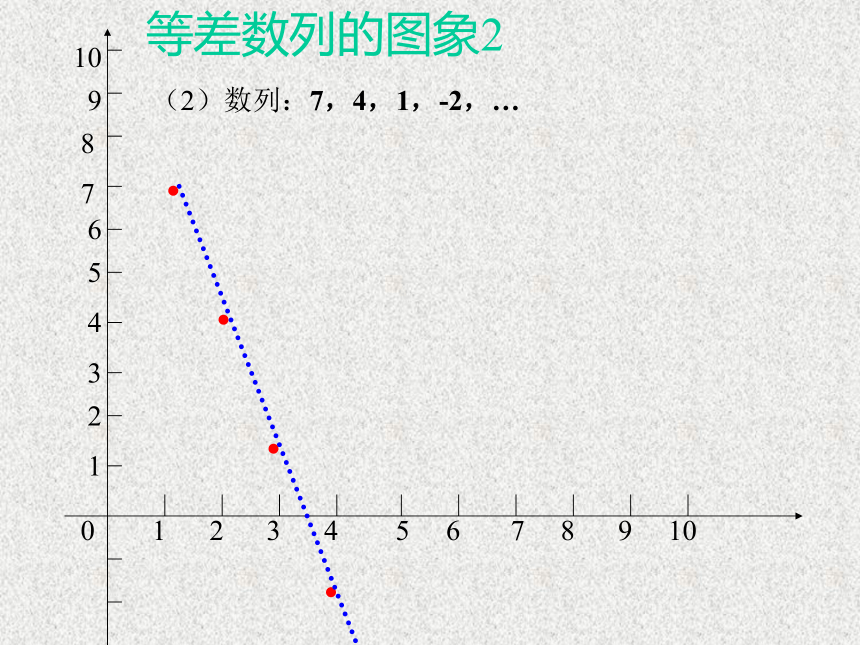
所求三个数分别为 3,5,7 或 7,5,3练习:等差数列的图象1(1)数列:-2,0,2,4,6,8,10,…●●●●●●●探究1等差数列的图象2(2)数列:7,4,1,-2,…●●●●等差数列的图象3(3)数列:4,4,4,4,4,4,4,…●●●●●●●●●●已知数列{an} 通项公式为an=pn+q (p、q是常数),那么这个数列一定是等差数列吗?探究2直线的一般形式:等差数列的通项公式为:结论:等差数列的图象为相应
直线上的点.练习:证明数列 是等差数列?3、(通项公式法)判断an=pn+q(p、q为常数)性质: 在等差数列 中, 为公差,
若 且
那么: 推论: 在等差数列中,与首末两项距离相
等的两项和等于首末两项的和,即等差数列的性质例1:在等差数列{an}中,
(1). a2+a3+a23+a24=48 ,求a13(2).a2+a3+a4+a5=34, a2·a5=52,求公差d例题分析例2:梯子的最高一级宽33cm,最低一级宽110cm,中间还有10级.各级的宽度成等差数列,计算中间各级的宽度.等差数列的应用点评:用等差数列解决实际问题的步骤:分析题意构建等差数列模型求解等差数列完成实际问题解答1、试用两种数学语言(文字语言、符号语言、图象语言)来表述一下等差数列的概念:①如果一个数列从第2项起,每一项与它的前一项的差都等于同一个常数,那么这个数列叫做等差数列。 ②如果数列{an},满足an-an-1=d(d为常数,n≥2,且n∈N*),则数列{an}叫做以d为公差的等差数列。 2、首项是a1,公差是d的等差数列的通项公式为an=a1+(n-1)d,在a1,d,n,an这四个量中可知三求一,体现方程思想;总结反思3、等差数列的通项公式的推导方法——迭代法和累加法,也是我们今后已知数列的递推式求通项公式的常用方法。4、数学与生活实际有着密切联系,数学概念来源于生活实际,又应用于生活实际
1.等差数列的定义: 如果一个数列从第二
项起,每一项与前一项的差等于同一个常数.则这个数列叫做等差数列2.等差中项:如果a,A,b成等差数列,那么A叫做a与b的等差中项3.通项公式:4.公式变形:an=am+(n-m)·d (m,n∈ N*)5.d的计算方法6.判断等差数列的方法:1)、(定义法)利用an-an-1是否是一个与n无关的常数2)、(中项公式法)判断an与an+1+an-1的关系1、 已知三个数成等差数列,其和为15,其平方和
为83,求此三个数?分析: 这三个数可设为 a, a+d, a+2d或者 a-d, a, a+d
解答 设此三数分别为 a-d, a, a+d
则有 (a-d)+a+(a+d)=15
(a-d)2+a2+(a+d)2=83
解得 a=5 d=2 或 a=5 d= - 2
所求三个数分别为 3,5,7 或 7,5,3练习:等差数列的图象1(1)数列:-2,0,2,4,6,8,10,…●●●●●●●探究1等差数列的图象2(2)数列:7,4,1,-2,…●●●●等差数列的图象3(3)数列:4,4,4,4,4,4,4,…●●●●●●●●●●已知数列{an} 通项公式为an=pn+q (p、q是常数),那么这个数列一定是等差数列吗?探究2直线的一般形式:等差数列的通项公式为:结论:等差数列的图象为相应
直线上的点.练习:证明数列 是等差数列?3、(通项公式法)判断an=pn+q(p、q为常数)性质: 在等差数列 中, 为公差,
若 且
那么: 推论: 在等差数列中,与首末两项距离相
等的两项和等于首末两项的和,即等差数列的性质例1:在等差数列{an}中,
(1). a2+a3+a23+a24=48 ,求a13(2).a2+a3+a4+a5=34, a2·a5=52,求公差d例题分析例2:梯子的最高一级宽33cm,最低一级宽110cm,中间还有10级.各级的宽度成等差数列,计算中间各级的宽度.等差数列的应用点评:用等差数列解决实际问题的步骤:分析题意构建等差数列模型求解等差数列完成实际问题解答1、试用两种数学语言(文字语言、符号语言、图象语言)来表述一下等差数列的概念:①如果一个数列从第2项起,每一项与它的前一项的差都等于同一个常数,那么这个数列叫做等差数列。 ②如果数列{an},满足an-an-1=d(d为常数,n≥2,且n∈N*),则数列{an}叫做以d为公差的等差数列。 2、首项是a1,公差是d的等差数列的通项公式为an=a1+(n-1)d,在a1,d,n,an这四个量中可知三求一,体现方程思想;总结反思3、等差数列的通项公式的推导方法——迭代法和累加法,也是我们今后已知数列的递推式求通项公式的常用方法。4、数学与生活实际有着密切联系,数学概念来源于生活实际,又应用于生活实际
