2.3等差数列的前n项和(1)
文档属性
| 名称 | 2.3等差数列的前n项和(1) |  | |
| 格式 | rar | ||
| 文件大小 | 252.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-05-20 09:26:00 | ||
图片预览






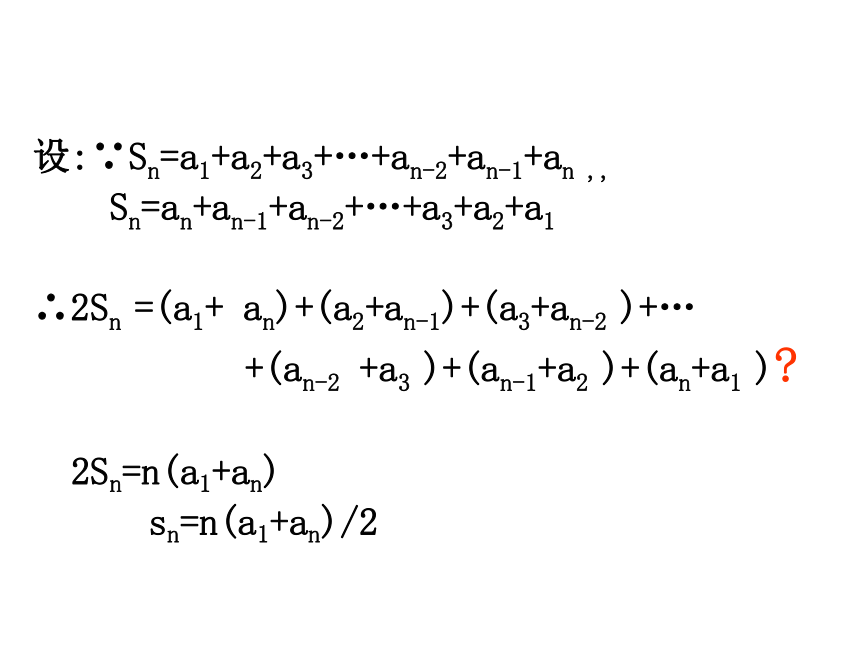
文档简介
课件15张PPT。学习目标:1、掌握等差数列前n项和公式及其推导过程;2、初步掌握公式的简单运用。教学重点、难点:重点是等差数列前n项和公式,难点是获得推导公式的思路。[克服难点的关键 是通过具体例子发现一般规律]前提检测:(1)什么叫等差数列?(2)数列“1,2,3,…,n,…”是等差数列吗?为什么?(3)等差数列的通项公式是什么?如果一个数列从第2项起,每一项与它前一项的差等于同一个常数,那么这个数列就叫做等差数列.其形式化表示为:an=a1+(n-1)d一、等差数列前n项和的引入:1、引例:1+2+3+…+100=?2、高斯的算法:
首项与末项的和:1+100=101,
第2项与倒数第2项的和:2+99=101,
第3项与倒数第3项的和:3+98=101,
……
第50项与倒数第50项的和:50+51=101.
于是所求的和为:高斯,德国著名数学家。3、上述求解过程带给我们什么启示?(1)所求的和可以用首项、末项及公差来表示;
(2)任意的第k项与倒数第k项的和都等于首项与末项的和。解法2:设:∵S= 1+2+3+4+···+97+98+99+100 ,
S=100+99+98+97+···+4+3+2+1 ,
∴2S=(1+100)+(2+99)+(3+98)+(4+97)+ ···(97+4)+(98+3)
+(99+2)+(100+1)
=100×101
s=100×(1+100)/2
∴S=5050
注:此法称倒序求和(属代数法)二、等差数列前n项和公式的推导:设等差数列{an}的前n项和为sn
an=a1+n(n-1)d设:∵Sn=a1+a2+a3+…+an-2+an-1+an ,,
Sn=an+an-1+an-2+…+a3+a2+a1
∴2Sn =(a1+ an)+(a2+an-1)+(a3+an-2 )+…
+(an-2 +a3 )+(an-1+a2 )+(an+a1 )?
2Sn=n(a1+an)
sn=n(a1+an)/2解决疑难问题定理 :数列{an}是等差数列,m,n,p,q分别为自然数 若m+n=p+q,则am+an=ap+aq.
证明:设等差数列首项为a1,公差为d,则
am+an=a1+(m-1)d+a1+(n-1 )d
=2a1+(m+n-2)d
ap+aq=a1+(p-1)d+a1+(q-1)d
= 2a1+(p+q-2)d
∵ m+n=p+q, ∴ m+n-2=p+q-2
∴ am+an=ap+aq2.公式记忆 用梯形面积公式记忆等差数列前 项和公式,这里对图形进行了割、补两种处理,对应着等差数列前 项和的两个公式.三、应用举例:1、一个堆放铅笔的V形架的最下面一层放一支铅笔,往上每一层都比它下面一层多放一支,最上面一层放120支。这个V形架上共放着多少支铅笔?解:由题意可知,这个V形架上共放着120层铅笔,且自下而上各层的铅笔数成等差数列,将其记为{an},则有a1=1, a120=120.根据等差数列前n项和的公式:答:V形架上共放着7260支铅笔。三、应用举例:2、等差数列-10,-6,-2,2,...前多少项和是54?解:将题中的等差数列记为{an},sn代表该数列 的前n项和,则有a1=-10, d=-6-(-10)=4
设该数列前n 项和为54 根据等差数列前n项和公式:
解得 n1=9, n2=-3(舍去)因此等差数列-10,-6,-2,2,...前9项的和是54.四、随堂练习1、根据下列各题中的条件,求相应的等差数列{an}的sn(1)a1=5,an=95,n=10(2)a1=100,d=-2,n=50(3)a1=14.5,d=0.7,an=322、(1)求正整数列中前n个数的和;
(2)求正整数列中前n个偶数的和。3、等差数列5,4,3,2,1,…前多少项的和是-30?[前15项]小结 一、等差数列的前n项和公式
Sn=na1+n(n-1)d/2
Sn=n[a1+ an ]/2
二、运用和应用
(1)函数思想 (2)方程思想
(3)数学应用思想(4)倒序求和法
三、数学发现的方法
学会猜想,学会证明 .
五、作业及课外练习:1、作业:P46习题2.3第1、3、4题。2、课外练习:P46习题3.3第2题。
首项与末项的和:1+100=101,
第2项与倒数第2项的和:2+99=101,
第3项与倒数第3项的和:3+98=101,
……
第50项与倒数第50项的和:50+51=101.
于是所求的和为:高斯,德国著名数学家。3、上述求解过程带给我们什么启示?(1)所求的和可以用首项、末项及公差来表示;
(2)任意的第k项与倒数第k项的和都等于首项与末项的和。解法2:设:∵S= 1+2+3+4+···+97+98+99+100 ,
S=100+99+98+97+···+4+3+2+1 ,
∴2S=(1+100)+(2+99)+(3+98)+(4+97)+ ···(97+4)+(98+3)
+(99+2)+(100+1)
=100×101
s=100×(1+100)/2
∴S=5050
注:此法称倒序求和(属代数法)二、等差数列前n项和公式的推导:设等差数列{an}的前n项和为sn
an=a1+n(n-1)d设:∵Sn=a1+a2+a3+…+an-2+an-1+an ,,
Sn=an+an-1+an-2+…+a3+a2+a1
∴2Sn =(a1+ an)+(a2+an-1)+(a3+an-2 )+…
+(an-2 +a3 )+(an-1+a2 )+(an+a1 )?
2Sn=n(a1+an)
sn=n(a1+an)/2解决疑难问题定理 :数列{an}是等差数列,m,n,p,q分别为自然数 若m+n=p+q,则am+an=ap+aq.
证明:设等差数列首项为a1,公差为d,则
am+an=a1+(m-1)d+a1+(n-1 )d
=2a1+(m+n-2)d
ap+aq=a1+(p-1)d+a1+(q-1)d
= 2a1+(p+q-2)d
∵ m+n=p+q, ∴ m+n-2=p+q-2
∴ am+an=ap+aq2.公式记忆 用梯形面积公式记忆等差数列前 项和公式,这里对图形进行了割、补两种处理,对应着等差数列前 项和的两个公式.三、应用举例:1、一个堆放铅笔的V形架的最下面一层放一支铅笔,往上每一层都比它下面一层多放一支,最上面一层放120支。这个V形架上共放着多少支铅笔?解:由题意可知,这个V形架上共放着120层铅笔,且自下而上各层的铅笔数成等差数列,将其记为{an},则有a1=1, a120=120.根据等差数列前n项和的公式:答:V形架上共放着7260支铅笔。三、应用举例:2、等差数列-10,-6,-2,2,...前多少项和是54?解:将题中的等差数列记为{an},sn代表该数列 的前n项和,则有a1=-10, d=-6-(-10)=4
设该数列前n 项和为54 根据等差数列前n项和公式:
解得 n1=9, n2=-3(舍去)因此等差数列-10,-6,-2,2,...前9项的和是54.四、随堂练习1、根据下列各题中的条件,求相应的等差数列{an}的sn(1)a1=5,an=95,n=10(2)a1=100,d=-2,n=50(3)a1=14.5,d=0.7,an=322、(1)求正整数列中前n个数的和;
(2)求正整数列中前n个偶数的和。3、等差数列5,4,3,2,1,…前多少项的和是-30?[前15项]小结 一、等差数列的前n项和公式
Sn=na1+n(n-1)d/2
Sn=n[a1+ an ]/2
二、运用和应用
(1)函数思想 (2)方程思想
(3)数学应用思想(4)倒序求和法
三、数学发现的方法
学会猜想,学会证明 .
五、作业及课外练习:1、作业:P46习题2.3第1、3、4题。2、课外练习:P46习题3.3第2题。
