2.4等比数列
图片预览







文档简介
(共30张PPT)
一、温故知新:
1、等差数列定义:
2、等差数列单调性:
an-an-1=d(d为常数)
d>0单调递增
d<0单调递减
d=0常数列
用什么方法如推出的呢?图像怎样?
要点扫描:
本节课主要学习
①等比数列的定义:“从第2项起,后项与前一项比为常数”。
②通项公式: an = a1 qn-1
及推导
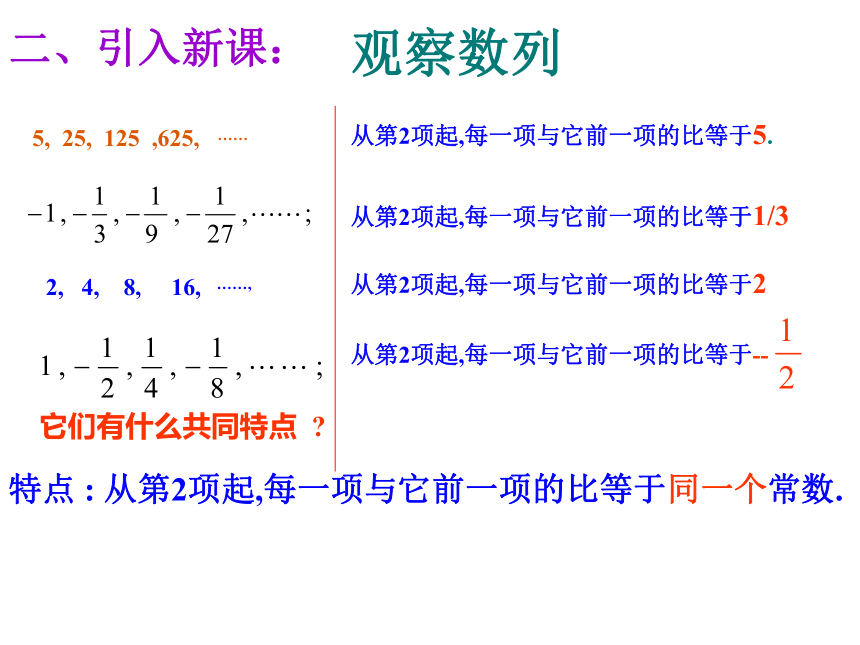
5, 25, 125 ,625, ……
2, 4, 8, 16, ……,
它们有什么共同特点
特点 : 从第2项起,每一项与它前一项的比等于同一个常数.
观察数列
从第2项起,每一项与它前一项的比等于5.
从第2项起,每一项与它前一项的比等于2
从第2项起,每一项与它前一项的比等于--
从第2项起,每一项与它前一项的比等于1/3
二、引入新课:
1.等比数列定义:
如果一个数列从第2项起,每一项与它前一项的比等于同一个常数,那么,这个数列就叫做等比数列.
这个常数叫做等比数列的公比,公比通常用字母q表示(q 不等于0)。
数学语言:an : an-1 = q
(q是常数且不为0,n≥2,n∈N*)
记忆
问:数列a, a, a, a, …(a∈R)是否为等比数列?
如果是,a必须满足什么条件?
(1) a=0; 它只是等差数列。
(2) a≠0; 它既是等差数列又是等比数列。
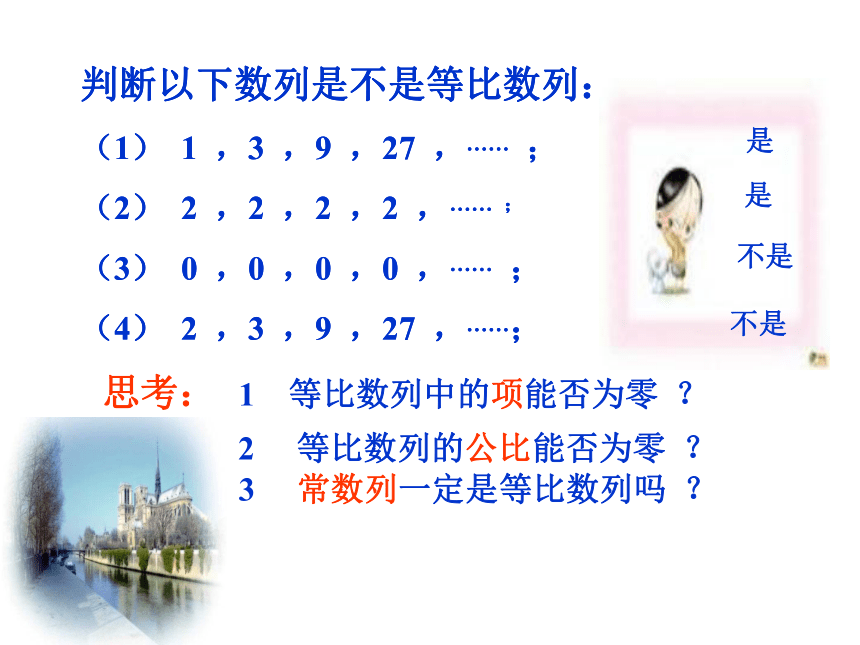
判断以下数列是不是等比数列:
(1) 1 ,3 ,9 ,27 ,…… ;
(2) 2 ,2 ,2 ,2 ,…… ;
(3) 0 ,0 ,0 ,0 ,…… ;
(4) 2 ,3 ,9 ,27 ,……;
思考: 1 等比数列中的项能否为零 ?
2 等比数列的公比能否为零 ?
3 常数列一定是等比数列吗 ?
判断以下数列是不是等比数列:
(1) 1 ,3 ,9 ,27 ,…… ;
(2) 2 ,2 ,2 ,2 ,…… ;
(3) 0 ,0 ,0 ,0 ,…… ;
(4) 2 ,3 ,9 ,27 ,……;
是
是
不是
不是
注:对定义的认识
1.等比数列的首项不为0, 即a1≠0。
2.等比数列的每一项都不为0,即an≠0。
3.公比不为0,即q≠0。
在等比数列{an}中 ,首项为a1 ,公比为q,那么数列中的各项能不能用a1和q来表示 ?
a2=a1q
a3=a2q
= a1q2
a4=a3q
= a1q3
……………………
a10=
a1q9
猜想:an=
a1qn-1
当n=1时,上式也成立
等比数列的通项公式 :an=a1qn-1
a2 : a1 = q
a3 : a2 = q
a4 : a3 = q
……
an-1 : an-2 = q
an : an-1 = q
这(n-1)个式子迭乘
an : a1 = qn-1
a2=a1q
a3=a2q=a1q2
a4=a3q=a1q3
……
由此得到 an = a1qn-1
等比数列的通项公式 : an = a1 qn-1
2、等比中项
观察如下的两个数之间,插入一个什么数后者三个数就会成为一个等比数列:
(1)1, , 9 (2)-1, ,-4
(3)-12, ,-3 (4)1, ,1
±3
±2
±6
±1
如果在a与b中间插入一个数G,使a,G,b成等比数列,那么G叫做a与b的等比中项。
q>1 0递增
递减
常数列
递增
递减
常数列
分类:
a1<0
a1>0
练习 :
(1) 已知 a1=2 ,q=2 ,求a10
(2) 已知 a10=2-10 ,a1= ,求q
(3) 已知 a1=2 ,q= ,an=210 ,求 n
(4)已知 a10=310 ,q= , 求a1
答案:(1)a10=______ (2)q=_____
(3)n=______ (4)a1=_____
1024
319
18
例1 某农科小组培育水稻新品种,如果第一代得到120粒种子,并且从第一代起,由以后各代的每一粒种子都可以得到下一代的120粒种子,到第5代大约可以得到这个新品种的种子多少粒(保留两个有效数字)?
解 :由于每代的种子数是它的前一代种子数的120倍
所以,逐代的种子数组成一个等比数列,记为{an},
其中 a1=120 ,q=120
所以 a5=a1q4=120×1204≈2.5×1010
答 :到第5代大约可以得到种子2.5×1010粒。
例2 一个等比数列的第3项与第4项分别是12与18
求它的第1项与第2项.
解:设这个等比数列的第1项是a1,公比是q,则: 12=a1q2 18=a1q3
所以 a1=16/3 q=3/2 a2=8
答:这个数列的第1项与第2项分别为16/3 与8。
变式练习 :如果已知等比数列{an}中的a3=8 ,a5=32, 求 a1与q。
结论:如果 是项数相同的等比数列,那么 也是等比数列.
证明:设数列 的公比为p, 的公比为q,那么数列 的第n项与第n+1项分别为 与 ,即 与 .
因为
它是一个与n无关的常数,所以是一个以pq为公比的等比数列.
特别地,如果是 等比数列,c是不等于0的常数,那么数列 也是等比数列.
探究
对于例4中的等比数列 与 ,数
列 也一定是等比数列吗?
是
知识拓展
一、通项公式的推广
4、等比数列所有奇数项符号相同;
所有偶数项符号相同。
二、等比数列的性质
定义法:
三、判断等比数列的方法
中项法:
三个数a,b,c成等比数列
1.定义
2.公比(差)
3.等比(差)
中项
4.通项公式
5.性质
(若m+n=p+q)
q不可以是0,
d可以是0
等比中项
等差中项
等差数列
等比数列
一、温故知新:
1、等差数列定义:
2、等差数列单调性:
an-an-1=d(d为常数)
d>0单调递增
d<0单调递减
d=0常数列
用什么方法如推出的呢?图像怎样?
要点扫描:
本节课主要学习
①等比数列的定义:“从第2项起,后项与前一项比为常数”。
②通项公式: an = a1 qn-1
及推导
5, 25, 125 ,625, ……
2, 4, 8, 16, ……,
它们有什么共同特点
特点 : 从第2项起,每一项与它前一项的比等于同一个常数.
观察数列
从第2项起,每一项与它前一项的比等于5.
从第2项起,每一项与它前一项的比等于2
从第2项起,每一项与它前一项的比等于--
从第2项起,每一项与它前一项的比等于1/3
二、引入新课:
1.等比数列定义:
如果一个数列从第2项起,每一项与它前一项的比等于同一个常数,那么,这个数列就叫做等比数列.
这个常数叫做等比数列的公比,公比通常用字母q表示(q 不等于0)。
数学语言:an : an-1 = q
(q是常数且不为0,n≥2,n∈N*)
记忆
问:数列a, a, a, a, …(a∈R)是否为等比数列?
如果是,a必须满足什么条件?
(1) a=0; 它只是等差数列。
(2) a≠0; 它既是等差数列又是等比数列。
判断以下数列是不是等比数列:
(1) 1 ,3 ,9 ,27 ,…… ;
(2) 2 ,2 ,2 ,2 ,…… ;
(3) 0 ,0 ,0 ,0 ,…… ;
(4) 2 ,3 ,9 ,27 ,……;
思考: 1 等比数列中的项能否为零 ?
2 等比数列的公比能否为零 ?
3 常数列一定是等比数列吗 ?
判断以下数列是不是等比数列:
(1) 1 ,3 ,9 ,27 ,…… ;
(2) 2 ,2 ,2 ,2 ,…… ;
(3) 0 ,0 ,0 ,0 ,…… ;
(4) 2 ,3 ,9 ,27 ,……;
是
是
不是
不是
注:对定义的认识
1.等比数列的首项不为0, 即a1≠0。
2.等比数列的每一项都不为0,即an≠0。
3.公比不为0,即q≠0。
在等比数列{an}中 ,首项为a1 ,公比为q,那么数列中的各项能不能用a1和q来表示 ?
a2=a1q
a3=a2q
= a1q2
a4=a3q
= a1q3
……………………
a10=
a1q9
猜想:an=
a1qn-1
当n=1时,上式也成立
等比数列的通项公式 :an=a1qn-1
a2 : a1 = q
a3 : a2 = q
a4 : a3 = q
……
an-1 : an-2 = q
an : an-1 = q
这(n-1)个式子迭乘
an : a1 = qn-1
a2=a1q
a3=a2q=a1q2
a4=a3q=a1q3
……
由此得到 an = a1qn-1
等比数列的通项公式 : an = a1 qn-1
2、等比中项
观察如下的两个数之间,插入一个什么数后者三个数就会成为一个等比数列:
(1)1, , 9 (2)-1, ,-4
(3)-12, ,-3 (4)1, ,1
±3
±2
±6
±1
如果在a与b中间插入一个数G,使a,G,b成等比数列,那么G叫做a与b的等比中项。
q>1 0
递减
常数列
递增
递减
常数列
分类:
a1<0
a1>0
练习 :
(1) 已知 a1=2 ,q=2 ,求a10
(2) 已知 a10=2-10 ,a1= ,求q
(3) 已知 a1=2 ,q= ,an=210 ,求 n
(4)已知 a10=310 ,q= , 求a1
答案:(1)a10=______ (2)q=_____
(3)n=______ (4)a1=_____
1024
319
18
例1 某农科小组培育水稻新品种,如果第一代得到120粒种子,并且从第一代起,由以后各代的每一粒种子都可以得到下一代的120粒种子,到第5代大约可以得到这个新品种的种子多少粒(保留两个有效数字)?
解 :由于每代的种子数是它的前一代种子数的120倍
所以,逐代的种子数组成一个等比数列,记为{an},
其中 a1=120 ,q=120
所以 a5=a1q4=120×1204≈2.5×1010
答 :到第5代大约可以得到种子2.5×1010粒。
例2 一个等比数列的第3项与第4项分别是12与18
求它的第1项与第2项.
解:设这个等比数列的第1项是a1,公比是q,则: 12=a1q2 18=a1q3
所以 a1=16/3 q=3/2 a2=8
答:这个数列的第1项与第2项分别为16/3 与8。
变式练习 :如果已知等比数列{an}中的a3=8 ,a5=32, 求 a1与q。
结论:如果 是项数相同的等比数列,那么 也是等比数列.
证明:设数列 的公比为p, 的公比为q,那么数列 的第n项与第n+1项分别为 与 ,即 与 .
因为
它是一个与n无关的常数,所以是一个以pq为公比的等比数列.
特别地,如果是 等比数列,c是不等于0的常数,那么数列 也是等比数列.
探究
对于例4中的等比数列 与 ,数
列 也一定是等比数列吗?
是
知识拓展
一、通项公式的推广
4、等比数列所有奇数项符号相同;
所有偶数项符号相同。
二、等比数列的性质
定义法:
三、判断等比数列的方法
中项法:
三个数a,b,c成等比数列
1.定义
2.公比(差)
3.等比(差)
中项
4.通项公式
5.性质
(若m+n=p+q)
q不可以是0,
d可以是0
等比中项
等差中项
等差数列
等比数列
