直线的倾斜角与斜率
图片预览



文档简介
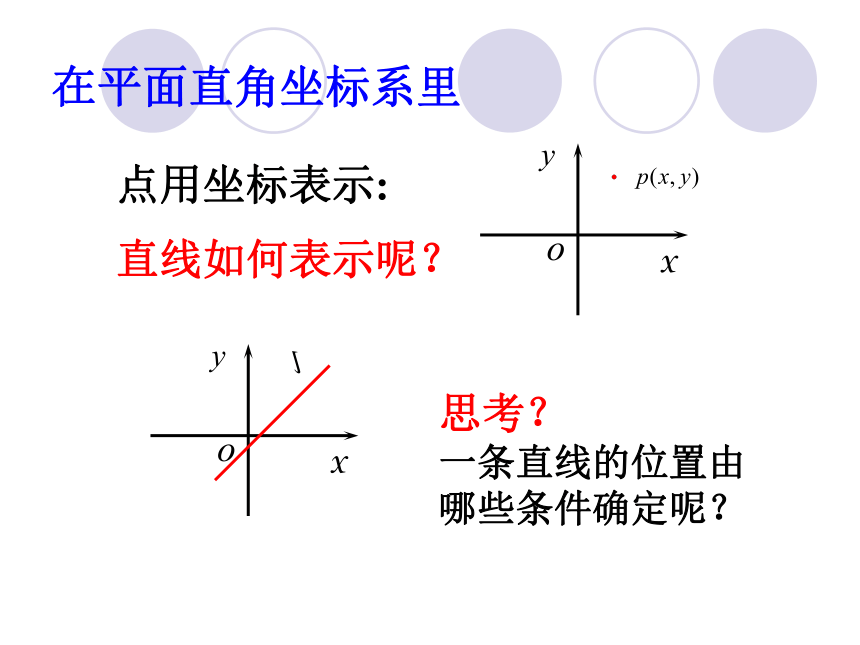
课件27张PPT。3.1直线的倾斜角与斜率在平面直角坐标系里 点用坐标表示:思考?
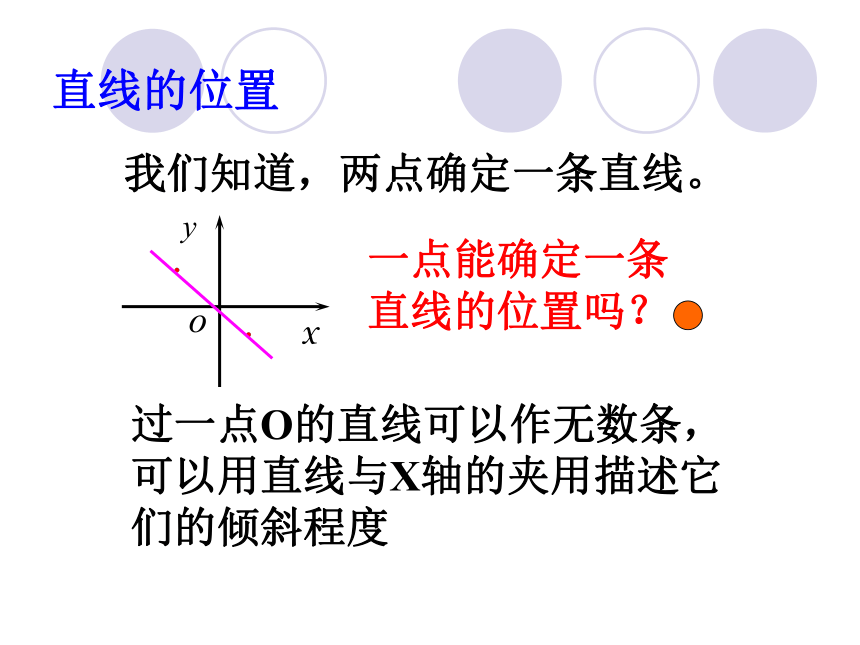
一条直线的位置由哪些条件确定呢? 直线如何表示呢?直线的位置 我们知道,两点确定一条直线。 过一点O的直线可以作无数条,可以用直线与X轴的夹用描述它们的倾斜程度一点能确定一条直线的位置吗?一、直线的倾斜角1、直线倾斜角的定义: 当直线L与X轴相交时,我们取X轴作为基准,X轴正向与直线L向上方向之间所成的角叫做直线的倾斜角(angle of inclination) 注意: (1)直线向上方向;
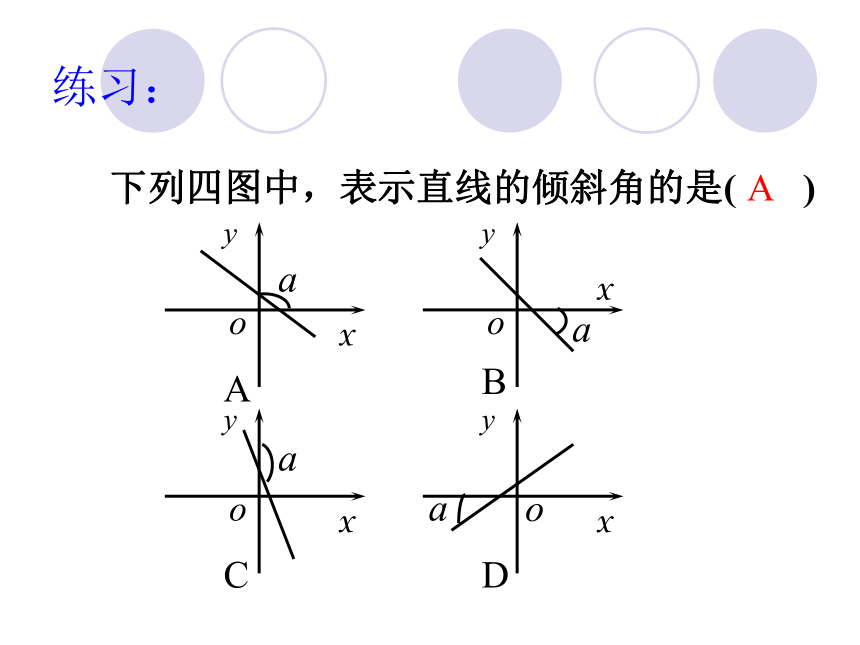
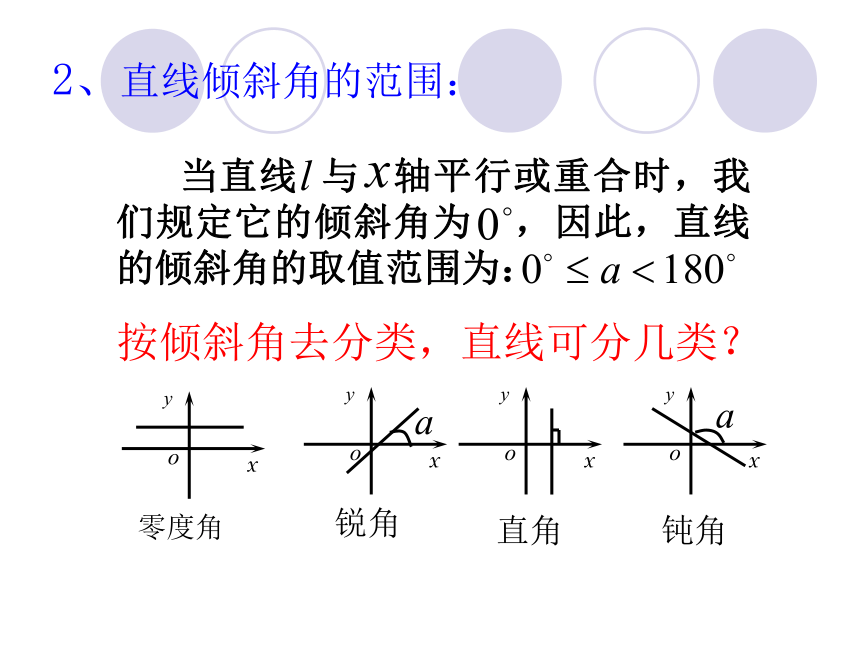
(2)轴的正方向。下列四图中,表示直线的倾斜角的是( )练习: A 2、直线倾斜角的范围: 当直线 与 轴平行或重合时,我们规定它的倾斜角为 ,因此,直线的倾斜角的取值范围为:按倾斜角去分类,直线可分几类? 3、直线倾斜角的意义 体现了直线对轴正方向的倾斜程度
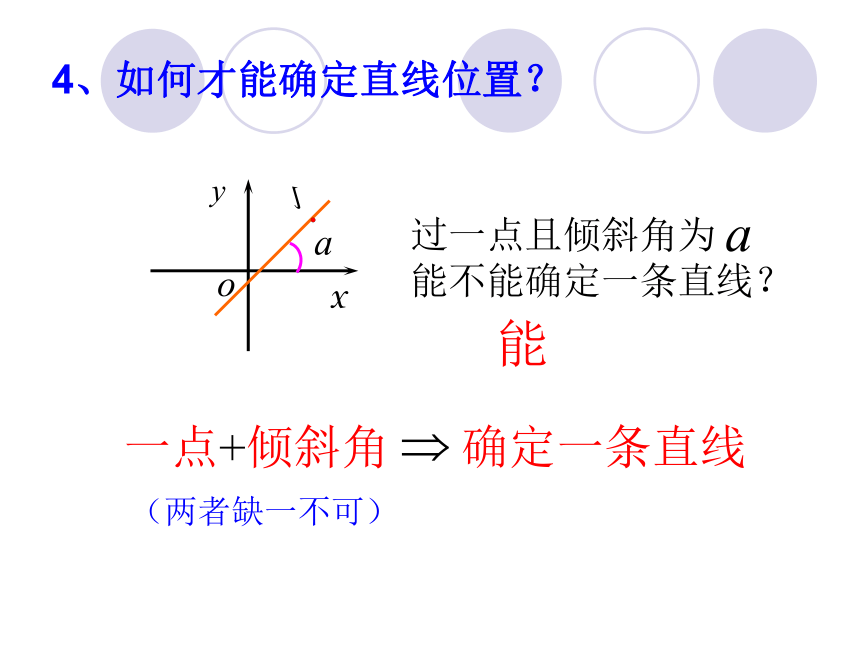
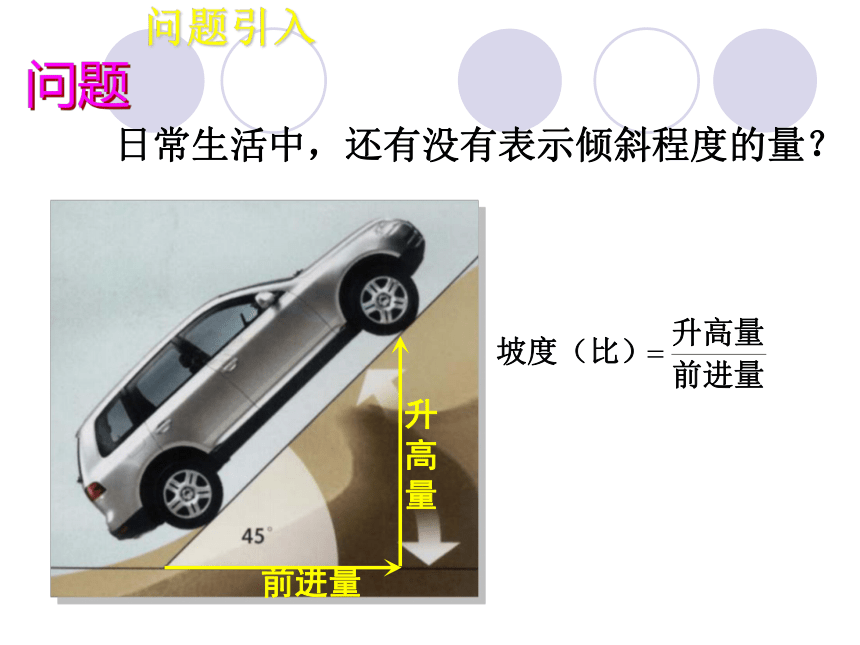
在平面直角坐标系中,每一条直线都有一个确定的倾斜角。 倾斜角相同能确定一条直线吗?相同倾斜角可作无数互相平行的直线4、如何才能确定直线位置?一点+倾斜角 确定一条直线 过一点且倾斜角为 能不能确定一条直线? (两者缺一不可) 能 日常生活中,还有没有表示倾斜程度的量?问题引入问题问题引入问题 例如,“进2升3”与“进3升2”比较,前者更陡一些,因为坡度(比)二、直线的的斜率如图3.1-3,日常生活中,我们经常用“升高量与前进量的比”表示倾斜面的“坡度”(倾斜程度),即设直线的倾斜程度为K 1、直线斜率的定义:我们把一条直线的倾斜角 的正切值叫做这条直线的斜率(slope)。
用小写字母 k 表示,即: 例如: 当α是锐角时,3、探究:由两点确定的直线的斜率如图,当α为锐角时,
能不能构造一个直角三角形去求?锐角 如图,当α为钝角是, 钝角 思考?1、当 的位置对调时, 值又如何呢? 请同学们课后推导!思考?2、当直线平行于x轴,或与x轴重合时,上述公式还适用吗?为什么?答:成立,因为分子为0,分母不为0,K=0 4、直线的斜率公式:1、当直线平行于y轴,或与y轴重合时,上述公式还适用吗?为什么?思考?答:不成立,因为分母为0。2、已知直线上两点 运用上述公式计算直线AB的斜率时,与A、B的顺序有关吗?答:与A、B两点的顺序无关。 例1 如图 ,已知 ,求直线AB,BC,CA的斜率,并判断这些直线的倾斜角是锐角还是钝角.解:直线AB的斜率直线BC的斜率直线CA的斜率 由 及 知,直线AB 与CA的倾斜角均为锐角;由 知,直线BC的倾斜角为钝角.典型例题 例2 在平面直角坐标系中,画出经过原点且斜率分别为1,-1,2及-3的直线 及 .即 解:取 上某一点为 的坐标是 ,根据斜率公式有: 设 ,则 ,于是 的坐标是 .过原点及 的直线即为 .xy 是过原点及 的直线, 是过原点及
的直线, 是过原点及 的直线.典型例题四、练习: 1、解:
(1) ;(2)
(3)
(4)书本P86页 1、2、3 题2、解:(1) ,因为 ,所以
直线CD的倾斜角是锐角;
,因为 ,所以直线
PQ的倾斜角是钝角。 3、解:(1)因为 ,所以 ,
因此,直线AB的倾斜角是 ;
(2)因为过C,D两点的直线垂直x轴,所以
直线CD的倾斜角是 ;
(3)因为 ,所以 ,因此,
直线PQ的倾斜角是 。三、小结: 1、直线的倾斜角定义及其范围:2、直线的斜率定义:3、斜率k与倾斜角 之间的关系:4、斜率公式:
一条直线的位置由哪些条件确定呢? 直线如何表示呢?直线的位置 我们知道,两点确定一条直线。 过一点O的直线可以作无数条,可以用直线与X轴的夹用描述它们的倾斜程度一点能确定一条直线的位置吗?一、直线的倾斜角1、直线倾斜角的定义: 当直线L与X轴相交时,我们取X轴作为基准,X轴正向与直线L向上方向之间所成的角叫做直线的倾斜角(angle of inclination) 注意: (1)直线向上方向;
(2)轴的正方向。下列四图中,表示直线的倾斜角的是( )练习: A 2、直线倾斜角的范围: 当直线 与 轴平行或重合时,我们规定它的倾斜角为 ,因此,直线的倾斜角的取值范围为:按倾斜角去分类,直线可分几类? 3、直线倾斜角的意义 体现了直线对轴正方向的倾斜程度
在平面直角坐标系中,每一条直线都有一个确定的倾斜角。 倾斜角相同能确定一条直线吗?相同倾斜角可作无数互相平行的直线4、如何才能确定直线位置?一点+倾斜角 确定一条直线 过一点且倾斜角为 能不能确定一条直线? (两者缺一不可) 能 日常生活中,还有没有表示倾斜程度的量?问题引入问题问题引入问题 例如,“进2升3”与“进3升2”比较,前者更陡一些,因为坡度(比)二、直线的的斜率如图3.1-3,日常生活中,我们经常用“升高量与前进量的比”表示倾斜面的“坡度”(倾斜程度),即设直线的倾斜程度为K 1、直线斜率的定义:我们把一条直线的倾斜角 的正切值叫做这条直线的斜率(slope)。
用小写字母 k 表示,即: 例如: 当α是锐角时,3、探究:由两点确定的直线的斜率如图,当α为锐角时,
能不能构造一个直角三角形去求?锐角 如图,当α为钝角是, 钝角 思考?1、当 的位置对调时, 值又如何呢? 请同学们课后推导!思考?2、当直线平行于x轴,或与x轴重合时,上述公式还适用吗?为什么?答:成立,因为分子为0,分母不为0,K=0 4、直线的斜率公式:1、当直线平行于y轴,或与y轴重合时,上述公式还适用吗?为什么?思考?答:不成立,因为分母为0。2、已知直线上两点 运用上述公式计算直线AB的斜率时,与A、B的顺序有关吗?答:与A、B两点的顺序无关。 例1 如图 ,已知 ,求直线AB,BC,CA的斜率,并判断这些直线的倾斜角是锐角还是钝角.解:直线AB的斜率直线BC的斜率直线CA的斜率 由 及 知,直线AB 与CA的倾斜角均为锐角;由 知,直线BC的倾斜角为钝角.典型例题 例2 在平面直角坐标系中,画出经过原点且斜率分别为1,-1,2及-3的直线 及 .即 解:取 上某一点为 的坐标是 ,根据斜率公式有: 设 ,则 ,于是 的坐标是 .过原点及 的直线即为 .xy 是过原点及 的直线, 是过原点及
的直线, 是过原点及 的直线.典型例题四、练习: 1、解:
(1) ;(2)
(3)
(4)书本P86页 1、2、3 题2、解:(1) ,因为 ,所以
直线CD的倾斜角是锐角;
,因为 ,所以直线
PQ的倾斜角是钝角。 3、解:(1)因为 ,所以 ,
因此,直线AB的倾斜角是 ;
(2)因为过C,D两点的直线垂直x轴,所以
直线CD的倾斜角是 ;
(3)因为 ,所以 ,因此,
直线PQ的倾斜角是 。三、小结: 1、直线的倾斜角定义及其范围:2、直线的斜率定义:3、斜率k与倾斜角 之间的关系:4、斜率公式:
