2016-2017学年北师大版高中数学必修一课件-2.1 生活中的变量关系 (共12张PPT)
文档属性
| 名称 | 2016-2017学年北师大版高中数学必修一课件-2.1 生活中的变量关系 (共12张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 468.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-11-04 10:30:29 | ||
图片预览




文档简介
课件12张PPT。§1 生活中的变量关系 在我们生活中,变量与变量之间存在依赖关系的实例有哪些? 初中学习过的函数描述了两个变量:
因变量y与自变量x之间有什么样的依赖关系? 因变量y随自变量x的变化而变化:即一个x的取值有唯一确定的值y与之对应,则称y是x的函数.问题情境问题提出 阅读课文23-24页,在高速公路情境下的函数问题:
(1)课本高速公路情境下研究了哪些函数关系?请指出它们的自变量和因变量.
(2)对问题3,储油量v对油面高度h、油面宽度w都存在依赖关系,两种依赖关系都有函数关系吗?
(3)请以高速公路为背景再研究一些函数关系,并思考自变量与因变量交换后是否为函数关系.
(4) 归纳依赖关系与函数关系的区别与联系. 依赖关系与函数关系的区别和联系:
(1)依赖关系不一定是函数关系,但函数关系一定是依赖关系;
(2)若两个变量间存在依赖关系,且对于其中一个变量的每一个值都有另一个变量的唯一值和它对应,则两个变量之间有函数关系;
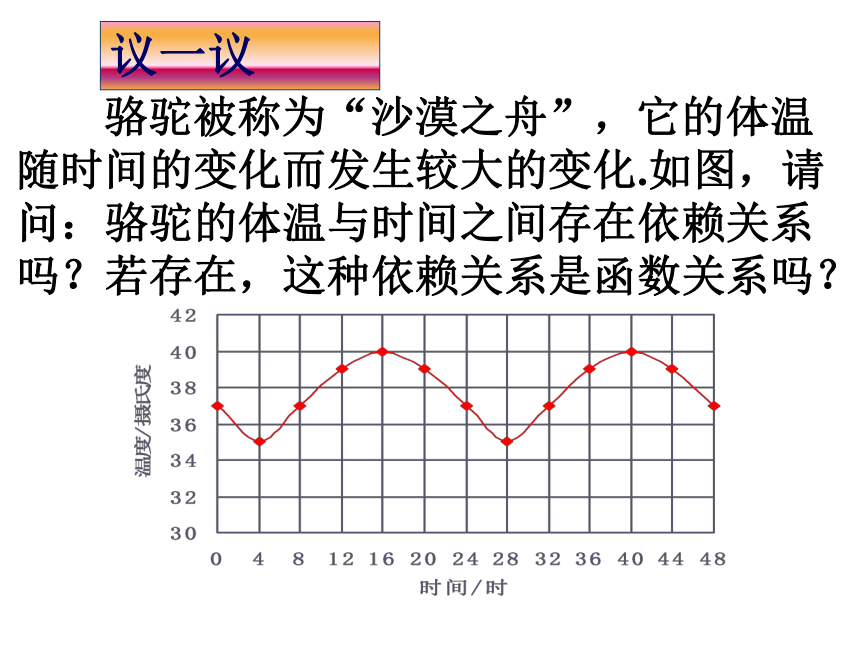
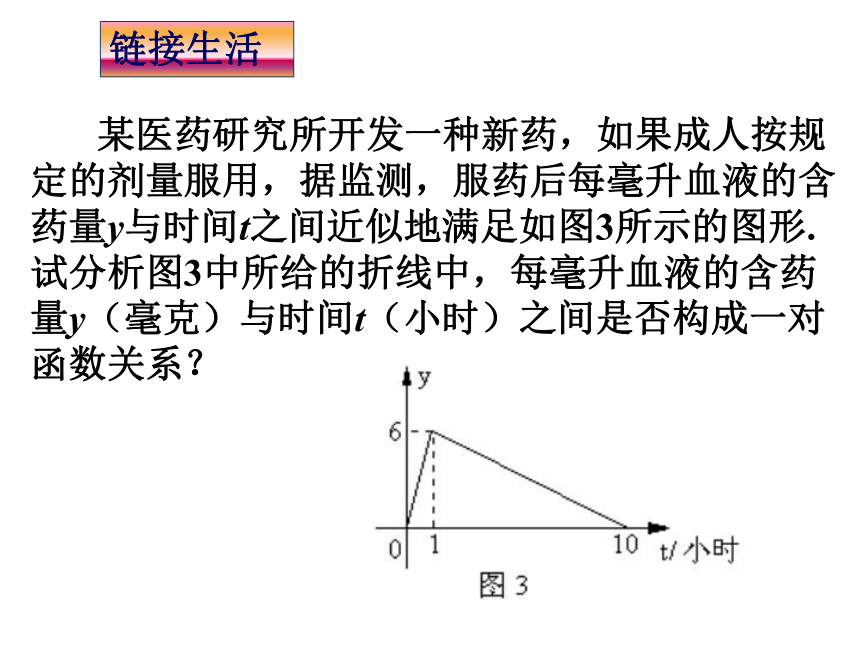
(3)研究函数关系时,通常要指明自变量和因变量,因为两者交换位置后不一定还存在函数关系.探究结论议一议 骆驼被称为“沙漠之舟”,它的体温随时间的变化而发生较大的变化.如图,请问:骆驼的体温与时间之间存在依赖关系吗?若存在,这种依赖关系是函数关系吗?链接生活 某医药研究所开发一种新药,如果成人按规定的剂量服用,据监测,服药后每毫升血液的含药量y与时间t之间近似地满足如图3所示的图形.试分析图3中所给的折线中,每毫升血液的含药量y(毫克)与时间t(小时)之间是否构成一对函数关系? 链接生活 解:由图3知0≤t≤10,每毫升血液中含药量的变化范围为 0≤y≤6,对于0至10中的每一个时间t,在0至6中都有唯一确定的y值与之对应,因此每毫升血液中的含药量y(毫克)与时间t(小时)构成函数关系. 学以致用 一辆汽车在某段路程中的行驶速度与时间的关系如图所示. (1) 试求图中阴影部分的面积,说明面积的实际含义,并分析面积与时间是否形成一对函数关系?
(2)假设汽车里程表在行驶这段路程前的读数为akm, 当1<t≤2时,试建立汽车 里程表的读数s(km)与时间 t(h)的函数关系式. 学以致用 解:(1)阴影部分的面积为
S=50+80+90+70+60=350
阴影部分的面积表示汽车在这5个小时内行驶的总路程为350 km.
(2)根据图有S=80(t-1)+a+50. 1.某电器商店以2 000元一台的价格进了一批电视机,然后以2 100元一台的价格售出,随着售出台数的变化,商店获得的收入是怎样变化的?其收入和售出的台数之间存在函数关系吗?
2.在一定量的水中加入蔗糖,在未到达饱和之前糖水的质量浓度与所加蔗糖的质量之间存在怎样的依赖关系?如果是函数关系,指出自变量和因变量. 课外练习函数关系和依赖关系.
从一般到特殊的数学思想和数形结合的数学思想.
广泛联想能力和热爱数学的态度.归纳小结习题2-1A组1课后作业
因变量y与自变量x之间有什么样的依赖关系? 因变量y随自变量x的变化而变化:即一个x的取值有唯一确定的值y与之对应,则称y是x的函数.问题情境问题提出 阅读课文23-24页,在高速公路情境下的函数问题:
(1)课本高速公路情境下研究了哪些函数关系?请指出它们的自变量和因变量.
(2)对问题3,储油量v对油面高度h、油面宽度w都存在依赖关系,两种依赖关系都有函数关系吗?
(3)请以高速公路为背景再研究一些函数关系,并思考自变量与因变量交换后是否为函数关系.
(4) 归纳依赖关系与函数关系的区别与联系. 依赖关系与函数关系的区别和联系:
(1)依赖关系不一定是函数关系,但函数关系一定是依赖关系;
(2)若两个变量间存在依赖关系,且对于其中一个变量的每一个值都有另一个变量的唯一值和它对应,则两个变量之间有函数关系;
(3)研究函数关系时,通常要指明自变量和因变量,因为两者交换位置后不一定还存在函数关系.探究结论议一议 骆驼被称为“沙漠之舟”,它的体温随时间的变化而发生较大的变化.如图,请问:骆驼的体温与时间之间存在依赖关系吗?若存在,这种依赖关系是函数关系吗?链接生活 某医药研究所开发一种新药,如果成人按规定的剂量服用,据监测,服药后每毫升血液的含药量y与时间t之间近似地满足如图3所示的图形.试分析图3中所给的折线中,每毫升血液的含药量y(毫克)与时间t(小时)之间是否构成一对函数关系? 链接生活 解:由图3知0≤t≤10,每毫升血液中含药量的变化范围为 0≤y≤6,对于0至10中的每一个时间t,在0至6中都有唯一确定的y值与之对应,因此每毫升血液中的含药量y(毫克)与时间t(小时)构成函数关系. 学以致用 一辆汽车在某段路程中的行驶速度与时间的关系如图所示. (1) 试求图中阴影部分的面积,说明面积的实际含义,并分析面积与时间是否形成一对函数关系?
(2)假设汽车里程表在行驶这段路程前的读数为akm, 当1<t≤2时,试建立汽车 里程表的读数s(km)与时间 t(h)的函数关系式. 学以致用 解:(1)阴影部分的面积为
S=50+80+90+70+60=350
阴影部分的面积表示汽车在这5个小时内行驶的总路程为350 km.
(2)根据图有S=80(t-1)+a+50. 1.某电器商店以2 000元一台的价格进了一批电视机,然后以2 100元一台的价格售出,随着售出台数的变化,商店获得的收入是怎样变化的?其收入和售出的台数之间存在函数关系吗?
2.在一定量的水中加入蔗糖,在未到达饱和之前糖水的质量浓度与所加蔗糖的质量之间存在怎样的依赖关系?如果是函数关系,指出自变量和因变量. 课外练习函数关系和依赖关系.
从一般到特殊的数学思想和数形结合的数学思想.
广泛联想能力和热爱数学的态度.归纳小结习题2-1A组1课后作业
