2016-2017学年北师大版高中数学必修一课件-3.5.3 对数函数的图像与性质 (共15张PPT)
文档属性
| 名称 | 2016-2017学年北师大版高中数学必修一课件-3.5.3 对数函数的图像与性质 (共15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 525.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-11-04 10:51:33 | ||
图片预览





文档简介
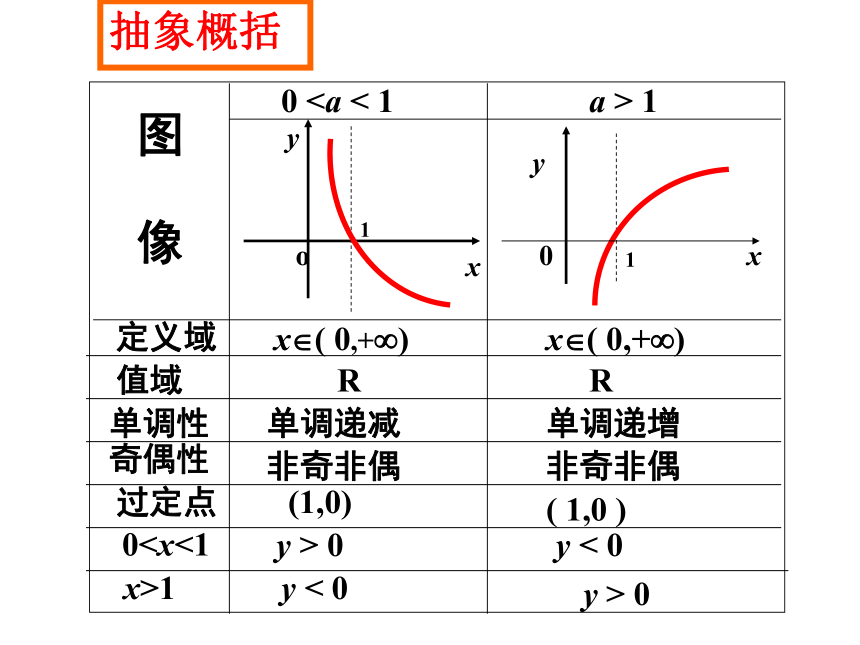
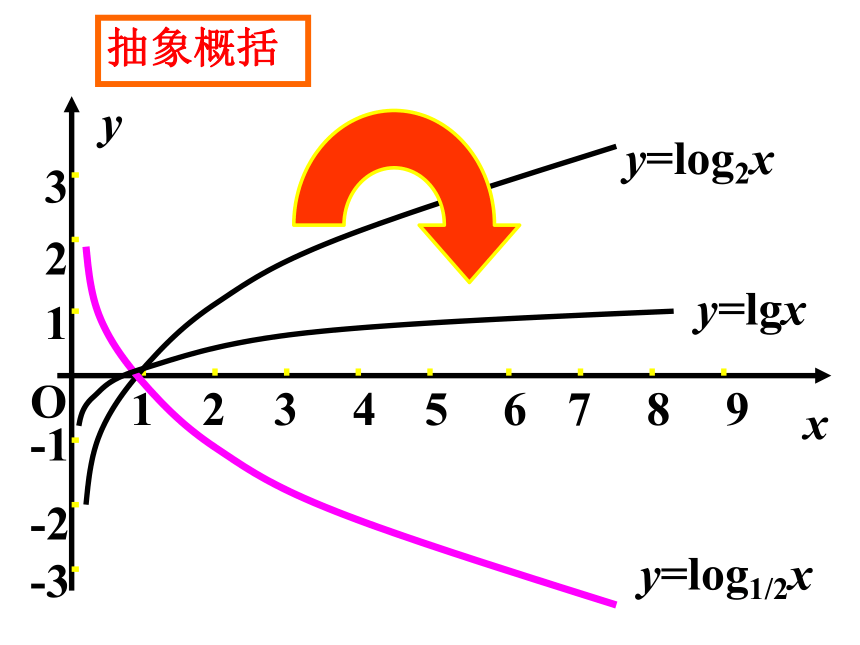
课件15张PPT。5.3 对数函数的图像与性质定义域x?( 0,+?)值域 R R单调性奇偶性过定点01单调递减单调递增非奇非偶非奇非偶(1,0)( 1,0 ) y > 0 y < 0y < 0y > 0图 像0 1x?( 0,+?)抽象概括Oxy123456789123-1-2-3y=log2xy=lgxy=log1/2x抽象概括(1)随着底数a的增大,图像在同一象限内的位置按顺时针转.(2)y=logax与y=log1/ax的图像关于x轴对称.(3)对数函数是非奇非偶函数.抽象概括例1求下列函数的定义域:(1) y=logax2; (2) y=loga(4-x);解:(1)因为x2>0,所以x≠?,即函数y=logax2的定义域为 ?-???? ? (0,+??. (2)因为 4-x>0,所以x<4,即函数y=loga(4-x)的定义域为(-??4). (3) y=log(x-1)(3-x); (4) y=?log0.5(4x-3).例题解析(3) 因为 3-x>0,
x-1>0,
x-1≠?,所以 10,
log0.5(4x-3)?0,x>3/4
4x-3≤?定义域为(3/4,1].例题解析例 2比较下列各组中两个值的大小:(1) log23 , log23.5 (2) log0.71.6 , logo.71.8 解:(1)考察对数函数y=log2x,因为 2>1, 3<3.5所以log23log0.71.8.例题解析求下列函数的定义域、值域:解:要使函数有意义,必须:即:值域:因为所以从而,故所以,即例 3 例题解析解:因为 所以函数定义域为R,对一切实数都恒有从而即函数值域为从而定义域为[-1,1],值域为例题解析.,,,.解:函数有意义,必须:由即值域为,所以在此区间内 所以从而例题解析
.解:要使函数有意义,必须: 由(1)由(2)当时必须 当时必须 综合(1)(2)得 例题解析,,,.,所以 当时所以例题解析原函数定义域为: 所以比较两个对数式的大小,一般有三种方法:(1)若是同底的对数,则可直接利用对数函数的单调性,只需比较两个真数的大小即可.(2)若是不同底的对数式,方法有:10“搭桥法”,20同底化法30图像法(3)比较法,包括作差法和作商法.归纳总结比较log56和log47的大小关系解: 利用对数函数图像.由函数单调性 log56log47.得到 log57
x-1>0,
x-1≠?,所以 1
log0.5(4x-3)?0,x>3/4
4x-3≤?定义域为(3/4,1].例题解析例 2比较下列各组中两个值的大小:(1) log23 , log23.5 (2) log0.71.6 , logo.71.8 解:(1)考察对数函数y=log2x,因为 2>1, 3<3.5所以log23
.解:要使函数有意义,必须: 由(1)由(2)当时必须 当时必须 综合(1)(2)得 例题解析,,,.,所以 当时所以例题解析原函数定义域为: 所以比较两个对数式的大小,一般有三种方法:(1)若是同底的对数,则可直接利用对数函数的单调性,只需比较两个真数的大小即可.(2)若是不同底的对数式,方法有:10“搭桥法”,20同底化法30图像法(3)比较法,包括作差法和作商法.归纳总结比较log56和log47的大小关系解: 利用对数函数图像.由函数单调性 log56
