2016-2017学年北师大版高中数学必修一课件-4.1.1利用函数性质判定方程解的存在 (共12张PPT)
文档属性
| 名称 | 2016-2017学年北师大版高中数学必修一课件-4.1.1利用函数性质判定方程解的存在 (共12张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 695.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-11-04 10:53:07 | ||
图片预览




文档简介
课件12张PPT。1.1 利用函数性质判定
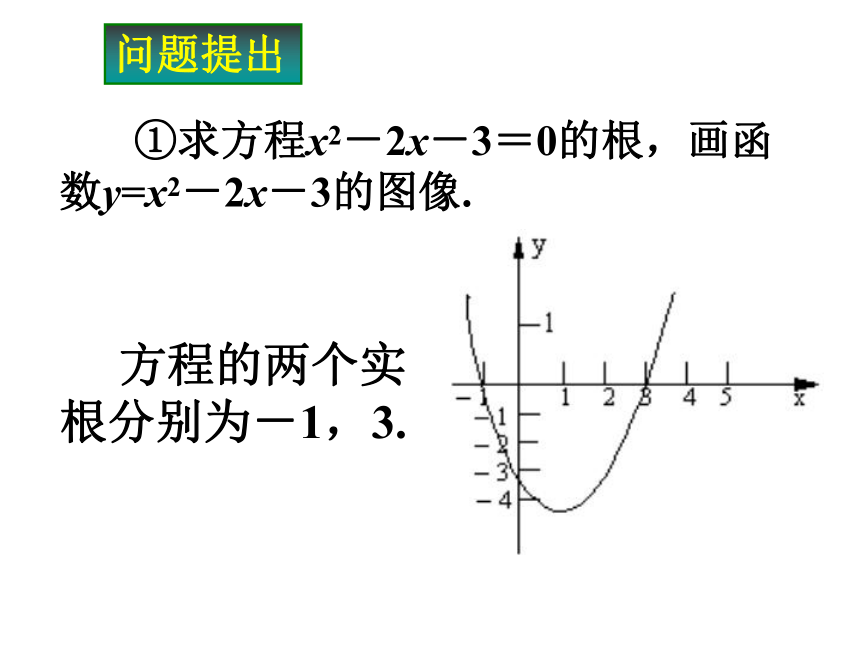
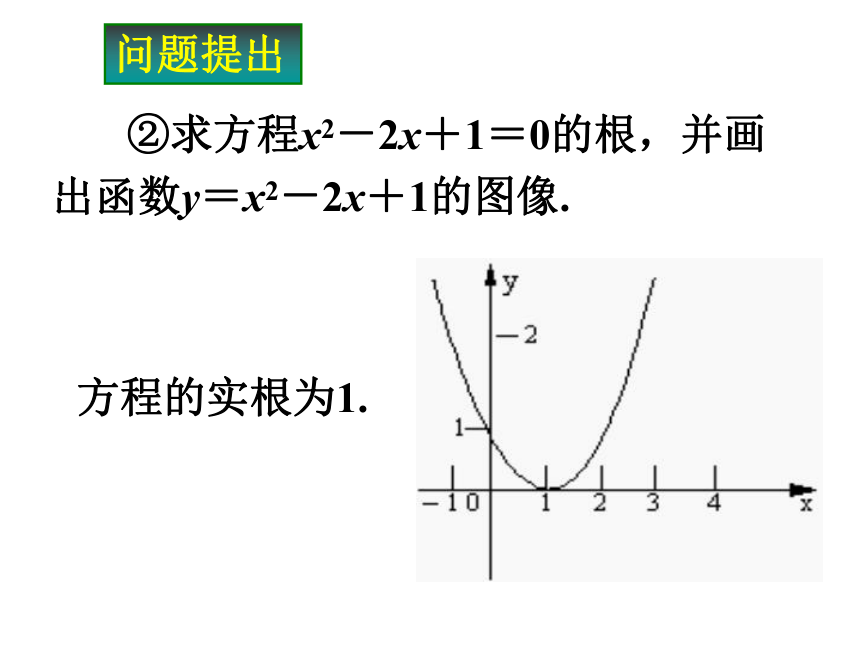
方程解的存在1问题提出1 ①求方程x2-2x-3=0的根,画函数y=x2-2x-3的图像. 方程的两个实根分别为-1,3.问题提出1 ②求方程x2-2x+1=0的根,并画出函数y=x2-2x+1的图像. 方程的实根为1.议一议1 1.观察图像:方程的根与函数的图像和x轴的交点的横坐标有什么关系? 方程的根就是函数的图像与x轴交点的横坐标.2.归纳函数零点的概念 一般对于函数y=f(x),我们把f(x)=0的实数x叫作函数y=f(x)的零点.议一议1 3.如何判断一元二次方程根的个数,如何判断二次函数图像与x轴交点的个数,它们之间有什么关系? 一元二次方程根的个数就是二次函数图像与x轴交点的个数,可以用判别式法来制定一元二次方程根的个数,当△>0时,有两个不相等的实根x1、x2,相应的二次函数的图像与x轴的两个交点(x1,0)、(x2,0);当△=0时,一元二次方程有两个相等的实根x1=x2,相应的二次函数的图像与x轴有唯一的交点(x,0);当△<0时,一元二次方程没有实根,相应的二次方程与x轴没有交点.议一议15.函数的图像不易画出时,又不能求相应方程的根时,怎样判断函数是否有零点?4.怎样判断函数是否有零点?(按思维顺序给出)方程f(x)=0有实根→函数y=f(x)的图像与x轴有交点→函数y=f(x)有零点.议一议1 观察二次函数f(x)=x2-2x-3的图像,可知f(x)= x2 -2x-3在区间[-2,1] 上有零点,计算f(-2)与f(1)的乘积,这个乘积的特点小于零,在区间[2,4] 同样如此f(-2)·f(1)<0,函数y= x2 -2x-3在区间(-2,1)内有零点x=-1,它是方程x2 -2x-3=0的一个根,同样地,f(2)·f(4)<0,函数y= x2 -2x-3在(2,4)内有零点x=3,它是方程x2 -2x-3=0的另一根.归纳小结1 若函数y=f(x)在闭区间[a, b] 上的图像是连续的曲线,并且在区间端点的函数值符号相反,即f(a)·f(b)<0,则在区间(a, b)内,函数y=f(x)至少有一个零点,即相应的方程f(x)=0在区间(a, b)内至少有一个实数解.例题解析1 例1 已知函数f(x)=3x-x2+1,问:方程f(x)=0在区间[-1,0] 内有没有实数解?为什么?解:因为 f(-1)= - 3-(-1)2+1=-3<0,f(0)=3·0-(0)2+1=1>0,f(-1)·f(0)<0,又f(x)=3x-x2+1的图像是连续曲线,所以f(x)在区间[-1, 0]内有零点,即f(x)=0在区间[-1, 0] 内有实数解.例题解析1 例 2 判定方程(x-2)(x-5)=1有两个相异的实数解,且一个大于5,一个小于2. 分析:转化判断函数
f(x)=(x-2) (x-5)-1,在(-∞,2)和(5,+∞)内各有一个零点.例题解析1故方程(x-2) (x-5)=1有两个相异的实数解,且一个大于4,一个小于2.解:设函数f(x)=(x-2) (x-5)-1,有f(5)=(5-2) (5-5)-1=1,
f(2) =(2-2) (2-5)-1=-1,因为f(x)为开口向上的抛物线,所以抛物线与横轴在(5,+∞),(-∞,2)内各有一个交点.课后作业
课本P116 练习1
f(x)=(x-2) (x-5)-1,在(-∞,2)和(5,+∞)内各有一个零点.例题解析1故方程(x-2) (x-5)=1有两个相异的实数解,且一个大于4,一个小于2.解:设函数f(x)=(x-2) (x-5)-1,有f(5)=(5-2) (5-5)-1=1,
f(2) =(2-2) (2-5)-1=-1,因为f(x)为开口向上的抛物线,所以抛物线与横轴在(5,+∞),(-∞,2)内各有一个交点.课后作业
课本P116 练习1
