高二数学诊断性试卷
图片预览


文档简介
高二数学诊断性试卷
第Ⅰ卷 选择题(共50分)
一、选择题:(本大题共10小题,每小题5分,共50分,在每小题中只有一项符合题意的。)
1.下列表述正确的是( )www.ks5u.com
①归纳推理是由部分到整体的推理;②归纳推理是由一般到一般的推理;③演绎推理是由一般到特殊的推理;④类比推理是由特殊到一般的推理;⑤类比推理是由特殊到特殊的推理www.ks5u.com
A. ①②③ B. ②③④ C. ②④⑤ D. ①③⑤
2、曲线y=x3-3x2+1在点(1,-1)处的切线方程为( )www.ks5u.com
A. y=3x-4 B. y=-3x+2 C. y=-4x+3 D. y=4x-5
3、函数y=x3-3x2-9x(-2<x<2)有( )www.ks5u.com
A. 极大值5,极小值-27 B. 极大值5,极小值-11
C. 极大值5,无极小值 D. 极小值-27,无极大值
4、y=esinxcos(sinx),则yˊ(0)等于( )www.ks5u.com
A. 0 B. 1 C. -1 D. 2
5、已知n为正偶数,用数学归纳法证明( )www.ks5u.com
1-时,若已假设n=k(k≥2且k为偶数)时命题为真,则还需要用归纳假设再证( )www.ks5u.com
A. n=k+1时等式成立 B. n=k+2时等式成立
C. n=2k+2时等式成立 D. n=2(k+2)时等式成立
6、数列中,a1=1, 表示前n项和,且,,2成等差数列,通过计算s1,s2,s3,猜想当n≥1时,= ( )
A. B. C. D.
7、已知实数a,b,c满足a+b+c=0,abc>0,则的值.( ) www.ks5u.com
A. 一定是正数 B. 一定是负数 C. 可能为0 D. 正、负不能确定
8、定义运算:□:a□b=a(1-b),若不等式(x-a)□(x+a)≥1对任何实数x都不成立,则实数a的取值范围是 ( )www.ks5u.com
A. -1<a<1 B. 0<a<2 C. <a< D. <a<
9、设a>b>0,x=,y=,则x、y的大小关系为( )
A. x>y B. x<y C. x=y D. x、y大小关系不定
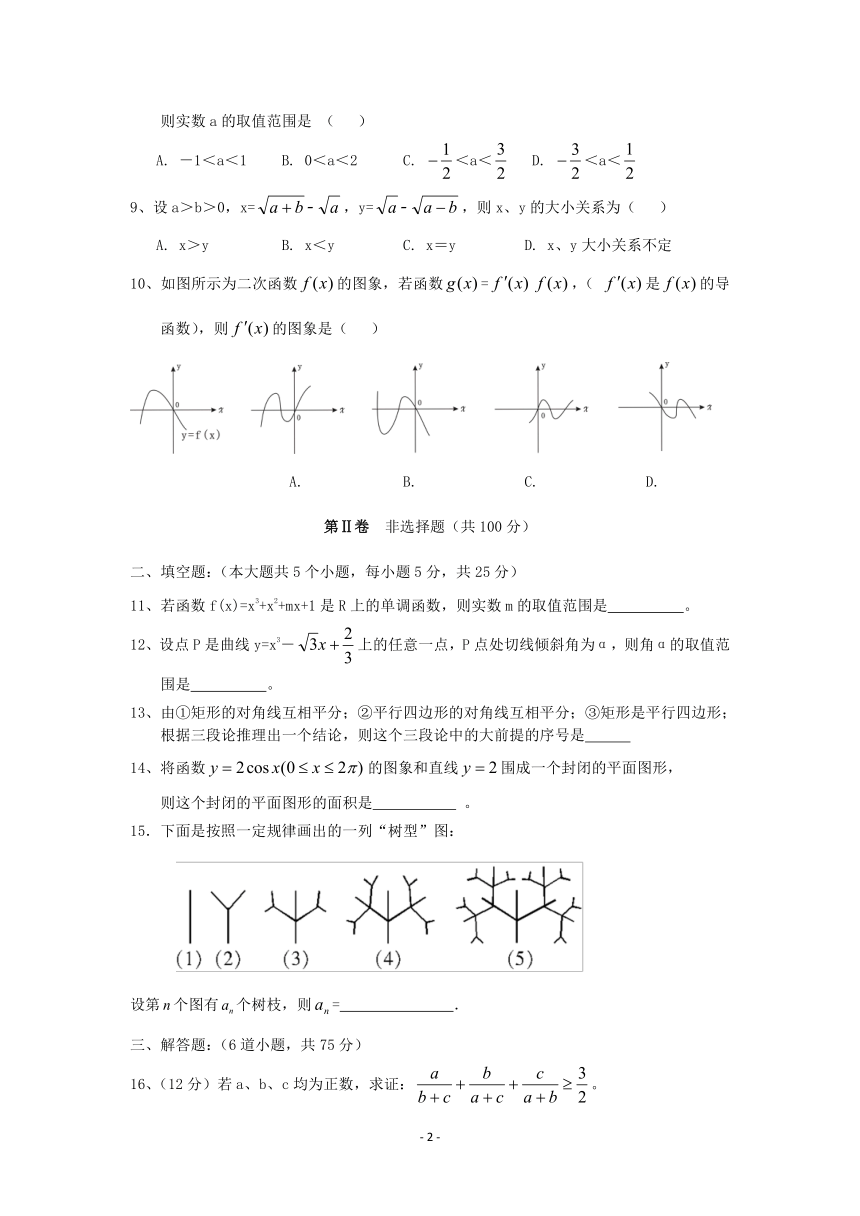
10、如图所示为二次函数的图象,若函数=,( 是的导函数),则的图象是( )www.ks5u.com
A. B. C. D.
第Ⅱ卷 非选择题(共100分)
二、填空题:(本大题共5个小题,每小题5分,共25分)www.ks5u.com
11、若函数f(x)=x3+x2+mx+1是R上的单调函数,则实数m的取值范围是 。
12、设点P是曲线y=x3-上的任意一点,P点处切线倾斜角为α,则角α的取值范围是 。www.ks5u.com
13、由①矩形的对角线互相平分;②平行四边形的对角线互相平分;③矩形是平行四边形;根据三段论推理出一个结论,则这个三段论中的大前提的序号是
14、将函数的图象和直线围成一个封闭的平面图形,
则这个封闭的平面图形的面积是 。
15.下面是按照一定规律画出的一列“树型”图:
设第个图有个树枝,则= .
三、解答题:(6道小题,共75分)www.ks5u.com
16、(12分)若a、b、c均为正数,求证:。
17、(12分)设函数.
(I)证明:是函数在区间上递增的充分而不必要的条件;
(II)若时,满足恒成立,求实数的取值范围.
18、(12分)已知函数f(x)=ax3-bx2 +(2-b)x+1,在处取得极大值,在处取得极小值,且0<x1<1<x2<2。
(1)证明:a>0;www.ks5u.com
(2)若z=a+2b,求z的取值范围。W
ww.ks5u.com
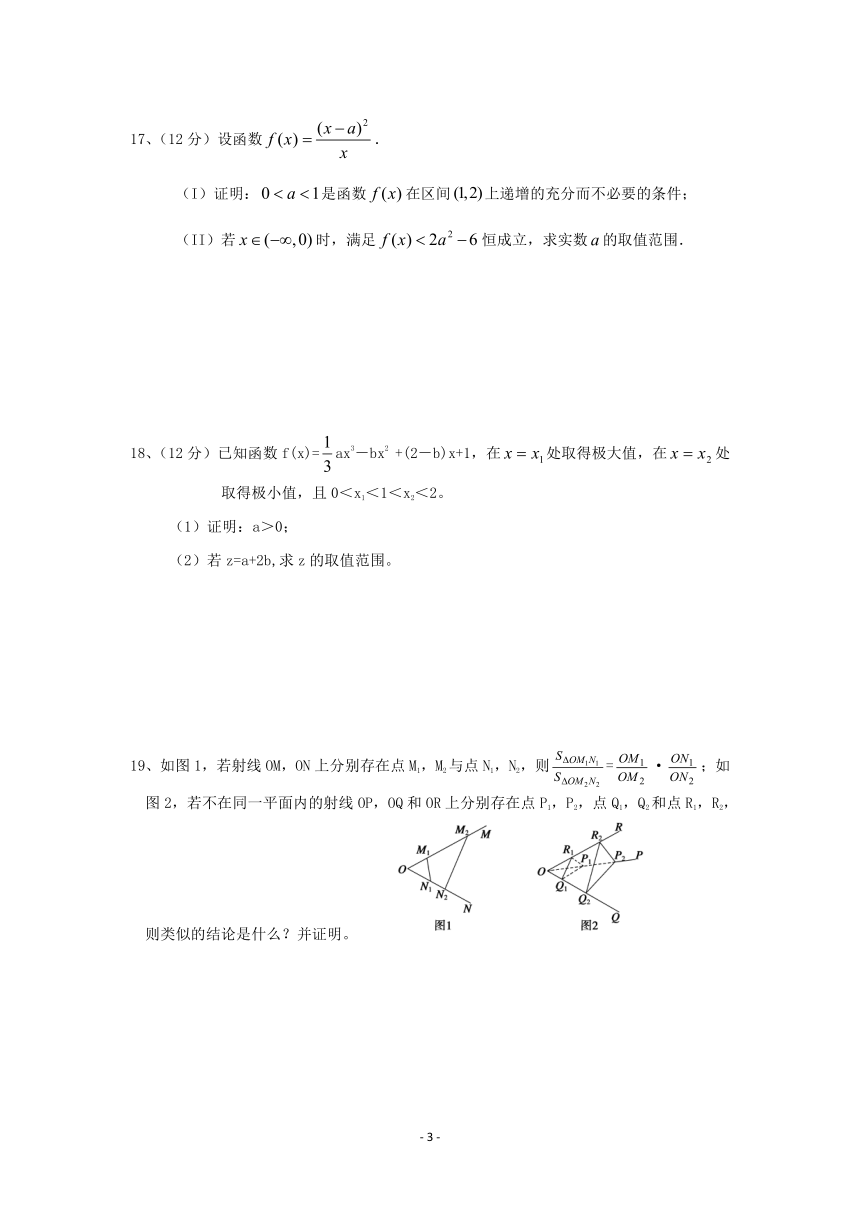
19、如图1,若射线OM,ON上分别存在点M1,M2与点N1,N2,则=·;如图2,若不在同一平面内的射线OP,OQ和OR上分别存在点P1,P2,点Q1,Q2和点R1,R2,则类似的结论是什么?并证明。
20、(13分)如图,有一块半椭圆形钢板,其长半轴长为2r,短半轴长为r,计划将此钢板割成等腰梯形的形状,下底AB是半椭圆的短轴,上底CD的端点在椭圆上,记CD=2x,梯形面积为S。www.ks5u.com
(1)求面积S以x为自变量的函数式,并写出其定义域;
(2)求面积S的最大值。
21、 (本题满分14分)已知= ,数列满足:
,
(1)求在上的最大值和最小值;
(2)证明:;
(3)判断与的大小,并说明理由.
答案
一、选择题
题号
1
2
3
4
5
6
7
8
9
10
答案
D
B
C
B
B
B
B
C
B
A
二、填空题
11、[,+∞); 12、[0,﹚[,);
13、② ;www.ks5u.c14、 15、()
三、解答题
16、证明:欲证,
只要证,
只要证,
只要证(a+b+c)()≥。
∵(a+b+c)()www.ks5u.com
=[(b+c)+(a+c)+(a+b)]·()
≥×3·3=,故原不等式成立。
17、解(I)对函数求导,得 ,
先证充分性:若,,,
函数在区间上递增.
再说明非必要性:在区间上递增, ∴对1由得,,而,所以,即
所以,是函数在区间上递增的充分而不必要的条件。
(II) ,令,得
显然,时不符合题意.
当时,函数在()上递增,在上递减,
若时,恒成立,需=6
,得.
当时,函数在()上递增,在上递减,
此时,,如满足恒成立,
需得
故若时,满足恒成立,实数
18、解:求函数f′(x)的导数f′(x)=ax2-2bx+2-b
(1)由函数f(x)在x=x1处取得极大值,在x=x2处取得极小值,知x1,x2是f’(x)=0的两个根。www.ks5u.com
所以f’(x)=a(x-x1)(x-x2)
当x<x1时,f(x)为增函数,f′(x)>0,由x-x1<0,x-x2<0得a>0
(2)在题设下,0<x1<1<x2<2等价于即
化简得此不等式组表示的区域为平面aob上三条直线:2-b=0,a-3b+2=0,4a-5b+2=0,所围成的ABC的内部,其三个顶点分别为:A. www.ks5u.com
在这三点的值依次为,所以z的取值范围为
19、解 类似的结论为:=··.
这个结论是正确的,证明如下:
如图,过R2作R2M2⊥平面P2OQ2于M2,连OM2.
过R1在平面OR2M2作R1M1∥R2M2交OM2于M1,
则R1M1⊥平面P2OQ2.
由=·R1M1
=·OP1·OQ1·sin∠P1OQ1·R1M1
=OP1·OQ1·R1M1·sin∠P1OQ1,
同理,=OP2·OQ2·R2M2·sin∠P2OQ2.
所以=.
由平面几何知识可得=.
所以=.所以结论正确.
20、解析:(1)依题意,以AB的中点O为原点建立直角坐标系O-xy(如图),则点C的横坐标为x。www.ks5u.com
点C的纵坐标y满足方程+=1(y≥0),解得y=2(0<x<r)
S=·2=2(x+r)·,其定义域为{x|0<x<r}
(2)记f(x)=4(x+r) 2(r2-x2),0<x<r,
则f’(x)=8(x+r)2(r-2x) www.ks5u.com
令f’(x)=0,得x=
因为当0<x<时,f’(x)>0;www.ks5u.com
当<x<r时,f’(x)<0,所以f()是f(x)的最大值
因此,当x=时,S也取得最大值,最大值为=
即梯形面积S的最大值为 www.ks5u.com
21、【解】 (1)
当时,
在上是增函数
………………6分
(2)(数学归纳法证明)
①当时,由已知成立;
②假设当时命题成立,即成立,
那么当时,由①得
,这就是说时命题成立.
由①、②知,命题对于都成立 …………9分
(3) 由
记得 ……10分
当时,故
所以 <0 得g(x)在是减函数,
∴g(x)>g(0)=f(0)-2=0 ∴>0,即>0
得>
第Ⅰ卷 选择题(共50分)
一、选择题:(本大题共10小题,每小题5分,共50分,在每小题中只有一项符合题意的。)
1.下列表述正确的是( )www.ks5u.com
①归纳推理是由部分到整体的推理;②归纳推理是由一般到一般的推理;③演绎推理是由一般到特殊的推理;④类比推理是由特殊到一般的推理;⑤类比推理是由特殊到特殊的推理www.ks5u.com
A. ①②③ B. ②③④ C. ②④⑤ D. ①③⑤
2、曲线y=x3-3x2+1在点(1,-1)处的切线方程为( )www.ks5u.com
A. y=3x-4 B. y=-3x+2 C. y=-4x+3 D. y=4x-5
3、函数y=x3-3x2-9x(-2<x<2)有( )www.ks5u.com
A. 极大值5,极小值-27 B. 极大值5,极小值-11
C. 极大值5,无极小值 D. 极小值-27,无极大值
4、y=esinxcos(sinx),则yˊ(0)等于( )www.ks5u.com
A. 0 B. 1 C. -1 D. 2
5、已知n为正偶数,用数学归纳法证明( )www.ks5u.com
1-时,若已假设n=k(k≥2且k为偶数)时命题为真,则还需要用归纳假设再证( )www.ks5u.com
A. n=k+1时等式成立 B. n=k+2时等式成立
C. n=2k+2时等式成立 D. n=2(k+2)时等式成立
6、数列中,a1=1, 表示前n项和,且,,2成等差数列,通过计算s1,s2,s3,猜想当n≥1时,= ( )
A. B. C. D.
7、已知实数a,b,c满足a+b+c=0,abc>0,则的值.( ) www.ks5u.com
A. 一定是正数 B. 一定是负数 C. 可能为0 D. 正、负不能确定
8、定义运算:□:a□b=a(1-b),若不等式(x-a)□(x+a)≥1对任何实数x都不成立,则实数a的取值范围是 ( )www.ks5u.com
A. -1<a<1 B. 0<a<2 C. <a< D. <a<
9、设a>b>0,x=,y=,则x、y的大小关系为( )
A. x>y B. x<y C. x=y D. x、y大小关系不定
10、如图所示为二次函数的图象,若函数=,( 是的导函数),则的图象是( )www.ks5u.com
A. B. C. D.
第Ⅱ卷 非选择题(共100分)
二、填空题:(本大题共5个小题,每小题5分,共25分)www.ks5u.com
11、若函数f(x)=x3+x2+mx+1是R上的单调函数,则实数m的取值范围是 。
12、设点P是曲线y=x3-上的任意一点,P点处切线倾斜角为α,则角α的取值范围是 。www.ks5u.com
13、由①矩形的对角线互相平分;②平行四边形的对角线互相平分;③矩形是平行四边形;根据三段论推理出一个结论,则这个三段论中的大前提的序号是
14、将函数的图象和直线围成一个封闭的平面图形,
则这个封闭的平面图形的面积是 。
15.下面是按照一定规律画出的一列“树型”图:
设第个图有个树枝,则= .
三、解答题:(6道小题,共75分)www.ks5u.com
16、(12分)若a、b、c均为正数,求证:。
17、(12分)设函数.
(I)证明:是函数在区间上递增的充分而不必要的条件;
(II)若时,满足恒成立,求实数的取值范围.
18、(12分)已知函数f(x)=ax3-bx2 +(2-b)x+1,在处取得极大值,在处取得极小值,且0<x1<1<x2<2。
(1)证明:a>0;www.ks5u.com
(2)若z=a+2b,求z的取值范围。W
ww.ks5u.com
19、如图1,若射线OM,ON上分别存在点M1,M2与点N1,N2,则=·;如图2,若不在同一平面内的射线OP,OQ和OR上分别存在点P1,P2,点Q1,Q2和点R1,R2,则类似的结论是什么?并证明。
20、(13分)如图,有一块半椭圆形钢板,其长半轴长为2r,短半轴长为r,计划将此钢板割成等腰梯形的形状,下底AB是半椭圆的短轴,上底CD的端点在椭圆上,记CD=2x,梯形面积为S。www.ks5u.com
(1)求面积S以x为自变量的函数式,并写出其定义域;
(2)求面积S的最大值。
21、 (本题满分14分)已知= ,数列满足:
,
(1)求在上的最大值和最小值;
(2)证明:;
(3)判断与的大小,并说明理由.
答案
一、选择题
题号
1
2
3
4
5
6
7
8
9
10
答案
D
B
C
B
B
B
B
C
B
A
二、填空题
11、[,+∞); 12、[0,﹚[,);
13、② ;www.ks5u.c14、 15、()
三、解答题
16、证明:欲证,
只要证,
只要证,
只要证(a+b+c)()≥。
∵(a+b+c)()www.ks5u.com
=[(b+c)+(a+c)+(a+b)]·()
≥×3·3=,故原不等式成立。
17、解(I)对函数求导,得 ,
先证充分性:若,,,
函数在区间上递增.
再说明非必要性:在区间上递增, ∴对1
所以,是函数在区间上递增的充分而不必要的条件。
(II) ,令,得
显然,时不符合题意.
当时,函数在()上递增,在上递减,
若时,恒成立,需=6
,得.
当时,函数在()上递增,在上递减,
此时,,如满足恒成立,
需得
故若时,满足恒成立,实数
18、解:求函数f′(x)的导数f′(x)=ax2-2bx+2-b
(1)由函数f(x)在x=x1处取得极大值,在x=x2处取得极小值,知x1,x2是f’(x)=0的两个根。www.ks5u.com
所以f’(x)=a(x-x1)(x-x2)
当x<x1时,f(x)为增函数,f′(x)>0,由x-x1<0,x-x2<0得a>0
(2)在题设下,0<x1<1<x2<2等价于即
化简得此不等式组表示的区域为平面aob上三条直线:2-b=0,a-3b+2=0,4a-5b+2=0,所围成的ABC的内部,其三个顶点分别为:A. www.ks5u.com
在这三点的值依次为,所以z的取值范围为
19、解 类似的结论为:=··.
这个结论是正确的,证明如下:
如图,过R2作R2M2⊥平面P2OQ2于M2,连OM2.
过R1在平面OR2M2作R1M1∥R2M2交OM2于M1,
则R1M1⊥平面P2OQ2.
由=·R1M1
=·OP1·OQ1·sin∠P1OQ1·R1M1
=OP1·OQ1·R1M1·sin∠P1OQ1,
同理,=OP2·OQ2·R2M2·sin∠P2OQ2.
所以=.
由平面几何知识可得=.
所以=.所以结论正确.
20、解析:(1)依题意,以AB的中点O为原点建立直角坐标系O-xy(如图),则点C的横坐标为x。www.ks5u.com
点C的纵坐标y满足方程+=1(y≥0),解得y=2(0<x<r)
S=·2=2(x+r)·,其定义域为{x|0<x<r}
(2)记f(x)=4(x+r) 2(r2-x2),0<x<r,
则f’(x)=8(x+r)2(r-2x) www.ks5u.com
令f’(x)=0,得x=
因为当0<x<时,f’(x)>0;www.ks5u.com
当<x<r时,f’(x)<0,所以f()是f(x)的最大值
因此,当x=时,S也取得最大值,最大值为=
即梯形面积S的最大值为 www.ks5u.com
21、【解】 (1)
当时,
在上是增函数
………………6分
(2)(数学归纳法证明)
①当时,由已知成立;
②假设当时命题成立,即成立,
那么当时,由①得
,这就是说时命题成立.
由①、②知,命题对于都成立 …………9分
(3) 由
记得 ……10分
当时,故
所以 <0 得g(x)在是减函数,
∴g(x)>g(0)=f(0)-2=0 ∴>0,即>0
得>
