湖南省常德市石门一中2015-2016学年高一(下)入学数学试卷(解析版)
文档属性
| 名称 | 湖南省常德市石门一中2015-2016学年高一(下)入学数学试卷(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 186.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-11-04 11:05:37 | ||
图片预览




文档简介
2015-2016学年湖南省常德市石门一中高一(下)入学数学试卷
一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合M={1,2,3},N={2,3,4},则( )
A.M N
B.N M
C.M∩N={2,3}
D.M∪N={2,4}
2.已知函数,那么f[f()]的值为( )
A.9
B.
C.﹣9
D.﹣
3.在直角坐标系中,下列直线中倾斜角为钝角的是( )
A.y=3x﹣1
B.x+2=0
C.
+=1
D.2x﹣y+1=0
4.线段x﹣2y+1=0(﹣1≤x≤3)的垂直平分线方程为( )
A.x+2y﹣3=0
B.2x+y﹣3=0
C.2x+y﹣1=0
D.2x﹣y﹣1=0
5.函数f(x)=x﹣3+log3x的零点所在区间是( )
A.(0,1)
B.(1,2)
C.(2,3)
D.(3,+∞)
6.已知a、b∈R,且满足0<a<1<b,则下列大小关系正确的是( )
A.ab<ba<logab
B.ba<logab<ab
C.logab<ba<ab
D.logab<ab<ba
7.函数f(x)=(1﹣x)|x﹣3|在(﹣∞,a]上取得最小值﹣1,则实数a的取值范围是( )
A.(﹣∞,2]
B.
C.
D.[2,+∞)
8.设奇函数f(x)在(0,+∞)上为增函数,且,则不等式x[f(x)﹣f(﹣x)]<0的解集为( )
A.
B.
C.
D.
9.用半径为R的半圆卷成一个无底圆锥,则这个无底圆锥的体积为( )
A.
B.
C.
D.
10.给出下面四个命题(其中m,n,l是空间中不同的直线,α,β是空间中不同的平面)中错误的命题个数为( )
①m∥n,n∥α m∥α
②α⊥β,α∩β=m,l⊥m l⊥β
③l⊥m,l⊥n,m α,n α l⊥α
④m∩n=A,m∥α,m∥β,n∥α,n∥β α∥β
A.1
B.2
C.3
D.4
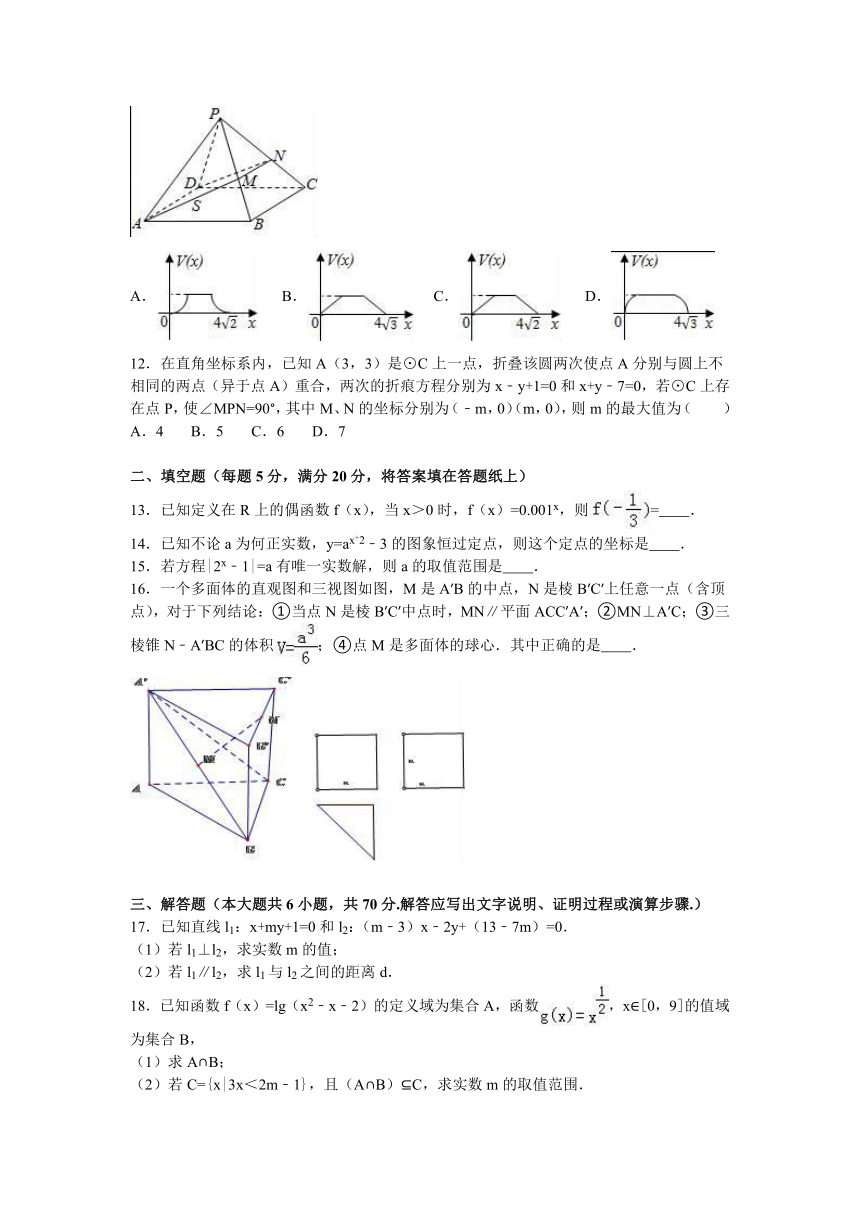
11.在四棱锥P﹣ABCD中,各侧面是全等的等腰三角形,腰长为4且顶角为30°,底面是正方形(如图),在棱PB,PC上各有一点M、N,且四边形AMND的周长最小,点S从A出发依次沿四边形AM,MN,ND运动至点D,记点S行进的路程为x,棱锥S﹣ABCD的体积为V(x),则函数V(x)的图象是( )
A.
B.
C.
D.
12.在直角坐标系内,已知A(3,3)是⊙C上一点,折叠该圆两次使点A分别与圆上不相同的两点(异于点A)重合,两次的折痕方程分别为x﹣y+1=0和x+y﹣7=0,若⊙C上存在点P,使∠MPN=90°,其中M、N的坐标分别为(﹣m,0)(m,0),则m的最大值为( )
A.4
B.5
C.6
D.7
二、填空题(每题5分,满分20分,将答案填在答题纸上)
13.已知定义在R上的偶函数f(x),当x>0时,f(x)=0.001x,则= .
14.已知不论a为何正实数,y=ax+2﹣3的图象恒过定点,则这个定点的坐标是 .
15.若方程|2x﹣1|=a有唯一实数解,则a的取值范围是 .
16.一个多面体的直观图和三视图如图,M是A′B的中点,N是棱B′C′上任意一点(含顶点),对于下列结论:①当点N是棱B′C′中点时,MN∥平面ACC′A′;②MN⊥A′C;③三棱锥N﹣A′BC的体积;④点M是多面体的球心.其中正确的是 .
三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)
17.已知直线l1:x+my+1=0和l2:(m﹣3)x﹣2y+(13﹣7m)=0.
(1)若l1⊥l2,求实数m的值;
(2)若l1∥l2,求l1与l2之间的距离d.
18.已知函数f(x)=lg(x2﹣x﹣2)的定义域为集合A,函数,x∈[0,9]的值域为集合B,
(1)求A∩B;
(2)若C={x|3x<2m﹣1},且(A∩B) C,求实数m的取值范围.
19.如图,△PAD与正方形ABCD共用一边AD,平面PAD⊥平面ABCD,其中PA=PD,AB=2,点E是棱PA的中点.
(1)求证:PC∥平面BDE;
(2)若直线PA与平面ABCD所成角为60°,求点A到平面BDE的距离.
20.已知函数.
(1)判断f(x)的奇偶性;
(2)当x∈[﹣1,1]时,f(x)≥m恒成立,求m的取值范围.
21.已知点A(6,2),B(3,2),动点M满足|MA|=2|MB|.
(1)求点M的轨迹方程;
(2)设M的轨迹与y轴的交点为P,过P作斜率为k的直线l与M的轨迹交于另一点Q,若C(1,2k+2),求△CPQ面积的最大值,并求出此时直线l的方程.
22.已知函数f(x)=ax2+bx+c(a,b,c∈R且a≠0),若对任意实数x,不等式2x≤f(x)(x+1)2恒成立.
(1)求f(1)的值;
(2)求a的取值范围;
(3)若函数g(x)=f(x)+2a|x﹣1|,x∈[﹣2,2]的最小值为﹣1,求a的值.
2015-2016学年湖南省常德市石门一中高一(下)入学数学试卷
参考答案与试题解析
一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合M={1,2,3},N={2,3,4},则( )
A.M N
B.N M
C.M∩N={2,3}
D.M∪N={2,4}
【考点】交集及其运算;并集及其运算.
【分析】由M与N,求出两集合的交集、并集,即可作出判断.
【解答】解:∵M={1,2,3},N={2,3,4},
两集合不存在包含关系,
∴M∩N={2,3},M∪N={1,2,3,4},
故选:C.
2.已知函数,那么f[f()]的值为( )
A.9
B.
C.﹣9
D.﹣
【考点】函数的值.
【分析】首先判断自变量是属于哪个区间,再代入相应的解析式,进而求出答案.
【解答】解:∵,∴==﹣2,
而﹣2<0,∴f(﹣2)=3﹣2=.
∴=.
故选B.
3.在直角坐标系中,下列直线中倾斜角为钝角的是( )
A.y=3x﹣1
B.x+2=0
C.
+=1
D.2x﹣y+1=0
【考点】直线的倾斜角.
【分析】根据斜率的正负判断其倾斜角的范围即可.
【解答】解:对于A:k=3,是锐角,
对于B:是直角,
对于C:k=﹣,是钝角,
对于D:k=2,是锐角,
故选:C.
4.线段x﹣2y+1=0(﹣1≤x≤3)的垂直平分线方程为( )
A.x+2y﹣3=0
B.2x+y﹣3=0
C.2x+y﹣1=0
D.2x﹣y﹣1=0
【考点】直线的一般式方程与直线的垂直关系.
【分析】求出线段的中点坐标,求出线段的垂直平分线的斜率,然后求出垂直平分线方程.
【解答】解:x=﹣1时,y=0,x=3时,y=2,
∴(﹣1,0),(3,2)的中点为(1,1),
线段x﹣2y+1=0的斜率是:k==,
线段x﹣2y+1=0(﹣1≤x≤3)的垂直平分线的斜率是:﹣2,
故所求直线方程是:y﹣1=﹣2(x﹣1),
即:2x+y﹣3=0,
故选:B.
5.函数f(x)=x﹣3+log3x的零点所在区间是( )
A.(0,1)
B.(1,2)
C.(2,3)
D.(3,+∞)
【考点】函数零点的判定定理.
【分析】计算各区间端点的函数值,根据零点的存在性定理判断.
【解答】解:f(x)在(0,+∞)上为增函数,
且f(1)=﹣2<0,f(2)=﹣1+log32<﹣1+log33=0,f(3)=log33=1>0,
∴f(2)f(3)<0,
∴f(x)的零点所在区间为(2,3).
故选:C.
6.已知a、b∈R,且满足0<a<1<b,则下列大小关系正确的是( )
A.ab<ba<logab
B.ba<logab<ab
C.logab<ba<ab
D.logab<ab<ba
【考点】对数值大小的比较.
【分析】利用指数函数、对数函数的单调性求解.
【解答】解:∵a、b∈R,且满足0<a<1<b,
∴logab<loga1=0,
ba>b0=a0>ab>0,
∴logab<ab<ba.
故选:D.
7.函数f(x)=(1﹣x)|x﹣3|在(﹣∞,a]上取得最小值﹣1,则实数a的取值范围是( )
A.(﹣∞,2]
B.
C.
D.[2,+∞)
【考点】函数的最值及其几何意义;分段函数的应用.
【分析】由零点分段法,我们可将函数f(x)=(1﹣x)|x﹣3|的解析式化为分段函数的形式,然后根据分段函数分段处理的原则,画出函数的图象,进而结合图象数形结合,可得实数a的集合
【解答】解:∵函数f(x)=(1﹣x)|x﹣3|=,
其函数图象如下图所示:
由函数图象可得:
函数f(x)=(1﹣x)|x﹣3|在(﹣∞,a]上取得最小值﹣1,
当x≥3时,f(x)=﹣x2+4x﹣3=﹣1,解得x=2+,
当x<3时,f(x)=x2﹣4x+3=﹣1,解得x=2,
实数a须满足2≤a≤2+.
故实数a的集合是[2,2+].
故选:C.
8.设奇函数f(x)在(0,+∞)上为增函数,且,则不等式x[f(x)﹣f(﹣x)]<0的解集为( )
A.
B.
C.
D.
【考点】奇偶性与单调性的综合.
【分析】根据条件可以得到f(x)在(﹣∞,0)上为增函数,且,f(x)为奇函数,便有f(﹣x)=﹣f(x),从而不等式x[f(x)﹣f(﹣x)]<0可变成xf(x)<0,从而可得到,或,根据f(x)的单调性便可解出这两个不等式组,从而便求出原不等式的解集.
【解答】解:f(x)为奇函数,在(0,+∞)上为增函数;
∴f(x)在(﹣∞,0)上为增函数;
∵f()=0,∴;
由x[f(x)﹣f(﹣x)]<0得,2xf(x)<0;
∴xf(x)<0;
∴,或;
即,或;
根据f(x)的单调性解得,或;
∴原不等式的解集为.
故选:B.
9.用半径为R的半圆卷成一个无底圆锥,则这个无底圆锥的体积为( )
A.
B.
C.
D.
【考点】旋转体(圆柱、圆锥、圆台).
【分析】一个圆锥的侧面展开图是一个扇形,这个扇形的弧长等于底面圆的周长.由此可得底面圆的半径r=R,从而得到圆锥的高h=,最后用锥体的体积公式得到这个无底圆锥的体积.
【解答】解:根据题意,设无底圆锥的底面圆半径为r,则底面圆的周长等于侧面展开图的半圆弧长
∴2πr=πR,可得r=R圆锥的高h==
根据圆锥的体积公式,可得V=S底 h=π(R)2 =
故选A
10.给出下面四个命题(其中m,n,l是空间中不同的直线,α,β是空间中不同的平面)中错误的命题个数为( )
①m∥n,n∥α m∥α
②α⊥β,α∩β=m,l⊥m l⊥β
③l⊥m,l⊥n,m α,n α l⊥α
④m∩n=A,m∥α,m∥β,n∥α,n∥β α∥β
A.1
B.2
C.3
D.4
【考点】命题的真假判断与应用.
【分析】①根据线面平行的判定定理进行判断,
②根据线面垂直的性质进行判断,
③跟姐姐线面垂直的性质进行判断,
④跟姐姐面面平行的判定定理和性质进行判断.
【解答】解:①m∥n,n∥α m∥α或m α,故①错误,
②α⊥β,α∩β=m,l⊥m l⊥β或l β或l与β相交,故②错误
③当m与n相交时,l⊥α,当m与n不相交时,l⊥α不成立,故③错误,
④m∩n=A,设经过m,n的平面为γ,
∵m∥α,n∥α,∴α∥γ,
∵m∥β,n∥β β∥γ,则α∥β成立,故④正确,
故错误的是①②③,
故选:C
11.在四棱锥P﹣ABCD中,各侧面是全等的等腰三角形,腰长为4且顶角为30°,底面是正方形(如图),在棱PB,PC上各有一点M、N,且四边形AMND的周长最小,点S从A出发依次沿四边形AM,MN,ND运动至点D,记点S行进的路程为x,棱锥S﹣ABCD的体积为V(x),则函数V(x)的图象是( )
A.
B.
C.
D.
【考点】函数的图象.
【分析】根据棱锥的体积公式求出函数的解析式,并根据正四棱锥侧面展开图,从A到D最短距离为直角三角形PAD的斜边为4,求出x的范围,判断函数的图象即可.
【解答】解:四棱锥P﹣ABCD中,各侧面是全等的等腰三角形,腰长为4且顶角为30°,
∴BC2=PB2+PC2﹣2PB PCcos30°=16+16﹣2×4×4×=32﹣16,
∴底面正方形的面积s=32﹣16,h=xtan30°,
∴V(x)=sh=xtan30°,为线性函数,
∵四边形AMND的周长最小,正四棱锥侧面展开图如图所示,
∴正四棱锥侧面展开图,从A到D最短距离为直角三角形PAD的斜边为4,
∴x≤4
故选:C.
12.在直角坐标系内,已知A(3,3)是⊙C上一点,折叠该圆两次使点A分别与圆上不相同的两点(异于点A)重合,两次的折痕方程分别为x﹣y+1=0和x+y﹣7=0,若⊙C上存在点P,使∠MPN=90°,其中M、N的坐标分别为(﹣m,0)(m,0),则m的最大值为( )
A.4
B.5
C.6
D.7
【考点】直线与圆的位置关系.
【分析】求出⊙C的方程,过P,M,N的圆的方程,两圆外切时,m取得最大值.
【解答】解:由题意,∴A(3,3)是⊙C上一点,折叠该圆两次使点A分别与圆上不相同的两点(异于点A)重合,两次的折痕方程分别为x﹣y+1=0和x+y﹣7=0,
∴圆上不相同的两点为B(2,4,),D(4,4),
∵A(3,3),BA⊥DA
∴BD的中点为圆心C(3,4),半径为1,
∴⊙C的方程为(x﹣3)2+(y﹣4)2=1.
过P,M,N的圆的方程为x2+y2=m2,
∴两圆外切时,m的最大值为+1=6,
故选:C.
二、填空题(每题5分,满分20分,将答案填在答题纸上)
13.已知定义在R上的偶函数f(x),当x>0时,f(x)=0.001x,则= .
【考点】函数奇偶性的性质.
【分析】先由函数是偶函数得f(﹣x)=f(x),再利用x>0时,f(x)=0.001x,即可求出.
【解答】解:∵函数y=f(x)是偶函数,
∴f(﹣x)=f(x),
∵x>0时,f(x)=0.001x,
∴=f()=.
故答案为:.
14.已知不论a为何正实数,y=ax+2﹣3的图象恒过定点,则这个定点的坐标是 (﹣2,﹣2) .
【考点】指数函数的图象变换.
【分析】令x+2=0,则由a0=1恒成立可得答案.
【解答】解:令x+2=0,则x=﹣2,y=﹣2,
故y=ax+2﹣3的图象恒过定点(﹣2,﹣2),
故答案为:(﹣2,﹣2)
15.若方程|2x﹣1|=a有唯一实数解,则a的取值范围是 a≥1或a=0 .
【考点】根的存在性及根的个数判断.
【分析】作函数y=|2x﹣1|的图象,从而结合图象讨论方程的根的个数即可.
【解答】解:作函数y=|2x﹣1|的图象如下,
,
结合图象可知,
当a=0时,方程|2x﹣1|=a有唯一实数解,
当0<a<1时,方程|2x﹣1|=a有两个实数解,
当a≥1时,方程|2x﹣1|=a有唯一实数解,
故答案为:a≥1或a=0.
16.一个多面体的直观图和三视图如图,M是A′B的中点,N是棱B′C′上任意一点(含顶点),对于下列结论:①当点N是棱B′C′中点时,MN∥平面ACC′A′;②MN⊥A′C;③三棱锥N﹣A′BC的体积;④点M是多面体的球心.其中正确的是 ①②③④ .
【考点】棱柱、棱锥、棱台的体积;直线与平面平行的判定;直线与平面垂直的性质.
【分析】本题是直观图和三视图的综合分析题,要抓住M是A′B的中点,N是棱B′C′上的任意一点(含顶点)就是动点,从三视图抓住直观图的特征,结合下情况分别判断即可得答案.
【解答】解:①M连接AB中点E,N连接BC中点F,得到MNFE平行于平面ACC′A′,面面平行即可得到线面平行,故①正确;
②M连接A′C中点G,连接C′G,A′C⊥平面MNC′G.∴MN⊥A′C,故②正确;
③三棱锥N﹣A′BC的体积为= S△BCA′ MB′= CA′ BC MB′=,故③正确;
④由三视图可知:此多面体是正方体切割下来了的,M是A′B的中点(空间对角线中点),是正方体中心,∴点M是该多面体外接球的球心.故④正确.
∴正确的是①②③④.
故答案为:①②③④.
三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)
17.已知直线l1:x+my+1=0和l2:(m﹣3)x﹣2y+(13﹣7m)=0.
(1)若l1⊥l2,求实数m的值;
(2)若l1∥l2,求l1与l2之间的距离d.
【考点】两条平行直线间的距离;直线的一般式方程与直线的垂直关系.
【分析】(1)由垂直可得1 (m﹣3)﹣2m=0,解方程可得;
(2)由l1∥l2可得m值,可得直线方程,由平行线间的距离公式可得.
【解答】解:(1)∵直线l1:x+my+1=0和l2:(m﹣3)x﹣2y+(13﹣7m)=0,
∴当l1⊥l2时,1 (m﹣3)﹣2m=0,解得m=﹣3;
(2)由l1∥l2可得m(m﹣3)+2=0,解得m=1或m=﹣2,
当m=2时,l1与l2重合,应舍去,
当m=1时,可得l1:x+y+1=0,l2:﹣2x﹣2y+6=0,即x+y﹣3=0,
由平行线间的距离公式可得d==2
18.已知函数f(x)=lg(x2﹣x﹣2)的定义域为集合A,函数,x∈[0,9]的值域为集合B,
(1)求A∩B;
(2)若C={x|3x<2m﹣1},且(A∩B) C,求实数m的取值范围.
【考点】集合的包含关系判断及应用;交集及其运算.
【分析】(1)由对数函数的定义域求出集合A,由函数,x∈[0,9]的值域求出集合B,则A∩B可求;
(2)由集合C化为且(A∩B) C得到不等式,求解不等式即可得到实数m的取值范围.
【解答】解:(1)已知函数f(x)=lg(x2﹣x﹣2)的定义域为集合A,函数,x∈[0,9]的值域为集合B,
则A={x|x2﹣x﹣2>0}={x|x<﹣1或x>2},B={x|0≤x≤3},
∴A∩B={x|x<﹣1或x>2}∩{x|0≤x≤3}={x|2<x≤3};
(2)∵且(A∩B) C,
∴,即m>5.
19.如图,△PAD与正方形ABCD共用一边AD,平面PAD⊥平面ABCD,其中PA=PD,AB=2,点E是棱PA的中点.
(1)求证:PC∥平面BDE;
(2)若直线PA与平面ABCD所成角为60°,求点A到平面BDE的距离.
【考点】点、线、面间的距离计算;直线与平面平行的判定.
【分析】(1)连接AC,交BD于O,连接EO,证明PC∥OE,即可证明PC∥平面BDE;
(2)取AD的中点N,连接PN,证明∠PAN为直线PA与平面ABCD所成角,利用等体积方法求点A到平面BDE的距离.
【解答】(1)证明:连接AC,交BD于O,连接EO,则
∵ABCD是正方形,
∴O是AC的中点,
∵点E是棱PA的中点,
∴PC∥OE,
∵OE 平面BDE,BD 平面BDE,
∴PC∥平面BDE;
(2)解:取AD的中点N,连接PN,则
∵PA=PD,
∴PN⊥AD,
∵平面PAD∩平面ABCD=AD,
∴PN⊥平面ABCD,
∴∠PAN为直线PA与平面ABCD所成角∴∠PAN=60°∴PA=PD=AD=2,
∵AB⊥AD,平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,
∴AB⊥平面PAD,
∴VB﹣DAE==,
Rt△EAB中,EA=1,AB=2,BE=,
∵,BD=2,
∴DE⊥EB,
∴S△BDE==.
设点A到平面BDE的距离为h.则,
∴h=,
∴点A到平面BDE的距离为.
20.已知函数.
(1)判断f(x)的奇偶性;
(2)当x∈[﹣1,1]时,f(x)≥m恒成立,求m的取值范围.
【考点】函数恒成立问题;函数奇偶性的判断.
【分析】(1)根据函数奇偶性的定义判断即可;(2)根据函数单调性的定义判断其单调性,从而求出函数的最小值,求出m的范围.
【解答】解:(1)在函数f(x)的定义域R上任取一自变量x
因为=﹣f(x),
所以函数f(x)为奇函数;┅
(2)当a>1时,在[﹣1,1]上任取x1,x2,令x1<x2,
=,
∵0≤x1<x2≤1,
∴f(x1)﹣f(x2)<0
所以函数f(x)在x∈[﹣1,1]时为增函数,┅
当0<a<1时,同理可证函数f(x)在x∈[﹣1,1]时为增函数,
,
所以m≤1┅
21.已知点A(6,2),B(3,2),动点M满足|MA|=2|MB|.
(1)求点M的轨迹方程;
(2)设M的轨迹与y轴的交点为P,过P作斜率为k的直线l与M的轨迹交于另一点Q,若C(1,2k+2),求△CPQ面积的最大值,并求出此时直线l的方程.
【考点】直线与圆锥曲线的综合问题;轨迹方程.
【分析】(1)设M(x,y),由|MA|=2|MB|,利用两点之间的距离公式即可得出.
(2)令x=0,可得P(0,2).直线l的方程为:y=kx+2,(k≠0)代入圆的方程可得:(1+k2)x2﹣4x=0,解出可得Q坐标,|PQ|.求出点C到直线l的距离d,△CPQ面积S=|PQ| d,再利用基本不等式的性质即可得出.
【解答】解:(1)设M(x,y),∵|MA|=2|MB|,
∴=2,
化为:(x﹣2)2+(y﹣2)2=4.
(2)令x=0,解得y=2,∴P(0,2).
直线l的方程为:y=kx+2,(k≠0)代入圆的方程可得:(1+k2)x2﹣4x=0,
解得x=0,或x=.
∴Q.
∴|PQ|==.
点C到直线l的距离d==.
∴△CPQ面积S=|PQ| d=××==≤=1,当且仅当|k|=1时取等号.
∴△CPQ面积的最大值1时,此时直线l的方程为:y=±x+2.
22.已知函数f(x)=ax2+bx+c(a,b,c∈R且a≠0),若对任意实数x,不等式2x≤f(x)(x+1)2恒成立.
(1)求f(1)的值;
(2)求a的取值范围;
(3)若函数g(x)=f(x)+2a|x﹣1|,x∈[﹣2,2]的最小值为﹣1,求a的值.
【考点】二次函数的性质.
【分析】(1)在给出的不等式中,令x=1,根据这个条件可求出f(1)的值;
(2)联立f(1)=2,即可求出a+c与b的关系式.由f(x)﹣2x≥0恒成立,即:ax2+(b﹣1)x+c≥0对于一切实数x恒成立,只有当a>0,且△=(b﹣2)2﹣4ac≤0时,求得a=c>0,再由f(x)(x+1)2恒成立,可得二次项系数小于0,判别式小于等于0,解不等式即可得到a的范围;
(3)讨论当1≤x≤2时,当﹣2≤x<1时,去掉绝对值,运用二次函数的对称轴和区间的关系,求得最小值,解方程可得a的值.
【解答】解:(1)令x=1,由2x≤f(x)(x+1)2可得,
2≤f(1)≤2,∴f(1)=2;
(2)由f(1)=2可得a+b+c=2,即为b=2﹣(a+c),
∵对于一切实数x,f(x)﹣2x≥0恒成立,
∴ax2+(b﹣2)x+c≥0(a≠0)对于一切实数x恒成立,
∴,即.
可得(a﹣c)2≤0,但(a﹣c)2≥0,即有a=c>0,
则f(x)=ax2+bx+a,
f(x)(x+1)2恒成立,即为(a﹣)x2+(b﹣1)x+(a﹣)≤0,
可得a﹣<0,且△=(b﹣1)2﹣4(a﹣)2≤0,
由b﹣1=1﹣2a,即有△=0成立;
综上可得a的范围是(0,);
(3)函数g(x)=f(x)+2a|x﹣1|=ax2+(2﹣2a)x+a+2a|x﹣1|(0<a<),
当1≤x≤2时,g(x)=ax2+2x﹣a在[1,2]递增,可得x=1时,取得最小值2;
当﹣2≤x<1时,g(x)=ax2+(2﹣4a)x+3a,对称轴为x=,
当≤﹣2,即为0<a≤时,[﹣2,1)递增,
可得x=﹣2取得最小值,且为4a﹣4+8a+3a=﹣1,解得a=;
当>﹣2,即<a<时,
x=,取得最小值,且为=﹣1,
解得a= (,).
综上可得,a=.
2016年11月4日
一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合M={1,2,3},N={2,3,4},则( )
A.M N
B.N M
C.M∩N={2,3}
D.M∪N={2,4}
2.已知函数,那么f[f()]的值为( )
A.9
B.
C.﹣9
D.﹣
3.在直角坐标系中,下列直线中倾斜角为钝角的是( )
A.y=3x﹣1
B.x+2=0
C.
+=1
D.2x﹣y+1=0
4.线段x﹣2y+1=0(﹣1≤x≤3)的垂直平分线方程为( )
A.x+2y﹣3=0
B.2x+y﹣3=0
C.2x+y﹣1=0
D.2x﹣y﹣1=0
5.函数f(x)=x﹣3+log3x的零点所在区间是( )
A.(0,1)
B.(1,2)
C.(2,3)
D.(3,+∞)
6.已知a、b∈R,且满足0<a<1<b,则下列大小关系正确的是( )
A.ab<ba<logab
B.ba<logab<ab
C.logab<ba<ab
D.logab<ab<ba
7.函数f(x)=(1﹣x)|x﹣3|在(﹣∞,a]上取得最小值﹣1,则实数a的取值范围是( )
A.(﹣∞,2]
B.
C.
D.[2,+∞)
8.设奇函数f(x)在(0,+∞)上为增函数,且,则不等式x[f(x)﹣f(﹣x)]<0的解集为( )
A.
B.
C.
D.
9.用半径为R的半圆卷成一个无底圆锥,则这个无底圆锥的体积为( )
A.
B.
C.
D.
10.给出下面四个命题(其中m,n,l是空间中不同的直线,α,β是空间中不同的平面)中错误的命题个数为( )
①m∥n,n∥α m∥α
②α⊥β,α∩β=m,l⊥m l⊥β
③l⊥m,l⊥n,m α,n α l⊥α
④m∩n=A,m∥α,m∥β,n∥α,n∥β α∥β
A.1
B.2
C.3
D.4
11.在四棱锥P﹣ABCD中,各侧面是全等的等腰三角形,腰长为4且顶角为30°,底面是正方形(如图),在棱PB,PC上各有一点M、N,且四边形AMND的周长最小,点S从A出发依次沿四边形AM,MN,ND运动至点D,记点S行进的路程为x,棱锥S﹣ABCD的体积为V(x),则函数V(x)的图象是( )
A.
B.
C.
D.
12.在直角坐标系内,已知A(3,3)是⊙C上一点,折叠该圆两次使点A分别与圆上不相同的两点(异于点A)重合,两次的折痕方程分别为x﹣y+1=0和x+y﹣7=0,若⊙C上存在点P,使∠MPN=90°,其中M、N的坐标分别为(﹣m,0)(m,0),则m的最大值为( )
A.4
B.5
C.6
D.7
二、填空题(每题5分,满分20分,将答案填在答题纸上)
13.已知定义在R上的偶函数f(x),当x>0时,f(x)=0.001x,则= .
14.已知不论a为何正实数,y=ax+2﹣3的图象恒过定点,则这个定点的坐标是 .
15.若方程|2x﹣1|=a有唯一实数解,则a的取值范围是 .
16.一个多面体的直观图和三视图如图,M是A′B的中点,N是棱B′C′上任意一点(含顶点),对于下列结论:①当点N是棱B′C′中点时,MN∥平面ACC′A′;②MN⊥A′C;③三棱锥N﹣A′BC的体积;④点M是多面体的球心.其中正确的是 .
三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)
17.已知直线l1:x+my+1=0和l2:(m﹣3)x﹣2y+(13﹣7m)=0.
(1)若l1⊥l2,求实数m的值;
(2)若l1∥l2,求l1与l2之间的距离d.
18.已知函数f(x)=lg(x2﹣x﹣2)的定义域为集合A,函数,x∈[0,9]的值域为集合B,
(1)求A∩B;
(2)若C={x|3x<2m﹣1},且(A∩B) C,求实数m的取值范围.
19.如图,△PAD与正方形ABCD共用一边AD,平面PAD⊥平面ABCD,其中PA=PD,AB=2,点E是棱PA的中点.
(1)求证:PC∥平面BDE;
(2)若直线PA与平面ABCD所成角为60°,求点A到平面BDE的距离.
20.已知函数.
(1)判断f(x)的奇偶性;
(2)当x∈[﹣1,1]时,f(x)≥m恒成立,求m的取值范围.
21.已知点A(6,2),B(3,2),动点M满足|MA|=2|MB|.
(1)求点M的轨迹方程;
(2)设M的轨迹与y轴的交点为P,过P作斜率为k的直线l与M的轨迹交于另一点Q,若C(1,2k+2),求△CPQ面积的最大值,并求出此时直线l的方程.
22.已知函数f(x)=ax2+bx+c(a,b,c∈R且a≠0),若对任意实数x,不等式2x≤f(x)(x+1)2恒成立.
(1)求f(1)的值;
(2)求a的取值范围;
(3)若函数g(x)=f(x)+2a|x﹣1|,x∈[﹣2,2]的最小值为﹣1,求a的值.
2015-2016学年湖南省常德市石门一中高一(下)入学数学试卷
参考答案与试题解析
一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合M={1,2,3},N={2,3,4},则( )
A.M N
B.N M
C.M∩N={2,3}
D.M∪N={2,4}
【考点】交集及其运算;并集及其运算.
【分析】由M与N,求出两集合的交集、并集,即可作出判断.
【解答】解:∵M={1,2,3},N={2,3,4},
两集合不存在包含关系,
∴M∩N={2,3},M∪N={1,2,3,4},
故选:C.
2.已知函数,那么f[f()]的值为( )
A.9
B.
C.﹣9
D.﹣
【考点】函数的值.
【分析】首先判断自变量是属于哪个区间,再代入相应的解析式,进而求出答案.
【解答】解:∵,∴==﹣2,
而﹣2<0,∴f(﹣2)=3﹣2=.
∴=.
故选B.
3.在直角坐标系中,下列直线中倾斜角为钝角的是( )
A.y=3x﹣1
B.x+2=0
C.
+=1
D.2x﹣y+1=0
【考点】直线的倾斜角.
【分析】根据斜率的正负判断其倾斜角的范围即可.
【解答】解:对于A:k=3,是锐角,
对于B:是直角,
对于C:k=﹣,是钝角,
对于D:k=2,是锐角,
故选:C.
4.线段x﹣2y+1=0(﹣1≤x≤3)的垂直平分线方程为( )
A.x+2y﹣3=0
B.2x+y﹣3=0
C.2x+y﹣1=0
D.2x﹣y﹣1=0
【考点】直线的一般式方程与直线的垂直关系.
【分析】求出线段的中点坐标,求出线段的垂直平分线的斜率,然后求出垂直平分线方程.
【解答】解:x=﹣1时,y=0,x=3时,y=2,
∴(﹣1,0),(3,2)的中点为(1,1),
线段x﹣2y+1=0的斜率是:k==,
线段x﹣2y+1=0(﹣1≤x≤3)的垂直平分线的斜率是:﹣2,
故所求直线方程是:y﹣1=﹣2(x﹣1),
即:2x+y﹣3=0,
故选:B.
5.函数f(x)=x﹣3+log3x的零点所在区间是( )
A.(0,1)
B.(1,2)
C.(2,3)
D.(3,+∞)
【考点】函数零点的判定定理.
【分析】计算各区间端点的函数值,根据零点的存在性定理判断.
【解答】解:f(x)在(0,+∞)上为增函数,
且f(1)=﹣2<0,f(2)=﹣1+log32<﹣1+log33=0,f(3)=log33=1>0,
∴f(2)f(3)<0,
∴f(x)的零点所在区间为(2,3).
故选:C.
6.已知a、b∈R,且满足0<a<1<b,则下列大小关系正确的是( )
A.ab<ba<logab
B.ba<logab<ab
C.logab<ba<ab
D.logab<ab<ba
【考点】对数值大小的比较.
【分析】利用指数函数、对数函数的单调性求解.
【解答】解:∵a、b∈R,且满足0<a<1<b,
∴logab<loga1=0,
ba>b0=a0>ab>0,
∴logab<ab<ba.
故选:D.
7.函数f(x)=(1﹣x)|x﹣3|在(﹣∞,a]上取得最小值﹣1,则实数a的取值范围是( )
A.(﹣∞,2]
B.
C.
D.[2,+∞)
【考点】函数的最值及其几何意义;分段函数的应用.
【分析】由零点分段法,我们可将函数f(x)=(1﹣x)|x﹣3|的解析式化为分段函数的形式,然后根据分段函数分段处理的原则,画出函数的图象,进而结合图象数形结合,可得实数a的集合
【解答】解:∵函数f(x)=(1﹣x)|x﹣3|=,
其函数图象如下图所示:
由函数图象可得:
函数f(x)=(1﹣x)|x﹣3|在(﹣∞,a]上取得最小值﹣1,
当x≥3时,f(x)=﹣x2+4x﹣3=﹣1,解得x=2+,
当x<3时,f(x)=x2﹣4x+3=﹣1,解得x=2,
实数a须满足2≤a≤2+.
故实数a的集合是[2,2+].
故选:C.
8.设奇函数f(x)在(0,+∞)上为增函数,且,则不等式x[f(x)﹣f(﹣x)]<0的解集为( )
A.
B.
C.
D.
【考点】奇偶性与单调性的综合.
【分析】根据条件可以得到f(x)在(﹣∞,0)上为增函数,且,f(x)为奇函数,便有f(﹣x)=﹣f(x),从而不等式x[f(x)﹣f(﹣x)]<0可变成xf(x)<0,从而可得到,或,根据f(x)的单调性便可解出这两个不等式组,从而便求出原不等式的解集.
【解答】解:f(x)为奇函数,在(0,+∞)上为增函数;
∴f(x)在(﹣∞,0)上为增函数;
∵f()=0,∴;
由x[f(x)﹣f(﹣x)]<0得,2xf(x)<0;
∴xf(x)<0;
∴,或;
即,或;
根据f(x)的单调性解得,或;
∴原不等式的解集为.
故选:B.
9.用半径为R的半圆卷成一个无底圆锥,则这个无底圆锥的体积为( )
A.
B.
C.
D.
【考点】旋转体(圆柱、圆锥、圆台).
【分析】一个圆锥的侧面展开图是一个扇形,这个扇形的弧长等于底面圆的周长.由此可得底面圆的半径r=R,从而得到圆锥的高h=,最后用锥体的体积公式得到这个无底圆锥的体积.
【解答】解:根据题意,设无底圆锥的底面圆半径为r,则底面圆的周长等于侧面展开图的半圆弧长
∴2πr=πR,可得r=R圆锥的高h==
根据圆锥的体积公式,可得V=S底 h=π(R)2 =
故选A
10.给出下面四个命题(其中m,n,l是空间中不同的直线,α,β是空间中不同的平面)中错误的命题个数为( )
①m∥n,n∥α m∥α
②α⊥β,α∩β=m,l⊥m l⊥β
③l⊥m,l⊥n,m α,n α l⊥α
④m∩n=A,m∥α,m∥β,n∥α,n∥β α∥β
A.1
B.2
C.3
D.4
【考点】命题的真假判断与应用.
【分析】①根据线面平行的判定定理进行判断,
②根据线面垂直的性质进行判断,
③跟姐姐线面垂直的性质进行判断,
④跟姐姐面面平行的判定定理和性质进行判断.
【解答】解:①m∥n,n∥α m∥α或m α,故①错误,
②α⊥β,α∩β=m,l⊥m l⊥β或l β或l与β相交,故②错误
③当m与n相交时,l⊥α,当m与n不相交时,l⊥α不成立,故③错误,
④m∩n=A,设经过m,n的平面为γ,
∵m∥α,n∥α,∴α∥γ,
∵m∥β,n∥β β∥γ,则α∥β成立,故④正确,
故错误的是①②③,
故选:C
11.在四棱锥P﹣ABCD中,各侧面是全等的等腰三角形,腰长为4且顶角为30°,底面是正方形(如图),在棱PB,PC上各有一点M、N,且四边形AMND的周长最小,点S从A出发依次沿四边形AM,MN,ND运动至点D,记点S行进的路程为x,棱锥S﹣ABCD的体积为V(x),则函数V(x)的图象是( )
A.
B.
C.
D.
【考点】函数的图象.
【分析】根据棱锥的体积公式求出函数的解析式,并根据正四棱锥侧面展开图,从A到D最短距离为直角三角形PAD的斜边为4,求出x的范围,判断函数的图象即可.
【解答】解:四棱锥P﹣ABCD中,各侧面是全等的等腰三角形,腰长为4且顶角为30°,
∴BC2=PB2+PC2﹣2PB PCcos30°=16+16﹣2×4×4×=32﹣16,
∴底面正方形的面积s=32﹣16,h=xtan30°,
∴V(x)=sh=xtan30°,为线性函数,
∵四边形AMND的周长最小,正四棱锥侧面展开图如图所示,
∴正四棱锥侧面展开图,从A到D最短距离为直角三角形PAD的斜边为4,
∴x≤4
故选:C.
12.在直角坐标系内,已知A(3,3)是⊙C上一点,折叠该圆两次使点A分别与圆上不相同的两点(异于点A)重合,两次的折痕方程分别为x﹣y+1=0和x+y﹣7=0,若⊙C上存在点P,使∠MPN=90°,其中M、N的坐标分别为(﹣m,0)(m,0),则m的最大值为( )
A.4
B.5
C.6
D.7
【考点】直线与圆的位置关系.
【分析】求出⊙C的方程,过P,M,N的圆的方程,两圆外切时,m取得最大值.
【解答】解:由题意,∴A(3,3)是⊙C上一点,折叠该圆两次使点A分别与圆上不相同的两点(异于点A)重合,两次的折痕方程分别为x﹣y+1=0和x+y﹣7=0,
∴圆上不相同的两点为B(2,4,),D(4,4),
∵A(3,3),BA⊥DA
∴BD的中点为圆心C(3,4),半径为1,
∴⊙C的方程为(x﹣3)2+(y﹣4)2=1.
过P,M,N的圆的方程为x2+y2=m2,
∴两圆外切时,m的最大值为+1=6,
故选:C.
二、填空题(每题5分,满分20分,将答案填在答题纸上)
13.已知定义在R上的偶函数f(x),当x>0时,f(x)=0.001x,则= .
【考点】函数奇偶性的性质.
【分析】先由函数是偶函数得f(﹣x)=f(x),再利用x>0时,f(x)=0.001x,即可求出.
【解答】解:∵函数y=f(x)是偶函数,
∴f(﹣x)=f(x),
∵x>0时,f(x)=0.001x,
∴=f()=.
故答案为:.
14.已知不论a为何正实数,y=ax+2﹣3的图象恒过定点,则这个定点的坐标是 (﹣2,﹣2) .
【考点】指数函数的图象变换.
【分析】令x+2=0,则由a0=1恒成立可得答案.
【解答】解:令x+2=0,则x=﹣2,y=﹣2,
故y=ax+2﹣3的图象恒过定点(﹣2,﹣2),
故答案为:(﹣2,﹣2)
15.若方程|2x﹣1|=a有唯一实数解,则a的取值范围是 a≥1或a=0 .
【考点】根的存在性及根的个数判断.
【分析】作函数y=|2x﹣1|的图象,从而结合图象讨论方程的根的个数即可.
【解答】解:作函数y=|2x﹣1|的图象如下,
,
结合图象可知,
当a=0时,方程|2x﹣1|=a有唯一实数解,
当0<a<1时,方程|2x﹣1|=a有两个实数解,
当a≥1时,方程|2x﹣1|=a有唯一实数解,
故答案为:a≥1或a=0.
16.一个多面体的直观图和三视图如图,M是A′B的中点,N是棱B′C′上任意一点(含顶点),对于下列结论:①当点N是棱B′C′中点时,MN∥平面ACC′A′;②MN⊥A′C;③三棱锥N﹣A′BC的体积;④点M是多面体的球心.其中正确的是 ①②③④ .
【考点】棱柱、棱锥、棱台的体积;直线与平面平行的判定;直线与平面垂直的性质.
【分析】本题是直观图和三视图的综合分析题,要抓住M是A′B的中点,N是棱B′C′上的任意一点(含顶点)就是动点,从三视图抓住直观图的特征,结合下情况分别判断即可得答案.
【解答】解:①M连接AB中点E,N连接BC中点F,得到MNFE平行于平面ACC′A′,面面平行即可得到线面平行,故①正确;
②M连接A′C中点G,连接C′G,A′C⊥平面MNC′G.∴MN⊥A′C,故②正确;
③三棱锥N﹣A′BC的体积为= S△BCA′ MB′= CA′ BC MB′=,故③正确;
④由三视图可知:此多面体是正方体切割下来了的,M是A′B的中点(空间对角线中点),是正方体中心,∴点M是该多面体外接球的球心.故④正确.
∴正确的是①②③④.
故答案为:①②③④.
三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)
17.已知直线l1:x+my+1=0和l2:(m﹣3)x﹣2y+(13﹣7m)=0.
(1)若l1⊥l2,求实数m的值;
(2)若l1∥l2,求l1与l2之间的距离d.
【考点】两条平行直线间的距离;直线的一般式方程与直线的垂直关系.
【分析】(1)由垂直可得1 (m﹣3)﹣2m=0,解方程可得;
(2)由l1∥l2可得m值,可得直线方程,由平行线间的距离公式可得.
【解答】解:(1)∵直线l1:x+my+1=0和l2:(m﹣3)x﹣2y+(13﹣7m)=0,
∴当l1⊥l2时,1 (m﹣3)﹣2m=0,解得m=﹣3;
(2)由l1∥l2可得m(m﹣3)+2=0,解得m=1或m=﹣2,
当m=2时,l1与l2重合,应舍去,
当m=1时,可得l1:x+y+1=0,l2:﹣2x﹣2y+6=0,即x+y﹣3=0,
由平行线间的距离公式可得d==2
18.已知函数f(x)=lg(x2﹣x﹣2)的定义域为集合A,函数,x∈[0,9]的值域为集合B,
(1)求A∩B;
(2)若C={x|3x<2m﹣1},且(A∩B) C,求实数m的取值范围.
【考点】集合的包含关系判断及应用;交集及其运算.
【分析】(1)由对数函数的定义域求出集合A,由函数,x∈[0,9]的值域求出集合B,则A∩B可求;
(2)由集合C化为且(A∩B) C得到不等式,求解不等式即可得到实数m的取值范围.
【解答】解:(1)已知函数f(x)=lg(x2﹣x﹣2)的定义域为集合A,函数,x∈[0,9]的值域为集合B,
则A={x|x2﹣x﹣2>0}={x|x<﹣1或x>2},B={x|0≤x≤3},
∴A∩B={x|x<﹣1或x>2}∩{x|0≤x≤3}={x|2<x≤3};
(2)∵且(A∩B) C,
∴,即m>5.
19.如图,△PAD与正方形ABCD共用一边AD,平面PAD⊥平面ABCD,其中PA=PD,AB=2,点E是棱PA的中点.
(1)求证:PC∥平面BDE;
(2)若直线PA与平面ABCD所成角为60°,求点A到平面BDE的距离.
【考点】点、线、面间的距离计算;直线与平面平行的判定.
【分析】(1)连接AC,交BD于O,连接EO,证明PC∥OE,即可证明PC∥平面BDE;
(2)取AD的中点N,连接PN,证明∠PAN为直线PA与平面ABCD所成角,利用等体积方法求点A到平面BDE的距离.
【解答】(1)证明:连接AC,交BD于O,连接EO,则
∵ABCD是正方形,
∴O是AC的中点,
∵点E是棱PA的中点,
∴PC∥OE,
∵OE 平面BDE,BD 平面BDE,
∴PC∥平面BDE;
(2)解:取AD的中点N,连接PN,则
∵PA=PD,
∴PN⊥AD,
∵平面PAD∩平面ABCD=AD,
∴PN⊥平面ABCD,
∴∠PAN为直线PA与平面ABCD所成角∴∠PAN=60°∴PA=PD=AD=2,
∵AB⊥AD,平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,
∴AB⊥平面PAD,
∴VB﹣DAE==,
Rt△EAB中,EA=1,AB=2,BE=,
∵,BD=2,
∴DE⊥EB,
∴S△BDE==.
设点A到平面BDE的距离为h.则,
∴h=,
∴点A到平面BDE的距离为.
20.已知函数.
(1)判断f(x)的奇偶性;
(2)当x∈[﹣1,1]时,f(x)≥m恒成立,求m的取值范围.
【考点】函数恒成立问题;函数奇偶性的判断.
【分析】(1)根据函数奇偶性的定义判断即可;(2)根据函数单调性的定义判断其单调性,从而求出函数的最小值,求出m的范围.
【解答】解:(1)在函数f(x)的定义域R上任取一自变量x
因为=﹣f(x),
所以函数f(x)为奇函数;┅
(2)当a>1时,在[﹣1,1]上任取x1,x2,令x1<x2,
=,
∵0≤x1<x2≤1,
∴f(x1)﹣f(x2)<0
所以函数f(x)在x∈[﹣1,1]时为增函数,┅
当0<a<1时,同理可证函数f(x)在x∈[﹣1,1]时为增函数,
,
所以m≤1┅
21.已知点A(6,2),B(3,2),动点M满足|MA|=2|MB|.
(1)求点M的轨迹方程;
(2)设M的轨迹与y轴的交点为P,过P作斜率为k的直线l与M的轨迹交于另一点Q,若C(1,2k+2),求△CPQ面积的最大值,并求出此时直线l的方程.
【考点】直线与圆锥曲线的综合问题;轨迹方程.
【分析】(1)设M(x,y),由|MA|=2|MB|,利用两点之间的距离公式即可得出.
(2)令x=0,可得P(0,2).直线l的方程为:y=kx+2,(k≠0)代入圆的方程可得:(1+k2)x2﹣4x=0,解出可得Q坐标,|PQ|.求出点C到直线l的距离d,△CPQ面积S=|PQ| d,再利用基本不等式的性质即可得出.
【解答】解:(1)设M(x,y),∵|MA|=2|MB|,
∴=2,
化为:(x﹣2)2+(y﹣2)2=4.
(2)令x=0,解得y=2,∴P(0,2).
直线l的方程为:y=kx+2,(k≠0)代入圆的方程可得:(1+k2)x2﹣4x=0,
解得x=0,或x=.
∴Q.
∴|PQ|==.
点C到直线l的距离d==.
∴△CPQ面积S=|PQ| d=××==≤=1,当且仅当|k|=1时取等号.
∴△CPQ面积的最大值1时,此时直线l的方程为:y=±x+2.
22.已知函数f(x)=ax2+bx+c(a,b,c∈R且a≠0),若对任意实数x,不等式2x≤f(x)(x+1)2恒成立.
(1)求f(1)的值;
(2)求a的取值范围;
(3)若函数g(x)=f(x)+2a|x﹣1|,x∈[﹣2,2]的最小值为﹣1,求a的值.
【考点】二次函数的性质.
【分析】(1)在给出的不等式中,令x=1,根据这个条件可求出f(1)的值;
(2)联立f(1)=2,即可求出a+c与b的关系式.由f(x)﹣2x≥0恒成立,即:ax2+(b﹣1)x+c≥0对于一切实数x恒成立,只有当a>0,且△=(b﹣2)2﹣4ac≤0时,求得a=c>0,再由f(x)(x+1)2恒成立,可得二次项系数小于0,判别式小于等于0,解不等式即可得到a的范围;
(3)讨论当1≤x≤2时,当﹣2≤x<1时,去掉绝对值,运用二次函数的对称轴和区间的关系,求得最小值,解方程可得a的值.
【解答】解:(1)令x=1,由2x≤f(x)(x+1)2可得,
2≤f(1)≤2,∴f(1)=2;
(2)由f(1)=2可得a+b+c=2,即为b=2﹣(a+c),
∵对于一切实数x,f(x)﹣2x≥0恒成立,
∴ax2+(b﹣2)x+c≥0(a≠0)对于一切实数x恒成立,
∴,即.
可得(a﹣c)2≤0,但(a﹣c)2≥0,即有a=c>0,
则f(x)=ax2+bx+a,
f(x)(x+1)2恒成立,即为(a﹣)x2+(b﹣1)x+(a﹣)≤0,
可得a﹣<0,且△=(b﹣1)2﹣4(a﹣)2≤0,
由b﹣1=1﹣2a,即有△=0成立;
综上可得a的范围是(0,);
(3)函数g(x)=f(x)+2a|x﹣1|=ax2+(2﹣2a)x+a+2a|x﹣1|(0<a<),
当1≤x≤2时,g(x)=ax2+2x﹣a在[1,2]递增,可得x=1时,取得最小值2;
当﹣2≤x<1时,g(x)=ax2+(2﹣4a)x+3a,对称轴为x=,
当≤﹣2,即为0<a≤时,[﹣2,1)递增,
可得x=﹣2取得最小值,且为4a﹣4+8a+3a=﹣1,解得a=;
当>﹣2,即<a<时,
x=,取得最小值,且为=﹣1,
解得a= (,).
综上可得,a=.
2016年11月4日
同课章节目录
