12.3 三角形中的主要线段 同步练习(含答案)
文档属性
| 名称 | 12.3 三角形中的主要线段 同步练习(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 163.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-11-04 00:00:00 | ||
图片预览

文档简介
12.3
三角形中的主要线段
基础能力训练
◆对三角形中线的认识
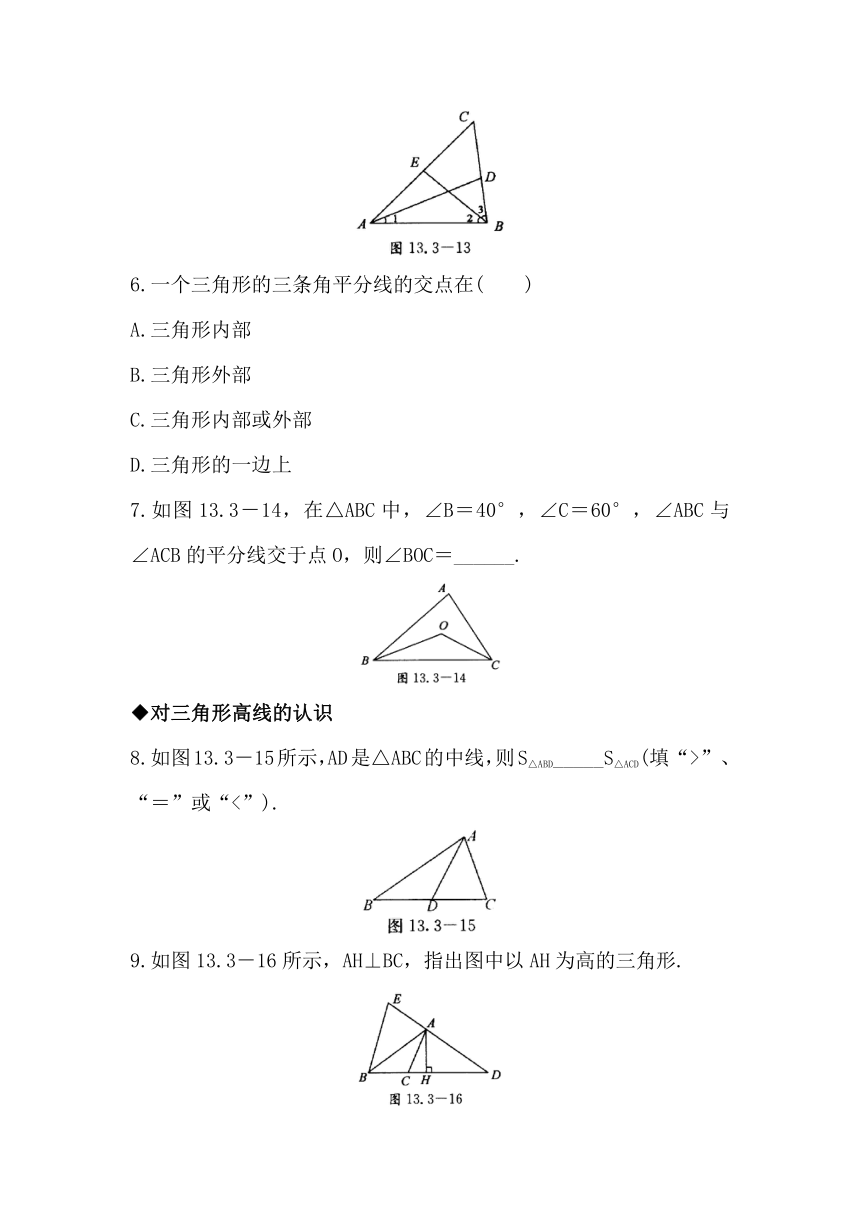
1.如图13.3-9所示,已知AD、BE是△ABC的中线,那么CE=_____;BD=______;
2.如图13.3-10所示,在△ABC中,AD是中线,则△ABD的面积_____△ACD的面积.(填“大于”或“小于”或“等于”).
3.如图13.3-11所示,D、E是边AC的三等分点,BD是△______中AE边上的中线,BE是△_____中DC边上的中线.
4.如图13.3-12所示,在△ABC中,过点A作一条直线与BC相交,将△ABC的面积分为相等的两部分,该直线应该怎样作出
◆对三角形角平分线的认识
5.如图13.3-13,已知∠1=∠BAC,∠2=∠3,则∠BAC的平分线为_______,∠ABC的平分线为______.
6.一个三角形的三条角平分线的交点在(
)
A.三角形内部
B.三角形外部
C.三角形内部或外部
D.三角形的一边上
7.如图13.3-14,在△ABC中,∠B=40°,∠C=60°,∠ABC与∠ACB的平分线交于点O,则∠BOC=______.
◆对三角形高线的认识
8.如图13.3-15所示,AD是△ABC的中线,则S△ABD_____S△ACD(填“>”、“=”或“<”).
9.如图13.3-16所示,AH⊥BC,指出图中以AH为高的三角形.
10.关于三角形的角平分线、中线、高线的说法正确的是(
)
A.都是射线
B.都是线段
C.都是射线或线段
D.都一定位于三角形的内部
综合创新训练
◆综合应用
11.如图13.3-17所示,在△ABC中,∠B=50°,∠C=70°,且AD为△ABC的高,AE为△ABC的角平分线,求∠DAE的度数.
12.如图13.3-18所示,点E、F分别为BC、BD上的点,∠BAF=∠DAF,D为AC的中点.则AF是哪个三角形的角平分线 AE是哪个三角形的角平分线 AC边上的中线是哪条线段
◆生活拓展
13.有一块肥沃的耕地,其中一边与灌渠相邻,如图13.3-19所示,现要将该地按人口分给甲、乙、丙三家.若甲家有6口人,乙家有5口人,丙家有4口人,且每户所得到的土地都和灌渠相邻.请你设计一个合理的分配方案.
参考答案
1答案:AE
CD
解析:根据三角形中线的定义得AE=CE,BD=CD.
2答案:等于
解析:这两个三角形等底同高,所以它们的面积相等.
3答案:ABE
BCD
4答案:解析:作BC边上的中线,三角形的中线把三角形分成两个面积相等的三角形.
5答案:AD
BE
6答案:A
解析:三角形的三条角平分线相交于三角形的内部.
7答案:130°
解析:∠BOC=180°-(∠OBC+∠OCB)=180°-(∠ABC+∠ACB)=180°-(180°-∠A)=180°-50°=130°.
8答案:=
解析:三角形面积等于底与高乘积的一半,由AD是中线得底相等,而高是同一条线段,故填“=”.
9答案:解析:△ABC;△ABD;△ABH;△ADH;△ACD;△ACH.
10答案:B
解析:三角形的角平分线、中线、高线都是线段,并且都相交于一点.
11答案:解析:∵∠B=50°,∠C=70°,∴∠BAC=60°,∵AD为△ABC的高,∴∠CAD=20°,∵AE为△ABC的角平分线,∴∠CAE=∠BAE=30°,∴∠DAE=10°.
12答案:解析:AF是△ABD的角平分线;AE是△ABC的角平分线;AC边上的中线是BD.
13答案:解析:把三角形地块靠近水的边分成15等份,甲有6口人占6份,乙有5口人占5份,丙有4口人占4份,这样得到△AEC、△ADE、△ABD就分别是三家的土地.
三角形中的主要线段
基础能力训练
◆对三角形中线的认识
1.如图13.3-9所示,已知AD、BE是△ABC的中线,那么CE=_____;BD=______;
2.如图13.3-10所示,在△ABC中,AD是中线,则△ABD的面积_____△ACD的面积.(填“大于”或“小于”或“等于”).
3.如图13.3-11所示,D、E是边AC的三等分点,BD是△______中AE边上的中线,BE是△_____中DC边上的中线.
4.如图13.3-12所示,在△ABC中,过点A作一条直线与BC相交,将△ABC的面积分为相等的两部分,该直线应该怎样作出
◆对三角形角平分线的认识
5.如图13.3-13,已知∠1=∠BAC,∠2=∠3,则∠BAC的平分线为_______,∠ABC的平分线为______.
6.一个三角形的三条角平分线的交点在(
)
A.三角形内部
B.三角形外部
C.三角形内部或外部
D.三角形的一边上
7.如图13.3-14,在△ABC中,∠B=40°,∠C=60°,∠ABC与∠ACB的平分线交于点O,则∠BOC=______.
◆对三角形高线的认识
8.如图13.3-15所示,AD是△ABC的中线,则S△ABD_____S△ACD(填“>”、“=”或“<”).
9.如图13.3-16所示,AH⊥BC,指出图中以AH为高的三角形.
10.关于三角形的角平分线、中线、高线的说法正确的是(
)
A.都是射线
B.都是线段
C.都是射线或线段
D.都一定位于三角形的内部
综合创新训练
◆综合应用
11.如图13.3-17所示,在△ABC中,∠B=50°,∠C=70°,且AD为△ABC的高,AE为△ABC的角平分线,求∠DAE的度数.
12.如图13.3-18所示,点E、F分别为BC、BD上的点,∠BAF=∠DAF,D为AC的中点.则AF是哪个三角形的角平分线 AE是哪个三角形的角平分线 AC边上的中线是哪条线段
◆生活拓展
13.有一块肥沃的耕地,其中一边与灌渠相邻,如图13.3-19所示,现要将该地按人口分给甲、乙、丙三家.若甲家有6口人,乙家有5口人,丙家有4口人,且每户所得到的土地都和灌渠相邻.请你设计一个合理的分配方案.
参考答案
1答案:AE
CD
解析:根据三角形中线的定义得AE=CE,BD=CD.
2答案:等于
解析:这两个三角形等底同高,所以它们的面积相等.
3答案:ABE
BCD
4答案:解析:作BC边上的中线,三角形的中线把三角形分成两个面积相等的三角形.
5答案:AD
BE
6答案:A
解析:三角形的三条角平分线相交于三角形的内部.
7答案:130°
解析:∠BOC=180°-(∠OBC+∠OCB)=180°-(∠ABC+∠ACB)=180°-(180°-∠A)=180°-50°=130°.
8答案:=
解析:三角形面积等于底与高乘积的一半,由AD是中线得底相等,而高是同一条线段,故填“=”.
9答案:解析:△ABC;△ABD;△ABH;△ADH;△ACD;△ACH.
10答案:B
解析:三角形的角平分线、中线、高线都是线段,并且都相交于一点.
11答案:解析:∵∠B=50°,∠C=70°,∴∠BAC=60°,∵AD为△ABC的高,∴∠CAD=20°,∵AE为△ABC的角平分线,∴∠CAE=∠BAE=30°,∴∠DAE=10°.
12答案:解析:AF是△ABD的角平分线;AE是△ABC的角平分线;AC边上的中线是BD.
13答案:解析:把三角形地块靠近水的边分成15等份,甲有6口人占6份,乙有5口人占5份,丙有4口人占4份,这样得到△AEC、△ADE、△ABD就分别是三家的土地.
同课章节目录
- 第十章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的乘除法
- 10.4 分式的加减法
- 10.5 可化为一元一次方程的分式方程及其应用
- 第十一章 实数和二次根式
- 11.1 平方根
- 11.2 立方根
- 11.3 用科学计算器开方
- 11.4 无理数与实数
- 11.5 二次根式及其性质
- 11.6 二次根式的乘除法
- 11.7 二次根式的加减法
- 第十二章 三角形
- 12.1 三角形
- 12.2 三角形的性质
- 12.3 三角形中的主要线段
- 12.4 全等三角形
- 12.5 全等三角形的判定
- 12.6 等腰三角形
- 12.7 直角三角形
- 12.8 基本作图
- 12.9 逆命题 、逆定理
- 12.10 轴对称和轴对称图形
- 12.11 勾股定理
- 12.12 勾股定理的逆定理
- 第十三章 事件与可能性
- 13.1 必然事件与随机事件
- 13.2 随机事件发生的可能性
- 13.3 求简单随机事件发生的可能性的大小
