泰安高新区2016-2017学年上学期九年级数学期中考试试题(含答案)
文档属性
| 名称 | 泰安高新区2016-2017学年上学期九年级数学期中考试试题(含答案) | 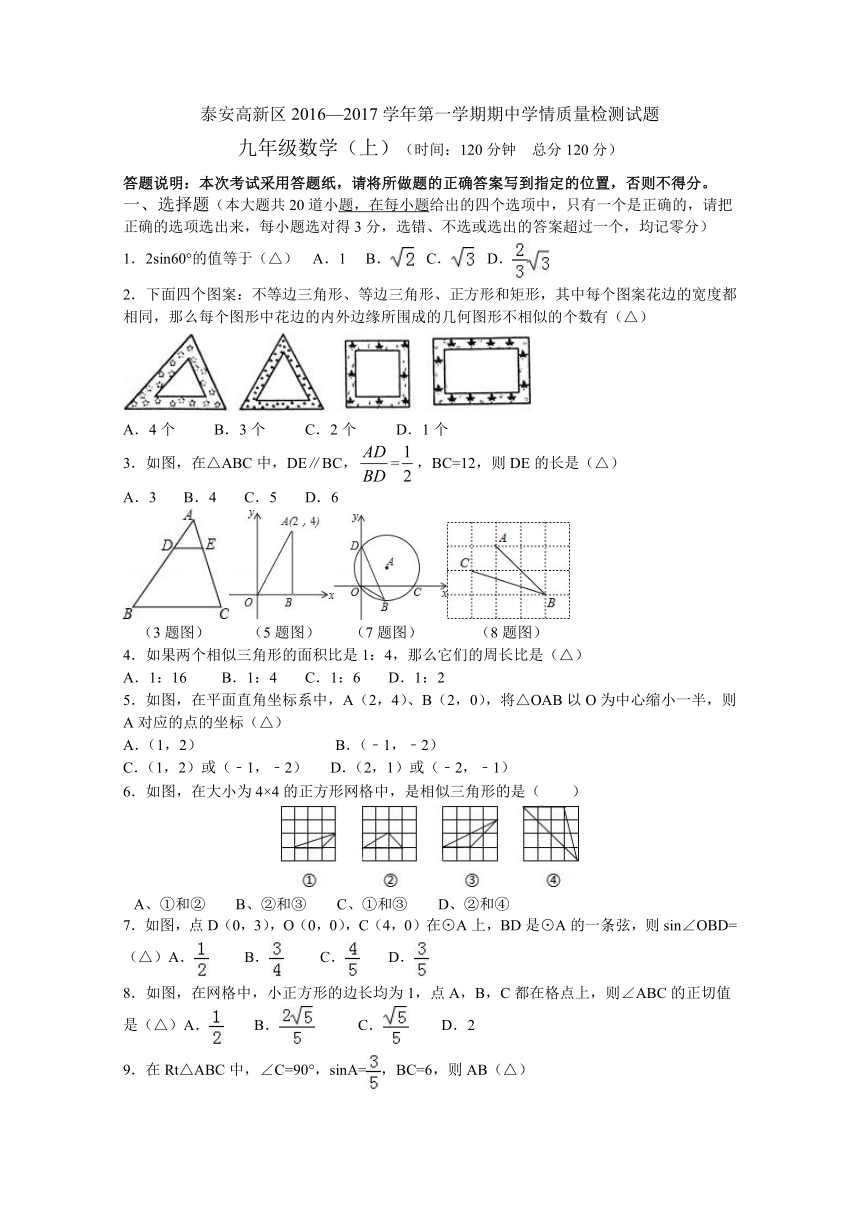 | |
| 格式 | zip | ||
| 文件大小 | 154.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-11-04 18:59:28 | ||
图片预览

文档简介
泰安高新区2016—2017学年第一学期期中学情质量检测试题
九年级数学(上)(时间:120分钟
总分120分)
答题说明:本次考试采用答题纸,请将所做题的正确答案写到指定的位置,否则不得分。
一、选择题(本大题共20道小题,在每小题
( http: / / www.21cnjy.com )给出的四个选项中,只有一个是正确的,请把正确的选项选出来,每小题选对得3分,选错、不选或选出的答案超过一个,均记零分)
1.2sin60°的值等于(△)
A.1
B.
C.
D.
2.下面四个图案:不等边三角形、等边三角形、正方形和矩形,其中每个图案花边的宽度都相同,那么每个图形中花边的内外边缘所围成的几何图形不相似的个数有(△)
( http: / / www.21cnjy.com )
A.4个
B.3个
C.2个
D.1个
3.如图,在△ABC中,DE∥BC,=,BC=12,则DE的长是(△)
A.3
B.4
C.5
D.6
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
(3题图)
(5题图)
(7题图)
(8题图)
4.如果两个相似三角形的面积比是1:4,那么它们的周长比是(△)
A.1:16
B.1:4
C.1:6
D.1:2
5.如图,在平面直角坐标系中,A(2,4)、B(2,0),将△OAB以O为中心缩小一半,则A对应的点的坐标(△)
A.(1,2)
B.(﹣1,﹣2)
C.(1,2)或(﹣1,﹣2)
D.(2,1)或(﹣2,﹣1)
6.如图,在大小为4×4的正方形网格中,是相似三角形的是( )
( http: / / www.21cnjy.com )
A、①和②
B、②和③
C、①和③
D、②和④
7.如图,点D(0,3),O(0,0),C(4,0)在⊙A上,BD是⊙A的一条弦,则sin∠OBD=(△)A.
B.
C.
D.
8.如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正切值是(△)A.
B.
C.
D.2
9.在Rt△ABC中,∠C=90°,sinA=,BC=6,则AB(△)
A.4
B.6
C.8
D.10
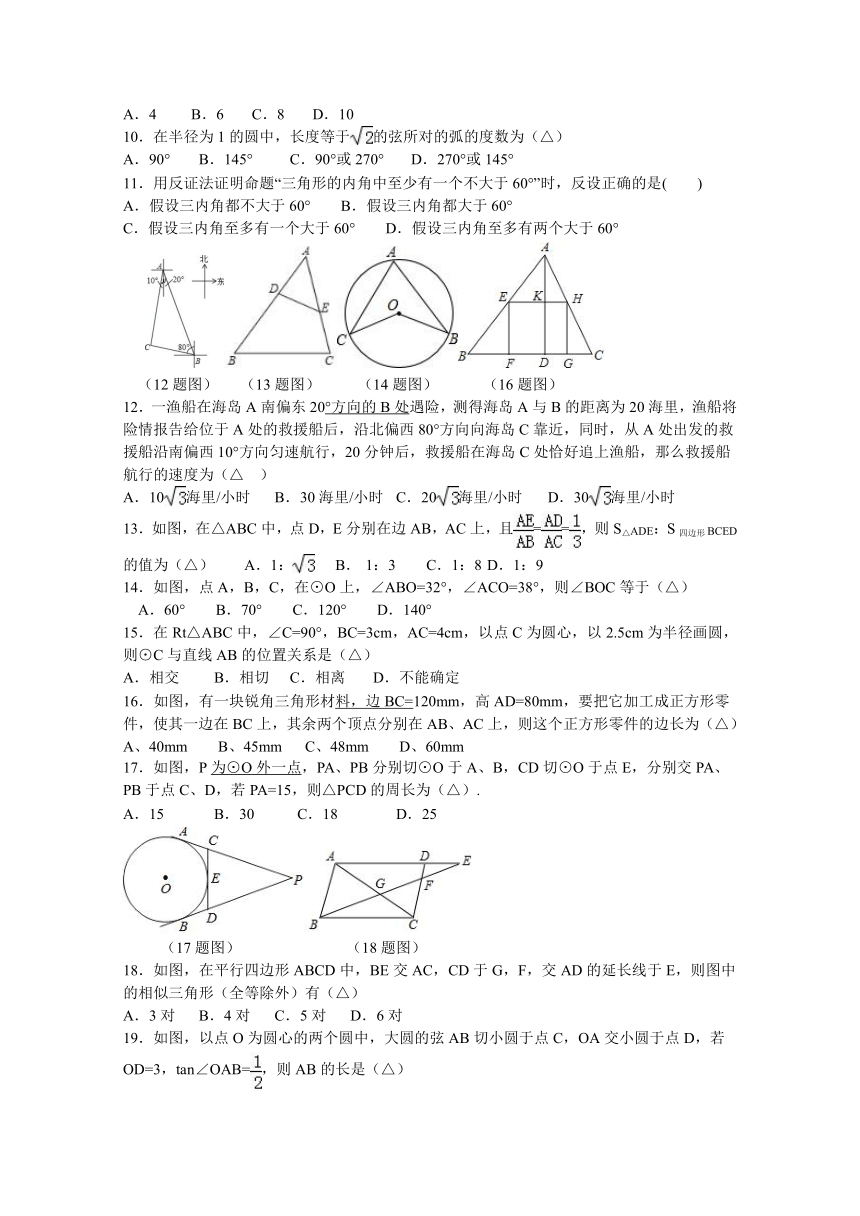
10.在半径为1的圆中,长度等于的弦所对的弧的度数为(△)
A.90°
B.145°
C.90°或270°
D.270°或145°
11.用反证法证明命题“三角形的内角中至少有一个不大于60°”时,反设正确的是( )
A.假设三内角都不大于60°
B.假设三内角都大于60°
C.假设三内角至多有一个大于60°
D.假设三内角至多有两个大于60°
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
(12题图)
(13题图)
(14题图)
(16题图)
12.一渔船在海岛A南偏东20°方向的B处
( http: / / www.21cnjy.com )遇险,测得海岛A与B的距离为20海里,渔船将险情报告给位于A处的救援船后,沿北偏西80°方向向海岛C靠近,同时,从A处出发的救援船沿南偏西10°方向匀速航行,20分钟后,救援船在海岛C处恰好追上渔船,那么救援船航行的速度为(△ )
A.10海里/小时
B.30海里/小时
C.20海里/小时
D.30海里/小时
13.如图,在△ABC中,点D,E分别在边AB,AC上,且==,则S△ADE:S四边形BCED的值为(△)
A.1:
B.
1:3
C.1:8
D.1:9
14.如图,点A,B,C,在⊙O上,∠ABO=32°,∠ACO=38°,则∠BOC等于(△)
A.60°
B.70°
C.120°
D.140°
15.在Rt△ABC中,∠C=90°,BC=3cm,AC=4cm,以点C为圆心,以2.5cm为半径画圆,则⊙C与直线AB的位置关系是(△)
A.相交
B.相切
C.相离
D.不能确定
16.如图,有一块锐角三角形材料,边BC=
( http: / / www.21cnjy.com )120mm,高AD=80mm,要把它加工成正方形零件,使其一边在BC上,其余两个顶点分别在AB、AC上,则这个正方形零件的边长为(△)
A、40mm
B、45mm
C、48mm
D、60mm
17.如图,P为⊙O外一点
( http: / / www.21cnjy.com ),PA、PB分别切⊙O于A、B,CD切⊙O于点E,分别交PA、PB于点C、D,若PA=15,则△PCD的周长为(△).
A.15
B.30
C.18
D.25
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
(17题图)
(18题图)
18.如图,在平行四边形ABCD中,BE交AC,CD于G,F,交AD的延长线于E,则图中的相似三角形(全等除外)有(△)
A.3对
B.4对
C.5对
D.6对
19.如图,以点O为圆心的两个圆中,大圆的弦AB切小圆于点C,OA交小圆于点D,若OD=3,tan∠OAB=,则AB的长是(△)
A.12
B.6
C.8
D.3
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
(19题图)
(20题图)
(21题图)
(23题图)
20.如图,在半径为2,圆心角为90°的扇形内,以BC为直径作半圆,交弦AB于点D,连接CD,则阴影部分的面积为(△)
A.π﹣1
B.2π﹣1
C.π﹣1
D.π﹣2
二.填空题(每小题3分,共计12分。)
21.如图所示,已知点E在AC上,若点D在AB上,则满足条件
△
(只填一个条件),使△ADE与原△ABC相似.
22.已知三角形的三边分别是5、12、13,则其内切圆的直径与外接圆的直径之比是
△
。
23.如图,AB是⊙O的直径,且经过弦CD的中点H,过CD延长线上一点E作⊙O的切线,切点为F.若∠ACF=65°,则∠E=
△
.
24.在矩形ABCD中,已知AB=4,
( http: / / www.21cnjy.com )BC=3,矩形在直线l上绕其右下角的顶点B向右旋转90°至图①位置,再绕右下角的顶点继续向右旋转90°至图②位置,…,以此类推,这样连续旋转2016次后,顶点A在整个旋转过程中所经过的路程之和是
△
。
三.解答题(共5小题,满分48分。写出必要的文字说明或推演步骤)
25.(10分)如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,
(1)求证:AC2=AB AD;(2)求证:CE∥AD;(3)若AD=5,AB=8,求的值.
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
(25题图)
(26题图)
(27题图)
(28题图)
26.(8分)如图,山坡AB的坡度i=1:,AB=10米,AE=15米.在高楼的顶端竖立一块倒计时牌CD,在点B处测量计时牌的顶端C的仰角是45°,在点A处测量计时牌的底端D的仰角是60°,求这块倒计时牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米,参考数据:≈1.414,≈1.732)
27.(8分)如图,AB是⊙O的直径,C是的中点,CE⊥AB于E,BD交CE于点F,
(1)求证:CF=BF;
(2)若CD=12,AC=16,求⊙O的半径和CE的长.
28.(10分)如图,Rt△ABC中,∠ABC=90°,以AB为直径作半圆⊙O交AC与点D,点E为BC的中点,连接DE.
(1)求证:DE是半圆⊙O的切线.
(2)若∠BAC=30°,DE=2,求AD的长.
29.(12分)如图1,将菱形纸片
( http: / / www.21cnjy.com )AB(E)CD(F)沿对角线BD(EF)剪开,得到△ABD和△ECF,固定△ABD,并把△ABD与△ECF叠放在一起.
( http: / / www.21cnjy.com )
(1)操作:如图2,将△ECF的顶
( http: / / www.21cnjy.com )点F固定在△ABD的BD边上的中点处,△ECF绕点F在BD边上方左右旋转,设旋转时FC交BA于点H(H点不与B点重合),FE交DA于点G(G点不与D点重合).
求证:BH GD=BF2
(2)操作:如图3,△ECF的顶点F在△AB
( http: / / www.21cnjy.com )D的BD边上滑动(F点不与B、D点重合),且CF始终经过点A,过点A作AG∥CE,交FE于点G,连接DG.
探究:FD+DG= .请予证明.
九年级数学(上)参考答案
一、选择题(每小题3分,共计60分)
1.C.2.D.3.B.4.D.5.C.6.C.7.D.8.A.9.D
10.C.11.B.
12.D.13.C.14.D.15.A.16.C.17.B.18.C.19.A.20.A.
二.填空题(每小题3分,共计12分)
21. ∠B=∠AED或∠C=∠ADE或AE:AB=AD:AC 22.4:13
23.50°.24.3024π
。
三、解答题写出必要的文字说明或推演步骤
25.(10分)(1)证明:∵AC平分∠DAB,∴∠DAC=∠CAB,
∵∠ADC=∠ACB=90°,∴△ADC∽△ACB,
∴AD:AC=AC:AB,∴AC2=AB AD;
…………………4分
(2)证明:∵E为AB的中点,∴CE=AB=AE,∴∠EAC=∠ECA,
∵∠DAC=∠CAB,∴∠DAC=∠ECA,∴CE∥AD;
………………7分
(3)解:∵CE∥AD,∴△AFD∽△CFE,∴AD:CE=AF:CF,
∵CE=AB,∴CE=×8=4,
∵AD=5,∴,∴.
………………10分
26.(8分)解:作BF⊥DE于点F,BG⊥AE于点G,
∵CE⊥AE,∴四边形BGEF为矩形,∴BG=EF,BF=GE,
在Rt△ADE中,∵tan∠ADE=,∴DE=AE tan∠ADE=15,………………4分
∵山坡AB的坡度i=1:,AB=10,∴BG=5,AG=5,
∴EF=BG=5,BF=AG+AE=5+15,
…………………6分
∵∠CBF=45°∴CF=BF=5+15,
∴CD=CF+EF﹣DE=20﹣10≈20﹣10×1.732=2.68≈2.7(m),
答:这块宣传牌CD的高度为2.7米.
…………………8分
27、(8分)解:(1)证明:∵AB是⊙O的直径,∴∠ACB=90°,
又∵CE⊥AB,∴∠CEB=90°,∴∠2=90°﹣∠ABC=∠A,
又∵C是弧BD的中点,∴∠1=∠A,∴∠1=∠2,∴CF=BF;…………………4分
(2)∵C是弧BD的中点,∴=,∴BC=CD=12,
又∵在Rt△ABC中,AC=16,∴由勾股定理可得:AB=20,∴⊙O的半径为10,
∵S△ABC=AC BC=AB CE,∴CE==9.6.
……………………8分
28.(10分)(1)证明:连接OD,OE,∵AB为圆O的直径,∴∠ADB=∠BDC=90°,
在Rt△BDC中,E为斜边BC的中点,∴DE=BE,
在△OBE和△ODE中,,∴△OBE≌△ODE(SSS),∴∠ODE=∠ABC=90°,
则DE为圆O的切线;
…………………………………6分
(2)在Rt△ABC中,∠BAC=30°,∴BC=AC,∵BC=2DE=4,∴AC=8,
又∵∠C=60°,DE=CE,
∴△DEC为等边三角形,即DC=DE=2,则AD=AC﹣DC=6.……………………10分
29.答案为:BD(或EF).
………………………………2分
证明:(1)∵将菱形纸片AB(E)CD(F)沿对角线BD(EF)剪开,∴∠B=∠D,
∵将△ECF的顶点F固定在
( http: / / www.21cnjy.com )△ABD的BD边上的中点处,△ECF绕点F在BD边上方左右旋转,∴BF=DF,
………………………………4分
∵∠HFG=∠B,又∵∠
( http: / / www.21cnjy.com )HFD=∠HFG+∠GFD=∠B+∠BHF,∴∠GFD=∠BHF,∴△BFH∽△DGF,
………………………………6分
∴,∴BH GD=BF2;
………………………………8分
(2)∵AG∥CE,∴∠FAG=∠C,
∵∠CFE=∠CEF,∴∠AGF=∠CFE,∴AF=AG,
……………………10分
∵∠BAD=∠C,∴∠BAF=∠DAG,
又∵AB=AD,∴△ABF≌△ADG,
∴FB=DG,∴FD+DG=BD,
……………………12分
九年级数学(上)(时间:120分钟
总分120分)
答题说明:本次考试采用答题纸,请将所做题的正确答案写到指定的位置,否则不得分。
一、选择题(本大题共20道小题,在每小题
( http: / / www.21cnjy.com )给出的四个选项中,只有一个是正确的,请把正确的选项选出来,每小题选对得3分,选错、不选或选出的答案超过一个,均记零分)
1.2sin60°的值等于(△)
A.1
B.
C.
D.
2.下面四个图案:不等边三角形、等边三角形、正方形和矩形,其中每个图案花边的宽度都相同,那么每个图形中花边的内外边缘所围成的几何图形不相似的个数有(△)
( http: / / www.21cnjy.com )
A.4个
B.3个
C.2个
D.1个
3.如图,在△ABC中,DE∥BC,=,BC=12,则DE的长是(△)
A.3
B.4
C.5
D.6
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
(3题图)
(5题图)
(7题图)
(8题图)
4.如果两个相似三角形的面积比是1:4,那么它们的周长比是(△)
A.1:16
B.1:4
C.1:6
D.1:2
5.如图,在平面直角坐标系中,A(2,4)、B(2,0),将△OAB以O为中心缩小一半,则A对应的点的坐标(△)
A.(1,2)
B.(﹣1,﹣2)
C.(1,2)或(﹣1,﹣2)
D.(2,1)或(﹣2,﹣1)
6.如图,在大小为4×4的正方形网格中,是相似三角形的是( )
( http: / / www.21cnjy.com )
A、①和②
B、②和③
C、①和③
D、②和④
7.如图,点D(0,3),O(0,0),C(4,0)在⊙A上,BD是⊙A的一条弦,则sin∠OBD=(△)A.
B.
C.
D.
8.如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正切值是(△)A.
B.
C.
D.2
9.在Rt△ABC中,∠C=90°,sinA=,BC=6,则AB(△)
A.4
B.6
C.8
D.10
10.在半径为1的圆中,长度等于的弦所对的弧的度数为(△)
A.90°
B.145°
C.90°或270°
D.270°或145°
11.用反证法证明命题“三角形的内角中至少有一个不大于60°”时,反设正确的是( )
A.假设三内角都不大于60°
B.假设三内角都大于60°
C.假设三内角至多有一个大于60°
D.假设三内角至多有两个大于60°
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
(12题图)
(13题图)
(14题图)
(16题图)
12.一渔船在海岛A南偏东20°方向的B处
( http: / / www.21cnjy.com )遇险,测得海岛A与B的距离为20海里,渔船将险情报告给位于A处的救援船后,沿北偏西80°方向向海岛C靠近,同时,从A处出发的救援船沿南偏西10°方向匀速航行,20分钟后,救援船在海岛C处恰好追上渔船,那么救援船航行的速度为(△ )
A.10海里/小时
B.30海里/小时
C.20海里/小时
D.30海里/小时
13.如图,在△ABC中,点D,E分别在边AB,AC上,且==,则S△ADE:S四边形BCED的值为(△)
A.1:
B.
1:3
C.1:8
D.1:9
14.如图,点A,B,C,在⊙O上,∠ABO=32°,∠ACO=38°,则∠BOC等于(△)
A.60°
B.70°
C.120°
D.140°
15.在Rt△ABC中,∠C=90°,BC=3cm,AC=4cm,以点C为圆心,以2.5cm为半径画圆,则⊙C与直线AB的位置关系是(△)
A.相交
B.相切
C.相离
D.不能确定
16.如图,有一块锐角三角形材料,边BC=
( http: / / www.21cnjy.com )120mm,高AD=80mm,要把它加工成正方形零件,使其一边在BC上,其余两个顶点分别在AB、AC上,则这个正方形零件的边长为(△)
A、40mm
B、45mm
C、48mm
D、60mm
17.如图,P为⊙O外一点
( http: / / www.21cnjy.com ),PA、PB分别切⊙O于A、B,CD切⊙O于点E,分别交PA、PB于点C、D,若PA=15,则△PCD的周长为(△).
A.15
B.30
C.18
D.25
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
(17题图)
(18题图)
18.如图,在平行四边形ABCD中,BE交AC,CD于G,F,交AD的延长线于E,则图中的相似三角形(全等除外)有(△)
A.3对
B.4对
C.5对
D.6对
19.如图,以点O为圆心的两个圆中,大圆的弦AB切小圆于点C,OA交小圆于点D,若OD=3,tan∠OAB=,则AB的长是(△)
A.12
B.6
C.8
D.3
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
(19题图)
(20题图)
(21题图)
(23题图)
20.如图,在半径为2,圆心角为90°的扇形内,以BC为直径作半圆,交弦AB于点D,连接CD,则阴影部分的面积为(△)
A.π﹣1
B.2π﹣1
C.π﹣1
D.π﹣2
二.填空题(每小题3分,共计12分。)
21.如图所示,已知点E在AC上,若点D在AB上,则满足条件
△
(只填一个条件),使△ADE与原△ABC相似.
22.已知三角形的三边分别是5、12、13,则其内切圆的直径与外接圆的直径之比是
△
。
23.如图,AB是⊙O的直径,且经过弦CD的中点H,过CD延长线上一点E作⊙O的切线,切点为F.若∠ACF=65°,则∠E=
△
.
24.在矩形ABCD中,已知AB=4,
( http: / / www.21cnjy.com )BC=3,矩形在直线l上绕其右下角的顶点B向右旋转90°至图①位置,再绕右下角的顶点继续向右旋转90°至图②位置,…,以此类推,这样连续旋转2016次后,顶点A在整个旋转过程中所经过的路程之和是
△
。
三.解答题(共5小题,满分48分。写出必要的文字说明或推演步骤)
25.(10分)如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,
(1)求证:AC2=AB AD;(2)求证:CE∥AD;(3)若AD=5,AB=8,求的值.
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
(25题图)
(26题图)
(27题图)
(28题图)
26.(8分)如图,山坡AB的坡度i=1:,AB=10米,AE=15米.在高楼的顶端竖立一块倒计时牌CD,在点B处测量计时牌的顶端C的仰角是45°,在点A处测量计时牌的底端D的仰角是60°,求这块倒计时牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米,参考数据:≈1.414,≈1.732)
27.(8分)如图,AB是⊙O的直径,C是的中点,CE⊥AB于E,BD交CE于点F,
(1)求证:CF=BF;
(2)若CD=12,AC=16,求⊙O的半径和CE的长.
28.(10分)如图,Rt△ABC中,∠ABC=90°,以AB为直径作半圆⊙O交AC与点D,点E为BC的中点,连接DE.
(1)求证:DE是半圆⊙O的切线.
(2)若∠BAC=30°,DE=2,求AD的长.
29.(12分)如图1,将菱形纸片
( http: / / www.21cnjy.com )AB(E)CD(F)沿对角线BD(EF)剪开,得到△ABD和△ECF,固定△ABD,并把△ABD与△ECF叠放在一起.
( http: / / www.21cnjy.com )
(1)操作:如图2,将△ECF的顶
( http: / / www.21cnjy.com )点F固定在△ABD的BD边上的中点处,△ECF绕点F在BD边上方左右旋转,设旋转时FC交BA于点H(H点不与B点重合),FE交DA于点G(G点不与D点重合).
求证:BH GD=BF2
(2)操作:如图3,△ECF的顶点F在△AB
( http: / / www.21cnjy.com )D的BD边上滑动(F点不与B、D点重合),且CF始终经过点A,过点A作AG∥CE,交FE于点G,连接DG.
探究:FD+DG= .请予证明.
九年级数学(上)参考答案
一、选择题(每小题3分,共计60分)
1.C.2.D.3.B.4.D.5.C.6.C.7.D.8.A.9.D
10.C.11.B.
12.D.13.C.14.D.15.A.16.C.17.B.18.C.19.A.20.A.
二.填空题(每小题3分,共计12分)
21. ∠B=∠AED或∠C=∠ADE或AE:AB=AD:AC 22.4:13
23.50°.24.3024π
。
三、解答题写出必要的文字说明或推演步骤
25.(10分)(1)证明:∵AC平分∠DAB,∴∠DAC=∠CAB,
∵∠ADC=∠ACB=90°,∴△ADC∽△ACB,
∴AD:AC=AC:AB,∴AC2=AB AD;
…………………4分
(2)证明:∵E为AB的中点,∴CE=AB=AE,∴∠EAC=∠ECA,
∵∠DAC=∠CAB,∴∠DAC=∠ECA,∴CE∥AD;
………………7分
(3)解:∵CE∥AD,∴△AFD∽△CFE,∴AD:CE=AF:CF,
∵CE=AB,∴CE=×8=4,
∵AD=5,∴,∴.
………………10分
26.(8分)解:作BF⊥DE于点F,BG⊥AE于点G,
∵CE⊥AE,∴四边形BGEF为矩形,∴BG=EF,BF=GE,
在Rt△ADE中,∵tan∠ADE=,∴DE=AE tan∠ADE=15,………………4分
∵山坡AB的坡度i=1:,AB=10,∴BG=5,AG=5,
∴EF=BG=5,BF=AG+AE=5+15,
…………………6分
∵∠CBF=45°∴CF=BF=5+15,
∴CD=CF+EF﹣DE=20﹣10≈20﹣10×1.732=2.68≈2.7(m),
答:这块宣传牌CD的高度为2.7米.
…………………8分
27、(8分)解:(1)证明:∵AB是⊙O的直径,∴∠ACB=90°,
又∵CE⊥AB,∴∠CEB=90°,∴∠2=90°﹣∠ABC=∠A,
又∵C是弧BD的中点,∴∠1=∠A,∴∠1=∠2,∴CF=BF;…………………4分
(2)∵C是弧BD的中点,∴=,∴BC=CD=12,
又∵在Rt△ABC中,AC=16,∴由勾股定理可得:AB=20,∴⊙O的半径为10,
∵S△ABC=AC BC=AB CE,∴CE==9.6.
……………………8分
28.(10分)(1)证明:连接OD,OE,∵AB为圆O的直径,∴∠ADB=∠BDC=90°,
在Rt△BDC中,E为斜边BC的中点,∴DE=BE,
在△OBE和△ODE中,,∴△OBE≌△ODE(SSS),∴∠ODE=∠ABC=90°,
则DE为圆O的切线;
…………………………………6分
(2)在Rt△ABC中,∠BAC=30°,∴BC=AC,∵BC=2DE=4,∴AC=8,
又∵∠C=60°,DE=CE,
∴△DEC为等边三角形,即DC=DE=2,则AD=AC﹣DC=6.……………………10分
29.答案为:BD(或EF).
………………………………2分
证明:(1)∵将菱形纸片AB(E)CD(F)沿对角线BD(EF)剪开,∴∠B=∠D,
∵将△ECF的顶点F固定在
( http: / / www.21cnjy.com )△ABD的BD边上的中点处,△ECF绕点F在BD边上方左右旋转,∴BF=DF,
………………………………4分
∵∠HFG=∠B,又∵∠
( http: / / www.21cnjy.com )HFD=∠HFG+∠GFD=∠B+∠BHF,∴∠GFD=∠BHF,∴△BFH∽△DGF,
………………………………6分
∴,∴BH GD=BF2;
………………………………8分
(2)∵AG∥CE,∴∠FAG=∠C,
∵∠CFE=∠CEF,∴∠AGF=∠CFE,∴AF=AG,
……………………10分
∵∠BAD=∠C,∴∠BAF=∠DAG,
又∵AB=AD,∴△ABF≌△ADG,
∴FB=DG,∴FD+DG=BD,
……………………12分
同课章节目录
