18.2 黄金分割 同步练习(含答案)
文档属性
| 名称 | 18.2 黄金分割 同步练习(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 103.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-11-04 00:00:00 | ||
图片预览

文档简介
18.2
黄金分割
基础能力训练
◆黄金分割的定义
1.已知AB=10
cm,P、Q是线段AB的两个黄金分割点,则PQ=________.
2.已知线段AB=1,点P是线段AB的黄金分割点,则AP=________.
3.已知线段AB=b,C为其黄金分割点,求下列各式的值(AC>BC):
(1)_______;(2)_______;
(3)_______;(4)AC-BC=________.
4.正常人的体温一般是37℃左右,室温太高、太低,人都会感觉不舒服,多少摄氏度比较合适呢 有人研究认为该温度正好是人正常体温的黄金分割点,则这个温度约为________.
5.顶角为36°的等腰三角形被称为黄金三角形,在∠A=36°的△ABC中,AB=AC,BD是∠ABC的角平分线,交AC于D,若AC=4
cm,则BC=___________.
6.若S是线段PQ的黄金分割点,且PS>SQ,则(
)
A.SQ2=PS·PQ
B.PS2=SQ·PQ
C.
D.
7.已知M是线段AB的黄金分割点,且AM>BM.
(1)写出线段AB、AM、BM之间的比例式.
(2)如果AB=12
cm,求AM、BM的长.
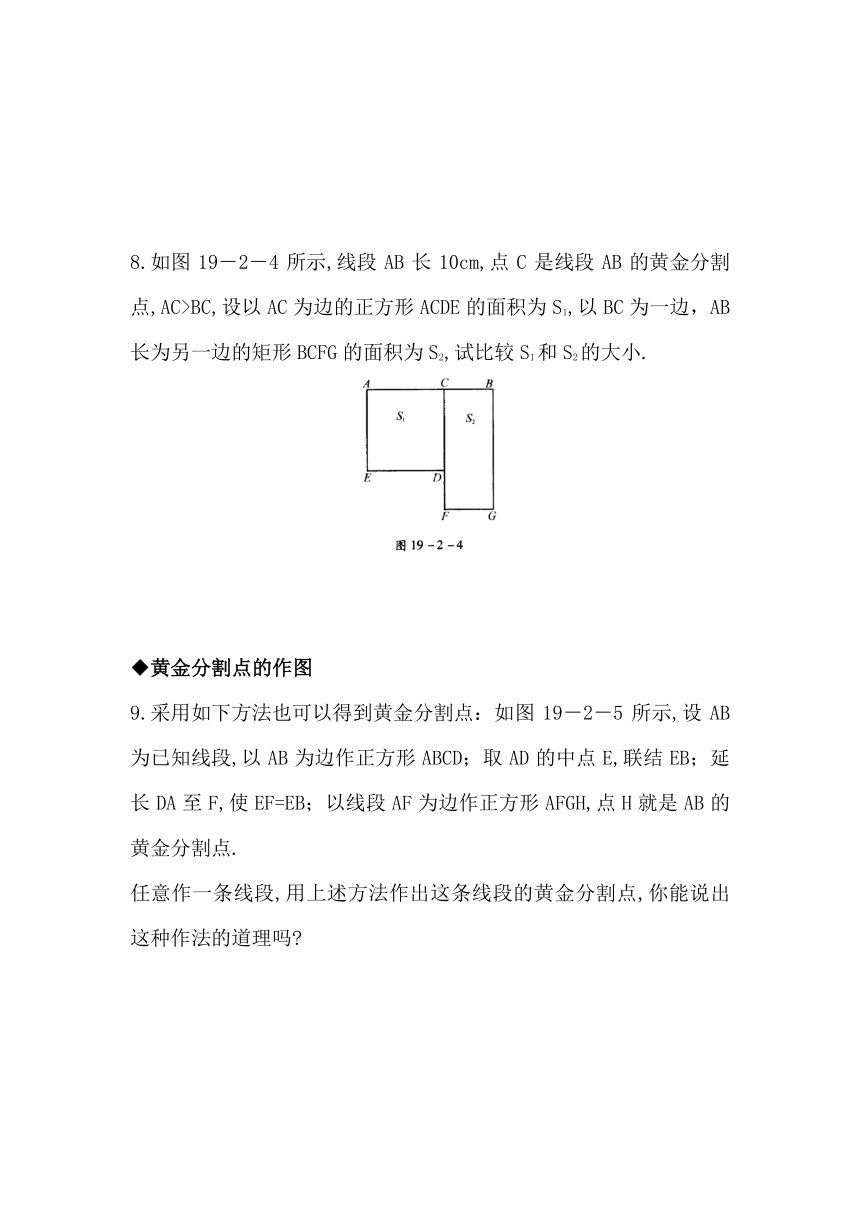
8.如图19-2-4所示,线段AB长10cm,点C是线段AB的黄金分割点,AC>BC,设以AC为边的正方形ACDE的面积为S1,以BC为一边,AB长为另一边的矩形BCFG的面积为S2,试比较S1和S2的大小.
◆黄金分割点的作图
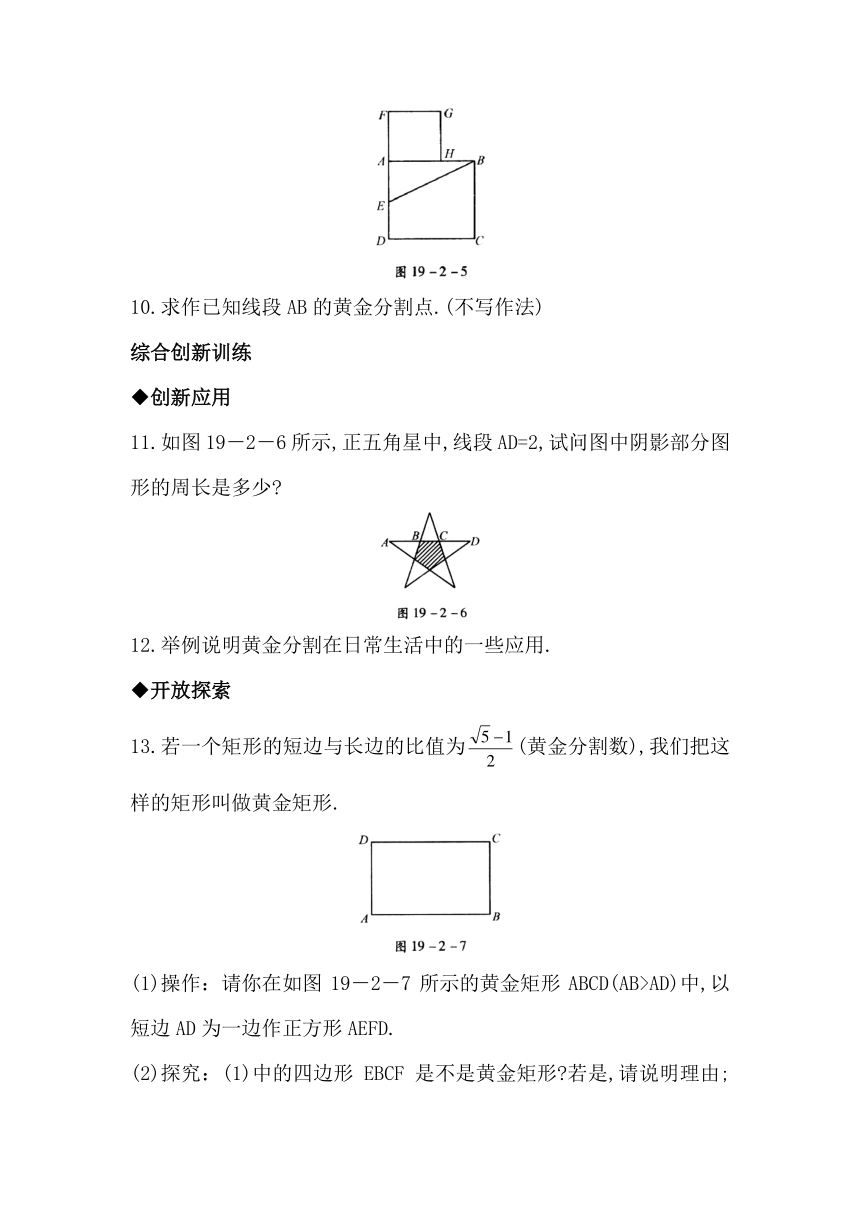
9.采用如下方法也可以得到黄金分割点:如图19-2-5所示,设AB为已知线段,以AB为边作正方形ABCD;取AD的中点E,联结EB;延长DA至F,使EF=EB;以线段AF为边作正方形AFGH,点H就是AB的黄金分割点.
任意作一条线段,用上述方法作出这条线段的黄金分割点,你能说出这种作法的道理吗
10.求作已知线段AB的黄金分割点.(不写作法)
综合创新训练
◆创新应用
11.如图19-2-6所示,正五角星中,线段AD=2,试问图中阴影部分图形的周长是多少
12.举例说明黄金分割在日常生活中的一些应用.
◆开放探索
13.若一个矩形的短边与长边的比值为(黄金分割数),我们把这样的矩形叫做黄金矩形.
(1)操作:请你在如图19-2-7所示的黄金矩形ABCD(AB>AD)中,以短边AD为一边作正方形AEFD.
(2)探究:(1)中的四边形EBCF是不是黄金矩形 若是,请说明理由;若不是,也给予说明.
(3)归纳:通过上述操作及探究,请概括出具有一般性的结沦(不需要证明).
参考答案
1答案:cm
2答案:或
解析:本题应考虑到同一线段上的黄金分割点有两个.
3答案:(1)(2)(3)(4)
4答案:23℃
5答案:cm
解析:∵等腰△ABC为黄金三角形,∴为黄金比.
∴,∴cm.
6答案:B
7答案:(1)
(2)cm,cm
8答案:cm2
9答案:解析:设AB=2,那么在Rt△BAE中,.于是EF=BE=,AH=AF=BE-AE=,BH=AB-AH=.因此,,点H是线段AB的黄金分割点.
10答案:略
11答案:解析:由于点B、C都是线段AD的黄金分割点,于是有:
,
∴.
∴阴影部分的周长为.
12答案:解析:例如:报幕员站在舞台宽度的黄金分割点处,显得最和谐;当矩形的宽与长的比约为0.618时显得美观;拍照时,常把主要景物放在画面的黄金分割点处,会显得更加协调、悦目;二胡中的“千金”分弦的比符合0.618:1时,奏出来的音调最悦耳;优选法中的“0.618法”足黄金分割的重要应用等等.
13答案:解析:(1)如图所示.
(2)四边形EBCF是黄金矩形,因为EF=AE=,,则,所以四边形EBCF是黄金矩形.
(3)在黄金矩形中以短边为边长作一个正方形,另一部分仍为黄金矩形.
黄金分割
基础能力训练
◆黄金分割的定义
1.已知AB=10
cm,P、Q是线段AB的两个黄金分割点,则PQ=________.
2.已知线段AB=1,点P是线段AB的黄金分割点,则AP=________.
3.已知线段AB=b,C为其黄金分割点,求下列各式的值(AC>BC):
(1)_______;(2)_______;
(3)_______;(4)AC-BC=________.
4.正常人的体温一般是37℃左右,室温太高、太低,人都会感觉不舒服,多少摄氏度比较合适呢 有人研究认为该温度正好是人正常体温的黄金分割点,则这个温度约为________.
5.顶角为36°的等腰三角形被称为黄金三角形,在∠A=36°的△ABC中,AB=AC,BD是∠ABC的角平分线,交AC于D,若AC=4
cm,则BC=___________.
6.若S是线段PQ的黄金分割点,且PS>SQ,则(
)
A.SQ2=PS·PQ
B.PS2=SQ·PQ
C.
D.
7.已知M是线段AB的黄金分割点,且AM>BM.
(1)写出线段AB、AM、BM之间的比例式.
(2)如果AB=12
cm,求AM、BM的长.
8.如图19-2-4所示,线段AB长10cm,点C是线段AB的黄金分割点,AC>BC,设以AC为边的正方形ACDE的面积为S1,以BC为一边,AB长为另一边的矩形BCFG的面积为S2,试比较S1和S2的大小.
◆黄金分割点的作图
9.采用如下方法也可以得到黄金分割点:如图19-2-5所示,设AB为已知线段,以AB为边作正方形ABCD;取AD的中点E,联结EB;延长DA至F,使EF=EB;以线段AF为边作正方形AFGH,点H就是AB的黄金分割点.
任意作一条线段,用上述方法作出这条线段的黄金分割点,你能说出这种作法的道理吗
10.求作已知线段AB的黄金分割点.(不写作法)
综合创新训练
◆创新应用
11.如图19-2-6所示,正五角星中,线段AD=2,试问图中阴影部分图形的周长是多少
12.举例说明黄金分割在日常生活中的一些应用.
◆开放探索
13.若一个矩形的短边与长边的比值为(黄金分割数),我们把这样的矩形叫做黄金矩形.
(1)操作:请你在如图19-2-7所示的黄金矩形ABCD(AB>AD)中,以短边AD为一边作正方形AEFD.
(2)探究:(1)中的四边形EBCF是不是黄金矩形 若是,请说明理由;若不是,也给予说明.
(3)归纳:通过上述操作及探究,请概括出具有一般性的结沦(不需要证明).
参考答案
1答案:cm
2答案:或
解析:本题应考虑到同一线段上的黄金分割点有两个.
3答案:(1)(2)(3)(4)
4答案:23℃
5答案:cm
解析:∵等腰△ABC为黄金三角形,∴为黄金比.
∴,∴cm.
6答案:B
7答案:(1)
(2)cm,cm
8答案:cm2
9答案:解析:设AB=2,那么在Rt△BAE中,.于是EF=BE=,AH=AF=BE-AE=,BH=AB-AH=.因此,,点H是线段AB的黄金分割点.
10答案:略
11答案:解析:由于点B、C都是线段AD的黄金分割点,于是有:
,
∴.
∴阴影部分的周长为.
12答案:解析:例如:报幕员站在舞台宽度的黄金分割点处,显得最和谐;当矩形的宽与长的比约为0.618时显得美观;拍照时,常把主要景物放在画面的黄金分割点处,会显得更加协调、悦目;二胡中的“千金”分弦的比符合0.618:1时,奏出来的音调最悦耳;优选法中的“0.618法”足黄金分割的重要应用等等.
13答案:解析:(1)如图所示.
(2)四边形EBCF是黄金矩形,因为EF=AE=,,则,所以四边形EBCF是黄金矩形.
(3)在黄金矩形中以短边为边长作一个正方形,另一部分仍为黄金矩形.
同课章节目录
- 第十八章 相似形
- 18.1 比例线段
- 18.2 黄金分割
- 18.3 平行线分三角形两边成比例
- 18.4 相似多边形
- 18.5 相似三角形的判定
- 18.6 相似三角形的性质
- 18.7 应用举例
- 第十九章 二次函数和反比例函数
- 19.1 二次函数
- 19.2 二次函数 y=ax2+bx+c(a≠0) 的图象
- 19.3 二次函数的性质
- 19.4 二次函数的应用
- 19.5 反比例函数
- 19.6 反比例函数的图象、性质和应用
- 第二十章 解直角三角形
- 20.1 锐角三角函数
- 20.2 30°、45°、60° 角的三角函数值
- 20.3 用科学计算器求锐角三角函数值
- 20.4 解直角三角形
- 20.5 测量与计算
- 第二十一章 圆(上)
- 21.1 圆的有关概念
- 21.2 过三点的圆
- 21.3 圆的对称性
- 21.4 圆周角
- 第二十二章 圆(下)
- 22.1 直线和圆的位置关系
- 22.2 圆的切线
- 22.3 正多边形的有关计算
