第一章 三角函数单元综合检测题二(带解析)
文档属性
| 名称 | 第一章 三角函数单元综合检测题二(带解析) |  | |
| 格式 | zip | ||
| 文件大小 | 766.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-11-07 15:42:38 | ||
图片预览




文档简介
第一章 三角函数单元综合检测题二(带解析)
一、选择题(共60分)
1.下面四个命题正确的是( )
A.第一象限角必是锐角
B.小于90°的角是锐角
C.若cosα<0,则α是第二或第三象限角
D.锐角必是第一象限角
2.已知角的终边经过点,则( )
A. B. C. D.
3.若,则的值为( )
A. B. C. D.
4.下列四个函数中,既是上的增函数,又是以为周期的偶函数的是()
A. B.
C. D.
5.要得到函数y=cos()的图象,只需将函数y=sin的图象( )
A.向左平移个单位长度
B.向右平移个单位长度
C.向左平移个单位长度
D.向右平移个单位长度
6.将函数的图象向右平行移动个单位长度,再把横坐标缩短为原来的一半,纵坐标伸长为原来的3倍,则所得到的图象的函数解析式是( )【来源:21·世纪·教育·网】
A. B. C. D.
7.在直角坐标系中,一动点从点出发,沿单位圆(圆心在坐标原点半径为1的圆)圆周按逆时针方向运动弧长,到达点,则点的坐标为( )
A. B. C. D.
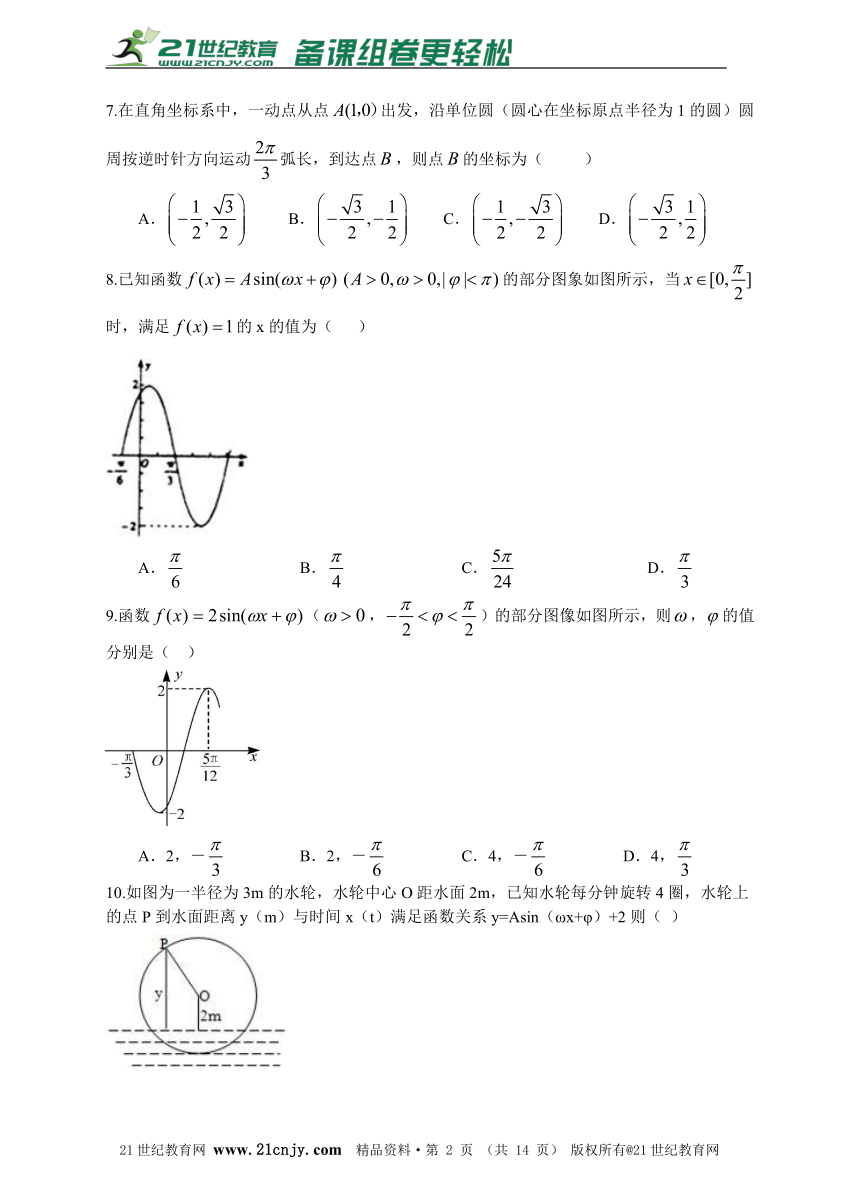
8.已知函数的部分图象如图所示,当时,满足的x的值为( )
A. B. C. D.
9.函数(,)的部分图像如图所示,则,的值分别是( )
A.2,- B.2,- C.4,- D.4,
10.如图为一半径为3m的水轮,水轮中心O距水面2m,已知水轮每分钟旋转4圈,水轮上的点P到水面距离y(m)与时间x(t)满足函数关系y=Asin(ωx+φ)+2则( )21·世纪*教育网
A.ω=,A=5 B.ω=,A=5 C.ω=,A=3 D.ω=,A=3
二、填空题(共24分)
11.若,计算:= .
12.已知角的终边过点,则__________.
13.(2015秋?凉山州期末)已知cos(α+)=,求sin(﹣α)的值 .
14.函数y=2sin(ωx+φ)(,)的部分图象如图所示,则ω和φ的值分别是__________.2·1·c·n·j·y
三、解答题(共66分)
15.(10分)已知角的终边经过点,试写出角的集合M,并把集合M中在~间的角写出来.
16.(10分)(1)求值:
(2)化简:
17.(10分)函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<)在x∈(0,7π)内取到一个最大值和一个最小值,且当x=π时,y有最大值3,当x=6π时,y有最小值-3.
(1)求此函数解析式;
(2)写出该函数的单调递增区间.
18.(12分)已知函数()的最小正周期为.
(1)求函数的单调增区间;
(2)将函数的图像向左平移个单位,再向上平移个单位,得到函数的图像.求在区间上零点的个数.21教育网
19.(12分)已知函数.
(1)求的最小正周期.
(2)若将的图象向右平移个单位,得到函数的图象,求函数在区间上的值域.
20.(12分)如图,经过村庄A有两条夹角为60°的公路AB,AC,根据规划拟在两条公路之间的区域内建一工厂P,分别在两条公路边上建两个仓库M、N (异于村庄A),要求PM=PN=MN=2(单位:千米).如何设计, 可以使得工厂产生的噪声对居民的影响最小(即工厂与村庄的距离最远).21世纪教育网版权所有
参考答案及解析
1.D
【解析】通过给变量取特殊值,举反例来可以说明某个命题不正确,可排除部分选项.
根据选项的叙述,利用象限角、终边相同的角的定义,结合三角形的知识判断A错误;锐角的定义判断B正确;象限角判断C错误;锐角的范围判断D正误.21cnjy.com
第一象限角必是锐角,显然不正确,A错误;
小于90°的角是锐角,可以是负角,所以B不正确;
若cosα<0,则α是第二或第三象限角,可以是x负半轴上的角,所以不正确.
5.A
【解析】先根据诱导公式进行化简,再由左加右减上加下减的原则可确定函数到的路线,即可得到选项.
==,
只需将函数的图象,向左平移个单位长度得到函数=的图象.
6.A
【解析】根据函数y=Asin(ωx+φ)的图象变换规则对函数的解析式进行变换即可. 由题意将函数的图象向右平行移动个单位长度, 得到函数y=cos[2(x-)]=cos(2x)的图象, 再把横坐标缩短为原来的一半,得到函数y=cos(4x)的图象, 再把纵坐标伸长为原来的3倍,得到函数y=3cos(4x)的图象, 7.A21·cn·jy·com
【解析】设点,点是的终边与单位圆的交点,由任意角三角函数的定义得
,将代入,得,解得,又因为,则,故选A.
10.D
【解析】根据题意,水轮旋转一周所用的时间为一个周期,由周期公式,T=求解;A为最大振幅,由图象知到最高点时即为A值. 已知水轮每分钟旋转4圈 ∴ω= 又∵半径为3m,水轮中心O距水面2m, ∴最高点为5,即A=3, 11..www.21-cn-jy.com
【解析】因为,所以应填.
12.
【解析】依题意,,又由,且终边在第四象限,所以,故正确答案为.
13.
【解析】原式中的角度变形后,利用诱导公式化简,将已知等式代入计算即可求出值.
∵cos(α+)=,
∴sin(﹣α)=sin[﹣(α+)]=cos(α+)=,
14.ω=2;φ=.
【解析】由图象得T=-(-)=π,
16.(1)11;(2)-1
【解析】(1)考察到了指数的运算,和对数的基本运算,所用公式,,;
(2)熟记诱导公式,将问题转化为关于的同名三角函数值的计算.
(1)原式
(2)原式
(2)令,得10kπ-4π≤x≤10kπ+π,k∈Z.
∴函数的单调递增区间为,.
18.(1)函数的单调增区间;
(2)在上有个零点.
【解析】(1)先由三角函数的周期计算公式得到,从而可确定,将当成一个整体,由正弦函数的性质得到,解出的范围,写成区间即是所求函数的单调递增区间;(2)将函数的图像向左平移个单位,再向上平移1个单位,得到的图像,即,由正弦函数的图像与性质得到该函数在一个周期内函数零点的个数,
所以函数在每个周期上恰有两个零点,恰为个周期,故在上有个零点.
19.(1);(2).
【解析】(1)利用二倍角公式,诱导公式,化一公式进行化简为,利用;
(2)利用左加右减得到的图像,求的范围,再根据的图像,计算的值域.
由题设可得
(1)函数最小正周期为2
(2)易知
由
值域为
20.为时,工厂产生的噪声对居民的影响最小。
因为,所以.
当且仅当,即时,取得最大值12,即取得最大值.
答:设为时,工厂产生的噪声对居民的影响最小.
一、选择题(共60分)
1.下面四个命题正确的是( )
A.第一象限角必是锐角
B.小于90°的角是锐角
C.若cosα<0,则α是第二或第三象限角
D.锐角必是第一象限角
2.已知角的终边经过点,则( )
A. B. C. D.
3.若,则的值为( )
A. B. C. D.
4.下列四个函数中,既是上的增函数,又是以为周期的偶函数的是()
A. B.
C. D.
5.要得到函数y=cos()的图象,只需将函数y=sin的图象( )
A.向左平移个单位长度
B.向右平移个单位长度
C.向左平移个单位长度
D.向右平移个单位长度
6.将函数的图象向右平行移动个单位长度,再把横坐标缩短为原来的一半,纵坐标伸长为原来的3倍,则所得到的图象的函数解析式是( )【来源:21·世纪·教育·网】
A. B. C. D.
7.在直角坐标系中,一动点从点出发,沿单位圆(圆心在坐标原点半径为1的圆)圆周按逆时针方向运动弧长,到达点,则点的坐标为( )
A. B. C. D.
8.已知函数的部分图象如图所示,当时,满足的x的值为( )
A. B. C. D.
9.函数(,)的部分图像如图所示,则,的值分别是( )
A.2,- B.2,- C.4,- D.4,
10.如图为一半径为3m的水轮,水轮中心O距水面2m,已知水轮每分钟旋转4圈,水轮上的点P到水面距离y(m)与时间x(t)满足函数关系y=Asin(ωx+φ)+2则( )21·世纪*教育网
A.ω=,A=5 B.ω=,A=5 C.ω=,A=3 D.ω=,A=3
二、填空题(共24分)
11.若,计算:= .
12.已知角的终边过点,则__________.
13.(2015秋?凉山州期末)已知cos(α+)=,求sin(﹣α)的值 .
14.函数y=2sin(ωx+φ)(,)的部分图象如图所示,则ω和φ的值分别是__________.2·1·c·n·j·y
三、解答题(共66分)
15.(10分)已知角的终边经过点,试写出角的集合M,并把集合M中在~间的角写出来.
16.(10分)(1)求值:
(2)化简:
17.(10分)函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<)在x∈(0,7π)内取到一个最大值和一个最小值,且当x=π时,y有最大值3,当x=6π时,y有最小值-3.
(1)求此函数解析式;
(2)写出该函数的单调递增区间.
18.(12分)已知函数()的最小正周期为.
(1)求函数的单调增区间;
(2)将函数的图像向左平移个单位,再向上平移个单位,得到函数的图像.求在区间上零点的个数.21教育网
19.(12分)已知函数.
(1)求的最小正周期.
(2)若将的图象向右平移个单位,得到函数的图象,求函数在区间上的值域.
20.(12分)如图,经过村庄A有两条夹角为60°的公路AB,AC,根据规划拟在两条公路之间的区域内建一工厂P,分别在两条公路边上建两个仓库M、N (异于村庄A),要求PM=PN=MN=2(单位:千米).如何设计, 可以使得工厂产生的噪声对居民的影响最小(即工厂与村庄的距离最远).21世纪教育网版权所有
参考答案及解析
1.D
【解析】通过给变量取特殊值,举反例来可以说明某个命题不正确,可排除部分选项.
根据选项的叙述,利用象限角、终边相同的角的定义,结合三角形的知识判断A错误;锐角的定义判断B正确;象限角判断C错误;锐角的范围判断D正误.21cnjy.com
第一象限角必是锐角,显然不正确,A错误;
小于90°的角是锐角,可以是负角,所以B不正确;
若cosα<0,则α是第二或第三象限角,可以是x负半轴上的角,所以不正确.
5.A
【解析】先根据诱导公式进行化简,再由左加右减上加下减的原则可确定函数到的路线,即可得到选项.
==,
只需将函数的图象,向左平移个单位长度得到函数=的图象.
6.A
【解析】根据函数y=Asin(ωx+φ)的图象变换规则对函数的解析式进行变换即可. 由题意将函数的图象向右平行移动个单位长度, 得到函数y=cos[2(x-)]=cos(2x)的图象, 再把横坐标缩短为原来的一半,得到函数y=cos(4x)的图象, 再把纵坐标伸长为原来的3倍,得到函数y=3cos(4x)的图象, 7.A21·cn·jy·com
【解析】设点,点是的终边与单位圆的交点,由任意角三角函数的定义得
,将代入,得,解得,又因为,则,故选A.
10.D
【解析】根据题意,水轮旋转一周所用的时间为一个周期,由周期公式,T=求解;A为最大振幅,由图象知到最高点时即为A值. 已知水轮每分钟旋转4圈 ∴ω= 又∵半径为3m,水轮中心O距水面2m, ∴最高点为5,即A=3, 11..www.21-cn-jy.com
【解析】因为,所以应填.
12.
【解析】依题意,,又由,且终边在第四象限,所以,故正确答案为.
13.
【解析】原式中的角度变形后,利用诱导公式化简,将已知等式代入计算即可求出值.
∵cos(α+)=,
∴sin(﹣α)=sin[﹣(α+)]=cos(α+)=,
14.ω=2;φ=.
【解析】由图象得T=-(-)=π,
16.(1)11;(2)-1
【解析】(1)考察到了指数的运算,和对数的基本运算,所用公式,,;
(2)熟记诱导公式,将问题转化为关于的同名三角函数值的计算.
(1)原式
(2)原式
(2)令,得10kπ-4π≤x≤10kπ+π,k∈Z.
∴函数的单调递增区间为,.
18.(1)函数的单调增区间;
(2)在上有个零点.
【解析】(1)先由三角函数的周期计算公式得到,从而可确定,将当成一个整体,由正弦函数的性质得到,解出的范围,写成区间即是所求函数的单调递增区间;(2)将函数的图像向左平移个单位,再向上平移1个单位,得到的图像,即,由正弦函数的图像与性质得到该函数在一个周期内函数零点的个数,
所以函数在每个周期上恰有两个零点,恰为个周期,故在上有个零点.
19.(1);(2).
【解析】(1)利用二倍角公式,诱导公式,化一公式进行化简为,利用;
(2)利用左加右减得到的图像,求的范围,再根据的图像,计算的值域.
由题设可得
(1)函数最小正周期为2
(2)易知
由
值域为
20.为时,工厂产生的噪声对居民的影响最小。
因为,所以.
当且仅当,即时,取得最大值12,即取得最大值.
答:设为时,工厂产生的噪声对居民的影响最小.
