2.1.2 空间中直线与直线之间的位置关系第1课时
文档属性
| 名称 | 2.1.2 空间中直线与直线之间的位置关系第1课时 |  | |
| 格式 | rar | ||
| 文件大小 | 86.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-05-20 20:49:00 | ||
图片预览


文档简介
课件19张PPT。2.1.2 空间中直线与直线之间的位置关系
第1课时
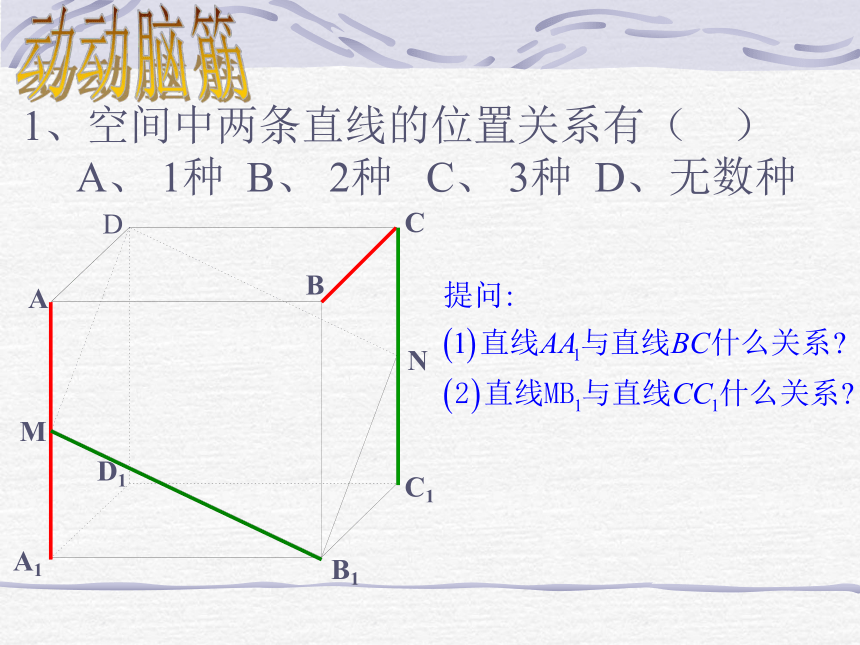
授课人:李平请叙述三条公理和三条推论回顾如果一条直线上的两点在一个平面内,那么这条直线在此平面内过不在一条直线上的三点,有且只有一个平面 经过一条直线和这条直线外的一点有且只有一个平面 经过两条相交直线,有且只有一个平面经过两条平行直线,有且只有一个平面如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线 1、空间中两条直线的位置关系有( )
A、 1种 B、 2种 C、 3种 D、无数种 动动脑筋讲授新课异面直线的定义:
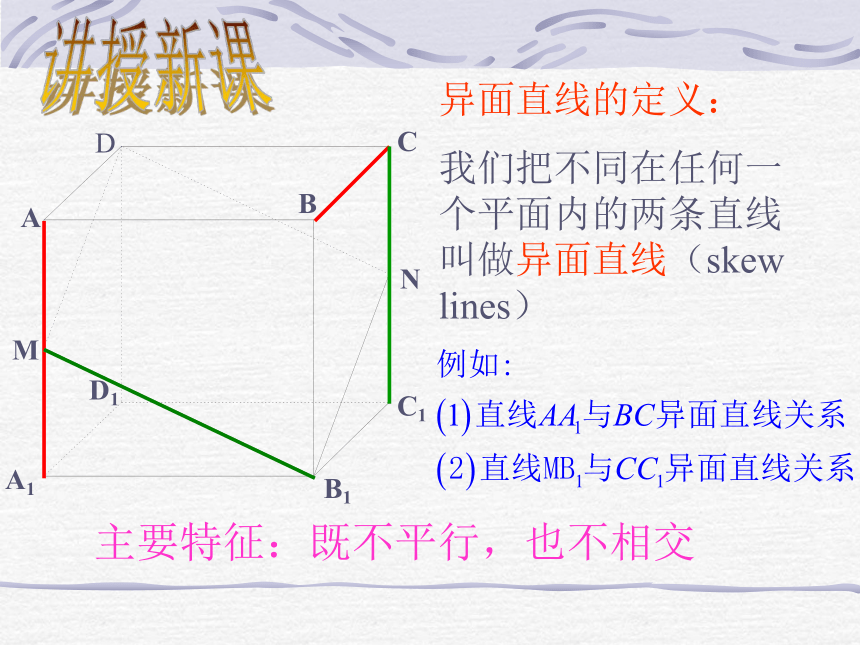
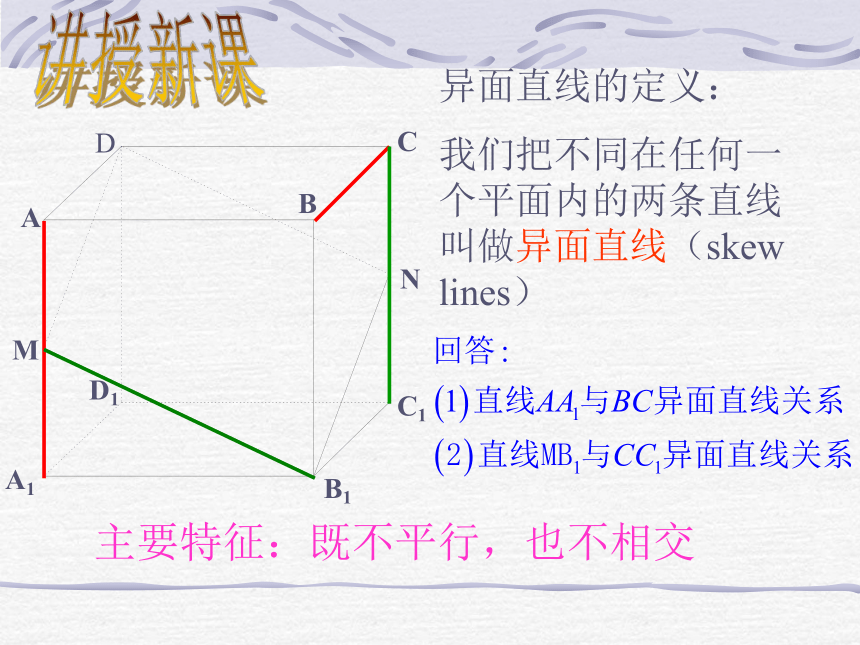
我们把不同在任何一个平面内的两条直线叫做异面直线(skew lines)主要特征:既不平行,也不相交讲授新课异面直线的定义:
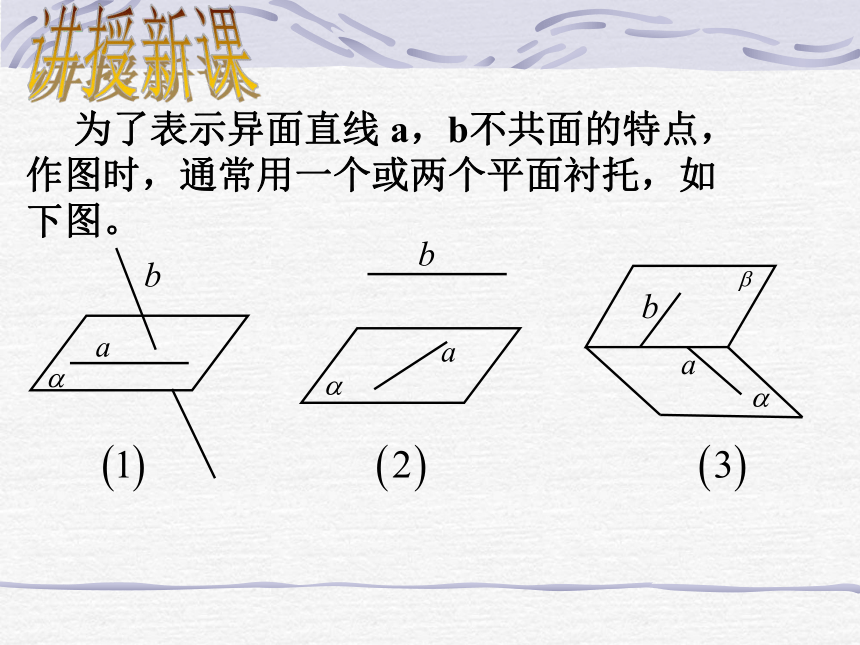
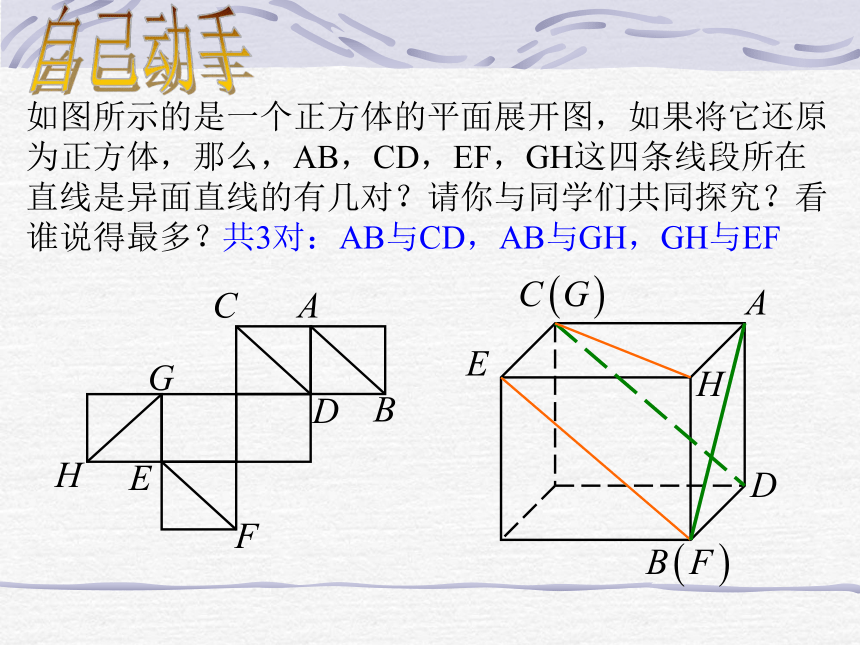
我们把不同在任何一个平面内的两条直线叫做异面直线(skew lines)主要特征:既不平行,也不相交 为了表示异面直线 a,b不共面的特点,作图时,通常用一个或两个平面衬托,如下图。讲授新课如图所示的是一个正方体的平面展开图,如果将它还原为正方体,那么,AB,CD,EF,GH这四条线段所在直线是异面直线的有几对?请你与同学们共同探究?看谁说得最多?共3对:AB与CD,AB与GH,GH与EF自己动手空间两条不重合直线的位图关系有且只有三种:讲授新课1、空间中两条直线的位置关系有( )
A、 1种 B、 2种 C、 3种 D、无数种 2、空间中两条平行或相交的直线一定( )
A、 共面
B、异面
C、可能共面也可能异面
D、既不共面也不异面课堂练习 3、“a,b是异面直线”是指
① a∩b=Φ且a不平行于b;
② a ? 平面?,b ? 平面?且a∩b=Φ
③ a ? 平面?,b ? 平面?
④ 不存在平面?,能使a ? ?且b ? ?成立
上述结论中,正确的是( )
(A)①② (B)①③ (C)①④ (D)③④注意:不能误认为分别在不同平面内的两直线 就是异面直线.如:课堂练习1、两条直线a,b分别和异面直线c,d都相交,则直线a, b的位置关系是( )
(A)一定是异面直线
(B)一定是相交直线
(C)可能是平行直线
(D)可能是异面直线,也可能是相交直线
2、一条直线和两条异面直线中的一条平行,则它和另一 条的位置关系是( )
(A)平行 (B)相交 (C)异面 (D)相交或异面组内讨论组内讨论3、分别在两个平面内的两条直线间的位置关系是( )
(A)异面 (B)平行
(C)相交 (D)以上都有可能
4、异面直线a,b满足a??,b??,?∩?=l,则l与a,b的位置关系一定是( )
(A)l与a,b都相交
(B)l至少与a,b中的一条相交
(C)l至多与a,b中的一条相交
(D)l至少与a,b中的一条平行异面直线的判定定理:
过平外一点与平面内一点的直线,和平面内不经过该点的直线是异面直线。分析:
证明两条直线异面,如果从定义出发直接证明,即需要抓住“不同在任何一个平面内”中的“任何”,若一个平面一个平面地寻找是不可能实现的。因此,必须找到一个间接法来证明,反证法是一种比较有效的好方法。补充定理证明定理异面直线的判定方法:
定义法:此时需借助反证法,假设两条直线不异面,根据空间两条直线的位置关系,这两条直线一定共面,即这两条直线可能相交,也可能平行,然后推出 矛盾即可。
定理法:即用判定定理,用该方法证明时,必须阐述定理满足的条件: 然后可以推出
归纳总结谢谢观赏
第1课时
授课人:李平请叙述三条公理和三条推论回顾如果一条直线上的两点在一个平面内,那么这条直线在此平面内过不在一条直线上的三点,有且只有一个平面 经过一条直线和这条直线外的一点有且只有一个平面 经过两条相交直线,有且只有一个平面经过两条平行直线,有且只有一个平面如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线 1、空间中两条直线的位置关系有( )
A、 1种 B、 2种 C、 3种 D、无数种 动动脑筋讲授新课异面直线的定义:
我们把不同在任何一个平面内的两条直线叫做异面直线(skew lines)主要特征:既不平行,也不相交讲授新课异面直线的定义:
我们把不同在任何一个平面内的两条直线叫做异面直线(skew lines)主要特征:既不平行,也不相交 为了表示异面直线 a,b不共面的特点,作图时,通常用一个或两个平面衬托,如下图。讲授新课如图所示的是一个正方体的平面展开图,如果将它还原为正方体,那么,AB,CD,EF,GH这四条线段所在直线是异面直线的有几对?请你与同学们共同探究?看谁说得最多?共3对:AB与CD,AB与GH,GH与EF自己动手空间两条不重合直线的位图关系有且只有三种:讲授新课1、空间中两条直线的位置关系有( )
A、 1种 B、 2种 C、 3种 D、无数种 2、空间中两条平行或相交的直线一定( )
A、 共面
B、异面
C、可能共面也可能异面
D、既不共面也不异面课堂练习 3、“a,b是异面直线”是指
① a∩b=Φ且a不平行于b;
② a ? 平面?,b ? 平面?且a∩b=Φ
③ a ? 平面?,b ? 平面?
④ 不存在平面?,能使a ? ?且b ? ?成立
上述结论中,正确的是( )
(A)①② (B)①③ (C)①④ (D)③④注意:不能误认为分别在不同平面内的两直线 就是异面直线.如:课堂练习1、两条直线a,b分别和异面直线c,d都相交,则直线a, b的位置关系是( )
(A)一定是异面直线
(B)一定是相交直线
(C)可能是平行直线
(D)可能是异面直线,也可能是相交直线
2、一条直线和两条异面直线中的一条平行,则它和另一 条的位置关系是( )
(A)平行 (B)相交 (C)异面 (D)相交或异面组内讨论组内讨论3、分别在两个平面内的两条直线间的位置关系是( )
(A)异面 (B)平行
(C)相交 (D)以上都有可能
4、异面直线a,b满足a??,b??,?∩?=l,则l与a,b的位置关系一定是( )
(A)l与a,b都相交
(B)l至少与a,b中的一条相交
(C)l至多与a,b中的一条相交
(D)l至少与a,b中的一条平行异面直线的判定定理:
过平外一点与平面内一点的直线,和平面内不经过该点的直线是异面直线。分析:
证明两条直线异面,如果从定义出发直接证明,即需要抓住“不同在任何一个平面内”中的“任何”,若一个平面一个平面地寻找是不可能实现的。因此,必须找到一个间接法来证明,反证法是一种比较有效的好方法。补充定理证明定理异面直线的判定方法:
定义法:此时需借助反证法,假设两条直线不异面,根据空间两条直线的位置关系,这两条直线一定共面,即这两条直线可能相交,也可能平行,然后推出 矛盾即可。
定理法:即用判定定理,用该方法证明时,必须阐述定理满足的条件: 然后可以推出
归纳总结谢谢观赏
