26.2.3求二次函数关系式课文练习(解析版)
文档属性
| 名称 | 26.2.3求二次函数关系式课文练习(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 145.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-11-05 22:31:27 | ||
图片预览



文档简介
26.2.3求二次函数关系式
一.选择题(共8小题)
1.如果二次函数y=ax2+bx+c(a≠0)的图象如图所示,那么( )
( http: / / www.21cnjy.com )
A.a<0,b>0,c>0
B.a>0,b<0,c>0
C.a>0,b<0,c<0
D.a>0,b>0,c<0
2.如果二次函数y=ax2+bx+c的图象如图所示,那么下列判断正确的是( )
( http: / / www.21cnjy.com )
A.a>0,c>0
B.a<0,c>0
C.a>0,c<0
D.a<0,c<0
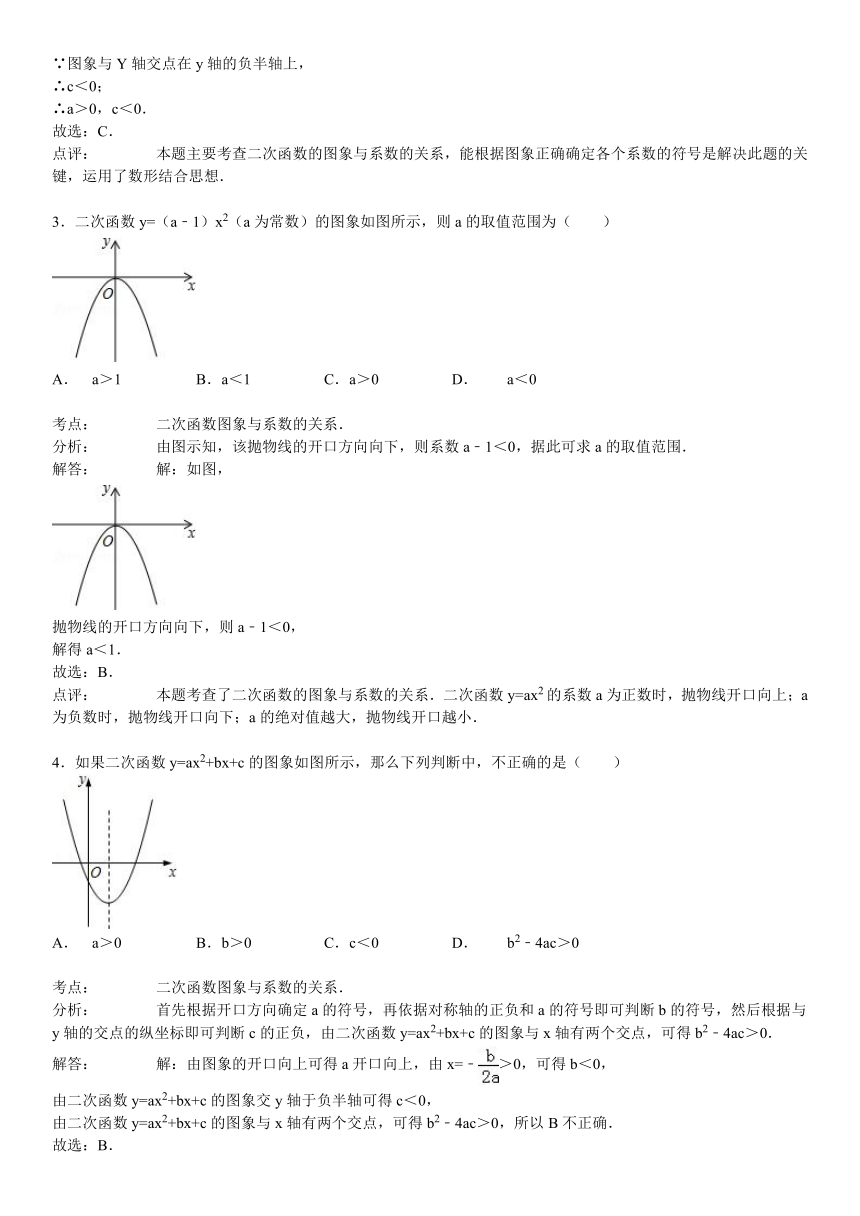
3.二次函数y=(a﹣1)x2(a为常数)的图象如图所示,则a的取值范围为( )
( http: / / www.21cnjy.com )
A.a>1
B.a<1
C.a>0
D.a<0
4.如果二次函数y=ax2+bx+c的图象如图所示,那么下列判断中,不正确的是( )
( http: / / www.21cnjy.com )
A.a>0
B.b>0
C.c<0
D.b2﹣4ac>0
5.抛物线y=(m﹣1)x2﹣mx﹣m2+1的图象过原点,则m的值为( )
A.±1
B.0
C.1
D.﹣1
6.(已知点(﹣2,4)在抛物线y=ax2上,则a的值是( )
A.﹣1
B.1
C.±1
D.
7.将二次函数y=x2的图象向下平移1个单位,再向右平移1个单位后所得图象的函数表达式为( )
A.y=(x+1)2+1
B.y=(x+1)2﹣1
C.y=(x﹣1)2+1
D.y=(x﹣1)2﹣1
8.将抛物线y=(x﹣1)2向左平移2个单位,所得抛物线的表达式为( )
A.y=(x+1)2
B.y=(x﹣3)2
C.y=(x﹣1)2+2
D.y=(x﹣1)2﹣2
二.填空题(共6小题)
9.已知抛物线经过点(5,﹣3),其对称轴为直线x=4,则抛物线一定经过另一点的坐标是 _________ .
10.如果二次函数y=(m﹣1)x2+5x+m2﹣1的图象经过原点,那么m= _________ .
11.若点(﹣2,a),(﹣3,b)都在
( http: / / www.21cnjy.com )二次函数y=x2+2x+m的图象上,比较a、b的大小:a _________ b.(填“>”“<”或“=”).
12.已知二次函数y=x2+2x﹣7的一个函数值是8,那么对应的自变量x的值是 _________ .
13.抛物线y=x2+2向左平移2个单位得到的抛物线表达式为 _________ .
14.如果将抛物线y=3x2平移,使平移后的抛物线顶点坐标为(2,2),那么平移后的抛物线的表达式为 _________ .
三.解答题(共8小题)
15.抛物线y=ax2+bx+c(a≠0)向右平移2个单位得到抛物线y=a(x﹣3)2﹣1,且平移后的抛物线经过点A(2,1).
(1)求平移后抛物线的解析式;
(2)设原抛物线与y轴的交点为B,顶点为P,平移后抛物线的对称轴与x轴交于点M,求△BPM的面积.
( http: / / www.21cnjy.com )
16.在直角坐标平面内,抛物线y=ax2+bx+c经过原点O、A(﹣2,﹣2)与B(1,﹣5)三点.
(1)求抛物线的表达式;
(2)写出该抛物线的顶点坐标.
17.如图,已知二次函数的图象过A、C、B三点,点A的坐标为(﹣1,0),点B的坐标为(4,0),点C在y轴正半轴上,且AB=OC.
(1)求点C的坐标;
(2)求二次函数的解析式,并化成一般形式.
( http: / / www.21cnjy.com )
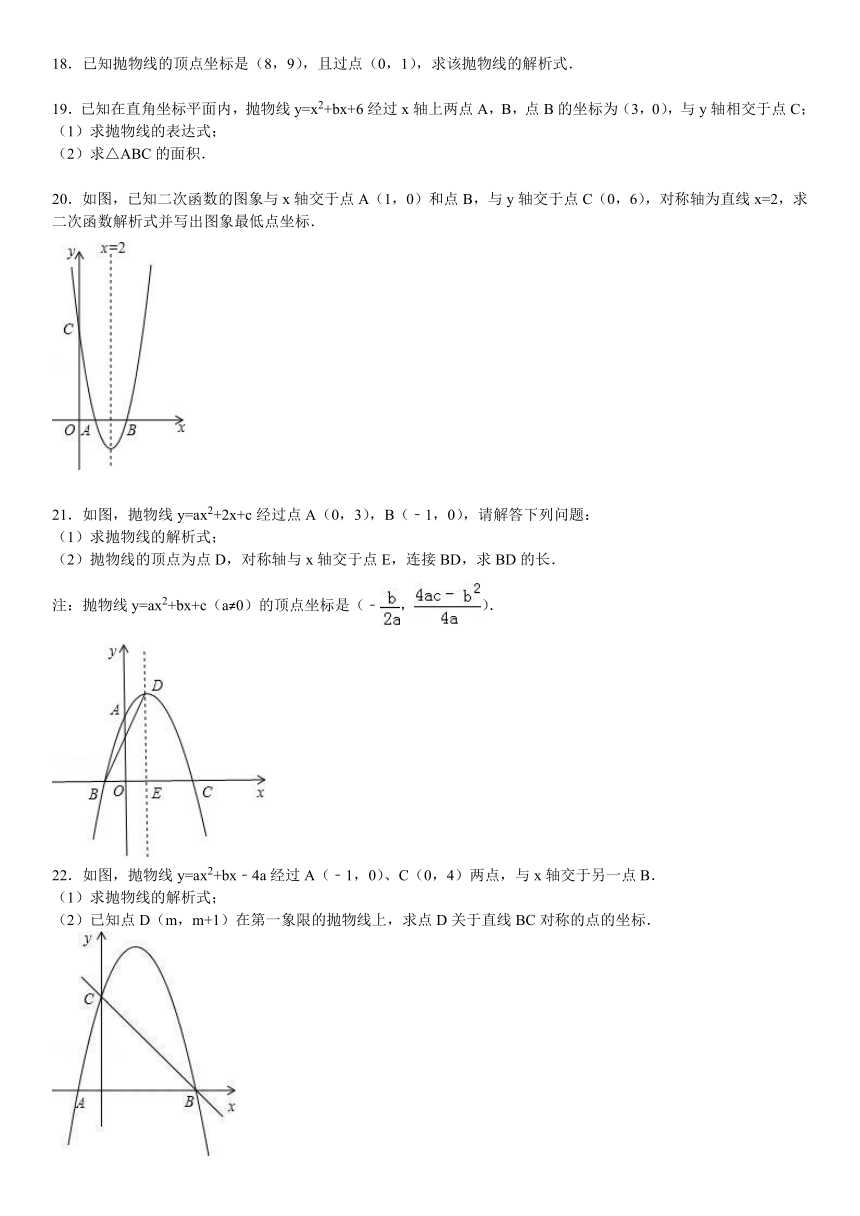
18.已知抛物线的顶点坐标是(8,9),且过点(0,1),求该抛物线的解析式.
19.已知在直角坐标平面内,抛物线y=x2+bx+6经过x轴上两点A,B,点B的坐标为(3,0),与y轴相交于点C;
(1)求抛物线的表达式;
(2)求△ABC的面积.
20.如图,已知二次函数的图象与x轴交于点
( http: / / www.21cnjy.com )A(1,0)和点B,与y轴交于点C(0,6),对称轴为直线x=2,求二次函数解析式并写出图象最低点坐标.
( http: / / www.21cnjy.com )
21.如图,抛物线y=ax2+2x+c经过点A(0,3),B(﹣1,0),请解答下列问题:
(1)求抛物线的解析式;
(2)抛物线的顶点为点D,对称轴与x轴交于点E,连接BD,求BD的长.
注:抛物线y=ax2+bx+c(a≠0)的顶点坐标是(﹣,).
( http: / / www.21cnjy.com )
22.如图,抛物线y=ax2+bx﹣4a经过A(﹣1,0)、C(0,4)两点,与x轴交于另一点B.
(1)求抛物线的解析式;
(2)已知点D(m,m+1)在第一象限的抛物线上,求点D关于直线BC对称的点的坐标.
( http: / / www.21cnjy.com )
26.2.3求二次函数关系式
参考答案与试题解析
一.选择题(共8小题)
1.如果二次函数y=ax2+bx+c(a≠0)的图象如图所示,那么( )
( http: / / www.21cnjy.com )
A.
a<0,b>0,c>0
B.a>0,b<0,c>0
C.a>0,b<0,c<0
D.
a>0,b>0,c<0
考点:
二次函数图象与系数的关系.
分析:
首先根据开口方向确定a的符号,再依据对称轴的正负和a的符号即可判断b的符号,然后根据与y轴的交点的纵坐标即可判断c的正负,由此得出答案即可.
解答:
解:∵图象开口方向向上,
∴a>0;
∵图象的对称轴在x轴的正半轴上,
∴﹣>0,
∵a>0,
∴b<0;
∵图象与Y轴交点在y轴的负半轴上,
∴c<0;
∴a>0,b<0,c<0.
故选:C.
点评:
本题主要考查二次函数的图象与系数的关系,能根据图象正确确定各个系数的符号是解决此题的关键,运用了数形结合思想.
2.如果二次函数y=ax2+bx+c的图象如图所示,那么下列判断正确的是( )
( http: / / www.21cnjy.com )
A.
a>0,c>0
B.a<0,c>0
C.a>0,c<0
D.
a<0,c<0
考点:
二次函数图象与系数的关系.
分析:
首先根据开口方向确定a的符号,再依据与y轴的交点的纵坐标即可判断c的正负,由此解决问题.
解答:
解:∵图象开口方向向上,
∴a>0;
∵图象与Y轴交点在y轴的负半轴上,
∴c<0;
∴a>0,c<0.
故选:C.
点评:
本题主要考查二次函数的图象与系数的关系,能根据图象正确确定各个系数的符号是解决此题的关键,运用了数形结合思想.
3.二次函数y=(a﹣1)x2(a为常数)的图象如图所示,则a的取值范围为( )
( http: / / www.21cnjy.com )
A.
a>1
B.a<1
C.a>0
D.
a<0
考点:
二次函数图象与系数的关系.
分析:
由图示知,该抛物线的开口方向向下,则系数a﹣1<0,据此可求a的取值范围.
解答:
解:如图,
( http: / / www.21cnjy.com )
抛物线的开口方向向下,则a﹣1<0,
解得a<1.
故选:B.
点评:
本题考查了二次函数的图象与系数的关
( http: / / www.21cnjy.com )系.二次函数y=ax2的系数a为正数时,抛物线开口向上;a为负数时,抛物线开口向下;a的绝对值越大,抛物线开口越小.
4.如果二次函数y=ax2+bx+c的图象如图所示,那么下列判断中,不正确的是( )
( http: / / www.21cnjy.com )
A.
a>0
B.b>0
C.c<0
D.
b2﹣4ac>0
考点:
二次函数图象与系数的关系.
分析:
首先根据开口方向确
( http: / / www.21cnjy.com )定a的符号,再依据对称轴的正负和a的符号即可判断b的符号,然后根据与y轴的交点的纵坐标即可判断c的正负,由二次函数y=ax2+bx+c的图象与x轴有两个交点,可得b2﹣4ac>0.
解答:
解:由图象的开口向上可得a开口向上,由x=﹣>0,可得b<0,
由二次函数y=ax2+bx+c的图象交y轴于负半轴可得c<0,
由二次函数y=ax2+bx+c的图象与x轴有两个交点,可得b2﹣4ac>0,所以B不正确.
故选:B.
点评:
本题主要考查二次函数的图象与系数的关系,能根据图象正确确定各个系数的符号是解决此题的关键,此题运用了数形结合思想.
5.抛物线y=(m﹣1)x2﹣mx﹣m2+1的图象过原点,则m的值为( )
A.
±1
B.0
C.1
D.
﹣1
考点:
二次函数图象上点的坐标特征;二次函数的定义.
专题:
计算题.
分析:
根据二次函数图象上点的坐标特征得到﹣m2+1=0,解得m1=1,m2=﹣1,然后根据二次函数的定义确定m的值.
解答:
解:把(0,0)代入y=(m﹣1)x2﹣mx﹣m2+1得﹣m2+1=0,解得m1=1,m2=﹣1,
而m﹣1≠0,
所以m=﹣1.
故选D.
点评:
本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.也考查了二次函数的定义.
6.已知点(﹣2,4)在抛物线y=ax2上,则a的值是( )
A.
﹣1
B.1
C.±1
D.
考点:
二次函数图象上点的坐标特征.
专题:
计算题.
分析:
根据二次函数图象上点的坐标特征,把点(﹣2,4)代入y=ax2中得到a的方程,然后解方程即可.
解答:
解:∵点(﹣2,4)在抛物线y=ax2上,
∴a (﹣2)2=4,
∴a=1.
故选B.
点评:
本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.
7.将二次函数y=x2的图象向下平移1个单位,再向右平移1个单位后所得图象的函数表达式为( )
A.
y=(x+1)2+1
B.y=(x+1)2﹣1
C.y=(x﹣1)2+1
D.
y=(x﹣1)2﹣1
考点:
二次函数图象与几何变换.
分析:
先得到抛物线y=x2的顶点坐标
( http: / / www.21cnjy.com )为(0,0),再利用点的平移规律得到点(0,0)平移后对应点的坐标为(1,﹣1),然后根据顶点式写出平移的抛物线解析式.
解答:
解:抛物线y=x2的顶点坐标为(0,0),把点(0,0)向右平移1个单位,向下平移1个单位得到对应点的坐标为(1,﹣1),所以平移后的新图象的函数表达式为y=(x﹣1)2﹣1.
故选:D.
点评:
本题考查了二次函数图象上点的坐标特征:由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.
8.将抛物线y=(x﹣1)2向左平移2个单位,所得抛物线的表达式为( )
A.
y=(x+1)2
B.y=(x﹣3)2
C.y=(x﹣1)2+2
D.
y=(x﹣1)2﹣2
考点:
二次函数图象与几何变换.
专题:
几何变换.
分析:
先根据二次函数的性质得到抛
( http: / / www.21cnjy.com )物线y=(x﹣1)2的顶点坐标为(1,0),再利用点平移的规律得到点(1,0)平移后对应点的坐标为(﹣1,0),然后根据顶点式写出平移后抛物线的表达式.
解答:
解:抛物线y=(x﹣1)2的顶点坐标为(1,0),点(1,0)向左平移2个单位得到对应点的坐标为(﹣1,0),所以平移后抛物线的表达式为y=(x+1)2.
故选A.
点评:
本题考查了二次函数图象与几何变换:由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.
二.填空题(共6小题)
9.已知抛物线经过点(5,﹣3),其对称轴为直线x=4,则抛物线一定经过另一点的坐标是 (3,﹣3) .
考点:
二次函数图象上点的坐标特征.
分析:
根据二次函数的对称性求解即可.
解答:
解:∵点(5,﹣3)关于对称轴直线x=4的对称点为(3,﹣3),
∴抛物线一定经过另一点的坐标是(3,﹣3).
故答案为:(3,﹣3).
点评:
本题考查了二次函数图象上点的坐标特征,主要利用了二次函数的对称性.
10.如果二次函数y=(m﹣1)x2+5x+m2﹣1的图象经过原点,那么m= ﹣1 .
考点:
二次函数图象上点的坐标特征;二次函数的定义.
分析:
把原点坐标代入函数解析式求解即可得到m的值,再根据二次项系数不等于0求出m≠1.
解答:
解:∵二次函数y=(m﹣1)x2+5x+m2﹣1的图象经过原点,
∴m2﹣1=0,
解得m=±1,
∵函数为二次函数,
∴m﹣1≠0,
解得m≠1,
所以,m=﹣1.
故答案为:﹣1.
点评:
本题考查了二次函数图象上点的坐标特征,二次函数的定义,要注意二次项系数不等于0.
11.若点(﹣2,a),(﹣3,b)都在二次函数y=x2+2x+m的图象上,比较a、b的大小:a < b.(填“>”“<”或“=”).
考点:
二次函数图象上点的坐标特征.
分析:
根据二次函数图象上点的坐标特征计算出自变量为﹣2和﹣3时的函数值,然后比较函数值的大小即可.
解答:
解:∵点(﹣2,a),(﹣3,b)都在二次函数y=x2+2x+m的图象,
∴a=x2+2x+m=4﹣4+m=4,b=x2+2x+m=9﹣6+m=3+m,
∴a<b.
故答案为<.
点评:
本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.
12.已知二次函数y=x2+2x﹣7的一个函数值是8,那么对应的自变量x的值是 ﹣5或3 .
考点:
二次函数图象上点的坐标特征.
分析:
把函数值代入函数解析式,解关于x的一元二次方程即可.
解答:
解:y=8时,x2+2x﹣7=8,
整理得,x2+2x﹣15=0,
解得x1=﹣5,x2=3,
所以,对应的自变量x的值是﹣5或3.
故答案为:﹣5或3.
点评:
本题考查了二次函数图象上点的坐标特征,一元二次方程的解法,把函数值代入函数解析式得到方程是解题的关键.
13.抛物线y=x2+2向左平移2个单位得到的抛物线表达式为 y=(x+2)2+2 .
考点:
二次函数图象与几何变换.
分析:
已知抛物线解析式为顶点式,顶点坐标为(0,2),则平移后顶点坐标为(﹣2,2),由抛物线的顶点式可求平移后的抛物线解析式.
解答:
解:∵y=x2+2顶点坐标为(0,2),
∴向左平移2个单位后顶点坐标为(﹣2,2),
∴所得新抛物线的表达式为y=(x+2)2+2.
故答案为:y=(x+2)2+2.
点评:
本题考查了二次函数图象与几何变换.关键是把抛物线的平移理解为顶点的平移,根据顶点式求抛物线解析式.
14.如果将抛物线y=3x2平移,使平移后的抛物线顶点坐标为(2,2),那么平移后的抛物线的表达式为 y=3(x﹣2)2+2 .
考点:
二次函数图象与几何变换.
分析:
平移不改变抛物线的开口方向与开口大小,即解析式的二次项系数不变,根据抛物线的顶点式可求抛物线解析式.
解答:
解:∵原抛物线解析式为y=3x2,的顶点坐标是(0,0),平移后抛物线顶点坐标为(2,2),
∴平移后的抛物线的表达式为:y=3(x﹣2)2+2.
故答案为:y=3(x﹣2)2+2.
点评:
本题考查了抛物线的平移与解析式变化的关系.关键是明确抛物线的平移实质上是顶点的平移,能用顶点式表示平移后的抛物线解析式.
三.解答题(共8小题)
15.抛物线y=ax2+bx+c(a≠0)向右平移2个单位得到抛物线y=a(x﹣3)2﹣1,且平移后的抛物线经过点A(2,1).
(1)求平移后抛物线的解析式;
(2)设原抛物线与y轴的交点为B,顶点为P,平移后抛物线的对称轴与x轴交于点M,求△BPM的面积.
( http: / / www.21cnjy.com )
考点:
二次函数图象与几何变换.
分析:
(1)把点A代入平移后的抛物线y=a(x﹣3)2﹣1来求a的值;
(2)根据平移前、后的函数解析式,然后求出B、P、M三点的坐标,根据三角形的面积公式即可求出△BPM的面积.
解答:
解:(1)把点A(2,1)代入y=a(x﹣3)2﹣1,得
1=a(2﹣3)2﹣1,
整理,得
1=a﹣1,
解得
a=2.
则平移后的抛物线解析式为:y=2(x﹣3)2﹣1;
(2)由(1)知,平移后的抛物线解析式为:y=2(x﹣3)2﹣1,则M(3,0)
∵抛物线y=ax2+bx+c(a≠0)向右平移2个单位得到抛物线y=2(x﹣3)2﹣1,
∴平移前的抛物线解析式为:y=2(x﹣1)2﹣1.
∴P(1,﹣1).
令x=0,则y=1.
故B(0,1),
∴BM=
∴S△BPM=BM yP=××1=.
( http: / / www.21cnjy.com )
点评:
本题主要考查了二次函数解析式的确定、图形的面积求法、函数图象交点等知识及综合应用知识、解决问题的能力.
16.在直角坐标平面内,抛物线y=ax2+bx+c经过原点O、A(﹣2,﹣2)与B(1,﹣5)三点.
(1)求抛物线的表达式;
(2)写出该抛物线的顶点坐标.
考点:
待定系数法求二次函数解析式;二次函数的性质.
分析:
(1)把原点O、A(﹣2,﹣2)与B(1,﹣5)三点分别代入函数解析式,求得a、b、c的数值得出函数解析式即可;
(2)把函数解析式化为顶点式,得出顶点坐标即可.
解答:
解:(1)∵抛物线y=ax2+bx+c经过原点O、A(﹣2,﹣2)与B(1,﹣5)三点,
∴,
解得:,
∴抛物线的表达式为y=﹣2x2﹣3x.
(2)y=﹣2x2﹣3x
=y=﹣2(x+)2+,
抛物线的顶点坐标为(﹣,).
点评:
此题考查待定系数法求函数解析式,以及利用配方法求得顶点坐标.
17.如图,已知二次函数的图象过A、C、B三点,点A的坐标为(﹣1,0),点B的坐标为(4,0),点C在y轴正半轴上,且AB=OC.
(1)求点C的坐标;
(2)求二次函数的解析式,并化成一般形式.
( http: / / www.21cnjy.com )
考点:
待定系数法求二次函数解析式.
分析:
(1)根据题目所给的信息可以知道OC=AB=5,点C在y轴上可以写出点C的坐标;
(2)二次函数图象经过点A、B、C;这三个点的坐标已知,根据三点法确定这一二次函数解析式.
解答:
解:(1)∵点A的坐标为(﹣1,0),点B的坐标为(4,0),
∴OC=AB=5,
∴点C的坐标为(0,5);
(2)设二次函数解析式为:y=ax2+bx+5,
把A(﹣1,0)、B(4,0)代入原函数解析式得出:
a=﹣,b=;
所以这个二次函数的解析式为:y=﹣x2+x+5.
点评:
此题主要考查了待定系数法求二次函数解析式,同时还考查了方程组的解法等知识.
18.已知抛物线的顶点坐标是(8,9),且过点(0,1),求该抛物线的解析式.
考点:
待定系数法求二次函数解析式.
分析:
根据抛物线的顶点坐标设出抛物线的解析式,再把(0,1),代入求解即可.
解答:
解:∵抛物线的顶点坐标是(8,9),
∴设抛物线的解析式为y=a(x﹣8)2+9,
把(0,1),代入得1=64a+9,解得a=﹣,
∴抛物线的解析式为y=﹣(x﹣8)2+9.
点评:
本题主要考查了用待定系数法求二次函数的解析式,解题的关键是正确的设出抛物线的解析式.
19.已知在直角坐标平面内,抛物线y=x2+bx+6经过x轴上两点A,B,点B的坐标为(3,0),与y轴相交于点C;
(1)求抛物线的表达式;
(2)求△ABC的面积.
考点:
待定系数法求二次函数解析式.
分析:
(1)把点B的坐标(3,0)代入抛物线y=x2+bx+6,即可得出抛物线的表达式y=x2﹣5x+6;
(2)先求出A(2,0),B(3,0),C(0,6),再利用三角形面积公式求解即可.
解答:
解:(1)把点B的坐标(3,0)代入抛物线y=x2+bx+6得0=9+3b+6,解得b=﹣5,
所以抛物线的表达式y=x2﹣5x+6;
(2)∵抛物线的表达式y=x2﹣5x+6;
∴A(2,0),B(3,0),C(0,6),
∴S△ABC=×1×6=3.
点评:
本题主要考查了用待定系数法求二次函数的解析式,解题的关键是正确的设出抛物线的解析式.
20.如图,已知二次函数的图象与x
( http: / / www.21cnjy.com )轴交于点A(1,0)和点B,与y轴交于点C(0,6),对称轴为直线x=2,求二次函数解析式并写出图象最低点坐标.
( http: / / www.21cnjy.com )
考点:
待定系数法求二次函数解析式;二次函数的最值.
专题:
计算题.
分析:
根据二次函数的对称轴为直线x=2,设
( http: / / www.21cnjy.com )出二次函数解析式,把A与C坐标代入求出a与k的值,确定出二次函数解析式,找出函数图象最低点坐标即可.
解答:
解:设二次函数解析式为y=a(x﹣2)2+k,
把A(1,0),C(0,6)代入得:,
解得:,
则二次函数解析式为y=2(x﹣2)2﹣2=2x2﹣8x+6,二次函数图象的最低点,即顶点坐标为(2,﹣2).
点评:
此题考查了待定系数法求二次函数解析式,以及二次函数的最值,熟练掌握待定系数法是解本题的关键.
21.如图,抛物线y=ax2+2x+c经过点A(0,3),B(﹣1,0),请解答下列问题:
(1)求抛物线的解析式;
(2)抛物线的顶点为点D,对称轴与x轴交于点E,连接BD,求BD的长.
注:抛物线y=ax2+bx+c(a≠0)的顶点坐标是(﹣,).
( http: / / www.21cnjy.com )
考点:
待定系数法求二次函数解析式;二次函数的性质.
专题:
计算题.
分析:
(1)将A与B代入抛物线解析式求出a与c的值,即可确定出抛物线解析式;
(2)利用顶点坐标公式表示
( http: / / www.21cnjy.com )出D点坐标,进而确定出E点坐标,得到DE与OE的长,根据B点坐标求出BO的长,进而求出BE的长,在直角三角形BED中,利用勾股定理求出BD的长.
解答:
解:(1)∵抛物线y=ax2+2x+c经过点A(0,3),B(﹣1,0),
∴将A与B坐标代入得:,
解得:,
则抛物线解析式为y=﹣x2+2x+3;
(2)点D为抛物线顶点,由顶点坐标(﹣,)得,D(1,4),
∵对称轴与x轴交于点E,
∴DE=4,OE=1,
∵B(﹣1,0),
∴BO=1,
∴BE=2,
在Rt△BED中,根据勾股定理得:BD===2.
点评:
此题考查了待定系数法求二次函数解析式,以及二次函数的性质,熟练掌握待定系数法是解本题的关键.
22.如图,抛物线y=ax2+bx﹣4a经过A(﹣1,0)、C(0,4)两点,与x轴交于另一点B.
(1)求抛物线的解析式;
(2)已知点D(m,m+1)在第一象限的抛物线上,求点D关于直线BC对称的点的坐标.
( http: / / www.21cnjy.com )
考点:
待定系数法求二次函数解析式;二次函数图象上点的坐标特征;坐标与图形变化-对称.
专题:
压轴题.
分析:
(1)由于抛物线y=ax2+bx﹣4a经过A(﹣1,0)、C(0,4)两点,利用待定系数法即可确定抛物线的解析式;
(2)由于点D(m,m+1)在第一象限的抛物线上,把D的坐标代入(1)中的解析式即可求出m,然后利用对称就可以求出关于直线BC对称的点的坐标.
解答:
解:(1)∵抛物线y=ax2+bx﹣4a经过A(﹣1,0)、C(0,4)两点,
∴,
解之得:a=﹣1,b=3,
∴y=﹣x2+3x+4;
(2)∵点D(m,m+1)在第一象限的抛物线上,
∴把D的坐标代入(1)中的解析式得
m+1=﹣m2+3m+4,
∴m=3或m=﹣1,
∴m=3,
∴D(3,4),
∵y=﹣x2+3x+4=0,x=﹣1或x=4,
∴B(4,0),
∴OB=OC,
∴△OBC是等腰直角三角形,
∴∠CBA=45°
设点D关于直线BC的对称点为点E
∵C(0,4)
∴CD∥AB,且CD=3
∴∠ECB=∠DCB=45°
∴E点在y轴上,且CE=CD=3
∴OE=1
∴E(0,1)
即点D关于直线BC对称的点的坐标为(0,1);
( http: / / www.21cnjy.com )
点评:
此题考查传统的待定系数求函数解析式,第二问考查点的对称问题,作合适的辅助线,根据垂直和三角形全等来求P点坐标
一.选择题(共8小题)
1.如果二次函数y=ax2+bx+c(a≠0)的图象如图所示,那么( )
( http: / / www.21cnjy.com )
A.a<0,b>0,c>0
B.a>0,b<0,c>0
C.a>0,b<0,c<0
D.a>0,b>0,c<0
2.如果二次函数y=ax2+bx+c的图象如图所示,那么下列判断正确的是( )
( http: / / www.21cnjy.com )
A.a>0,c>0
B.a<0,c>0
C.a>0,c<0
D.a<0,c<0
3.二次函数y=(a﹣1)x2(a为常数)的图象如图所示,则a的取值范围为( )
( http: / / www.21cnjy.com )
A.a>1
B.a<1
C.a>0
D.a<0
4.如果二次函数y=ax2+bx+c的图象如图所示,那么下列判断中,不正确的是( )
( http: / / www.21cnjy.com )
A.a>0
B.b>0
C.c<0
D.b2﹣4ac>0
5.抛物线y=(m﹣1)x2﹣mx﹣m2+1的图象过原点,则m的值为( )
A.±1
B.0
C.1
D.﹣1
6.(已知点(﹣2,4)在抛物线y=ax2上,则a的值是( )
A.﹣1
B.1
C.±1
D.
7.将二次函数y=x2的图象向下平移1个单位,再向右平移1个单位后所得图象的函数表达式为( )
A.y=(x+1)2+1
B.y=(x+1)2﹣1
C.y=(x﹣1)2+1
D.y=(x﹣1)2﹣1
8.将抛物线y=(x﹣1)2向左平移2个单位,所得抛物线的表达式为( )
A.y=(x+1)2
B.y=(x﹣3)2
C.y=(x﹣1)2+2
D.y=(x﹣1)2﹣2
二.填空题(共6小题)
9.已知抛物线经过点(5,﹣3),其对称轴为直线x=4,则抛物线一定经过另一点的坐标是 _________ .
10.如果二次函数y=(m﹣1)x2+5x+m2﹣1的图象经过原点,那么m= _________ .
11.若点(﹣2,a),(﹣3,b)都在
( http: / / www.21cnjy.com )二次函数y=x2+2x+m的图象上,比较a、b的大小:a _________ b.(填“>”“<”或“=”).
12.已知二次函数y=x2+2x﹣7的一个函数值是8,那么对应的自变量x的值是 _________ .
13.抛物线y=x2+2向左平移2个单位得到的抛物线表达式为 _________ .
14.如果将抛物线y=3x2平移,使平移后的抛物线顶点坐标为(2,2),那么平移后的抛物线的表达式为 _________ .
三.解答题(共8小题)
15.抛物线y=ax2+bx+c(a≠0)向右平移2个单位得到抛物线y=a(x﹣3)2﹣1,且平移后的抛物线经过点A(2,1).
(1)求平移后抛物线的解析式;
(2)设原抛物线与y轴的交点为B,顶点为P,平移后抛物线的对称轴与x轴交于点M,求△BPM的面积.
( http: / / www.21cnjy.com )
16.在直角坐标平面内,抛物线y=ax2+bx+c经过原点O、A(﹣2,﹣2)与B(1,﹣5)三点.
(1)求抛物线的表达式;
(2)写出该抛物线的顶点坐标.
17.如图,已知二次函数的图象过A、C、B三点,点A的坐标为(﹣1,0),点B的坐标为(4,0),点C在y轴正半轴上,且AB=OC.
(1)求点C的坐标;
(2)求二次函数的解析式,并化成一般形式.
( http: / / www.21cnjy.com )
18.已知抛物线的顶点坐标是(8,9),且过点(0,1),求该抛物线的解析式.
19.已知在直角坐标平面内,抛物线y=x2+bx+6经过x轴上两点A,B,点B的坐标为(3,0),与y轴相交于点C;
(1)求抛物线的表达式;
(2)求△ABC的面积.
20.如图,已知二次函数的图象与x轴交于点
( http: / / www.21cnjy.com )A(1,0)和点B,与y轴交于点C(0,6),对称轴为直线x=2,求二次函数解析式并写出图象最低点坐标.
( http: / / www.21cnjy.com )
21.如图,抛物线y=ax2+2x+c经过点A(0,3),B(﹣1,0),请解答下列问题:
(1)求抛物线的解析式;
(2)抛物线的顶点为点D,对称轴与x轴交于点E,连接BD,求BD的长.
注:抛物线y=ax2+bx+c(a≠0)的顶点坐标是(﹣,).
( http: / / www.21cnjy.com )
22.如图,抛物线y=ax2+bx﹣4a经过A(﹣1,0)、C(0,4)两点,与x轴交于另一点B.
(1)求抛物线的解析式;
(2)已知点D(m,m+1)在第一象限的抛物线上,求点D关于直线BC对称的点的坐标.
( http: / / www.21cnjy.com )
26.2.3求二次函数关系式
参考答案与试题解析
一.选择题(共8小题)
1.如果二次函数y=ax2+bx+c(a≠0)的图象如图所示,那么( )
( http: / / www.21cnjy.com )
A.
a<0,b>0,c>0
B.a>0,b<0,c>0
C.a>0,b<0,c<0
D.
a>0,b>0,c<0
考点:
二次函数图象与系数的关系.
分析:
首先根据开口方向确定a的符号,再依据对称轴的正负和a的符号即可判断b的符号,然后根据与y轴的交点的纵坐标即可判断c的正负,由此得出答案即可.
解答:
解:∵图象开口方向向上,
∴a>0;
∵图象的对称轴在x轴的正半轴上,
∴﹣>0,
∵a>0,
∴b<0;
∵图象与Y轴交点在y轴的负半轴上,
∴c<0;
∴a>0,b<0,c<0.
故选:C.
点评:
本题主要考查二次函数的图象与系数的关系,能根据图象正确确定各个系数的符号是解决此题的关键,运用了数形结合思想.
2.如果二次函数y=ax2+bx+c的图象如图所示,那么下列判断正确的是( )
( http: / / www.21cnjy.com )
A.
a>0,c>0
B.a<0,c>0
C.a>0,c<0
D.
a<0,c<0
考点:
二次函数图象与系数的关系.
分析:
首先根据开口方向确定a的符号,再依据与y轴的交点的纵坐标即可判断c的正负,由此解决问题.
解答:
解:∵图象开口方向向上,
∴a>0;
∵图象与Y轴交点在y轴的负半轴上,
∴c<0;
∴a>0,c<0.
故选:C.
点评:
本题主要考查二次函数的图象与系数的关系,能根据图象正确确定各个系数的符号是解决此题的关键,运用了数形结合思想.
3.二次函数y=(a﹣1)x2(a为常数)的图象如图所示,则a的取值范围为( )
( http: / / www.21cnjy.com )
A.
a>1
B.a<1
C.a>0
D.
a<0
考点:
二次函数图象与系数的关系.
分析:
由图示知,该抛物线的开口方向向下,则系数a﹣1<0,据此可求a的取值范围.
解答:
解:如图,
( http: / / www.21cnjy.com )
抛物线的开口方向向下,则a﹣1<0,
解得a<1.
故选:B.
点评:
本题考查了二次函数的图象与系数的关
( http: / / www.21cnjy.com )系.二次函数y=ax2的系数a为正数时,抛物线开口向上;a为负数时,抛物线开口向下;a的绝对值越大,抛物线开口越小.
4.如果二次函数y=ax2+bx+c的图象如图所示,那么下列判断中,不正确的是( )
( http: / / www.21cnjy.com )
A.
a>0
B.b>0
C.c<0
D.
b2﹣4ac>0
考点:
二次函数图象与系数的关系.
分析:
首先根据开口方向确
( http: / / www.21cnjy.com )定a的符号,再依据对称轴的正负和a的符号即可判断b的符号,然后根据与y轴的交点的纵坐标即可判断c的正负,由二次函数y=ax2+bx+c的图象与x轴有两个交点,可得b2﹣4ac>0.
解答:
解:由图象的开口向上可得a开口向上,由x=﹣>0,可得b<0,
由二次函数y=ax2+bx+c的图象交y轴于负半轴可得c<0,
由二次函数y=ax2+bx+c的图象与x轴有两个交点,可得b2﹣4ac>0,所以B不正确.
故选:B.
点评:
本题主要考查二次函数的图象与系数的关系,能根据图象正确确定各个系数的符号是解决此题的关键,此题运用了数形结合思想.
5.抛物线y=(m﹣1)x2﹣mx﹣m2+1的图象过原点,则m的值为( )
A.
±1
B.0
C.1
D.
﹣1
考点:
二次函数图象上点的坐标特征;二次函数的定义.
专题:
计算题.
分析:
根据二次函数图象上点的坐标特征得到﹣m2+1=0,解得m1=1,m2=﹣1,然后根据二次函数的定义确定m的值.
解答:
解:把(0,0)代入y=(m﹣1)x2﹣mx﹣m2+1得﹣m2+1=0,解得m1=1,m2=﹣1,
而m﹣1≠0,
所以m=﹣1.
故选D.
点评:
本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.也考查了二次函数的定义.
6.已知点(﹣2,4)在抛物线y=ax2上,则a的值是( )
A.
﹣1
B.1
C.±1
D.
考点:
二次函数图象上点的坐标特征.
专题:
计算题.
分析:
根据二次函数图象上点的坐标特征,把点(﹣2,4)代入y=ax2中得到a的方程,然后解方程即可.
解答:
解:∵点(﹣2,4)在抛物线y=ax2上,
∴a (﹣2)2=4,
∴a=1.
故选B.
点评:
本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.
7.将二次函数y=x2的图象向下平移1个单位,再向右平移1个单位后所得图象的函数表达式为( )
A.
y=(x+1)2+1
B.y=(x+1)2﹣1
C.y=(x﹣1)2+1
D.
y=(x﹣1)2﹣1
考点:
二次函数图象与几何变换.
分析:
先得到抛物线y=x2的顶点坐标
( http: / / www.21cnjy.com )为(0,0),再利用点的平移规律得到点(0,0)平移后对应点的坐标为(1,﹣1),然后根据顶点式写出平移的抛物线解析式.
解答:
解:抛物线y=x2的顶点坐标为(0,0),把点(0,0)向右平移1个单位,向下平移1个单位得到对应点的坐标为(1,﹣1),所以平移后的新图象的函数表达式为y=(x﹣1)2﹣1.
故选:D.
点评:
本题考查了二次函数图象上点的坐标特征:由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.
8.将抛物线y=(x﹣1)2向左平移2个单位,所得抛物线的表达式为( )
A.
y=(x+1)2
B.y=(x﹣3)2
C.y=(x﹣1)2+2
D.
y=(x﹣1)2﹣2
考点:
二次函数图象与几何变换.
专题:
几何变换.
分析:
先根据二次函数的性质得到抛
( http: / / www.21cnjy.com )物线y=(x﹣1)2的顶点坐标为(1,0),再利用点平移的规律得到点(1,0)平移后对应点的坐标为(﹣1,0),然后根据顶点式写出平移后抛物线的表达式.
解答:
解:抛物线y=(x﹣1)2的顶点坐标为(1,0),点(1,0)向左平移2个单位得到对应点的坐标为(﹣1,0),所以平移后抛物线的表达式为y=(x+1)2.
故选A.
点评:
本题考查了二次函数图象与几何变换:由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.
二.填空题(共6小题)
9.已知抛物线经过点(5,﹣3),其对称轴为直线x=4,则抛物线一定经过另一点的坐标是 (3,﹣3) .
考点:
二次函数图象上点的坐标特征.
分析:
根据二次函数的对称性求解即可.
解答:
解:∵点(5,﹣3)关于对称轴直线x=4的对称点为(3,﹣3),
∴抛物线一定经过另一点的坐标是(3,﹣3).
故答案为:(3,﹣3).
点评:
本题考查了二次函数图象上点的坐标特征,主要利用了二次函数的对称性.
10.如果二次函数y=(m﹣1)x2+5x+m2﹣1的图象经过原点,那么m= ﹣1 .
考点:
二次函数图象上点的坐标特征;二次函数的定义.
分析:
把原点坐标代入函数解析式求解即可得到m的值,再根据二次项系数不等于0求出m≠1.
解答:
解:∵二次函数y=(m﹣1)x2+5x+m2﹣1的图象经过原点,
∴m2﹣1=0,
解得m=±1,
∵函数为二次函数,
∴m﹣1≠0,
解得m≠1,
所以,m=﹣1.
故答案为:﹣1.
点评:
本题考查了二次函数图象上点的坐标特征,二次函数的定义,要注意二次项系数不等于0.
11.若点(﹣2,a),(﹣3,b)都在二次函数y=x2+2x+m的图象上,比较a、b的大小:a < b.(填“>”“<”或“=”).
考点:
二次函数图象上点的坐标特征.
分析:
根据二次函数图象上点的坐标特征计算出自变量为﹣2和﹣3时的函数值,然后比较函数值的大小即可.
解答:
解:∵点(﹣2,a),(﹣3,b)都在二次函数y=x2+2x+m的图象,
∴a=x2+2x+m=4﹣4+m=4,b=x2+2x+m=9﹣6+m=3+m,
∴a<b.
故答案为<.
点评:
本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.
12.已知二次函数y=x2+2x﹣7的一个函数值是8,那么对应的自变量x的值是 ﹣5或3 .
考点:
二次函数图象上点的坐标特征.
分析:
把函数值代入函数解析式,解关于x的一元二次方程即可.
解答:
解:y=8时,x2+2x﹣7=8,
整理得,x2+2x﹣15=0,
解得x1=﹣5,x2=3,
所以,对应的自变量x的值是﹣5或3.
故答案为:﹣5或3.
点评:
本题考查了二次函数图象上点的坐标特征,一元二次方程的解法,把函数值代入函数解析式得到方程是解题的关键.
13.抛物线y=x2+2向左平移2个单位得到的抛物线表达式为 y=(x+2)2+2 .
考点:
二次函数图象与几何变换.
分析:
已知抛物线解析式为顶点式,顶点坐标为(0,2),则平移后顶点坐标为(﹣2,2),由抛物线的顶点式可求平移后的抛物线解析式.
解答:
解:∵y=x2+2顶点坐标为(0,2),
∴向左平移2个单位后顶点坐标为(﹣2,2),
∴所得新抛物线的表达式为y=(x+2)2+2.
故答案为:y=(x+2)2+2.
点评:
本题考查了二次函数图象与几何变换.关键是把抛物线的平移理解为顶点的平移,根据顶点式求抛物线解析式.
14.如果将抛物线y=3x2平移,使平移后的抛物线顶点坐标为(2,2),那么平移后的抛物线的表达式为 y=3(x﹣2)2+2 .
考点:
二次函数图象与几何变换.
分析:
平移不改变抛物线的开口方向与开口大小,即解析式的二次项系数不变,根据抛物线的顶点式可求抛物线解析式.
解答:
解:∵原抛物线解析式为y=3x2,的顶点坐标是(0,0),平移后抛物线顶点坐标为(2,2),
∴平移后的抛物线的表达式为:y=3(x﹣2)2+2.
故答案为:y=3(x﹣2)2+2.
点评:
本题考查了抛物线的平移与解析式变化的关系.关键是明确抛物线的平移实质上是顶点的平移,能用顶点式表示平移后的抛物线解析式.
三.解答题(共8小题)
15.抛物线y=ax2+bx+c(a≠0)向右平移2个单位得到抛物线y=a(x﹣3)2﹣1,且平移后的抛物线经过点A(2,1).
(1)求平移后抛物线的解析式;
(2)设原抛物线与y轴的交点为B,顶点为P,平移后抛物线的对称轴与x轴交于点M,求△BPM的面积.
( http: / / www.21cnjy.com )
考点:
二次函数图象与几何变换.
分析:
(1)把点A代入平移后的抛物线y=a(x﹣3)2﹣1来求a的值;
(2)根据平移前、后的函数解析式,然后求出B、P、M三点的坐标,根据三角形的面积公式即可求出△BPM的面积.
解答:
解:(1)把点A(2,1)代入y=a(x﹣3)2﹣1,得
1=a(2﹣3)2﹣1,
整理,得
1=a﹣1,
解得
a=2.
则平移后的抛物线解析式为:y=2(x﹣3)2﹣1;
(2)由(1)知,平移后的抛物线解析式为:y=2(x﹣3)2﹣1,则M(3,0)
∵抛物线y=ax2+bx+c(a≠0)向右平移2个单位得到抛物线y=2(x﹣3)2﹣1,
∴平移前的抛物线解析式为:y=2(x﹣1)2﹣1.
∴P(1,﹣1).
令x=0,则y=1.
故B(0,1),
∴BM=
∴S△BPM=BM yP=××1=.
( http: / / www.21cnjy.com )
点评:
本题主要考查了二次函数解析式的确定、图形的面积求法、函数图象交点等知识及综合应用知识、解决问题的能力.
16.在直角坐标平面内,抛物线y=ax2+bx+c经过原点O、A(﹣2,﹣2)与B(1,﹣5)三点.
(1)求抛物线的表达式;
(2)写出该抛物线的顶点坐标.
考点:
待定系数法求二次函数解析式;二次函数的性质.
分析:
(1)把原点O、A(﹣2,﹣2)与B(1,﹣5)三点分别代入函数解析式,求得a、b、c的数值得出函数解析式即可;
(2)把函数解析式化为顶点式,得出顶点坐标即可.
解答:
解:(1)∵抛物线y=ax2+bx+c经过原点O、A(﹣2,﹣2)与B(1,﹣5)三点,
∴,
解得:,
∴抛物线的表达式为y=﹣2x2﹣3x.
(2)y=﹣2x2﹣3x
=y=﹣2(x+)2+,
抛物线的顶点坐标为(﹣,).
点评:
此题考查待定系数法求函数解析式,以及利用配方法求得顶点坐标.
17.如图,已知二次函数的图象过A、C、B三点,点A的坐标为(﹣1,0),点B的坐标为(4,0),点C在y轴正半轴上,且AB=OC.
(1)求点C的坐标;
(2)求二次函数的解析式,并化成一般形式.
( http: / / www.21cnjy.com )
考点:
待定系数法求二次函数解析式.
分析:
(1)根据题目所给的信息可以知道OC=AB=5,点C在y轴上可以写出点C的坐标;
(2)二次函数图象经过点A、B、C;这三个点的坐标已知,根据三点法确定这一二次函数解析式.
解答:
解:(1)∵点A的坐标为(﹣1,0),点B的坐标为(4,0),
∴OC=AB=5,
∴点C的坐标为(0,5);
(2)设二次函数解析式为:y=ax2+bx+5,
把A(﹣1,0)、B(4,0)代入原函数解析式得出:
a=﹣,b=;
所以这个二次函数的解析式为:y=﹣x2+x+5.
点评:
此题主要考查了待定系数法求二次函数解析式,同时还考查了方程组的解法等知识.
18.已知抛物线的顶点坐标是(8,9),且过点(0,1),求该抛物线的解析式.
考点:
待定系数法求二次函数解析式.
分析:
根据抛物线的顶点坐标设出抛物线的解析式,再把(0,1),代入求解即可.
解答:
解:∵抛物线的顶点坐标是(8,9),
∴设抛物线的解析式为y=a(x﹣8)2+9,
把(0,1),代入得1=64a+9,解得a=﹣,
∴抛物线的解析式为y=﹣(x﹣8)2+9.
点评:
本题主要考查了用待定系数法求二次函数的解析式,解题的关键是正确的设出抛物线的解析式.
19.已知在直角坐标平面内,抛物线y=x2+bx+6经过x轴上两点A,B,点B的坐标为(3,0),与y轴相交于点C;
(1)求抛物线的表达式;
(2)求△ABC的面积.
考点:
待定系数法求二次函数解析式.
分析:
(1)把点B的坐标(3,0)代入抛物线y=x2+bx+6,即可得出抛物线的表达式y=x2﹣5x+6;
(2)先求出A(2,0),B(3,0),C(0,6),再利用三角形面积公式求解即可.
解答:
解:(1)把点B的坐标(3,0)代入抛物线y=x2+bx+6得0=9+3b+6,解得b=﹣5,
所以抛物线的表达式y=x2﹣5x+6;
(2)∵抛物线的表达式y=x2﹣5x+6;
∴A(2,0),B(3,0),C(0,6),
∴S△ABC=×1×6=3.
点评:
本题主要考查了用待定系数法求二次函数的解析式,解题的关键是正确的设出抛物线的解析式.
20.如图,已知二次函数的图象与x
( http: / / www.21cnjy.com )轴交于点A(1,0)和点B,与y轴交于点C(0,6),对称轴为直线x=2,求二次函数解析式并写出图象最低点坐标.
( http: / / www.21cnjy.com )
考点:
待定系数法求二次函数解析式;二次函数的最值.
专题:
计算题.
分析:
根据二次函数的对称轴为直线x=2,设
( http: / / www.21cnjy.com )出二次函数解析式,把A与C坐标代入求出a与k的值,确定出二次函数解析式,找出函数图象最低点坐标即可.
解答:
解:设二次函数解析式为y=a(x﹣2)2+k,
把A(1,0),C(0,6)代入得:,
解得:,
则二次函数解析式为y=2(x﹣2)2﹣2=2x2﹣8x+6,二次函数图象的最低点,即顶点坐标为(2,﹣2).
点评:
此题考查了待定系数法求二次函数解析式,以及二次函数的最值,熟练掌握待定系数法是解本题的关键.
21.如图,抛物线y=ax2+2x+c经过点A(0,3),B(﹣1,0),请解答下列问题:
(1)求抛物线的解析式;
(2)抛物线的顶点为点D,对称轴与x轴交于点E,连接BD,求BD的长.
注:抛物线y=ax2+bx+c(a≠0)的顶点坐标是(﹣,).
( http: / / www.21cnjy.com )
考点:
待定系数法求二次函数解析式;二次函数的性质.
专题:
计算题.
分析:
(1)将A与B代入抛物线解析式求出a与c的值,即可确定出抛物线解析式;
(2)利用顶点坐标公式表示
( http: / / www.21cnjy.com )出D点坐标,进而确定出E点坐标,得到DE与OE的长,根据B点坐标求出BO的长,进而求出BE的长,在直角三角形BED中,利用勾股定理求出BD的长.
解答:
解:(1)∵抛物线y=ax2+2x+c经过点A(0,3),B(﹣1,0),
∴将A与B坐标代入得:,
解得:,
则抛物线解析式为y=﹣x2+2x+3;
(2)点D为抛物线顶点,由顶点坐标(﹣,)得,D(1,4),
∵对称轴与x轴交于点E,
∴DE=4,OE=1,
∵B(﹣1,0),
∴BO=1,
∴BE=2,
在Rt△BED中,根据勾股定理得:BD===2.
点评:
此题考查了待定系数法求二次函数解析式,以及二次函数的性质,熟练掌握待定系数法是解本题的关键.
22.如图,抛物线y=ax2+bx﹣4a经过A(﹣1,0)、C(0,4)两点,与x轴交于另一点B.
(1)求抛物线的解析式;
(2)已知点D(m,m+1)在第一象限的抛物线上,求点D关于直线BC对称的点的坐标.
( http: / / www.21cnjy.com )
考点:
待定系数法求二次函数解析式;二次函数图象上点的坐标特征;坐标与图形变化-对称.
专题:
压轴题.
分析:
(1)由于抛物线y=ax2+bx﹣4a经过A(﹣1,0)、C(0,4)两点,利用待定系数法即可确定抛物线的解析式;
(2)由于点D(m,m+1)在第一象限的抛物线上,把D的坐标代入(1)中的解析式即可求出m,然后利用对称就可以求出关于直线BC对称的点的坐标.
解答:
解:(1)∵抛物线y=ax2+bx﹣4a经过A(﹣1,0)、C(0,4)两点,
∴,
解之得:a=﹣1,b=3,
∴y=﹣x2+3x+4;
(2)∵点D(m,m+1)在第一象限的抛物线上,
∴把D的坐标代入(1)中的解析式得
m+1=﹣m2+3m+4,
∴m=3或m=﹣1,
∴m=3,
∴D(3,4),
∵y=﹣x2+3x+4=0,x=﹣1或x=4,
∴B(4,0),
∴OB=OC,
∴△OBC是等腰直角三角形,
∴∠CBA=45°
设点D关于直线BC的对称点为点E
∵C(0,4)
∴CD∥AB,且CD=3
∴∠ECB=∠DCB=45°
∴E点在y轴上,且CE=CD=3
∴OE=1
∴E(0,1)
即点D关于直线BC对称的点的坐标为(0,1);
( http: / / www.21cnjy.com )
点评:
此题考查传统的待定系数求函数解析式,第二问考查点的对称问题,作合适的辅助线,根据垂直和三角形全等来求P点坐标
