8.2.1 二元一次方程组的解法---代入消元法 课件
文档属性
| 名称 | 8.2.1 二元一次方程组的解法---代入消元法 课件 |  | |
| 格式 | zip | ||
| 文件大小 | 331.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-11-06 20:24:31 | ||
图片预览








文档简介
课件21张PPT。8.2 消元——解二元一次方程组
(第一课时)知之者不如好之者,
好之者不如乐之者。态度决定一切,现在决定将来。温故而知新二元一次方程有无数多个解2、x=5 y=3是方x+y=8的解吗? 所以 方程组 x+y=85x+3y=34的解是x= 5y= 3它是方程5x+3y=34的解吗?1、什么叫二元一次方程组的解?探究新知 你能根据问题中的等量关系列出二元一次方程组吗?问题 篮球联赛中,每场都要分出胜负,每队胜1场得2分,负1场得1分.某队10场比赛中得到16分,那么这个队胜负场数分别是多少?这个实际问题还可以根据等量关系列一元一次方程吗?探究新知解:设胜x场,则负(10-x)场.根据题意得:
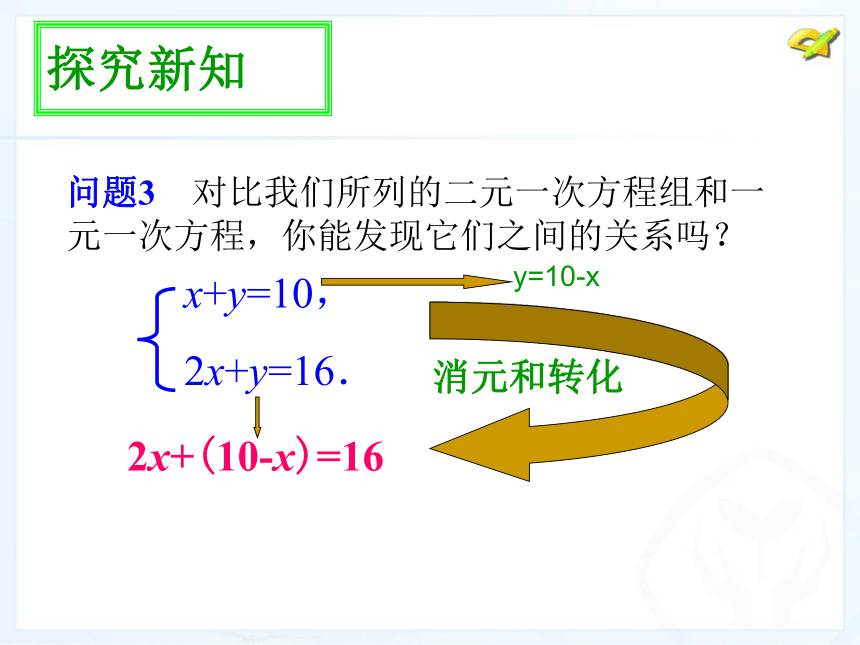
2x+(10-x)=16.问题 篮球联赛中,每场都要分出胜负,每队胜1场得2分,负1场得1分.某队10场比赛中得到16分,那么这个队胜负场数分别是多少?探究新知问题3 对比我们所列的二元一次方程组和一元一次方程,你能发现它们之间的关系吗?2x+(10-x)=16消元和转化y=10-x知识点一消元思想 1、在方程组 中:
把方程x+y=10 ,写成y=10-x,把2x+y=16中的y换为10-x,得一元一次方程__________=16,
解得x=6,把x=6代入_____________,得y=4.从而得到这个方程组的解.
归纳: 这种将未知数的个数由多化少、逐一解决的思想,叫做_________思想.
2x+(10-x) y=10-x消元探究新知 把二元一次方程组中一个方程的一个未知数用含另一个未知数的式子表示出来,再代入另一个方程,实现消元,进而求得这个二元一次方程组的解.这种方法叫做代入消元法,简称代入法.知识点二探究新知由①,得 把③代入②,得 把 x=6 代入③,得 ∴这个方程组的解是答:这个队胜6场、负4场. 你能用刚才的分析解二元一次方程组吗?步骤怎么写?这个队到底胜了几场?负了几场?解:设:这个对胜x场,负y场.据题意可列方程组为:③三、教学关键 1、把x+y=10 ,写成y=________,叫做用x含的式子表示y的形式;把 x+y=10,写成x=__________,叫做用含y的式子表示x的形式。
10-x10-y知识点三 方程变形新知应用 例1:已知方程x-2y=4,先用含x的代数式
表示y,再用含y的代数式表示x,并比较
哪一种形式比较简便。
例1 用代入法解方程组 例题精讲x – y = 3①3x - 8y =14②二
元
一
次
方
程
组x-y=33x-8y=14y=-1x = 2解得y变形解得x代入消x一元一次方程
3(y+3)-8y=14.x =y+3.用y+3代替x,消未知数x.探索方法①
②
例1 用代入法解方程组
分析:方程①中x的系数是____,
用含____的式子表示x,比较简便.
解:由①得:x= … ③
把③代入②得:3( ___)- __= ___
解这个方程得:y= ___.
把y= _代入③得:x= __
∴原方程组的解是1yy+3 y+3 8y 14-1-12-12方法总结解二元一次方程组的一般步骤变形选择一个未知数系数比较简单的方程,用含有一个未知数的式子表示另一个未知数。代入将变形的方程代入到另一个方程,进行等量替换,实现消元的目的。将二元一次方程组转化为一元一次方程。求解解这个一元一次方程,将所求的一元一次方程的解代入到所变形的方程中,求得另一个未知数的值写解写出原二元一次方程组的解练习提高,形成能力练习: 1.把下列方程改写成用含 的式子表示 的形式:⑴ ⑵ ;. 2.用代入法解下列方组:⑴ ⑵ 2、 用代入法解下列方程组:①
②
(1)
解:把①代入②,得
3x+2( )=_
解这个方程,得x= __ .
把x= 代入①,得y= __
∴原方程组的解是2x-3822211 用代入法解下列方程组: (2) ①
② 解:由①,得y=2x-5… ③
把③代入②,得3x+4(2x-5)= 2
解这个方程,得x=2
把x=2代入③,得y=-1
∴原方程组的解是2-1小结1、解二元一次方程组的基本思想是什么?基本思想:消元: 二元一元2、用代入法解方程组的步骤是什么?主要步骤: 变形用含一个未知数的代数式
表示另一个未知数代入消去一个元(未知数)求解分别求出两个未知数的值写解写出方程组的解3、在探究解法的过程中用到了什么思想?你还有 哪些收获?(转化的数学思想)作业设计1.(必做题)教材P97页习题8.2复习巩固第1、(1)(2)题、第2题(1)(2)题。
2.(选做题) 教材P97页习题8.2复习巩固第1、(3)(4)题、第2题(3)(4)。
(第一课时)知之者不如好之者,
好之者不如乐之者。态度决定一切,现在决定将来。温故而知新二元一次方程有无数多个解2、x=5 y=3是方x+y=8的解吗? 所以 方程组 x+y=85x+3y=34的解是x= 5y= 3它是方程5x+3y=34的解吗?1、什么叫二元一次方程组的解?探究新知 你能根据问题中的等量关系列出二元一次方程组吗?问题 篮球联赛中,每场都要分出胜负,每队胜1场得2分,负1场得1分.某队10场比赛中得到16分,那么这个队胜负场数分别是多少?这个实际问题还可以根据等量关系列一元一次方程吗?探究新知解:设胜x场,则负(10-x)场.根据题意得:
2x+(10-x)=16.问题 篮球联赛中,每场都要分出胜负,每队胜1场得2分,负1场得1分.某队10场比赛中得到16分,那么这个队胜负场数分别是多少?探究新知问题3 对比我们所列的二元一次方程组和一元一次方程,你能发现它们之间的关系吗?2x+(10-x)=16消元和转化y=10-x知识点一消元思想 1、在方程组 中:
把方程x+y=10 ,写成y=10-x,把2x+y=16中的y换为10-x,得一元一次方程__________=16,
解得x=6,把x=6代入_____________,得y=4.从而得到这个方程组的解.
归纳: 这种将未知数的个数由多化少、逐一解决的思想,叫做_________思想.
2x+(10-x) y=10-x消元探究新知 把二元一次方程组中一个方程的一个未知数用含另一个未知数的式子表示出来,再代入另一个方程,实现消元,进而求得这个二元一次方程组的解.这种方法叫做代入消元法,简称代入法.知识点二探究新知由①,得 把③代入②,得 把 x=6 代入③,得 ∴这个方程组的解是答:这个队胜6场、负4场. 你能用刚才的分析解二元一次方程组吗?步骤怎么写?这个队到底胜了几场?负了几场?解:设:这个对胜x场,负y场.据题意可列方程组为:③三、教学关键 1、把x+y=10 ,写成y=________,叫做用x含的式子表示y的形式;把 x+y=10,写成x=__________,叫做用含y的式子表示x的形式。
10-x10-y知识点三 方程变形新知应用 例1:已知方程x-2y=4,先用含x的代数式
表示y,再用含y的代数式表示x,并比较
哪一种形式比较简便。
例1 用代入法解方程组 例题精讲x – y = 3①3x - 8y =14②二
元
一
次
方
程
组x-y=33x-8y=14y=-1x = 2解得y变形解得x代入消x一元一次方程
3(y+3)-8y=14.x =y+3.用y+3代替x,消未知数x.探索方法①
②
例1 用代入法解方程组
分析:方程①中x的系数是____,
用含____的式子表示x,比较简便.
解:由①得:x= … ③
把③代入②得:3( ___)- __= ___
解这个方程得:y= ___.
把y= _代入③得:x= __
∴原方程组的解是1yy+3 y+3 8y 14-1-12-12方法总结解二元一次方程组的一般步骤变形选择一个未知数系数比较简单的方程,用含有一个未知数的式子表示另一个未知数。代入将变形的方程代入到另一个方程,进行等量替换,实现消元的目的。将二元一次方程组转化为一元一次方程。求解解这个一元一次方程,将所求的一元一次方程的解代入到所变形的方程中,求得另一个未知数的值写解写出原二元一次方程组的解练习提高,形成能力练习: 1.把下列方程改写成用含 的式子表示 的形式:⑴ ⑵ ;. 2.用代入法解下列方组:⑴ ⑵ 2、 用代入法解下列方程组:①
②
(1)
解:把①代入②,得
3x+2( )=_
解这个方程,得x= __ .
把x= 代入①,得y= __
∴原方程组的解是2x-3822211 用代入法解下列方程组: (2) ①
② 解:由①,得y=2x-5… ③
把③代入②,得3x+4(2x-5)= 2
解这个方程,得x=2
把x=2代入③,得y=-1
∴原方程组的解是2-1小结1、解二元一次方程组的基本思想是什么?基本思想:消元: 二元一元2、用代入法解方程组的步骤是什么?主要步骤: 变形用含一个未知数的代数式
表示另一个未知数代入消去一个元(未知数)求解分别求出两个未知数的值写解写出方程组的解3、在探究解法的过程中用到了什么思想?你还有 哪些收获?(转化的数学思想)作业设计1.(必做题)教材P97页习题8.2复习巩固第1、(1)(2)题、第2题(1)(2)题。
2.(选做题) 教材P97页习题8.2复习巩固第1、(3)(4)题、第2题(3)(4)。
