华师大版九年级数学下27.1.1圆的基本元素同步练习(解析版)
文档属性
| 名称 | 华师大版九年级数学下27.1.1圆的基本元素同步练习(解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 227.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-11-06 23:52:16 | ||
图片预览


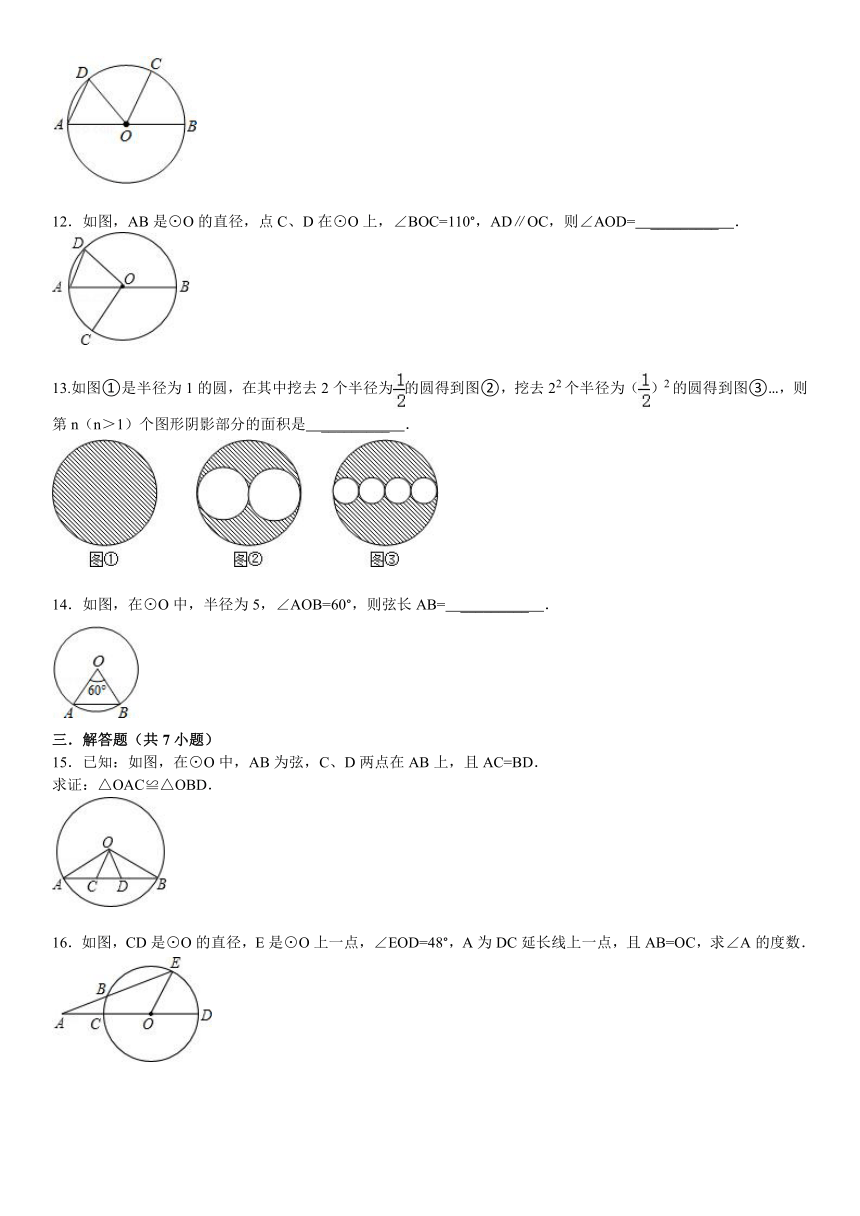


文档简介
27.1.1圆的基本元素
农安县合隆中学
徐亚惠
一.选择题(共8小题)
1.如图,一个小圆沿着一个五边形的边滚动,如果五边形的各边长都和小圆的周长相等,那么当小圆滚动到原来位置时,小圆自身滚动的圈数是( )
( http: / / www.21cnjy.com )
A.4
B.5
C.6
D.10
2.下列说法中,结论错误的是( )
A.直径相等的两个圆是等圆
B.长度相等的两条弧是等弧
C.圆中最长的弦是直径
D.一条弦把圆分成两条弧,这两条弧可能是等弧
3.如图,AB是⊙O的直径,点C、D在⊙
( http: / / www.21cnjy.com )O上,且点C、D在AB的异侧,连结AD、OD、OC.若∠AOC=70°,且AD∥OC,则∠AOD的度数为( )
( http: / / www.21cnjy.com )
A.70°
B.60°
C.50°
D.40°
4.如图,弧AD是以等边三角形ABC一边AB为半径的四分之一圆周,P为弧AD上任意一点,若AC=5,则四边形ACBP周长的最大值是( )
( http: / / www.21cnjy.com )
A.15
B.15+5
C.20
D.15+5
5.如图,在半圆的直径上作4个正三角形,如这半圆周长为C1,这4个正三角形的周长和为C2,则C1和C2的大小关系是( )
A.C1>C2
B.C1<C2
C.C1=C2
D.不能确定
6.在△ABC中,∠C为锐角,分别以AB,AC为直径作半圆,过点B,A,C作,如图所示.若AB=4,AC=2,S1﹣S2=,则S3﹣S4的值是( )
( http: / / www.21cnjy.com )
A.
B.
C.
D.
7.车轮要做成圆形,实际上就是根据圆的特征( )
A.同弧所对的圆周角相等
B.直径是圆中最大的弦
C.圆上各点到圆心的距离相等
D.圆是中心对称图形
8.如图,以坐标原点O为圆心的圆与y轴交于点A、B,且OA=1,则点B的坐标是( )
( http: / / www.21cnjy.com )
A.(0,1)
B.(0,﹣1)
C.(
1,0)
D.(﹣1,0)
二.填空题(共6小题)
9.如图,以△ABC的边BC为直径的⊙O分别交AB、AC于点D、E,连结OD、OE,若∠A=65°,则∠DOE= _________ .
( http: / / www.21cnjy.com )
10.如图,以AB为直径的半圆O上有两点D
( http: / / www.21cnjy.com )、E,ED与BA的延长线交于点C,且有DC=OE,若∠C=20°,则∠EOB的度数是 _________ .
( http: / / www.21cnjy.com )
11.如图,AB为⊙O直径,点C、D在⊙O上,已知∠AOD=50°,AD∥OC,则∠BOC= _________ 度.
( http: / / www.21cnjy.com )
12.如图,AB是⊙O的直径,点C、D在⊙O上,∠BOC=110°,AD∥OC,则∠AOD= _________ .
( http: / / www.21cnjy.com )
13.如图①是半径为1的圆,在其中挖去2个半径为的圆得到图②,挖去22个半径为()2的圆得到图③…,则第n(n>1)个图形阴影部分的面积是 _________ .
( http: / / www.21cnjy.com )
14.如图,在⊙O中,半径为5,∠AOB=60°,则弦长AB= _________ .
( http: / / www.21cnjy.com )
三.解答题(共7小题)
15.已知:如图,在⊙O中,AB为弦,C、D两点在AB上,且AC=BD.
求证:△OAC≌△OBD.
( http: / / www.21cnjy.com )
16.如图,CD是⊙O的直径,E是⊙O上一点,∠EOD=48°,A为DC延长线上一点,且AB=OC,求∠A的度数.
( http: / / www.21cnjy.com )
17.如图所示,AB为⊙O的直径,CD是⊙O的弦,AB、CD的延长线交于点E,已知AB=2DE,∠AEC=20°.求∠AOC的度数.
( http: / / www.21cnjy.com )
18.如图,点O是同心圆的圆心,大圆半径OA,OB分别交小圆于点C,D,求证:AB∥CD.
( http: / / www.21cnjy.com )
19.已知AB为⊙O的弦,C、D在AB上,且AC=CD=DB,求证:∠AOC=∠DOB.
( http: / / www.21cnjy.com )
20.如图,AB是半圆O的直径,D是半圆上的一点,∠DOB=75°,DC交BA延长线于E,交半圆于C,且CE=AO,求∠E的度数.
( http: / / www.21cnjy.com )
21.如图,点B是线段AC上的一点,分别以AB、BC、CA为直径作半圆,求证:半圆AB的长与半圆BC的长之和等于半圆AC的长.
( http: / / www.21cnjy.com )
27.1.1圆的基本元素
参考答案与试题解析
一.选择题(共8小题)
1.如图,一个小圆沿着一个五边形的边滚动,如果五边形的各边长都和小圆的周长相等,那么当小圆滚动到原来位置时,小圆自身滚动的圈数是( )
( http: / / www.21cnjy.com )
A.
4
B.5
C.6
D.
10
考点:
圆的认识;多边形内角与外角.
专题:
压轴题.
分析:
因为五边形的各边长都和小圆的周长相
( http: / / www.21cnjy.com )等,所有小圆在每一边上滚动正好一周,另外五边形的外角和为360°,所有小圆在五个角处共滚动一周,可以求出小圆滚动的圈数.
解答:
解:因为五边形的各
( http: / / www.21cnjy.com )边长都和小圆的周长相等,所有小圆在每一边上滚动正好一周,在五条边上共滚动了5周.由于每次小圆从五边形的一边滚动到另一边时,都会翻转72°,所以小圆在五个角处共滚动一周.因此,总共是滚动了6周.
故选:C.
点评:
本题考查的是对圆的认识,根据圆的周长与五边形的边长相等,可以知道圆在每边上滚动一周.然后由多边形外角和是360°,可以知道圆在五个角处滚动一周.因此可以求出滚动的总圈数.
2.下列说法中,结论错误的是( )
A.
直径相等的两个圆是等圆
B.
长度相等的两条弧是等弧
C.
圆中最长的弦是直径
D.
一条弦把圆分成两条弧,这两条弧可能是等弧
考点:
圆的认识.
分析:
利用圆的有关定义进行判断后利用排除法即可得到正确的答案;
解答:
解:A、直径相等的两个圆是等圆,正确,不符合题意;
B、长度相等的两条弧圆周角不一定相等,它们不一定是等弧,原题的说法是错误的,符合题意;
C、圆中最长的弦是直径,正确,不符合题意;
D、一条直径把圆分成两条弧,这两条弧是等弧,正确,不符合题意,
故选B.
点评:
本题考查了圆的认识,了解圆中有关的定义及性质是解答本题的关键.
3.如图,AB是⊙O的直径,点C、D在
( http: / / www.21cnjy.com )⊙O上,且点C、D在AB的异侧,连结AD、OD、OC.若∠AOC=70°,且AD∥OC,则∠AOD的度数为( )
( http: / / www.21cnjy.com )
A.
70°
B.60°
C.50°
D.
40°
考点:
圆的认识;平行线的性质.
分析:
首先由AD∥OC可以得到∠BOC=∠DAO,又由OD=OA得到∠ADO=∠DAO,由此即可求出∠AOD的度数.
解答:
解:∵AD∥OC,
∴∠AOC=∠DAO=70°,
又∵OD=OA,
∴∠ADO=∠DAO=70°,
∴∠AOD=180﹣70°﹣70°=40°.
故选D.
点评:
此题比较简单,主要考查了平行线的性质、等腰三角形的性质,综合利用它们即可解决问题.
4.如图,弧AD是以等边三角形ABC一边AB为半径的四分之一圆周,P为弧AD上任意一点,若AC=5,则四边形ACBP周长的最大值是( )
( http: / / www.21cnjy.com )
A.
15
B.15+5
C.20
D.
15+5
考点:
圆的认识;等边三角形的性质;等腰直角三角形.
专题:
计算题.
分析:
连结ADBP,PA,由于弧AD是以等边三角形ABC一边AB为半径的四分之一圆周,可得到△ABD为等腰直角三角形,则AD=BD,由于△ABC为等边三角形,所以AC=BC=AB=5,BD=BP=5,当点P与点D重合时,AP最大,四边形ACBP周长的最大值,最大值为AC+BC+BD+AD=15+5.
解答:
解:连结AD,BP,PA,
∵弧AD是以等边三角形ABC一边AB为半径的四分之一圆周,
∴∠ABD=90°,
∴AD=AB,
∵△ABC为等边三角形,
∴AC=BC=AB=5,
∴BD=BP=5,
当点P与点D重合时,四边形ACBP周长的最大值,最大值为AC+BC+BD+AD=5+5+5+5=15+5.
故选B.
( http: / / www.21cnjy.com )
点评:
本题考查了圆的认识:掌握与
( http: / / www.21cnjy.com )圆有关的概念(弦、直径、半径、弧、半圆、优弧、劣弧、等圆、等弧等).也考查了等边三角形的性质和等腰直角三角形的性质.
5.如图,在半圆的直径上作4个正三角形,如这半圆周长为C1,这4个正三角形的周长和为C2,则C1和C2的大小关系是( )
A.
C1>C2
B.C1<C2
C.C1=C2
D.
不能确定
考点:
圆的认识;等边三角形的性质.
分析:
首先设出圆的直径,然后表示出半圆的弧长和三个正三角形的周长和,比较后即可得到答案.
解答:
解:设半圆的直径为a,则半圆周长C1为:aπ,
4个正三角形的周长和C2为:3a,
∵aπ<3a,
∴C1<C2
故选B.
点评:
本题考查了圆的认识及等边三角形的性质,解题的关键是设出圆的直径并表示出C1和C2.
6.在△ABC中,∠C为锐角,分别以AB,AC为直径作半圆,过点B,A,C作,如图所示.若AB=4,AC=2,S1﹣S2=,则S3﹣S4的值是( )
( http: / / www.21cnjy.com )
A.
B.
C.
D.
考点:
圆的认识.
专题:
压轴题.
分析:
首先根据AB、AC的长求得S1+S3和S2+S4的值,然后两值相减即可求得结论.
解答:
解:∵AB=4,AC=2,
∴S1+S3=2π,S2+S4=,
∵S1﹣S2=,
∴(S1+S3)﹣(S2+S4)=(S1﹣S2)+(S3﹣S4)=π
∴S3﹣S4=π,
故选:D.
点评:
本题考查了圆的认识,解题的关键是正确的表示出S1+S3和S2+S4的值.
7.车轮要做成圆形,实际上就是根据圆的特征( )
A.
同弧所对的圆周角相等
B.
直径是圆中最大的弦
C.
圆上各点到圆心的距离相等
D.
圆是中心对称图形
考点:
圆的认识.
分析:
根据车轮的特点和功能进行解答.
解答:
解:车轮做成圆形是为了在行进过程中保持和地面的高度不变,
是利用了圆上各点到圆心的距离相等,
故选C.
点评:
本题考查了对圆的基本认识,即墨经所说:圆,一中同长也.
8.如图,以坐标原点O为圆心的圆与y轴交于点A、B,且OA=1,则点B的坐标是( )
( http: / / www.21cnjy.com )
A.
(0,1)
B.(0,﹣1)
C.(
1,0)
D.
(﹣1,0)
考点:
圆的认识;坐标与图形性质.
分析:
先根据同圆的半径相等得出OB=OA=1,再由点B在y轴的负半轴上即可求出点B的坐标.
解答:
解:∵以坐标原点O为圆心的圆与y轴交于点A、B,且OA=1,
∴点B的坐标是(0,﹣1).
故选B.
点评:
本题考查了对圆的认识及y轴上点的坐标特征,比较简单.
二.填空题(共6小题)
9.如图,以△ABC的边BC为直径的⊙O分别交AB、AC于点D、E,连结OD、OE,若∠A=65°,则∠DOE= 50° .
( http: / / www.21cnjy.com )
考点:
圆的认识;三角形内角和定理;等腰三角形的性质;圆周角定理.
专题:
几何图形问题.
分析:
如图,连接BE.由圆周角定理和三角形内角和定理求得∠ABE=25°,再由“同弧所对的圆周角是所对的圆心角的一半”进行答题.
解答:
解:如图,连接BE.
∵BC为⊙O的直径,
∴∠CEB=∠AEB=90°,
∵∠A=65°,
∴∠ABE=25°,
∴∠DOE=2∠ABE=50°,(圆周角定理)
故答案为:50°.
( http: / / www.21cnjy.com )
点评:
本题考查了圆的认识及三角形的内角和定理等知识,难度不大.
10.如图,以AB为直径的半圆O上有两点D、E,ED与BA的延长线交于点C,且有DC=OE,若∠C=20°,则∠EOB的度数是 60° .
( http: / / www.21cnjy.com )
考点:
圆的认识;等腰三角形的性质.
分析:
利用等边对等角即可证得∠C=∠DOC=20°,然后根据三角形的外角等于不相邻的两个内角的和即可求解.
解答:
解:∵CD=OD=OE,
∴∠C=∠DOC=20°,
∴∠EDO=∠E=40°,
∴∠EOB=∠C+∠E=20°+40°=60°.
故答案为:60°.
点评:
本题主要考查了三角形的外角的性质和等腰三角形的性质,正确理解圆的半径都相等是解题的关键.
11.如图,AB为⊙O直径,点C、D在⊙O上,已知∠AOD=50°,AD∥OC,则∠BOC= 65 度.
( http: / / www.21cnjy.com )
考点:
圆的认识;平行线的性质.
专题:
计算题.
分析:
根据半径相等和等腰三角形的性质得到∠D=∠A,利用三角形内角和定理可计算出∠A,然后根据平行线的性质即可得到∠BOC的度数.
解答:
解:∵OD=OC,
∴∠D=∠A,
而∠AOD=50°,
∴∠A=(180°﹣50°)=65°,
又∵AD∥OC,
∴∠BOC=∠A=65°.
故答案为:65.
( http: / / www.21cnjy.com )
点评:
本题考查了有关圆的知识:圆的半径都相等.也考查了等腰三角形的性质和平行线的性质.
12.如图,AB是⊙O的直径,点C、D在⊙O上,∠BOC=110°,AD∥OC,则∠AOD= 40° .
( http: / / www.21cnjy.com )
考点:
圆的认识;平行线的性质;三角形内角和定理.
专题:
计算题.
分析:
根据三角形内角和定理可求得∠AOC的度数,再根据平行线的性质及三角形内角和定理即可求得∠AOD的度数.
解答:
解:∵∠BOC=110°,∠BOC+∠AOC=180°,
∴∠AOC=70°,
∵AD∥OC,OD=OA,
∴∠D=∠A=70°,
∴∠AOD=180°﹣2∠A=40°.
故答案为:40.
点评:
本题考查平行线性质、圆的认识及三角形内角和定理的运用.
13.如图①是半径为1的圆,在其中挖去2个半径为的圆得到图②,挖去22个半径为()2的圆得到图③…,则第n(n>1)个图形阴影部分的面积是 (1﹣)π .
( http: / / www.21cnjy.com )
考点:
圆的认识.
专题:
规律型.
分析:
先分别求出图②与图③中阴影部分的面积,再从中发现规律,然后根据规律即可得出第n(n>1)个图形阴影部分的面积.
解答:
解:图②中阴影部分的面积为:π×12﹣π×()2×2=π﹣π=(1﹣)π=π;
图③中阴影部分的面积为:π×12﹣π×[()2]2×22=π﹣π=(1﹣)π=π;
图④是半径为1的圆,在其中挖去23个半径为()3的圆得到的,则图④中阴影部分的面积为:π×12﹣π×[()3]2×23=π﹣π=(1﹣)π=π;
…,
则第n(n>1)个图形阴影部分的面积为:π×12﹣π×[()n﹣1]2×2n﹣1=π﹣π=(1﹣)π.
故答案为:(1﹣)π.
点评:
本题考查了对圆的认识及圆的面积公式,从具体的图形中找到规律是解题的关键.
14如图,在⊙O中,半径为5,∠AOB=60°,则弦长AB= 5 .
( http: / / www.21cnjy.com )
考点:
圆的认识;等边三角形的判定与性质.
分析:
由OA=OB,得△OAB为等边三角形进行解答.
解答:
解:∵OA=OB=5,∠AOB=60°,
∴△OAB为等边三角形,
故AB=5.
故答案为:5.
点评:
同圆或等圆的半径相等在解题中是一个重要条件.
三.解答题(共7小题)
15.已知:如图,在⊙O中,AB为弦,C、D两点在AB上,且AC=BD.
求证:△OAC≌△OBD.
( http: / / www.21cnjy.com )
考点:
圆的认识;全等三角形的判定.
专题:
证明题;压轴题.
分析:
根据等边对等角可以证得∠A=∠B,然后根据SAS即可证得两个三角形全等.
解答:
证明:∵OA=OB,
∴∠A=∠B,
∵在△OAC和△OBD中:
,
∴△OAC≌△OBD(SAS).
点评:
本题考查了三角形全等的判定与性质,正确理解三角形的判定定理是关键.
16.如图,CD是⊙O的直径,E是⊙O上一点,∠EOD=48°,A为DC延长线上一点,且AB=OC,求∠A的度数.
( http: / / www.21cnjy.com )
考点:
圆的认识;等腰三角形的性质.
分析:
根据圆的半径,可得等腰三角
( http: / / www.21cnjy.com )形,根据等腰三角形的性质,可得∠A与∠AOB,∠B与∠E的关系,根据三角形的外角的性质,可得关于∠A的方程,根据解方程,可得答案.
解答:
解:如图,连接OB,
由AB=OC,得AB=OC,∠AOB=∠A.
由三角的外角等于与它不相邻的两个内角的和,得
∠EBO=∠A+∠AOB=2∠A.
由OB=OE,得∠E=∠EBO=2∠A.
由∠A+∠E=∠EOD,即∠A+2∠A=48°.
解得∠A=16°.
( http: / / www.21cnjy.com )
点评:
本题考查了圆的认识,利用了圆的性质,等腰三角形的性质,三角形外角的性质.
17.如图所示,AB为⊙O的直径,CD是⊙O的弦,AB、CD的延长线交于点E,已知AB=2DE,∠AEC=20°.求∠AOC的度数.
( http: / / www.21cnjy.com )
考点:
圆的认识;等腰三角形的性质.
专题:
计算题.
分析:
连接OD,如图,由AB=2DE,AB=2OD得到OD=DE,根据等腰三角形的性质得∠DOE=∠E=20°,再利用三角形外角性质得到∠CDO=40°,加上∠C=∠ODC=40°,然后再利用三角形外角性质即可计算出∠AOC.
解答:
解:连接OD,如图,
∵AB=2DE,
而AB=2OD,
∴OD=DE,
∴∠DOE=∠E=20°,
∴∠CDO=∠DOE+∠E=40°,
而OC=OD,
∴∠C=∠ODC=40°,
∴∠AOC=∠C+∠E=60°.
( http: / / www.21cnjy.com )
点评:
本题考查了圆的认识:掌握与圆有关的概念(弦、直径、半径、弧、半圆、优弧、劣弧、等圆、等弧等).也考查了等腰三角形的性质.
18.如图,点O是同心圆的圆心,大圆半径OA,OB分别交小圆于点C,D,求证:AB∥CD.
( http: / / www.21cnjy.com )
考点:
圆的认识;平行线的判定.
专题:
证明题.
分析:
利用半径相等得到OC=OD,则利用等腰三角形的性质得∠OCD=∠ODC,再根据三角形内角和定理得到∠OCD=(180°﹣∠O),同理可得∠OAB=(180°﹣∠O),
则∠OCD=∠OAB,然后根据平行线的判定即可得到结论.
解答:
证明:∵OC=OD,
∴∠OCD=∠ODC,
∴∠OCD=(180°﹣∠O),
∵OA=OB,
∴∠OAB=∠OBA,
∴∠OAB=(180°﹣∠O),
∴∠OCD=∠OAB,
∴AB∥CD.
点评:
本题考查了圆的认识:掌握与圆有关的概念(弦、直径、半径、弧、半圆、优弧、劣弧、等圆、等弧等).
19.已知AB为⊙O的弦,C、D在AB上,且AC=CD=DB,求证:∠AOC=∠DOB.
( http: / / www.21cnjy.com )
考点:
圆的认识;全等三角形的判定与性质.
专题:
证明题.
分析:
先根据等腰三角形的性质由OA=OB得到∠A=∠B,再利用“SAS”证明△OAC≌△OBD,然后根据全等三角形的性质得到结论.
解答:
证明:∵OA=OB,
∴∠A=∠B,
在△OAC和△OBD中,
,
∴△OAC≌△OBD(SAS),
∴∠AOC=∠DOB.
点评:
本题考查了圆的认识:掌握与圆有关的概念(弦、直径、半径、弧、半圆、优弧、劣弧、等圆、等弧等).也考查了全等三角形的判定与性质.
20.如图,AB是半圆O的直径,D是半圆上的一点,∠DOB=75°,DC交BA延长线于E,交半圆于C,且CE=AO,求∠E的度数.
( http: / / www.21cnjy.com )
考点:
圆的认识;等腰三角形的性质.
专题:
计算题.
分析:
如图,由CE=AO,OA=OC得到O
( http: / / www.21cnjy.com )C=EC,则根据等腰三角形的性质得∠E=∠1,再利用三角形外角性质得∠2=∠E+∠1=2∠E,加上∠D=∠2=2∠E,所以∠BOD=∠E+∠D,即∠E+2∠E=75°,然后解方程即可.
解答:
解:如图,
∵CE=AO,
而OA=OC,
∴OC=EC,
∴∠E=∠1,
∴∠2=∠E+∠1=2∠E,
∵OC=OD,
∴∠D=∠2=2∠E,
∵∠BOD=∠E+∠D,
∴∠E+2∠E=75°,
∴∠E=25°.
( http: / / www.21cnjy.com )
点评:
本题考查了圆的认识:掌握与圆有关的概念(弦、直径、半径、弧、半圆、优弧、劣弧、等圆、等弧等).也考查了等腰三角形的性质.
21.如图,点B是线段AC上的一点,分别以AB、BC、CA为直径作半圆,求证:半圆AB的长与半圆BC的长之和等于半圆AC的长.
( http: / / www.21cnjy.com )
考点:
圆的认识.
专题:
证明题.
分析:
根据圆的周长公式可计算出半圆AB的长=πAB,半圆BC的长=πBC,半圆AC的长=πAC,则半圆AB的长+半圆BC的长=π (AB+BC)=π AC,即半圆AB的长与半圆BC的长之和等于半圆AC的长.
解答:
证明:∵半圆AB的长= 2π =πAB,半圆BC的长= 2π =πBC,半圆AC的长= 2π =πAC,
∴半圆AB的长+半圆BC的长=πAB+πBC=π (AB+BC),
∵AB+BC=AC,
∴半圆AB的长+半圆BC的长=π AC,
∴半圆AB的长与半圆BC的长之和等于半圆AC的长.
点评:
本题考查了圆的认识:掌握与圆有关的概念(弦、直径、半径、弧、半圆、优弧、劣弧、等圆、等弧等).
农安县合隆中学
徐亚惠
一.选择题(共8小题)
1.如图,一个小圆沿着一个五边形的边滚动,如果五边形的各边长都和小圆的周长相等,那么当小圆滚动到原来位置时,小圆自身滚动的圈数是( )
( http: / / www.21cnjy.com )
A.4
B.5
C.6
D.10
2.下列说法中,结论错误的是( )
A.直径相等的两个圆是等圆
B.长度相等的两条弧是等弧
C.圆中最长的弦是直径
D.一条弦把圆分成两条弧,这两条弧可能是等弧
3.如图,AB是⊙O的直径,点C、D在⊙
( http: / / www.21cnjy.com )O上,且点C、D在AB的异侧,连结AD、OD、OC.若∠AOC=70°,且AD∥OC,则∠AOD的度数为( )
( http: / / www.21cnjy.com )
A.70°
B.60°
C.50°
D.40°
4.如图,弧AD是以等边三角形ABC一边AB为半径的四分之一圆周,P为弧AD上任意一点,若AC=5,则四边形ACBP周长的最大值是( )
( http: / / www.21cnjy.com )
A.15
B.15+5
C.20
D.15+5
5.如图,在半圆的直径上作4个正三角形,如这半圆周长为C1,这4个正三角形的周长和为C2,则C1和C2的大小关系是( )
A.C1>C2
B.C1<C2
C.C1=C2
D.不能确定
6.在△ABC中,∠C为锐角,分别以AB,AC为直径作半圆,过点B,A,C作,如图所示.若AB=4,AC=2,S1﹣S2=,则S3﹣S4的值是( )
( http: / / www.21cnjy.com )
A.
B.
C.
D.
7.车轮要做成圆形,实际上就是根据圆的特征( )
A.同弧所对的圆周角相等
B.直径是圆中最大的弦
C.圆上各点到圆心的距离相等
D.圆是中心对称图形
8.如图,以坐标原点O为圆心的圆与y轴交于点A、B,且OA=1,则点B的坐标是( )
( http: / / www.21cnjy.com )
A.(0,1)
B.(0,﹣1)
C.(
1,0)
D.(﹣1,0)
二.填空题(共6小题)
9.如图,以△ABC的边BC为直径的⊙O分别交AB、AC于点D、E,连结OD、OE,若∠A=65°,则∠DOE= _________ .
( http: / / www.21cnjy.com )
10.如图,以AB为直径的半圆O上有两点D
( http: / / www.21cnjy.com )、E,ED与BA的延长线交于点C,且有DC=OE,若∠C=20°,则∠EOB的度数是 _________ .
( http: / / www.21cnjy.com )
11.如图,AB为⊙O直径,点C、D在⊙O上,已知∠AOD=50°,AD∥OC,则∠BOC= _________ 度.
( http: / / www.21cnjy.com )
12.如图,AB是⊙O的直径,点C、D在⊙O上,∠BOC=110°,AD∥OC,则∠AOD= _________ .
( http: / / www.21cnjy.com )
13.如图①是半径为1的圆,在其中挖去2个半径为的圆得到图②,挖去22个半径为()2的圆得到图③…,则第n(n>1)个图形阴影部分的面积是 _________ .
( http: / / www.21cnjy.com )
14.如图,在⊙O中,半径为5,∠AOB=60°,则弦长AB= _________ .
( http: / / www.21cnjy.com )
三.解答题(共7小题)
15.已知:如图,在⊙O中,AB为弦,C、D两点在AB上,且AC=BD.
求证:△OAC≌△OBD.
( http: / / www.21cnjy.com )
16.如图,CD是⊙O的直径,E是⊙O上一点,∠EOD=48°,A为DC延长线上一点,且AB=OC,求∠A的度数.
( http: / / www.21cnjy.com )
17.如图所示,AB为⊙O的直径,CD是⊙O的弦,AB、CD的延长线交于点E,已知AB=2DE,∠AEC=20°.求∠AOC的度数.
( http: / / www.21cnjy.com )
18.如图,点O是同心圆的圆心,大圆半径OA,OB分别交小圆于点C,D,求证:AB∥CD.
( http: / / www.21cnjy.com )
19.已知AB为⊙O的弦,C、D在AB上,且AC=CD=DB,求证:∠AOC=∠DOB.
( http: / / www.21cnjy.com )
20.如图,AB是半圆O的直径,D是半圆上的一点,∠DOB=75°,DC交BA延长线于E,交半圆于C,且CE=AO,求∠E的度数.
( http: / / www.21cnjy.com )
21.如图,点B是线段AC上的一点,分别以AB、BC、CA为直径作半圆,求证:半圆AB的长与半圆BC的长之和等于半圆AC的长.
( http: / / www.21cnjy.com )
27.1.1圆的基本元素
参考答案与试题解析
一.选择题(共8小题)
1.如图,一个小圆沿着一个五边形的边滚动,如果五边形的各边长都和小圆的周长相等,那么当小圆滚动到原来位置时,小圆自身滚动的圈数是( )
( http: / / www.21cnjy.com )
A.
4
B.5
C.6
D.
10
考点:
圆的认识;多边形内角与外角.
专题:
压轴题.
分析:
因为五边形的各边长都和小圆的周长相
( http: / / www.21cnjy.com )等,所有小圆在每一边上滚动正好一周,另外五边形的外角和为360°,所有小圆在五个角处共滚动一周,可以求出小圆滚动的圈数.
解答:
解:因为五边形的各
( http: / / www.21cnjy.com )边长都和小圆的周长相等,所有小圆在每一边上滚动正好一周,在五条边上共滚动了5周.由于每次小圆从五边形的一边滚动到另一边时,都会翻转72°,所以小圆在五个角处共滚动一周.因此,总共是滚动了6周.
故选:C.
点评:
本题考查的是对圆的认识,根据圆的周长与五边形的边长相等,可以知道圆在每边上滚动一周.然后由多边形外角和是360°,可以知道圆在五个角处滚动一周.因此可以求出滚动的总圈数.
2.下列说法中,结论错误的是( )
A.
直径相等的两个圆是等圆
B.
长度相等的两条弧是等弧
C.
圆中最长的弦是直径
D.
一条弦把圆分成两条弧,这两条弧可能是等弧
考点:
圆的认识.
分析:
利用圆的有关定义进行判断后利用排除法即可得到正确的答案;
解答:
解:A、直径相等的两个圆是等圆,正确,不符合题意;
B、长度相等的两条弧圆周角不一定相等,它们不一定是等弧,原题的说法是错误的,符合题意;
C、圆中最长的弦是直径,正确,不符合题意;
D、一条直径把圆分成两条弧,这两条弧是等弧,正确,不符合题意,
故选B.
点评:
本题考查了圆的认识,了解圆中有关的定义及性质是解答本题的关键.
3.如图,AB是⊙O的直径,点C、D在
( http: / / www.21cnjy.com )⊙O上,且点C、D在AB的异侧,连结AD、OD、OC.若∠AOC=70°,且AD∥OC,则∠AOD的度数为( )
( http: / / www.21cnjy.com )
A.
70°
B.60°
C.50°
D.
40°
考点:
圆的认识;平行线的性质.
分析:
首先由AD∥OC可以得到∠BOC=∠DAO,又由OD=OA得到∠ADO=∠DAO,由此即可求出∠AOD的度数.
解答:
解:∵AD∥OC,
∴∠AOC=∠DAO=70°,
又∵OD=OA,
∴∠ADO=∠DAO=70°,
∴∠AOD=180﹣70°﹣70°=40°.
故选D.
点评:
此题比较简单,主要考查了平行线的性质、等腰三角形的性质,综合利用它们即可解决问题.
4.如图,弧AD是以等边三角形ABC一边AB为半径的四分之一圆周,P为弧AD上任意一点,若AC=5,则四边形ACBP周长的最大值是( )
( http: / / www.21cnjy.com )
A.
15
B.15+5
C.20
D.
15+5
考点:
圆的认识;等边三角形的性质;等腰直角三角形.
专题:
计算题.
分析:
连结ADBP,PA,由于弧AD是以等边三角形ABC一边AB为半径的四分之一圆周,可得到△ABD为等腰直角三角形,则AD=BD,由于△ABC为等边三角形,所以AC=BC=AB=5,BD=BP=5,当点P与点D重合时,AP最大,四边形ACBP周长的最大值,最大值为AC+BC+BD+AD=15+5.
解答:
解:连结AD,BP,PA,
∵弧AD是以等边三角形ABC一边AB为半径的四分之一圆周,
∴∠ABD=90°,
∴AD=AB,
∵△ABC为等边三角形,
∴AC=BC=AB=5,
∴BD=BP=5,
当点P与点D重合时,四边形ACBP周长的最大值,最大值为AC+BC+BD+AD=5+5+5+5=15+5.
故选B.
( http: / / www.21cnjy.com )
点评:
本题考查了圆的认识:掌握与
( http: / / www.21cnjy.com )圆有关的概念(弦、直径、半径、弧、半圆、优弧、劣弧、等圆、等弧等).也考查了等边三角形的性质和等腰直角三角形的性质.
5.如图,在半圆的直径上作4个正三角形,如这半圆周长为C1,这4个正三角形的周长和为C2,则C1和C2的大小关系是( )
A.
C1>C2
B.C1<C2
C.C1=C2
D.
不能确定
考点:
圆的认识;等边三角形的性质.
分析:
首先设出圆的直径,然后表示出半圆的弧长和三个正三角形的周长和,比较后即可得到答案.
解答:
解:设半圆的直径为a,则半圆周长C1为:aπ,
4个正三角形的周长和C2为:3a,
∵aπ<3a,
∴C1<C2
故选B.
点评:
本题考查了圆的认识及等边三角形的性质,解题的关键是设出圆的直径并表示出C1和C2.
6.在△ABC中,∠C为锐角,分别以AB,AC为直径作半圆,过点B,A,C作,如图所示.若AB=4,AC=2,S1﹣S2=,则S3﹣S4的值是( )
( http: / / www.21cnjy.com )
A.
B.
C.
D.
考点:
圆的认识.
专题:
压轴题.
分析:
首先根据AB、AC的长求得S1+S3和S2+S4的值,然后两值相减即可求得结论.
解答:
解:∵AB=4,AC=2,
∴S1+S3=2π,S2+S4=,
∵S1﹣S2=,
∴(S1+S3)﹣(S2+S4)=(S1﹣S2)+(S3﹣S4)=π
∴S3﹣S4=π,
故选:D.
点评:
本题考查了圆的认识,解题的关键是正确的表示出S1+S3和S2+S4的值.
7.车轮要做成圆形,实际上就是根据圆的特征( )
A.
同弧所对的圆周角相等
B.
直径是圆中最大的弦
C.
圆上各点到圆心的距离相等
D.
圆是中心对称图形
考点:
圆的认识.
分析:
根据车轮的特点和功能进行解答.
解答:
解:车轮做成圆形是为了在行进过程中保持和地面的高度不变,
是利用了圆上各点到圆心的距离相等,
故选C.
点评:
本题考查了对圆的基本认识,即墨经所说:圆,一中同长也.
8.如图,以坐标原点O为圆心的圆与y轴交于点A、B,且OA=1,则点B的坐标是( )
( http: / / www.21cnjy.com )
A.
(0,1)
B.(0,﹣1)
C.(
1,0)
D.
(﹣1,0)
考点:
圆的认识;坐标与图形性质.
分析:
先根据同圆的半径相等得出OB=OA=1,再由点B在y轴的负半轴上即可求出点B的坐标.
解答:
解:∵以坐标原点O为圆心的圆与y轴交于点A、B,且OA=1,
∴点B的坐标是(0,﹣1).
故选B.
点评:
本题考查了对圆的认识及y轴上点的坐标特征,比较简单.
二.填空题(共6小题)
9.如图,以△ABC的边BC为直径的⊙O分别交AB、AC于点D、E,连结OD、OE,若∠A=65°,则∠DOE= 50° .
( http: / / www.21cnjy.com )
考点:
圆的认识;三角形内角和定理;等腰三角形的性质;圆周角定理.
专题:
几何图形问题.
分析:
如图,连接BE.由圆周角定理和三角形内角和定理求得∠ABE=25°,再由“同弧所对的圆周角是所对的圆心角的一半”进行答题.
解答:
解:如图,连接BE.
∵BC为⊙O的直径,
∴∠CEB=∠AEB=90°,
∵∠A=65°,
∴∠ABE=25°,
∴∠DOE=2∠ABE=50°,(圆周角定理)
故答案为:50°.
( http: / / www.21cnjy.com )
点评:
本题考查了圆的认识及三角形的内角和定理等知识,难度不大.
10.如图,以AB为直径的半圆O上有两点D、E,ED与BA的延长线交于点C,且有DC=OE,若∠C=20°,则∠EOB的度数是 60° .
( http: / / www.21cnjy.com )
考点:
圆的认识;等腰三角形的性质.
分析:
利用等边对等角即可证得∠C=∠DOC=20°,然后根据三角形的外角等于不相邻的两个内角的和即可求解.
解答:
解:∵CD=OD=OE,
∴∠C=∠DOC=20°,
∴∠EDO=∠E=40°,
∴∠EOB=∠C+∠E=20°+40°=60°.
故答案为:60°.
点评:
本题主要考查了三角形的外角的性质和等腰三角形的性质,正确理解圆的半径都相等是解题的关键.
11.如图,AB为⊙O直径,点C、D在⊙O上,已知∠AOD=50°,AD∥OC,则∠BOC= 65 度.
( http: / / www.21cnjy.com )
考点:
圆的认识;平行线的性质.
专题:
计算题.
分析:
根据半径相等和等腰三角形的性质得到∠D=∠A,利用三角形内角和定理可计算出∠A,然后根据平行线的性质即可得到∠BOC的度数.
解答:
解:∵OD=OC,
∴∠D=∠A,
而∠AOD=50°,
∴∠A=(180°﹣50°)=65°,
又∵AD∥OC,
∴∠BOC=∠A=65°.
故答案为:65.
( http: / / www.21cnjy.com )
点评:
本题考查了有关圆的知识:圆的半径都相等.也考查了等腰三角形的性质和平行线的性质.
12.如图,AB是⊙O的直径,点C、D在⊙O上,∠BOC=110°,AD∥OC,则∠AOD= 40° .
( http: / / www.21cnjy.com )
考点:
圆的认识;平行线的性质;三角形内角和定理.
专题:
计算题.
分析:
根据三角形内角和定理可求得∠AOC的度数,再根据平行线的性质及三角形内角和定理即可求得∠AOD的度数.
解答:
解:∵∠BOC=110°,∠BOC+∠AOC=180°,
∴∠AOC=70°,
∵AD∥OC,OD=OA,
∴∠D=∠A=70°,
∴∠AOD=180°﹣2∠A=40°.
故答案为:40.
点评:
本题考查平行线性质、圆的认识及三角形内角和定理的运用.
13.如图①是半径为1的圆,在其中挖去2个半径为的圆得到图②,挖去22个半径为()2的圆得到图③…,则第n(n>1)个图形阴影部分的面积是 (1﹣)π .
( http: / / www.21cnjy.com )
考点:
圆的认识.
专题:
规律型.
分析:
先分别求出图②与图③中阴影部分的面积,再从中发现规律,然后根据规律即可得出第n(n>1)个图形阴影部分的面积.
解答:
解:图②中阴影部分的面积为:π×12﹣π×()2×2=π﹣π=(1﹣)π=π;
图③中阴影部分的面积为:π×12﹣π×[()2]2×22=π﹣π=(1﹣)π=π;
图④是半径为1的圆,在其中挖去23个半径为()3的圆得到的,则图④中阴影部分的面积为:π×12﹣π×[()3]2×23=π﹣π=(1﹣)π=π;
…,
则第n(n>1)个图形阴影部分的面积为:π×12﹣π×[()n﹣1]2×2n﹣1=π﹣π=(1﹣)π.
故答案为:(1﹣)π.
点评:
本题考查了对圆的认识及圆的面积公式,从具体的图形中找到规律是解题的关键.
14如图,在⊙O中,半径为5,∠AOB=60°,则弦长AB= 5 .
( http: / / www.21cnjy.com )
考点:
圆的认识;等边三角形的判定与性质.
分析:
由OA=OB,得△OAB为等边三角形进行解答.
解答:
解:∵OA=OB=5,∠AOB=60°,
∴△OAB为等边三角形,
故AB=5.
故答案为:5.
点评:
同圆或等圆的半径相等在解题中是一个重要条件.
三.解答题(共7小题)
15.已知:如图,在⊙O中,AB为弦,C、D两点在AB上,且AC=BD.
求证:△OAC≌△OBD.
( http: / / www.21cnjy.com )
考点:
圆的认识;全等三角形的判定.
专题:
证明题;压轴题.
分析:
根据等边对等角可以证得∠A=∠B,然后根据SAS即可证得两个三角形全等.
解答:
证明:∵OA=OB,
∴∠A=∠B,
∵在△OAC和△OBD中:
,
∴△OAC≌△OBD(SAS).
点评:
本题考查了三角形全等的判定与性质,正确理解三角形的判定定理是关键.
16.如图,CD是⊙O的直径,E是⊙O上一点,∠EOD=48°,A为DC延长线上一点,且AB=OC,求∠A的度数.
( http: / / www.21cnjy.com )
考点:
圆的认识;等腰三角形的性质.
分析:
根据圆的半径,可得等腰三角
( http: / / www.21cnjy.com )形,根据等腰三角形的性质,可得∠A与∠AOB,∠B与∠E的关系,根据三角形的外角的性质,可得关于∠A的方程,根据解方程,可得答案.
解答:
解:如图,连接OB,
由AB=OC,得AB=OC,∠AOB=∠A.
由三角的外角等于与它不相邻的两个内角的和,得
∠EBO=∠A+∠AOB=2∠A.
由OB=OE,得∠E=∠EBO=2∠A.
由∠A+∠E=∠EOD,即∠A+2∠A=48°.
解得∠A=16°.
( http: / / www.21cnjy.com )
点评:
本题考查了圆的认识,利用了圆的性质,等腰三角形的性质,三角形外角的性质.
17.如图所示,AB为⊙O的直径,CD是⊙O的弦,AB、CD的延长线交于点E,已知AB=2DE,∠AEC=20°.求∠AOC的度数.
( http: / / www.21cnjy.com )
考点:
圆的认识;等腰三角形的性质.
专题:
计算题.
分析:
连接OD,如图,由AB=2DE,AB=2OD得到OD=DE,根据等腰三角形的性质得∠DOE=∠E=20°,再利用三角形外角性质得到∠CDO=40°,加上∠C=∠ODC=40°,然后再利用三角形外角性质即可计算出∠AOC.
解答:
解:连接OD,如图,
∵AB=2DE,
而AB=2OD,
∴OD=DE,
∴∠DOE=∠E=20°,
∴∠CDO=∠DOE+∠E=40°,
而OC=OD,
∴∠C=∠ODC=40°,
∴∠AOC=∠C+∠E=60°.
( http: / / www.21cnjy.com )
点评:
本题考查了圆的认识:掌握与圆有关的概念(弦、直径、半径、弧、半圆、优弧、劣弧、等圆、等弧等).也考查了等腰三角形的性质.
18.如图,点O是同心圆的圆心,大圆半径OA,OB分别交小圆于点C,D,求证:AB∥CD.
( http: / / www.21cnjy.com )
考点:
圆的认识;平行线的判定.
专题:
证明题.
分析:
利用半径相等得到OC=OD,则利用等腰三角形的性质得∠OCD=∠ODC,再根据三角形内角和定理得到∠OCD=(180°﹣∠O),同理可得∠OAB=(180°﹣∠O),
则∠OCD=∠OAB,然后根据平行线的判定即可得到结论.
解答:
证明:∵OC=OD,
∴∠OCD=∠ODC,
∴∠OCD=(180°﹣∠O),
∵OA=OB,
∴∠OAB=∠OBA,
∴∠OAB=(180°﹣∠O),
∴∠OCD=∠OAB,
∴AB∥CD.
点评:
本题考查了圆的认识:掌握与圆有关的概念(弦、直径、半径、弧、半圆、优弧、劣弧、等圆、等弧等).
19.已知AB为⊙O的弦,C、D在AB上,且AC=CD=DB,求证:∠AOC=∠DOB.
( http: / / www.21cnjy.com )
考点:
圆的认识;全等三角形的判定与性质.
专题:
证明题.
分析:
先根据等腰三角形的性质由OA=OB得到∠A=∠B,再利用“SAS”证明△OAC≌△OBD,然后根据全等三角形的性质得到结论.
解答:
证明:∵OA=OB,
∴∠A=∠B,
在△OAC和△OBD中,
,
∴△OAC≌△OBD(SAS),
∴∠AOC=∠DOB.
点评:
本题考查了圆的认识:掌握与圆有关的概念(弦、直径、半径、弧、半圆、优弧、劣弧、等圆、等弧等).也考查了全等三角形的判定与性质.
20.如图,AB是半圆O的直径,D是半圆上的一点,∠DOB=75°,DC交BA延长线于E,交半圆于C,且CE=AO,求∠E的度数.
( http: / / www.21cnjy.com )
考点:
圆的认识;等腰三角形的性质.
专题:
计算题.
分析:
如图,由CE=AO,OA=OC得到O
( http: / / www.21cnjy.com )C=EC,则根据等腰三角形的性质得∠E=∠1,再利用三角形外角性质得∠2=∠E+∠1=2∠E,加上∠D=∠2=2∠E,所以∠BOD=∠E+∠D,即∠E+2∠E=75°,然后解方程即可.
解答:
解:如图,
∵CE=AO,
而OA=OC,
∴OC=EC,
∴∠E=∠1,
∴∠2=∠E+∠1=2∠E,
∵OC=OD,
∴∠D=∠2=2∠E,
∵∠BOD=∠E+∠D,
∴∠E+2∠E=75°,
∴∠E=25°.
( http: / / www.21cnjy.com )
点评:
本题考查了圆的认识:掌握与圆有关的概念(弦、直径、半径、弧、半圆、优弧、劣弧、等圆、等弧等).也考查了等腰三角形的性质.
21.如图,点B是线段AC上的一点,分别以AB、BC、CA为直径作半圆,求证:半圆AB的长与半圆BC的长之和等于半圆AC的长.
( http: / / www.21cnjy.com )
考点:
圆的认识.
专题:
证明题.
分析:
根据圆的周长公式可计算出半圆AB的长=πAB,半圆BC的长=πBC,半圆AC的长=πAC,则半圆AB的长+半圆BC的长=π (AB+BC)=π AC,即半圆AB的长与半圆BC的长之和等于半圆AC的长.
解答:
证明:∵半圆AB的长= 2π =πAB,半圆BC的长= 2π =πBC,半圆AC的长= 2π =πAC,
∴半圆AB的长+半圆BC的长=πAB+πBC=π (AB+BC),
∵AB+BC=AC,
∴半圆AB的长+半圆BC的长=π AC,
∴半圆AB的长与半圆BC的长之和等于半圆AC的长.
点评:
本题考查了圆的认识:掌握与圆有关的概念(弦、直径、半径、弧、半圆、优弧、劣弧、等圆、等弧等).
