华师大版九年级数学下27.1.2圆的对称性(2)同步练习(解析版)
文档属性
| 名称 | 华师大版九年级数学下27.1.2圆的对称性(2)同步练习(解析版) |
|
|
| 格式 | zip | ||
| 文件大小 | 467.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-11-07 00:00:00 | ||
图片预览




文档简介
27.1.2圆的对称性2
一.选择题(共8小题)
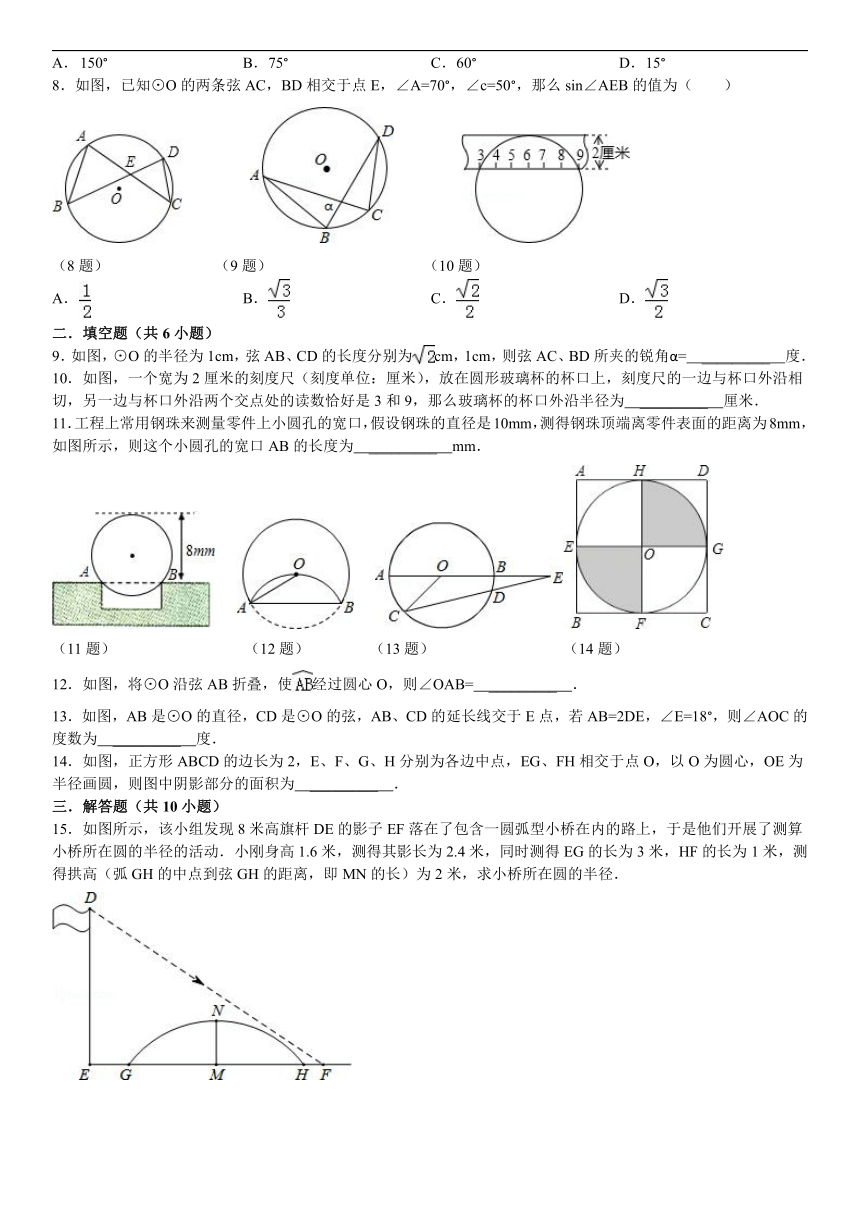
1.如图,直线l1∥l2,点A在直线l1上,以点A为圆心,适当长为半径画弧,分别交直线l1、l2于B、C两点,连接AC、BC.若∠ABC=54°,则∠1的大小为( )
(1题)
(2题)
A.
36°
B.
54°
C.
72°
D.
73°
2.
CD是⊙O的一条弦,作直径AB,使AB⊥CD,垂足为E,若AB=10,CD=8,则BE的长是( )
A.
8
B.
2
C.
2或8
D.
3或7
3.如图,圆心在y轴的负半轴上,半径为5的⊙B与y轴的正半轴交于点A(0,1),过点P(0,﹣7)的直线l与⊙B相交于C,D两点.则弦CD长的所有可能的整数值有( )
A.
1个
B.
2个
C.
3个
D.
4个
4.如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB交于点D,则AD的长为( )
(4题)
(5题)
A.
B.
C.
D.
5.小英家的圆形镜子被打碎了,她拿了如图(网格中的每个小正方形边长为1)的一块碎片到玻璃店,配制成形状、大小与原来一致的镜面,则这个镜面的半径是( )
A.
2
B.
C.
2
D.
3
6.在圆柱形油槽内装有一些油.截面如图,油面宽AB为6分米,如果再注入一些油后,油面AB上升1分米,油面宽变为8分米,圆柱形油槽直径MN为( )
(6题)
(7题)
A.
6分米
B.
8分米
C.
10分米
D.
12分米
7.如图所示,在⊙O中,,∠A=30°,则∠B=( )
A.
150°
B.
75°
C.
60°
D.
15°
8.如图,已知⊙O的两条弦AC,BD相交于点E,∠A=70°,∠c=50°,那么sin∠AEB的值为( )
(8题)
(9题)
(10题)
A.
B.
C.
D.
二.填空题(共6小题)
9.如图,⊙O的半径为1cm,弦AB、CD的长度分别为cm,1cm,则弦AC、BD所夹的锐角α= _________ 度.
10.如图,一个宽为2厘米的刻度尺(刻度单位:厘米),放在圆形玻璃杯的杯口上,刻度尺的一边与杯口外沿相切,另一边与杯口外沿两个交点处的读数恰好是3和9,那么玻璃杯的杯口外沿半径为 _________ 厘米.
11.工程上常用钢珠来测量零件上小圆孔的宽口,假设钢珠的直径是10mm,测得钢珠顶端离零件表面的距离为8mm,如图所示,则这个小圆孔的宽口AB的长度为 _________ mm.
(11题)
(12题)
(13题)
(14题)
12.如图,将⊙O沿弦AB折叠,使经过圆心O,则∠OAB= _________ .
13.如图,AB是⊙O的直径,CD是⊙O的弦,AB、CD的延长线交于E点,若AB=2DE,∠E=18°,则∠AOC的度数为 _________ 度.
14.如图,正方形ABCD的边长为2,E、F、G、H分别为各边中点,EG、FH相交于点O,以O为圆心,OE为半径画圆,则图中阴影部分的面积为 _________ .
三.解答题(共10小题)
15.如图所示,该小组发现8米高旗杆DE的影子EF落在了包含一圆弧型小桥在内的路上,于是他们开展了测算小桥所在圆的半径的活动.小刚身高1.6米,测得其影长为2.4米,同时测得EG的长为3米,HF的长为1米,测得拱高(弧GH的中点到弦GH的距离,即MN的长)为2米,求小桥所在圆的半径.
16.如图,在同一平面内,有一组平行线l1、l2、l3,相邻两条平行线之间的距离均为4,点O在直线l1上,⊙O与直线l3的交点为A、B,AB=12,求⊙O的半径.
17.如图,⊙O的半径为17cm,弦AB∥CD,AB=30cm,CD=16cm,圆心O位于AB,CD的上方,求AB和CD的距离.
18.机器人“海宝”在某圆形区域表演“按指令行走”,如图所示,“海宝”从圆心O出发,先沿北偏西67.4°方向行走13米至点A处,再沿正南方向行走14米至点B处,最后沿正东方向行走至点C处,点B、C都在圆O上.
(1)求弦BC的长;(2)求圆O的半径长.(本题参考数据:sin67.4°=,cos67.4°=,tan67.4°=)
19.如图,平面直角坐标系中,以点C(2,)为圆心,以2为半径的圆与x轴交于A,B两点.
(1)求A,B两点的坐标;
(2)若二次函数y=x2+bx+c的图象经过点A,B,试确定此二次函数的解析式.
20.如图,是一个匀速旋转(指每分钟旋转的弧长或圆心角相同)的摩天轮的示意图,O为圆心,AB为水平地面,假设摩天轮的直径为80米,最低点C离地面为6米,旋转一周所用的时间为6分钟,小明从点C乘坐摩天轮(身高忽略不计),请问:
(1)经过2分钟后,小明离开地面的高度大约是多少米?
(2)若小明到了最高点,在视线没有阻挡的情况下能看到周围3公里远的地面景物,则他看到的地面景物有多大面积?(精确到1平方公里)
21.如图,台风中心位于点P,并沿东北方向PQ移动,已知台风移动的速度为40千米/时,受影响区域的半径为260千米,B市位于点P的北偏东75°方向上,距离P点480千米.
(1)说明本次台风是否会影响B市;
(2)若这次台风会影响B市,求B市受台风影响的时间.
22.如图,将一个两边都带有刻度的直尺放在半圆形纸片上,使其一边经过圆心O,另一边所在直线与半圆相交于点D,E,量出半径OC=5cm,弦DE=8cm,求直尺的宽.
23.如图是一个半圆形桥洞截面示意图,圆心为O,直径AB是河底线,弦CD是水位线,CD∥AB,且CD=24
m,OE⊥CD于点E.已测得sin∠DOE=.
(1)求半径OD;
(2)根据需要,水面要以每小时0.5
m的速度下降,则经过多长时间才能将水排干?
27.1.2圆的对称性2
参考答案与试题解析
一.选择题(共8小题)
1.如图,直线l1∥l2,点A在直线l1上,以点A为圆心,适当长为半径画弧,分别交直线l1、l2于B、C两点,连接AC、BC.若∠ABC=54°,则∠1的大小为( )
A.
36°
B.
54°
C.
72°
D.
73°
考点:
平行线的性质;圆的认识.
专题:
压轴题.
分析:
由l1∥l2,∠ABC=54°,根据两直线平行,内错角相等,即可求得∠2的度数,又由以点A为圆心,适当长为半径画弧,分别交直线l1、l2于B、C两点,连接AC、BC,可得AC=AB,即可证得∠ACB=∠ABC=54°,然后由平角的定义即可求得答案.
解答:
解:∵l1∥l2,∠ABC=54°,
∴∠2=∠ABC=54°,
∵以点A为圆心,适当长为半径画弧,分别交直线l1、l2于B、C两点,
∴AC=AB,
∴∠ACB=∠ABC=54°,
∵∠1+∠ACB+∠2=180°,
∴∠1=72°.
故选C.
点评:
此题考查了平行线的性质与等腰三角形的性质,以及平角的定义.注意两直线平行,内错角相等.
2.CD是⊙O的一条弦,作直径AB,使AB⊥CD,垂足为E,若AB=10,CD=8,则BE的长是( )
A.
8
B.
2
C.
2或8
D.
3或7
考点:
垂径定理;勾股定理.
专题:
计算题.
分析:
连结OC,根据垂径定理得到CE=4,再根据勾股定理计算出OE=3,分类讨论:当点E在半径OB上时,BE=OB﹣OE;当点E在半径OA上时,BE=OB+OE,然后把CE、OE的值代入计算即可.
解答:
解:如图,连结OC,
∵直径AB⊥CD,
∴CE=DE=CD=×8=4,
在Rt△OCE中,OC=AB=5,
∴OE==3,
当点E在半径OB上时,BE=OB﹣OE=5﹣3=2,
当点E在半径OA上时,BE=OB+OE=5+3=8,
∴BE的长为2或8.
故选C.
点评:
本题考查了垂径定理:平分弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了勾股定理.
3.如图,圆心在y轴的负半轴上,半径为5的⊙B与y轴的正半轴交于点A(0,1),过点P(0,﹣7)的直线l与⊙B相交于C,D两点.则弦CD长的所有可能的整数值有( )
A.
1个
B.
2个
C.
3个
D.
4个
考点:
垂径定理;坐标与图形性质;勾股定理.
专题:
压轴题.
分析:
求出线段CD的最小值,及线段CD的最大值,从而可判断弦CD长的所有可能的整数值.
解答:
解:∵点A的坐标为(0,1),圆的半径为5,
∴点B的坐标为(0,﹣4),
又∵点P的坐标为(0,﹣7),
∴BP=3,
①当CD垂直圆的直径AE时,CD的值最小,
连接BC,在Rt△BCP中,CP==4;
故CD=2CP=8,
②当CD经过圆心时,CD的值最大,此时CD=直径AE=10;
所以,8≤CD≤10,
综上可得:弦CD长的所有可能的整数值有:8,9,10,共3个.
故选C.
点评:
本题考查了垂径定理的知识,解答本题的关键是熟练掌握垂直弦的直径平分弦,本题需要讨论两个极值点,有一定难度.
4.如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB交于点D,则AD的长为( )
A.
B.
C.
D.
考点:
垂径定理;勾股定理.
专题:
探究型.
分析:
先根据勾股定理求出AB的长,过C作CM⊥AB,交AB于点M,由垂径定理可知M为AD的中点,由三角形的面积可求出CM的长,在Rt△ACM中,根据勾股定理可求出AM的长,进而可得出结论.
解答:
解:∵在Rt△ABC中,∠ACB=90°,AC=3,BC=4,
∴AB===5,
过C作CM⊥AB,交AB于点M,如图所示,
∵CM⊥AB,
∴M为AD的中点,
∵S△ABC=AC BC=AB CM,且AC=3,BC=4,AB=5,
∴CM=,
在Rt△ACM中,根据勾股定理得:AC2=AM2+CM2,即9=AM2+()2,
解得:AM=,
∴AD=2AM=.
故选C.
点评:
本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
5.小英家的圆形镜子被打碎了,她拿了如图(网格中的每个小正方形边长为1)的一块碎片到玻璃店,配制成形状、大小与原来一致的镜面,则这个镜面的半径是( )
A.
2
B.
C.
2
D.
3
考点:
垂径定理的应用;勾股定理.
专题:
网格型.
分析:
在网格中找点A、B、D(如图),作AB,BD的中垂线,交点O就是圆心,故OA即为此圆的半径,根据勾股定理求出OA的长即可.
解答:
解:如图所示,作AB,BD的中垂线,交点O就是圆心.
连接OA、OB,
∵OC⊥AB,OA=OB
∴O即为此圆形镜子的圆心,
∵AC=1,OC=2,
∴OA===.
故选B.
点评:
本题考查的是垂径定理在实际生活中的运用,根据题意构造出直角三角形是解答此题的关键.
6.在圆柱形油槽内装有一些油.截面如图,油面宽AB为6分米,如果再注入一些油后,油面AB上升1分米,油面宽变为8分米,圆柱形油槽直径MN为( )
A.
6分米
B.
8分米
C.
10分米
D.
12分米
考点:
垂径定理的应用.
专题:
压轴题.
分析:
如图,油面AB上升1分米得到油面CD,依题意得AB=6,CD=8,过O点作AB的垂线,垂足为E,交CD于F点,连接OA,OC,由垂径定理,得AE=AB=3,CF=CD=4,设OE=x,则OF=x﹣1,在Rt△OAE中,OA2=AE2+OE2,在Rt△OCF中,OC2=CF2+OF2,由OA=OC,列方程求x即可求半径OA,得出直径MN.
解答:
解:如图,依题意得AB=6,CD=8,过O点作AB的垂线,垂足为E,交CD于F点,连接OA,OC,
由垂径定理,得AE=AB=3,CF=CD=4,
设OE=x,则OF=x﹣1,
在Rt△OAE中,OA2=AE2+OE2,
在Rt△OCF中,OC2=CF2+OF2,
∵OA=OC,
∴32+x2=42+(x﹣1)2,
解得x=4,
∴半径OA==5,
∴直径MN=2OA=10分米.
故选C.
点评:
本题考查了垂径定理的运用.关键是利用垂径定理得出两个直角三角形,根据勾股定理表示半径的平方,根据半径相等列方程求解.
7.如图所示,在⊙O中,,∠A=30°,则∠B=( )
A.
150°
B.
75°
C.
60°
D.
15°
考点:
圆心角、弧、弦的关系.
分析:
先根据等弧所对的弦相等求得AB=AC,从而判定△ABC是等腰三角形;然后根据等腰三角形的两个底角相等得出∠B=∠C;最后由三角形的内角和定理求角B的度数即可.
解答:
解:∵在⊙O中,,
∴AB=AC,
∴△ABC是等腰三角形,
∴∠B=∠C;
又∠A=30°,
∴∠B==75°(三角形内角和定理).
故选B.
点评:
本题综合考查了圆心角、弧、弦的关系,以及等腰三角形的性质.解题的关键是根据等弧对等弦推知△ABC是等腰三角形.
8.如图,已知⊙O的两条弦AC,BD相交于点E,∠A=70°,∠c=50°,那么sin∠AEB的值为( )
A.
B.
C.
D.
考点:
特殊角的三角函数值;三角形内角和定理;圆心角、弧、弦的关系.
分析:
根据三角形的内角和是180°求得∠AEB的度数,再根据特殊角的锐角三角函数值求解.
解答:
解:∵∠A=70°,∠C=50°,
∴∠B=∠C=50°,∠AEB=60°,
∴sin∠AEB=.
故选D.
点评:
考查了圆周角定理、三角形的内角和是180°,还要熟记特殊角的锐角三角函数值.
二.填空题(共6小题)
9.如图,⊙O的半径为1cm,弦AB、CD的长度分别为cm,1cm,则弦AC、BD所夹的锐角α= 75 度.
考点:
圆心角、弧、弦的关系;三角形的外角性质;勾股定理;垂径定理.
专题:
压轴题.
分析:
根据勾股定理的逆定理可证△AOB是等腰直角三角形,故可求∠OAB=∠OBA=45°,又由已知可证△COD是等边三角形,所以∠ODC=∠OCD=60°,根据圆周角的性质可证∠CDB=∠CAB,而∠ODB=∠OBD,所以∠CAB+∠OBD=∠CDB+∠ODB=∠ODC=60°,再根据三角形的内角和定理可求α.
解答:
解:连接OA、OB、OC、OD,
∵OA=OB=OC=OD=1,AB=,CD=1,
∴OA2+OB2=AB2,
∴△AOB是等腰直角三角形,
△COD是等边三角形,
∴∠OAB=∠OBA=45°,∠ODC=∠OCD=60°,
∵∠CDB=∠CAB,∠ODB=∠OBD,
∴α=180°﹣∠CAB﹣∠OBA﹣∠OBD=180°﹣∠OBA﹣(∠CDB+∠ODB)=180°﹣45°﹣60°=75°.
点评:
本题考查了勾股定理的逆定理,圆周角的性质,等边三角形的性质以及三角形的内角和定理.
10.如图,一个宽为2厘米的刻度尺(刻度单位:厘米),放在圆形玻璃杯的杯口上,刻度尺的一边与杯口外沿相切,另一边与杯口外沿两个交点处的读数恰好是3和9,那么玻璃杯的杯口外沿半径为 厘米.
考点:
垂径定理的应用;勾股定理.
专题:
压轴题.
分析:
先求出弦AC的长,再过点O作OB⊥AC于点B,由垂径定理可得出AB的长,设杯口的半径为r,则OB=r﹣2,OA=r,在Rt△AOB中根据勾股定理求出r的值即可.
解答:
解:∵杯口外沿两个交点处的读数恰好是3和9,
∴AC=9﹣3=6,
过点O作OB⊥AC于点B,则AB=AC=×6=3cm,
设杯口的半径为r,则OB=r﹣2,OA=r,
在Rt△AOB中,
OA2=OB2+AB2,即r2=(r﹣2)2+32,
解得r=cm.
故答案为:.
点评:
本题考查的是垂径定理的应用,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
11.工程上常用钢珠来测量零件上小圆孔的宽口,假设钢珠的直径是10mm,测得钢珠顶端离零件表面的距离为8mm,如图所示,则这个小圆孔的宽口AB的长度为 8 mm.
考点:
垂径定理的应用;勾股定理.
专题:
探究型.
分析:
先求出钢珠的半径及OD的长,连接OA,过点O作OD⊥AB于点D,则AB=2AD,在Rt△AOD中利用勾股定理即可求出AD的长,进而得出AB的长.
解答:
解:连接OA,过点O作OD⊥AB于点D,则AB=2AD,
∵钢珠的直径是10mm,
∴钢珠的半径是5mm,
∵钢珠顶端离零件表面的距离为8mm,
∴OD=3mm,
在Rt△AOD中,
∵AD===4mm,
∴AB=2AD=2×4=8mm.
故答案为:8.
点评:
本题考查的是垂径定理的应用及勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
12.如图,将⊙O沿弦AB折叠,使经过圆心O,则∠OAB= 30° .
考点:
垂径定理;等边三角形的判定与性质;翻折变换(折叠问题).
专题:
探究型.
分析:
过点O作OC⊥AB于点D,交⊙O于点C,再由将⊙O沿弦AB折叠,使经过圆心O可知,OD=OC,故可得出OD=OA,再由OC⊥AB即可得出结论.
解答:
解:过点O作OC⊥AB于点D,交⊙O于点C,
∵将⊙O沿弦AB折叠,使经过圆心O,
∴OD=OC,
∴OD=OA,
∵OC⊥AB,
∴∠OAB=30°.
故答案为;30°.
点评:
本题考查的是垂径定理及图形的反折变换,熟知图形反折不变性的性质是解答此题的关键.
13.如图,AB是⊙O的直径,CD是⊙O的弦,AB、CD的延长线交于E点,若AB=2DE,∠E=18°,则∠AOC的度数为 54 度.
考点:
三角形的外角性质;等腰三角形的性质;圆的认识.
专题:
压轴题.
分析:
根据AB=2DE得DE等于圆的半径,在△EDO和△CEO中,根据三角形的一个外角等于和它不相邻的两个内角的和求解.
解答:
解:连接OD,∵AB=2DE,
∴OD=DE,
∴∠E=∠EOD,
在△EDO中,∠ODC=∠E+∠EOD=36°,
∵OC=OD,
∴∠OCD=∠ODC=36°,
在△CEO中,∠AOC=∠E+∠OCD=18°+36°=54°.
点评:
本题主要利用三角形的外角性质求解.
14.如图,正方形ABCD的边长为2,E、F、G、H分别为各边中点,EG、FH相交于点O,以O为圆心,OE为半径画圆,则图中阴影部分的面积为 .
考点:
圆的认识.
分析:
图中阴影部分的面积为一个半圆,根据圆的面积公式计算即可.
解答:
解:由题意可得:OE=1,
阴影面积==.
点评:
本题主要考查了圆的面积公式.
三.解答题(共10小题)
15.如图所示,该小组发现8米高旗杆DE的影子EF落在了包含一圆弧型小桥在内的路上,于是他们开展了测算小桥所在圆的半径的活动.小刚身高1.6米,测得其影长为2.4米,同时测得EG的长为3米,HF的长为1米,测得拱高(弧GH的中点到弦GH的距离,即MN的长)为2米,求小桥所在圆的半径.
考点:
垂径定理的应用;勾股定理;相似三角形的应用.
分析:
根据已知得出旗杆高度,进而得出GM=MH,再利用勾股定理求出半径即可.
解答:
解:∵小刚身高1.6米,测得其影长为2.4米,
∴8米高旗杆DE的影子为:12m,
∵测得EG的长为3米,HF的长为1米,
∴GH=12﹣3﹣1=8(m),
∴GM=MH=4m.
如图,设小桥的圆心为O,连接OM、OG.
设小桥所在圆的半径为r,
∵MN=2m,
∴OM=(r﹣2)m.
在Rt△OGM中,由勾股定理得:
∴OG2=OM2+42,
∴r2=(r﹣2)2+16,
解得:r=5,
答:小桥所在圆的半径为5m.
点评:
此题主要考查了垂径定理以及勾股定理的应用,根据已知得出关于r的等式是解题关键.
16.如图,在同一平面内,有一组平行线l1、l2、l3,相邻两条平行线之间的距离均为4,点O在直线l1上,⊙O与直线l3的交点为A、B,AB=12,求⊙O的半径.
考点:
垂径定理;平行线之间的距离;勾股定理.
专题:
压轴题;探究型.
分析:
连接OA,过点O作OD⊥AB,由垂径定理可知AD=AB,再根据相邻两条平行线之间的距离均为4可知OD=4,在Rt△AOD中利用勾股定理即可求出OA的长.
解答:
解:连接OA,过点O作OD⊥AB,
∵AB=12,
∴AD=AB=×12=6,
∵相邻两条平行线之间的距离均为4,
∴OD=8,
在Rt△AOD中,
∵AD=6,OD=8,
∴OA===10.
答:⊙O的半径为:10.
点评:
本题考查的是垂径定理及勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
17.如图,⊙O的半径为17cm,弦AB∥CD,AB=30cm,CD=16cm,圆心O位于AB,CD的上方,求AB和CD的距离.
考点:
垂径定理;勾股定理.
专题:
探究型.
分析:
过点O作弦AB的垂线,垂足为E,延长AE交CD于点F,连接OA,OC;由于AB∥CD,则OF⊥CD,EF即为AB、CD间的距离;由垂径定理,易求得AE、CF的长,可连接OA、ODC在构建的直角三角形中,根据勾股定理即可求出OE、OF的长,也就求出了EF的长,即弦AB、CD间的距离.
解答:
解:过点O作弦AB的垂线,垂足为E,延长OE交CD于点F,连接OA,OC,
∵AB∥CD,
∴OF⊥CD,
∵AB=30cm,CD=16cm,
∴AE=AB=×30=15cm,CF=CD=×16=8cm,
在Rt△AOE中,
OE===8cm,
在Rt△OCF中,
OF===15cm,
∴EF=OF﹣OE=15﹣8=7cm.
答:AB和CD的距离为7cm.
点评:
本题考查的是勾股定理及垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
18.机器人“海宝”在某圆形区域表演“按指令行走”,如图所示,“海宝”从圆心O出发,先沿北偏西67.4°方向行走13米至点A处,再沿正南方向行走14米至点B处,最后沿正东方向行走至点C处,点B、C都在圆O上.
(1)求弦BC的长;(2)求圆O的半径长.
(本题参考数据:sin67.4°=,cos67.4°=,tan67.4°=)
考点:
解直角三角形的应用-方向角问题;勾股定理;垂径定理.
分析:
(1)过O作OD⊥AB于D,则∠AOB=90°﹣67.4°=22.6°.在Rt△AOD中,利用∠AOB的三角函数值即可求出OD,AD的长;
(2)求出BD的长,根据勾股定理即可求出BO的长.
解答:
解:(1)连接OB,过点O作OD⊥AB,
∵AB∥SN,∠AON=67.4°,
∴∠A=67.4°.
∴OD=AO sin
67.4°=13×=12.
又∵BE=OD,
∴BE=12.
根据垂径定理,BC=2×12=24(米).
(2)∵AD=AO cos
67.4°=13×=5,
∴OD==12,
BD=AB﹣AD=14﹣5=9.
∴BO==15.
故圆O的半径长15米.
点评:
(1)将解直角三角形和勾股定理的应用相结合,求出BE,再根据垂径定理求出BC的长即可,有一定的综合性;
(2)利用(1)的结论,再根据勾股定理,即可求出半径.
19.如图,平面直角坐标系中,以点C(2,)为圆心,以2为半径的圆与x轴交于A,B两点.
(1)求A,B两点的坐标;
(2)若二次函数y=x2+bx+c的图象经过点A,B,试确定此二次函数的解析式.
考点:
垂径定理;待定系数法求二次函数解析式;勾股定理.
专题:
计算题.
分析:
(1)连结AC,过点C作CM⊥x轴于点M,根据垂径定理得MA=MB;由C点坐标得到OM=2,CM=,再根据勾股定理可计算出AM,可可计算出OA、OB,然后写出A,B两点的坐标;
(2)利用待定系数法求二次函数的解析式.
解答:
解:(1)过点C作CM⊥x轴于点M,则MA=MB,连结AC,如图
∵点C的坐标为(2,),
∴OM=2,CM=,
在Rt△ACM中,CA=2,
∴AM==1,
∴OA=OM﹣AM=1,OB=OM+BM=3,
∴A点坐标为(1,0),B点坐标为(3,0);
(2)将A(1,0),B(3,0)代入y=x2+bx+c得
,
解得.
所以二次函数的解析式为y=x2﹣4x+3.
点评:
本题考查了垂径定理:垂直于弦的直径平分弦,并且平分弦所对的弧.也考查了勾股定理和待定系数法求二次函数的解析式.
20.如图,是一个匀速旋转(指每分钟旋转的弧长或圆心角相同)的摩天轮的示意图,O为圆心,AB为水平地面,假设摩天轮的直径为80米,最低点C离地面为6米,旋转一周所用的时间为6分钟,小明从点C乘坐摩天轮(身高忽略不计),请问:
(1)经过2分钟后,小明离开地面的高度大约是多少米?
(2)若小明到了最高点,在视线没有阻挡的情况下能看到周围3公里远的地面景物,则他看到的地面景物有多大面积?(精确到1平方公里)
考点:
解直角三角形的应用;勾股定理;圆心角、弧、弦的关系.
分析:
(1)延长CO与圆交于点F,作EG⊥OF于点G.根据旋转一周所用的时间为6分钟,小明从点C乘坐摩天轮经过2分钟,可知∠COE=120°,根据平角的定义可知∠GOE=60°.根据三角函数可求出OG的长,小明离开地面的高度=OG+OC+CD可求.
(2)根据圆的面积公式可求.
解答:
解:(1)从点C乘坐摩天轮,经过2分钟后到达点E,(1分)
则∠COE=120°.
(2分)
延长CO与圆交于点F,作EG⊥OF于点G,(3分)
则∠GOE=60°.
(4分)
在Rt△EOG中,OG=40cos60°=20.
(5分)
∴小明2分钟后离开地面高度DG=DC+CO+OG=66米.
(6分)
(2)F为最高点,也能看到的地面景物面积为:
∵总高度86米=0.086km,
∴.
(8分)
注:若理解为s=32π=28平方公里不扣分,不写这句不扣分.
点评:
构造直角三角形,运用三角函数求出OG的长度是解题的关键.
21.如图,台风中心位于点P,并沿东北方向PQ移动,已知台风移动的速度为40千米/时,受影响区域的半径为260千米,B市位于点P的北偏东75°方向上,距离P点480千米.
(1)说明本次台风是否会影响B市;
(2)若这次台风会影响B市,求B市受台风影响的时间.
考点:
勾股定理;垂径定理的应用.
专题:
压轴题.
分析:
(1)作BH⊥PQ于点H,在Rt△BHP中,利用特殊角的三角函数值求出BH的长与260千米相比较即可.
(2)以B为圆心,以260为半径作圆交PQ于P1、P2两点,根据垂径定理即可求出P1P2的长,进而求出台风影响B市的时间.
解答:
解:(1)作BH⊥PQ于点H.
在Rt△BHP中,
由条件知,PB=480,∠BPQ=75°﹣45°=30°,
∴BH=480sin30°=240<260,
∴本次台风会影响B市.
(2)如图,若台风中心移动到P1时,台风开始影响B市,台风中心移动到P2时,台风影响结束.
由(1)得BH=240,由条件得BP1=BP2=260,
∴P1P2=2=200,
∴台风影响的时间t==5(小时).
故B市受台风影响的时间为5小时.
点评:
本题考查的是直角三角形的性质及垂径定理在实际生活中的运用,解答此题的关键是构造出直角三角形及圆.
22.如图,将一个两边都带有刻度的直尺放在半圆形纸片上,使其一边经过圆心O,另一边所在直线与半圆相交于点D,E,量出半径OC=5cm,弦DE=8cm,求直尺的宽.
考点:
垂径定理的应用;勾股定理.
分析:
过点O作OM⊥DE于点M,连接OD.
根据垂径定理“垂直于弦的直径平分弦,并且平分弦所对的两条弧”和勾股定理进行计算.
解答:
解:过点O作OM⊥DE于点M,连接OD.
∴DM=.
∵DE=8(cm)
∴DM=4(cm)
在Rt△ODM中,∵OD=OC=5(cm),
∴OM===3(cm)
∴直尺的宽度为3cm.
点评:
综合运用了垂径定理和勾股定理.
23.如图是一个半圆形桥洞截面示意图,圆心为O,直径AB是河底线,弦CD是水位线,CD∥AB,且CD=24
m,OE⊥CD于点E.已测得sin∠DOE=.
(1)求半径OD;
(2)根据需要,水面要以每小时0.5
m的速度下降,则经过多长时间才能将水排干?
考点:
垂径定理的应用;勾股定理.
专题:
应用题;压轴题.
分析:
根据三角函数可得到OD的值;再根据勾股定理求得OE的值,此时再求所需的时间就变得容易了.
解答:
解:(1)∵OE⊥CD于点E,CD=24,
∴ED=CD=12,
在Rt△DOE中,
∵sin∠DOE==,
∴OD=13(m);
(2)OE===5,
∴将水排干需:5÷0.5=10(小时).
点评:
此题主要考查了学生对垂径定理及勾股定理的运用.
一.选择题(共8小题)
1.如图,直线l1∥l2,点A在直线l1上,以点A为圆心,适当长为半径画弧,分别交直线l1、l2于B、C两点,连接AC、BC.若∠ABC=54°,则∠1的大小为( )
(1题)
(2题)
A.
36°
B.
54°
C.
72°
D.
73°
2.
CD是⊙O的一条弦,作直径AB,使AB⊥CD,垂足为E,若AB=10,CD=8,则BE的长是( )
A.
8
B.
2
C.
2或8
D.
3或7
3.如图,圆心在y轴的负半轴上,半径为5的⊙B与y轴的正半轴交于点A(0,1),过点P(0,﹣7)的直线l与⊙B相交于C,D两点.则弦CD长的所有可能的整数值有( )
A.
1个
B.
2个
C.
3个
D.
4个
4.如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB交于点D,则AD的长为( )
(4题)
(5题)
A.
B.
C.
D.
5.小英家的圆形镜子被打碎了,她拿了如图(网格中的每个小正方形边长为1)的一块碎片到玻璃店,配制成形状、大小与原来一致的镜面,则这个镜面的半径是( )
A.
2
B.
C.
2
D.
3
6.在圆柱形油槽内装有一些油.截面如图,油面宽AB为6分米,如果再注入一些油后,油面AB上升1分米,油面宽变为8分米,圆柱形油槽直径MN为( )
(6题)
(7题)
A.
6分米
B.
8分米
C.
10分米
D.
12分米
7.如图所示,在⊙O中,,∠A=30°,则∠B=( )
A.
150°
B.
75°
C.
60°
D.
15°
8.如图,已知⊙O的两条弦AC,BD相交于点E,∠A=70°,∠c=50°,那么sin∠AEB的值为( )
(8题)
(9题)
(10题)
A.
B.
C.
D.
二.填空题(共6小题)
9.如图,⊙O的半径为1cm,弦AB、CD的长度分别为cm,1cm,则弦AC、BD所夹的锐角α= _________ 度.
10.如图,一个宽为2厘米的刻度尺(刻度单位:厘米),放在圆形玻璃杯的杯口上,刻度尺的一边与杯口外沿相切,另一边与杯口外沿两个交点处的读数恰好是3和9,那么玻璃杯的杯口外沿半径为 _________ 厘米.
11.工程上常用钢珠来测量零件上小圆孔的宽口,假设钢珠的直径是10mm,测得钢珠顶端离零件表面的距离为8mm,如图所示,则这个小圆孔的宽口AB的长度为 _________ mm.
(11题)
(12题)
(13题)
(14题)
12.如图,将⊙O沿弦AB折叠,使经过圆心O,则∠OAB= _________ .
13.如图,AB是⊙O的直径,CD是⊙O的弦,AB、CD的延长线交于E点,若AB=2DE,∠E=18°,则∠AOC的度数为 _________ 度.
14.如图,正方形ABCD的边长为2,E、F、G、H分别为各边中点,EG、FH相交于点O,以O为圆心,OE为半径画圆,则图中阴影部分的面积为 _________ .
三.解答题(共10小题)
15.如图所示,该小组发现8米高旗杆DE的影子EF落在了包含一圆弧型小桥在内的路上,于是他们开展了测算小桥所在圆的半径的活动.小刚身高1.6米,测得其影长为2.4米,同时测得EG的长为3米,HF的长为1米,测得拱高(弧GH的中点到弦GH的距离,即MN的长)为2米,求小桥所在圆的半径.
16.如图,在同一平面内,有一组平行线l1、l2、l3,相邻两条平行线之间的距离均为4,点O在直线l1上,⊙O与直线l3的交点为A、B,AB=12,求⊙O的半径.
17.如图,⊙O的半径为17cm,弦AB∥CD,AB=30cm,CD=16cm,圆心O位于AB,CD的上方,求AB和CD的距离.
18.机器人“海宝”在某圆形区域表演“按指令行走”,如图所示,“海宝”从圆心O出发,先沿北偏西67.4°方向行走13米至点A处,再沿正南方向行走14米至点B处,最后沿正东方向行走至点C处,点B、C都在圆O上.
(1)求弦BC的长;(2)求圆O的半径长.(本题参考数据:sin67.4°=,cos67.4°=,tan67.4°=)
19.如图,平面直角坐标系中,以点C(2,)为圆心,以2为半径的圆与x轴交于A,B两点.
(1)求A,B两点的坐标;
(2)若二次函数y=x2+bx+c的图象经过点A,B,试确定此二次函数的解析式.
20.如图,是一个匀速旋转(指每分钟旋转的弧长或圆心角相同)的摩天轮的示意图,O为圆心,AB为水平地面,假设摩天轮的直径为80米,最低点C离地面为6米,旋转一周所用的时间为6分钟,小明从点C乘坐摩天轮(身高忽略不计),请问:
(1)经过2分钟后,小明离开地面的高度大约是多少米?
(2)若小明到了最高点,在视线没有阻挡的情况下能看到周围3公里远的地面景物,则他看到的地面景物有多大面积?(精确到1平方公里)
21.如图,台风中心位于点P,并沿东北方向PQ移动,已知台风移动的速度为40千米/时,受影响区域的半径为260千米,B市位于点P的北偏东75°方向上,距离P点480千米.
(1)说明本次台风是否会影响B市;
(2)若这次台风会影响B市,求B市受台风影响的时间.
22.如图,将一个两边都带有刻度的直尺放在半圆形纸片上,使其一边经过圆心O,另一边所在直线与半圆相交于点D,E,量出半径OC=5cm,弦DE=8cm,求直尺的宽.
23.如图是一个半圆形桥洞截面示意图,圆心为O,直径AB是河底线,弦CD是水位线,CD∥AB,且CD=24
m,OE⊥CD于点E.已测得sin∠DOE=.
(1)求半径OD;
(2)根据需要,水面要以每小时0.5
m的速度下降,则经过多长时间才能将水排干?
27.1.2圆的对称性2
参考答案与试题解析
一.选择题(共8小题)
1.如图,直线l1∥l2,点A在直线l1上,以点A为圆心,适当长为半径画弧,分别交直线l1、l2于B、C两点,连接AC、BC.若∠ABC=54°,则∠1的大小为( )
A.
36°
B.
54°
C.
72°
D.
73°
考点:
平行线的性质;圆的认识.
专题:
压轴题.
分析:
由l1∥l2,∠ABC=54°,根据两直线平行,内错角相等,即可求得∠2的度数,又由以点A为圆心,适当长为半径画弧,分别交直线l1、l2于B、C两点,连接AC、BC,可得AC=AB,即可证得∠ACB=∠ABC=54°,然后由平角的定义即可求得答案.
解答:
解:∵l1∥l2,∠ABC=54°,
∴∠2=∠ABC=54°,
∵以点A为圆心,适当长为半径画弧,分别交直线l1、l2于B、C两点,
∴AC=AB,
∴∠ACB=∠ABC=54°,
∵∠1+∠ACB+∠2=180°,
∴∠1=72°.
故选C.
点评:
此题考查了平行线的性质与等腰三角形的性质,以及平角的定义.注意两直线平行,内错角相等.
2.CD是⊙O的一条弦,作直径AB,使AB⊥CD,垂足为E,若AB=10,CD=8,则BE的长是( )
A.
8
B.
2
C.
2或8
D.
3或7
考点:
垂径定理;勾股定理.
专题:
计算题.
分析:
连结OC,根据垂径定理得到CE=4,再根据勾股定理计算出OE=3,分类讨论:当点E在半径OB上时,BE=OB﹣OE;当点E在半径OA上时,BE=OB+OE,然后把CE、OE的值代入计算即可.
解答:
解:如图,连结OC,
∵直径AB⊥CD,
∴CE=DE=CD=×8=4,
在Rt△OCE中,OC=AB=5,
∴OE==3,
当点E在半径OB上时,BE=OB﹣OE=5﹣3=2,
当点E在半径OA上时,BE=OB+OE=5+3=8,
∴BE的长为2或8.
故选C.
点评:
本题考查了垂径定理:平分弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了勾股定理.
3.如图,圆心在y轴的负半轴上,半径为5的⊙B与y轴的正半轴交于点A(0,1),过点P(0,﹣7)的直线l与⊙B相交于C,D两点.则弦CD长的所有可能的整数值有( )
A.
1个
B.
2个
C.
3个
D.
4个
考点:
垂径定理;坐标与图形性质;勾股定理.
专题:
压轴题.
分析:
求出线段CD的最小值,及线段CD的最大值,从而可判断弦CD长的所有可能的整数值.
解答:
解:∵点A的坐标为(0,1),圆的半径为5,
∴点B的坐标为(0,﹣4),
又∵点P的坐标为(0,﹣7),
∴BP=3,
①当CD垂直圆的直径AE时,CD的值最小,
连接BC,在Rt△BCP中,CP==4;
故CD=2CP=8,
②当CD经过圆心时,CD的值最大,此时CD=直径AE=10;
所以,8≤CD≤10,
综上可得:弦CD长的所有可能的整数值有:8,9,10,共3个.
故选C.
点评:
本题考查了垂径定理的知识,解答本题的关键是熟练掌握垂直弦的直径平分弦,本题需要讨论两个极值点,有一定难度.
4.如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB交于点D,则AD的长为( )
A.
B.
C.
D.
考点:
垂径定理;勾股定理.
专题:
探究型.
分析:
先根据勾股定理求出AB的长,过C作CM⊥AB,交AB于点M,由垂径定理可知M为AD的中点,由三角形的面积可求出CM的长,在Rt△ACM中,根据勾股定理可求出AM的长,进而可得出结论.
解答:
解:∵在Rt△ABC中,∠ACB=90°,AC=3,BC=4,
∴AB===5,
过C作CM⊥AB,交AB于点M,如图所示,
∵CM⊥AB,
∴M为AD的中点,
∵S△ABC=AC BC=AB CM,且AC=3,BC=4,AB=5,
∴CM=,
在Rt△ACM中,根据勾股定理得:AC2=AM2+CM2,即9=AM2+()2,
解得:AM=,
∴AD=2AM=.
故选C.
点评:
本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
5.小英家的圆形镜子被打碎了,她拿了如图(网格中的每个小正方形边长为1)的一块碎片到玻璃店,配制成形状、大小与原来一致的镜面,则这个镜面的半径是( )
A.
2
B.
C.
2
D.
3
考点:
垂径定理的应用;勾股定理.
专题:
网格型.
分析:
在网格中找点A、B、D(如图),作AB,BD的中垂线,交点O就是圆心,故OA即为此圆的半径,根据勾股定理求出OA的长即可.
解答:
解:如图所示,作AB,BD的中垂线,交点O就是圆心.
连接OA、OB,
∵OC⊥AB,OA=OB
∴O即为此圆形镜子的圆心,
∵AC=1,OC=2,
∴OA===.
故选B.
点评:
本题考查的是垂径定理在实际生活中的运用,根据题意构造出直角三角形是解答此题的关键.
6.在圆柱形油槽内装有一些油.截面如图,油面宽AB为6分米,如果再注入一些油后,油面AB上升1分米,油面宽变为8分米,圆柱形油槽直径MN为( )
A.
6分米
B.
8分米
C.
10分米
D.
12分米
考点:
垂径定理的应用.
专题:
压轴题.
分析:
如图,油面AB上升1分米得到油面CD,依题意得AB=6,CD=8,过O点作AB的垂线,垂足为E,交CD于F点,连接OA,OC,由垂径定理,得AE=AB=3,CF=CD=4,设OE=x,则OF=x﹣1,在Rt△OAE中,OA2=AE2+OE2,在Rt△OCF中,OC2=CF2+OF2,由OA=OC,列方程求x即可求半径OA,得出直径MN.
解答:
解:如图,依题意得AB=6,CD=8,过O点作AB的垂线,垂足为E,交CD于F点,连接OA,OC,
由垂径定理,得AE=AB=3,CF=CD=4,
设OE=x,则OF=x﹣1,
在Rt△OAE中,OA2=AE2+OE2,
在Rt△OCF中,OC2=CF2+OF2,
∵OA=OC,
∴32+x2=42+(x﹣1)2,
解得x=4,
∴半径OA==5,
∴直径MN=2OA=10分米.
故选C.
点评:
本题考查了垂径定理的运用.关键是利用垂径定理得出两个直角三角形,根据勾股定理表示半径的平方,根据半径相等列方程求解.
7.如图所示,在⊙O中,,∠A=30°,则∠B=( )
A.
150°
B.
75°
C.
60°
D.
15°
考点:
圆心角、弧、弦的关系.
分析:
先根据等弧所对的弦相等求得AB=AC,从而判定△ABC是等腰三角形;然后根据等腰三角形的两个底角相等得出∠B=∠C;最后由三角形的内角和定理求角B的度数即可.
解答:
解:∵在⊙O中,,
∴AB=AC,
∴△ABC是等腰三角形,
∴∠B=∠C;
又∠A=30°,
∴∠B==75°(三角形内角和定理).
故选B.
点评:
本题综合考查了圆心角、弧、弦的关系,以及等腰三角形的性质.解题的关键是根据等弧对等弦推知△ABC是等腰三角形.
8.如图,已知⊙O的两条弦AC,BD相交于点E,∠A=70°,∠c=50°,那么sin∠AEB的值为( )
A.
B.
C.
D.
考点:
特殊角的三角函数值;三角形内角和定理;圆心角、弧、弦的关系.
分析:
根据三角形的内角和是180°求得∠AEB的度数,再根据特殊角的锐角三角函数值求解.
解答:
解:∵∠A=70°,∠C=50°,
∴∠B=∠C=50°,∠AEB=60°,
∴sin∠AEB=.
故选D.
点评:
考查了圆周角定理、三角形的内角和是180°,还要熟记特殊角的锐角三角函数值.
二.填空题(共6小题)
9.如图,⊙O的半径为1cm,弦AB、CD的长度分别为cm,1cm,则弦AC、BD所夹的锐角α= 75 度.
考点:
圆心角、弧、弦的关系;三角形的外角性质;勾股定理;垂径定理.
专题:
压轴题.
分析:
根据勾股定理的逆定理可证△AOB是等腰直角三角形,故可求∠OAB=∠OBA=45°,又由已知可证△COD是等边三角形,所以∠ODC=∠OCD=60°,根据圆周角的性质可证∠CDB=∠CAB,而∠ODB=∠OBD,所以∠CAB+∠OBD=∠CDB+∠ODB=∠ODC=60°,再根据三角形的内角和定理可求α.
解答:
解:连接OA、OB、OC、OD,
∵OA=OB=OC=OD=1,AB=,CD=1,
∴OA2+OB2=AB2,
∴△AOB是等腰直角三角形,
△COD是等边三角形,
∴∠OAB=∠OBA=45°,∠ODC=∠OCD=60°,
∵∠CDB=∠CAB,∠ODB=∠OBD,
∴α=180°﹣∠CAB﹣∠OBA﹣∠OBD=180°﹣∠OBA﹣(∠CDB+∠ODB)=180°﹣45°﹣60°=75°.
点评:
本题考查了勾股定理的逆定理,圆周角的性质,等边三角形的性质以及三角形的内角和定理.
10.如图,一个宽为2厘米的刻度尺(刻度单位:厘米),放在圆形玻璃杯的杯口上,刻度尺的一边与杯口外沿相切,另一边与杯口外沿两个交点处的读数恰好是3和9,那么玻璃杯的杯口外沿半径为 厘米.
考点:
垂径定理的应用;勾股定理.
专题:
压轴题.
分析:
先求出弦AC的长,再过点O作OB⊥AC于点B,由垂径定理可得出AB的长,设杯口的半径为r,则OB=r﹣2,OA=r,在Rt△AOB中根据勾股定理求出r的值即可.
解答:
解:∵杯口外沿两个交点处的读数恰好是3和9,
∴AC=9﹣3=6,
过点O作OB⊥AC于点B,则AB=AC=×6=3cm,
设杯口的半径为r,则OB=r﹣2,OA=r,
在Rt△AOB中,
OA2=OB2+AB2,即r2=(r﹣2)2+32,
解得r=cm.
故答案为:.
点评:
本题考查的是垂径定理的应用,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
11.工程上常用钢珠来测量零件上小圆孔的宽口,假设钢珠的直径是10mm,测得钢珠顶端离零件表面的距离为8mm,如图所示,则这个小圆孔的宽口AB的长度为 8 mm.
考点:
垂径定理的应用;勾股定理.
专题:
探究型.
分析:
先求出钢珠的半径及OD的长,连接OA,过点O作OD⊥AB于点D,则AB=2AD,在Rt△AOD中利用勾股定理即可求出AD的长,进而得出AB的长.
解答:
解:连接OA,过点O作OD⊥AB于点D,则AB=2AD,
∵钢珠的直径是10mm,
∴钢珠的半径是5mm,
∵钢珠顶端离零件表面的距离为8mm,
∴OD=3mm,
在Rt△AOD中,
∵AD===4mm,
∴AB=2AD=2×4=8mm.
故答案为:8.
点评:
本题考查的是垂径定理的应用及勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
12.如图,将⊙O沿弦AB折叠,使经过圆心O,则∠OAB= 30° .
考点:
垂径定理;等边三角形的判定与性质;翻折变换(折叠问题).
专题:
探究型.
分析:
过点O作OC⊥AB于点D,交⊙O于点C,再由将⊙O沿弦AB折叠,使经过圆心O可知,OD=OC,故可得出OD=OA,再由OC⊥AB即可得出结论.
解答:
解:过点O作OC⊥AB于点D,交⊙O于点C,
∵将⊙O沿弦AB折叠,使经过圆心O,
∴OD=OC,
∴OD=OA,
∵OC⊥AB,
∴∠OAB=30°.
故答案为;30°.
点评:
本题考查的是垂径定理及图形的反折变换,熟知图形反折不变性的性质是解答此题的关键.
13.如图,AB是⊙O的直径,CD是⊙O的弦,AB、CD的延长线交于E点,若AB=2DE,∠E=18°,则∠AOC的度数为 54 度.
考点:
三角形的外角性质;等腰三角形的性质;圆的认识.
专题:
压轴题.
分析:
根据AB=2DE得DE等于圆的半径,在△EDO和△CEO中,根据三角形的一个外角等于和它不相邻的两个内角的和求解.
解答:
解:连接OD,∵AB=2DE,
∴OD=DE,
∴∠E=∠EOD,
在△EDO中,∠ODC=∠E+∠EOD=36°,
∵OC=OD,
∴∠OCD=∠ODC=36°,
在△CEO中,∠AOC=∠E+∠OCD=18°+36°=54°.
点评:
本题主要利用三角形的外角性质求解.
14.如图,正方形ABCD的边长为2,E、F、G、H分别为各边中点,EG、FH相交于点O,以O为圆心,OE为半径画圆,则图中阴影部分的面积为 .
考点:
圆的认识.
分析:
图中阴影部分的面积为一个半圆,根据圆的面积公式计算即可.
解答:
解:由题意可得:OE=1,
阴影面积==.
点评:
本题主要考查了圆的面积公式.
三.解答题(共10小题)
15.如图所示,该小组发现8米高旗杆DE的影子EF落在了包含一圆弧型小桥在内的路上,于是他们开展了测算小桥所在圆的半径的活动.小刚身高1.6米,测得其影长为2.4米,同时测得EG的长为3米,HF的长为1米,测得拱高(弧GH的中点到弦GH的距离,即MN的长)为2米,求小桥所在圆的半径.
考点:
垂径定理的应用;勾股定理;相似三角形的应用.
分析:
根据已知得出旗杆高度,进而得出GM=MH,再利用勾股定理求出半径即可.
解答:
解:∵小刚身高1.6米,测得其影长为2.4米,
∴8米高旗杆DE的影子为:12m,
∵测得EG的长为3米,HF的长为1米,
∴GH=12﹣3﹣1=8(m),
∴GM=MH=4m.
如图,设小桥的圆心为O,连接OM、OG.
设小桥所在圆的半径为r,
∵MN=2m,
∴OM=(r﹣2)m.
在Rt△OGM中,由勾股定理得:
∴OG2=OM2+42,
∴r2=(r﹣2)2+16,
解得:r=5,
答:小桥所在圆的半径为5m.
点评:
此题主要考查了垂径定理以及勾股定理的应用,根据已知得出关于r的等式是解题关键.
16.如图,在同一平面内,有一组平行线l1、l2、l3,相邻两条平行线之间的距离均为4,点O在直线l1上,⊙O与直线l3的交点为A、B,AB=12,求⊙O的半径.
考点:
垂径定理;平行线之间的距离;勾股定理.
专题:
压轴题;探究型.
分析:
连接OA,过点O作OD⊥AB,由垂径定理可知AD=AB,再根据相邻两条平行线之间的距离均为4可知OD=4,在Rt△AOD中利用勾股定理即可求出OA的长.
解答:
解:连接OA,过点O作OD⊥AB,
∵AB=12,
∴AD=AB=×12=6,
∵相邻两条平行线之间的距离均为4,
∴OD=8,
在Rt△AOD中,
∵AD=6,OD=8,
∴OA===10.
答:⊙O的半径为:10.
点评:
本题考查的是垂径定理及勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
17.如图,⊙O的半径为17cm,弦AB∥CD,AB=30cm,CD=16cm,圆心O位于AB,CD的上方,求AB和CD的距离.
考点:
垂径定理;勾股定理.
专题:
探究型.
分析:
过点O作弦AB的垂线,垂足为E,延长AE交CD于点F,连接OA,OC;由于AB∥CD,则OF⊥CD,EF即为AB、CD间的距离;由垂径定理,易求得AE、CF的长,可连接OA、ODC在构建的直角三角形中,根据勾股定理即可求出OE、OF的长,也就求出了EF的长,即弦AB、CD间的距离.
解答:
解:过点O作弦AB的垂线,垂足为E,延长OE交CD于点F,连接OA,OC,
∵AB∥CD,
∴OF⊥CD,
∵AB=30cm,CD=16cm,
∴AE=AB=×30=15cm,CF=CD=×16=8cm,
在Rt△AOE中,
OE===8cm,
在Rt△OCF中,
OF===15cm,
∴EF=OF﹣OE=15﹣8=7cm.
答:AB和CD的距离为7cm.
点评:
本题考查的是勾股定理及垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
18.机器人“海宝”在某圆形区域表演“按指令行走”,如图所示,“海宝”从圆心O出发,先沿北偏西67.4°方向行走13米至点A处,再沿正南方向行走14米至点B处,最后沿正东方向行走至点C处,点B、C都在圆O上.
(1)求弦BC的长;(2)求圆O的半径长.
(本题参考数据:sin67.4°=,cos67.4°=,tan67.4°=)
考点:
解直角三角形的应用-方向角问题;勾股定理;垂径定理.
分析:
(1)过O作OD⊥AB于D,则∠AOB=90°﹣67.4°=22.6°.在Rt△AOD中,利用∠AOB的三角函数值即可求出OD,AD的长;
(2)求出BD的长,根据勾股定理即可求出BO的长.
解答:
解:(1)连接OB,过点O作OD⊥AB,
∵AB∥SN,∠AON=67.4°,
∴∠A=67.4°.
∴OD=AO sin
67.4°=13×=12.
又∵BE=OD,
∴BE=12.
根据垂径定理,BC=2×12=24(米).
(2)∵AD=AO cos
67.4°=13×=5,
∴OD==12,
BD=AB﹣AD=14﹣5=9.
∴BO==15.
故圆O的半径长15米.
点评:
(1)将解直角三角形和勾股定理的应用相结合,求出BE,再根据垂径定理求出BC的长即可,有一定的综合性;
(2)利用(1)的结论,再根据勾股定理,即可求出半径.
19.如图,平面直角坐标系中,以点C(2,)为圆心,以2为半径的圆与x轴交于A,B两点.
(1)求A,B两点的坐标;
(2)若二次函数y=x2+bx+c的图象经过点A,B,试确定此二次函数的解析式.
考点:
垂径定理;待定系数法求二次函数解析式;勾股定理.
专题:
计算题.
分析:
(1)连结AC,过点C作CM⊥x轴于点M,根据垂径定理得MA=MB;由C点坐标得到OM=2,CM=,再根据勾股定理可计算出AM,可可计算出OA、OB,然后写出A,B两点的坐标;
(2)利用待定系数法求二次函数的解析式.
解答:
解:(1)过点C作CM⊥x轴于点M,则MA=MB,连结AC,如图
∵点C的坐标为(2,),
∴OM=2,CM=,
在Rt△ACM中,CA=2,
∴AM==1,
∴OA=OM﹣AM=1,OB=OM+BM=3,
∴A点坐标为(1,0),B点坐标为(3,0);
(2)将A(1,0),B(3,0)代入y=x2+bx+c得
,
解得.
所以二次函数的解析式为y=x2﹣4x+3.
点评:
本题考查了垂径定理:垂直于弦的直径平分弦,并且平分弦所对的弧.也考查了勾股定理和待定系数法求二次函数的解析式.
20.如图,是一个匀速旋转(指每分钟旋转的弧长或圆心角相同)的摩天轮的示意图,O为圆心,AB为水平地面,假设摩天轮的直径为80米,最低点C离地面为6米,旋转一周所用的时间为6分钟,小明从点C乘坐摩天轮(身高忽略不计),请问:
(1)经过2分钟后,小明离开地面的高度大约是多少米?
(2)若小明到了最高点,在视线没有阻挡的情况下能看到周围3公里远的地面景物,则他看到的地面景物有多大面积?(精确到1平方公里)
考点:
解直角三角形的应用;勾股定理;圆心角、弧、弦的关系.
分析:
(1)延长CO与圆交于点F,作EG⊥OF于点G.根据旋转一周所用的时间为6分钟,小明从点C乘坐摩天轮经过2分钟,可知∠COE=120°,根据平角的定义可知∠GOE=60°.根据三角函数可求出OG的长,小明离开地面的高度=OG+OC+CD可求.
(2)根据圆的面积公式可求.
解答:
解:(1)从点C乘坐摩天轮,经过2分钟后到达点E,(1分)
则∠COE=120°.
(2分)
延长CO与圆交于点F,作EG⊥OF于点G,(3分)
则∠GOE=60°.
(4分)
在Rt△EOG中,OG=40cos60°=20.
(5分)
∴小明2分钟后离开地面高度DG=DC+CO+OG=66米.
(6分)
(2)F为最高点,也能看到的地面景物面积为:
∵总高度86米=0.086km,
∴.
(8分)
注:若理解为s=32π=28平方公里不扣分,不写这句不扣分.
点评:
构造直角三角形,运用三角函数求出OG的长度是解题的关键.
21.如图,台风中心位于点P,并沿东北方向PQ移动,已知台风移动的速度为40千米/时,受影响区域的半径为260千米,B市位于点P的北偏东75°方向上,距离P点480千米.
(1)说明本次台风是否会影响B市;
(2)若这次台风会影响B市,求B市受台风影响的时间.
考点:
勾股定理;垂径定理的应用.
专题:
压轴题.
分析:
(1)作BH⊥PQ于点H,在Rt△BHP中,利用特殊角的三角函数值求出BH的长与260千米相比较即可.
(2)以B为圆心,以260为半径作圆交PQ于P1、P2两点,根据垂径定理即可求出P1P2的长,进而求出台风影响B市的时间.
解答:
解:(1)作BH⊥PQ于点H.
在Rt△BHP中,
由条件知,PB=480,∠BPQ=75°﹣45°=30°,
∴BH=480sin30°=240<260,
∴本次台风会影响B市.
(2)如图,若台风中心移动到P1时,台风开始影响B市,台风中心移动到P2时,台风影响结束.
由(1)得BH=240,由条件得BP1=BP2=260,
∴P1P2=2=200,
∴台风影响的时间t==5(小时).
故B市受台风影响的时间为5小时.
点评:
本题考查的是直角三角形的性质及垂径定理在实际生活中的运用,解答此题的关键是构造出直角三角形及圆.
22.如图,将一个两边都带有刻度的直尺放在半圆形纸片上,使其一边经过圆心O,另一边所在直线与半圆相交于点D,E,量出半径OC=5cm,弦DE=8cm,求直尺的宽.
考点:
垂径定理的应用;勾股定理.
分析:
过点O作OM⊥DE于点M,连接OD.
根据垂径定理“垂直于弦的直径平分弦,并且平分弦所对的两条弧”和勾股定理进行计算.
解答:
解:过点O作OM⊥DE于点M,连接OD.
∴DM=.
∵DE=8(cm)
∴DM=4(cm)
在Rt△ODM中,∵OD=OC=5(cm),
∴OM===3(cm)
∴直尺的宽度为3cm.
点评:
综合运用了垂径定理和勾股定理.
23.如图是一个半圆形桥洞截面示意图,圆心为O,直径AB是河底线,弦CD是水位线,CD∥AB,且CD=24
m,OE⊥CD于点E.已测得sin∠DOE=.
(1)求半径OD;
(2)根据需要,水面要以每小时0.5
m的速度下降,则经过多长时间才能将水排干?
考点:
垂径定理的应用;勾股定理.
专题:
应用题;压轴题.
分析:
根据三角函数可得到OD的值;再根据勾股定理求得OE的值,此时再求所需的时间就变得容易了.
解答:
解:(1)∵OE⊥CD于点E,CD=24,
∴ED=CD=12,
在Rt△DOE中,
∵sin∠DOE==,
∴OD=13(m);
(2)OE===5,
∴将水排干需:5÷0.5=10(小时).
点评:
此题主要考查了学生对垂径定理及勾股定理的运用.
