华师大版九年级数学下27.3.2圆锥的侧面积和全面积课文练习含答案解析
文档属性
| 名称 | 华师大版九年级数学下27.3.2圆锥的侧面积和全面积课文练习含答案解析 |  | |
| 格式 | zip | ||
| 文件大小 | 152.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-11-07 08:43:02 | ||
图片预览



文档简介
27.3.2圆锥的侧面积和全面积
一.选择题(共8小题)
1.已知圆锥的底面半径为2cm,母线长为5cm,则圆锥的侧面积是( )
A.10cm2
B.5π
cm2
C.10π
cm2
D.20π
cm2
2.已知圆锥的高为4,母线长为5,则该圆锥的表面积为( )
A.21π
B.15π
C.12π
D.24π
3.已知圆锥的母线长为6cm,底面圆的半径为3cm,则此圆锥侧面展开图的圆心角是( )
A.30°
B.60°
C.90°
D.180°
4.一个圆锥的侧面展开图是半径为6的半圆,则这个圆锥的底面半径为( )
A.1.5
B.2
C.2.5
D.3
5.如果圆锥的母线长为5cm,底面半径为2cm,那么这个圆锥的侧面积为( )
A.10cm2
B.10πcm2
C.20cm2
D.20πcm2
6.一个圆锥的底面半径是6cm,其侧面展开图为半圆,则圆锥的母线长为( )
A.9cm
B.12cm
C.15cm
D.18cm
7.如图,某同学用一扇形纸板为一个玩偶制作一个圆锥形帽子,已知扇形半径OA=13cm,扇形的弧长为10πcm,那么这个圆锥形帽子的高是( )cm.(不考虑接缝)
A.5
B.12
C.13
D.14
8.如图是一个几何体的三视图,则这个几何体的侧面积是( )
A.πcm2
B.2πcm2
C.6πcm2
D.3πcm2
二.填空题(共6小题)
9.圆锥的底面半径为6cm,母线长为10cm,则圆锥的侧面积为 _________ cm2.
10.一个底面直径是80cm,母线长为90cm的圆锥的侧面展开图的圆心角的度数为 _________ .
11.有一圆锥,它的高为8cm,底面半径为6cm,则这个圆锥的侧面积是 _________ cm2.(结果保留π)
12.圆锥的底面半径是2cm,母线长6cm,则这个圆锥侧面展开图的扇形圆心角度数为 _________ 度.
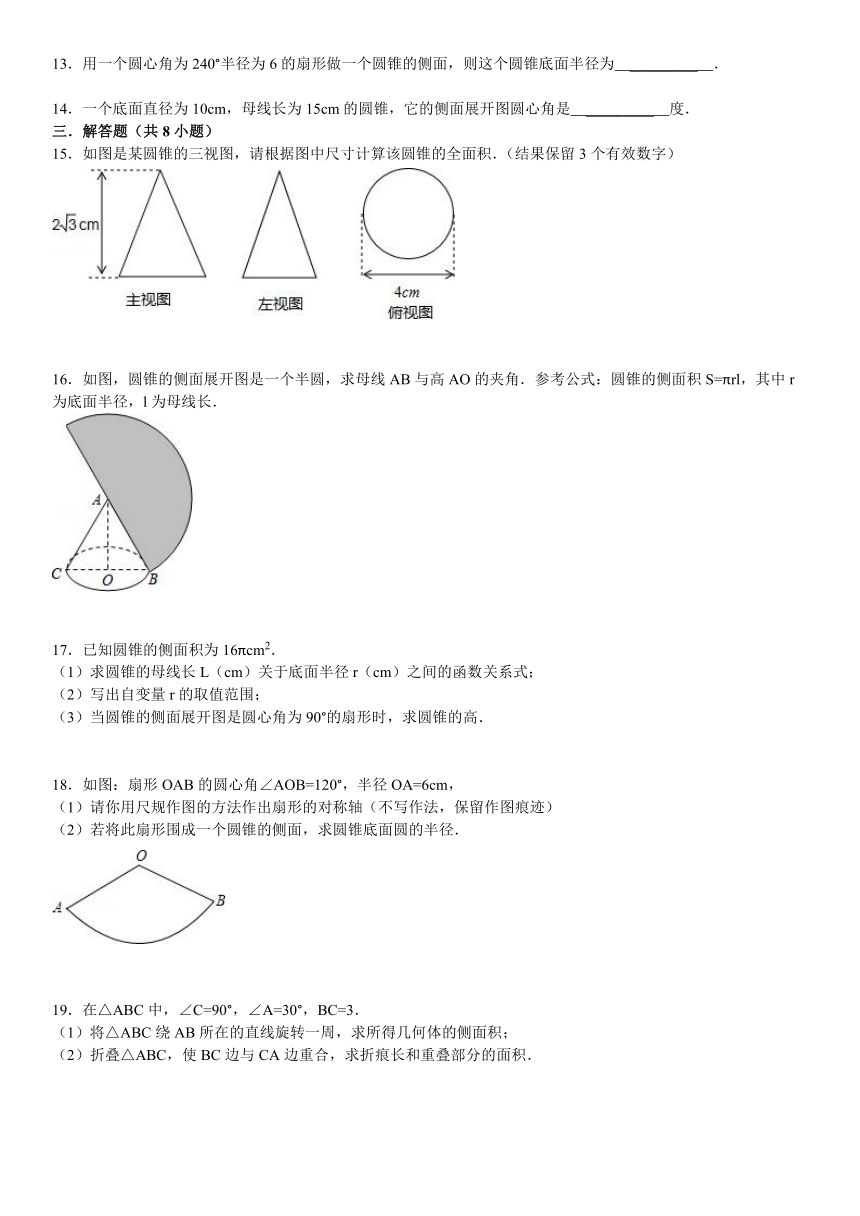
13.用一个圆心角为240°半径为6的扇形做一个圆锥的侧面,则这个圆锥底面半径为 _________ .
14.一个底面直径为10cm,母线长为15cm的圆锥,它的侧面展开图圆心角是 _________ 度.
三.解答题(共8小题)
15.如图是某圆锥的三视图,请根据图中尺寸计算该圆锥的全面积.(结果保留3个有效数字)
16.如图,圆锥的侧面展开图是一个半圆,求母线AB与高AO的夹角.参考公式:圆锥的侧面积S=πrl,其中r为底面半径,l为母线长.
17.已知圆锥的侧面积为16πcm2.
(1)求圆锥的母线长L(cm)关于底面半径r(cm)之间的函数关系式;
(2)写出自变量r的取值范围;
(3)当圆锥的侧面展开图是圆心角为90°的扇形时,求圆锥的高.
18.如图:扇形OAB的圆心角∠AOB=120°,半径OA=6cm,
(1)请你用尺规作图的方法作出扇形的对称轴(不写作法,保留作图痕迹)
(2)若将此扇形围成一个圆锥的侧面,求圆锥底面圆的半径.
19.在△ABC中,∠C=90°,∠A=30°,BC=3.
(1)将△ABC绕AB所在的直线旋转一周,求所得几何体的侧面积;
(2)折叠△ABC,使BC边与CA边重合,求折痕长和重叠部分的面积.
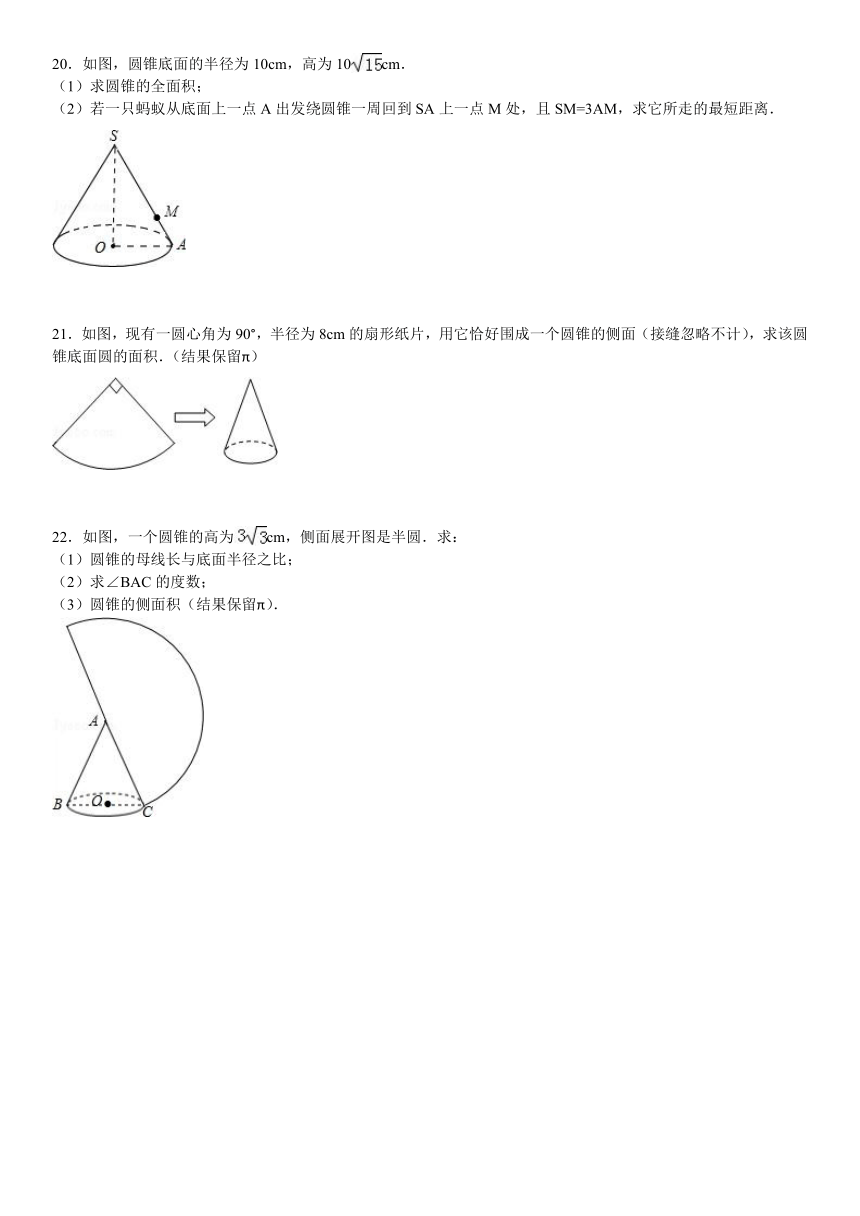
20.如图,圆锥底面的半径为10cm,高为10cm.
(1)求圆锥的全面积;
(2)若一只蚂蚁从底面上一点A出发绕圆锥一周回到SA上一点M处,且SM=3AM,求它所走的最短距离.
21.如图,现有一圆心角为90°,半径为8cm的扇形纸片,用它恰好围成一个圆锥的侧面(接缝忽略不计),求该圆锥底面圆的面积.(结果保留π)
22.如图,一个圆锥的高为cm,侧面展开图是半圆.求:
(1)圆锥的母线长与底面半径之比;
(2)求∠BAC的度数;
(3)圆锥的侧面积(结果保留π).
27.3.2圆锥的侧面积和全面积
参考答案与试题解析
一.选择题(共8小题)
1.已知圆锥的底面半径为2cm,母线长为5cm,则圆锥的侧面积是( )
A.
10cm2
B.5π
cm2
C.10π
cm2
D.
20π
cm2
考点:
圆锥的计算.
专题:
计算题.
分析:
根据圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和扇形的面积公式计算即可.
解答:
解:圆锥的侧面积= 2π 2 5=10π(cm2).
故选C.
点评:
本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.
2.已知圆锥的高为4,母线长为5,则该圆锥的表面积为( )
A.
21π
B.15π
C.12π
D.
24π
考点:
圆锥的计算.版权所有
分析:
首先根据勾股定理求得底面半径,则可以得到底面周长,然后利用扇形的面积公式即可求解.
解答:
解:底面半径是:=3,则底面周长是6π,
则圆锥的侧面积是:×6π×5=15π,底面积为9π,
则表面积为15π+9π=24π.
故选D.
点评:
考查了圆锥的计算.正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键,理解圆锥的母线长是扇形的半径,圆锥的底面圆周长是扇形的弧长.
3.已知圆锥的母线长为6cm,底面圆的半径为3cm,则此圆锥侧面展开图的圆心角是( )
A.
30°
B.60°
C.90°
D.
180°
考点:
圆锥的计算.
分析:
根据弧长=圆锥底面周长=6π,圆心角=弧长×180÷母线长÷π计算.
解答:
解:由题意知:弧长=圆锥底面周长=2×3π=6πcm,
扇形的圆心角=弧长×180÷母线长÷π=6π×180÷6π=180°.
故选:D.
点评:
本题考查的知识点为:弧长=圆锥底面周长及弧长与圆心角的关系.解题的关键是熟知圆锥与扇形的相关元素的对应关系.
4.一个圆锥的侧面展开图是半径为6的半圆,则这个圆锥的底面半径为( )
A.
1.5
B.2
C.2.5
D.
3
考点:
圆锥的计算.
专题:
计算题.
分析:
半径为6的半圆的弧长是6π,圆锥的底面周长等于侧面展开图的扇形弧长,因而圆锥的底面周长是6π,然后利用弧长公式计算.
解答:
解:设圆锥的底面半径是r,半径为6的半圆的弧长是6π,
则得到2πr=6π,
解得:r=3,
这个圆锥的底面半径是3.
故选:D.
点评:
本题综合考查有关扇形和圆锥的相关计算.解题思路:解决此类问题时要紧紧抓住两者之间的两个对应关系:(1)圆锥的母线长等于侧面展开图的扇形半径;(2)圆锥的底面周长等于侧面展开图的扇形弧长.
正确对这两个关系的记忆是解题的关键.
5.如果圆锥的母线长为5cm,底面半径为2cm,那么这个圆锥的侧面积为( )
A.
10cm2
B.10πcm2
C.20cm2
D.
20πcm2
考点:
圆锥的计算.
专题:
数形结合.
分析:
圆锥的侧面积=底面周长×母线长÷2.
解答:
解:圆锥的侧面积=2π×2×5÷2=10π.
故选:B.
点评:
本题考查了圆锥的计算,解题的关键是知道圆锥的侧面积的计算方法.
6.一个圆锥的底面半径是6cm,其侧面展开图为半圆,则圆锥的母线长为( )
A.
9cm
B.12cm
C.15cm
D.
18cm
考点:
圆锥的计算.
专题:
计算题.
分析:
圆锥的母线长=圆锥的底面周长×.
解答:
解:圆锥的母线长=2×π×6×=12cm,
故选:B.
点评:
本题考查圆锥的母线长的求法,注意利用圆锥的弧长等于底面周长这个知识点.
7.如图,某同学用一扇形纸板为一个玩偶制作一个圆锥形帽子,已知扇形半径OA=13cm,扇形的弧长为10πcm,那么这个圆锥形帽子的高是( )cm.(不考虑接缝)
A.
5
B.12
C.13
D.
14
考点:
圆锥的计算.
专题:
几何图形问题.
分析:
首先求得圆锥的底面半径,然后利用勾股定理求得圆锥的高即可.
解答:
解:先求底面圆的半径,即2πr=10π,r=5cm,
∵扇形的半径13cm,
∴圆锥的高==12cm.
故选:B.
点评:
此题主要考查圆锥的侧面展开图和勾股定理的应用,牢记有关公式是解答本题的关键,难度不大.
8.如图是一个几何体的三视图,则这个几何体的侧面积是( )
A.
πcm2
B.2πcm2
C.6πcm2
D.
3πcm2
考点:
圆锥的计算;由三视图判断几何体.
专题:
常规题型.
分析:
俯视图为圆的只有圆锥,圆柱,球,根据主视图和左视图都是三角形可得到此几何体为圆锥,那么侧面积=底面周长×母线长÷2.
解答:
解:此几何体为圆锥;
∵半径为1cm,高为3cm,
∴圆锥母线长为cm,
∴侧面积=2πrR÷2=πcm2;
故选:A.
点评:
本题考查了圆锥的计算,该三视图中的数据确定圆锥的底面直径和高是解本题的关键;本题体现了数形结合的数学思想,注意圆锥的高,母线长,底面半径组成直角三角形.
二.填空题(共6小题)
9.圆锥的底面半径为6cm,母线长为10cm,则圆锥的侧面积为 60π cm2.
考点:
圆锥的计算.
专题:
计算题.
分析:
圆锥的侧面积=π×底面半径×母线长,把相应数值代入即可求解.
解答:
解:圆锥的侧面积=π×6×10=60πcm2.
点评:
本题考查圆锥侧面积公式的运用,掌握公式是关键.
10.一个底面直径是80cm,母线长为90cm的圆锥的侧面展开图的圆心角的度数为 160° .
考点:
圆锥的计算.
专题:
计算题.
分析:
根据圆锥的底面直径求得圆锥的侧面展开扇形的弧长,再利用告诉的母线长求得圆锥的侧面展开扇形的面积,再利用扇形的另一种面积的计算方法求得圆锥的侧面展开图的圆心角即可.
解答:
解:∵圆锥的底面直径是80cm,
∴圆锥的侧面展开扇形的弧长为:πd=80π,
∵母线长90cm,
∴圆锥的侧面展开扇形的面积为:lr=×80π×90=3600π,
∴=3600π,
解得:n=160.
故答案为:160.
点评:
本题考查了圆锥的有关计算,解决此类题目的关键是明确圆锥的侧面展开扇形与圆锥的关系.
11.有一圆锥,它的高为8cm,底面半径为6cm,则这个圆锥的侧面积是 60π cm2.(结果保留π)
考点:
圆锥的计算.
分析:
先根据圆锥的底面半径和高求出母线长,圆锥的侧面积是展开后扇形的面积,计算可得.
解答:
解:圆锥的母线==10cm,
圆锥的底面周长2πr=12πcm,
圆锥的侧面积=lR=×12π×10=60πcm2.
故答案为:60π.
点评:
本题考查了圆锥的计算,圆锥的高和圆锥的底面半径圆锥的母线组成直角三角形,扇形的面积公式为lR.
12.圆锥的底面半径是2cm,母线长6cm,则这个圆锥侧面展开图的扇形圆心角度数为 120 度.
考点:
圆锥的计算.
专题:
计算题.
分析:
根据展开图的扇形的弧长等于圆锥底面周长计算.
解答:
解:∵圆锥的底面半径是2cm,
∴圆锥的底面周长为4π,
设圆心角为n°,根据题意得:=4π,
解得n=120.
故答案为:120.
点评:
考查了圆锥的计算,圆锥的侧面展开图是一个扇形,此扇形的弧长等于圆锥底面周长,扇形的半径等于圆锥的母线长.本题就是把的扇形的弧长等于圆锥底面周长作为相等关系,列方程求解.
13.用一个圆心角为240°半径为6的扇形做一个圆锥的侧面,则这个圆锥底面半径为 4 .
考点:
圆锥的计算.
专题:
计算题.
分析:
易得扇形的弧长,除以2π即为圆锥的底面半径.
解答:
解:∵扇形的弧长==8π,
∴圆锥的底面半径为8π÷2π=4.
故答案为:4.
点评:
考查了扇形的弧长公式;圆的周长公式;用到的知识点为:圆锥的弧长等于底面周长.
14.一个底面直径为10cm,母线长为15cm的圆锥,它的侧面展开图圆心角是 120 度.
考点:
圆锥的计算.
专题:
计算题.
分析:
利用底面周长=展开图的弧长可得.
解答:
解:∵底面直径为10cm,
∴底面周长为10π,
根据题意得10π=,
解得n=120.
故答案为:120.
点评:
考查了圆锥的计算,解答本题的关键是有确定底面周长=展开图的弧长这个等量关系,然后由扇形的弧长公式和圆的周长公式求值.
三.解答题(共8小题)
15.如图是某圆锥的三视图,请根据图中尺寸计算该圆锥的全面积.(结果保留3个有效数字)
考点:
圆锥的计算;由三视图判断几何体.
分析:
首先根据三视图确定圆锥的高和底面半径,然后求得母线长,然后代入圆锥表面积=底面积+侧面积=π×底面半径2+π×底面半径×母线长,把相应数值代入即可求解.
解答:
解:由三视图知:圆锥的高为2cm,底面半径为2cm,
∴圆锥的母线长为4,
∴圆锥表面积=π×22+π×2×4=12π≈37.7.
点评:
本题考查圆锥全面积公式的运用,掌握公式是关键.
16.如图,圆锥的侧面展开图是一个半圆,求母线AB与高AO的夹角.参考公式:圆锥的侧面积S=πrl,其中r为底面半径,l为母线长.
考点:
圆锥的计算.
分析:
设出圆锥的半径与母线长,利用圆锥的底面周长等于侧面展开图的弧长得到圆锥的半径与母线长,进而表示出母线与高的夹角的正弦值,也就求出了夹角的度数.
解答:
解:设圆锥的母线长为l,底面半径为r,
则:πl=2πr,
∴l=2r,
∴母线与高的夹角的正弦值==,
∴母线AB与高AO的夹角30°.
点评:
此题主要考查了圆锥的侧面展开图的弧长等于圆锥的底面周长;注意利用一个角相应的三角函数值求得角的度数.
17.已知圆锥的侧面积为16πcm2.
(1)求圆锥的母线长L(cm)关于底面半径r(cm)之间的函数关系式;
(2)写出自变量r的取值范围;
(3)当圆锥的侧面展开图是圆心角为90°的扇形时,求圆锥的高.
考点:
圆锥的计算;反比例函数的应用.
专题:
计算题.
分析:
(1)根据圆锥的底面周长等于圆锥侧面展开扇形的弧长,用圆锥的底面半径和母线长表示出其侧面积就能得到;
(2)根据底面半径小于其母线长且大于零确定底面半径的取值范围;
(3)根据圆锥的侧面积和其圆心角的度数求出其母线长,然后利用勾股定理求圆锥的高.
解答:
解:(1)∵S=πrL=16πcm2,
∴L=cm;
(2)∵L=>r>0,
∴0<r<4;
(3)∵θ=90°=×360°,
∴L=4r,
又L=,
∴r=2cm,
∴L=8cm,
∴h=2cm.
点评:
本题考查了圆锥的侧面积与圆锥的底面积之间的相互转化,二者通过圆锥的母线、圆锥的底面周长与圆锥的侧面展开扇形的弧长建立关系.
18.如图:扇形OAB的圆心角∠AOB=120°,半径OA=6cm,
(1)请你用尺规作图的方法作出扇形的对称轴(不写作法,保留作图痕迹)
(2)若将此扇形围成一个圆锥的侧面,求圆锥底面圆的半径.
考点:
圆锥的计算;作图—复杂作图.
分析:
(1)连接AB,作弦AB的垂直平分线即可作出扇形的对称轴,
(2)利用圆锥的底面周长等于侧面展开图的扇形弧长是4π,列出方程计算.
解答:
解:(1)如图所示:
(2)扇形的圆心角是120°,半径为6cm,
则扇形的弧长是:==4π
则圆锥的底面周长等于侧面展开图的扇形弧长是4π,
设圆锥的底面半径是r,
则2πr=4π,
解得:r=2.
圆锥的底面半径是2cm.
点评:
本题综合考查有关扇形和圆锥的相关计算.解题思路:解决此类问题时要紧紧抓住两者之间的两个对应关系:
(1)圆锥的母线长等于侧面展开图的扇形半径;
(2)圆锥的底面周长等于侧面展开图的扇形弧长.正确对这两个关系的记忆是解题的关键.
19.在△ABC中,∠C=90°,∠A=30°,BC=3.
(1)将△ABC绕AB所在的直线旋转一周,求所得几何体的侧面积;
(2)折叠△ABC,使BC边与CA边重合,求折痕长和重叠部分的面积.
考点:
圆锥的计算;点、线、面、体;翻折变换(折叠问题).
分析:
(1)易得所得几何体的侧面积为2个底面半径为CH,母线长为AC,BC的圆锥,那么侧面积=π×母线长×底面半径求出即可得出;
(2)首先求出BE的长,进而求出CE,DE,即可得出面积.
解答:
解:(1)∵∠C=90°,∠A=30°,BC=3,
∴tan30°==,AB=6,
∴AC=,
∵CH×AB=BC×AC,
∴3×3=6×CH,
∴CH=R=,
;
(2)过点E作ED⊥AC于点D,设折叠后点B落在点G,折痕是CE,则CG=BC=3,
∴BE=EG=GA=3﹣3,
∴AE=6﹣BE=9﹣3;
∴DE=,
∴CE=,
S△BCE= BE CH=,(或S△CGE=).
点评:
此题主要考查了图形翻折变换以及圆锥的有关计算,根据已知得出旋转后的图形以及熟练利用翻折变换的性质得出是解题关键.
20如图,圆锥底面的半径为10cm,高为10cm.
(1)求圆锥的全面积;
(2)若一只蚂蚁从底面上一点A出发绕圆锥一周回到SA上一点M处,且SM=3AM,求它所走的最短距离.
考点:
圆锥的计算;平面展开-最短路径问题.
专题:
计算题.
分析:
(1)首先求得圆锥的母线长,然后求得展开扇形的弧长,进而求得其侧面积和底面积,从而求得其全面积;
(2)将圆锥的侧面展开,求得其展开扇形的圆心角的度数是90°,利用勾股定理求得AM的长即为最短距离.
解答:
解:(1)由题意,可得圆锥的母线SA==40(cm)
圆锥的侧面展开扇形的弧长l=2π OA=20πcm
∴S侧=L SA=400πcm2
S圆=πAO2=100πcm2,
∴S全=S圆+S底=(400+100)π=500π(cm2);
(2)沿母线SA将圆锥的侧面展开,如右图,则线段AM的长就是蚂蚁所走的最短距离
由(1)知,SA=40cm,弧AA′=20πcm
∵=20πcm,
∴∠S=n==90°,
∵SA′=SA=40cm,SM=3A′M
∴SM=30cm,
∴在Rt△ASM中,由勾股定理得AM=50(cm)
所以,蚂蚁所走的最短距离是50cm.
点评:
本题利用了勾股定理,弧长公式,圆的周长公式,等直角三角形的性质求解.
21.如图,现有一圆心角为90°,半径为8cm的扇形纸片,用它恰好围成一个圆锥的侧面(接缝忽略不计),求该圆锥底面圆的面积.(结果保留π)
考点:
圆锥的计算.
分析:
本题的关键是利用弧长公式计算弧长,再利用底面周长=展开图的弧长可得.
解答:
解:设圆锥的底面半径为R,则L==2πR,
解R=2cm,
∴该圆锥底面圆的面积为4πcm2.
点评:
本题考查了圆锥的计算,解答本题的关键是有确定底面周长=展开图的弧长这个等量关系,然后由扇形的弧长公式和圆的周长公式求值.
22.如图,一个圆锥的高为cm,侧面展开图是半圆.求:
(1)圆锥的母线长与底面半径之比;
(2)求∠BAC的度数;
(3)圆锥的侧面积(结果保留π).
考点:
圆锥的计算;弧长的计算.
分析:
(1)直接根据圆锥的侧面展开图扇形的弧长等于圆锥底面周长可得比值;
(2)利用圆锥的高,母线和底面半径构造的直角三角形中的勾股定理和等腰三角形的基本性质解题即可;
(3)圆锥的侧面积是展开图扇形的面积,直接利用公式解题即可,圆锥的侧面积为.
解答:
解:(1)设此圆锥的高为h,底面半径为r,母线长AC=l,
∵2πr=πl,
∴l:r=2:1;
(2)∵AO⊥OC,=2,
∴圆锥高与母线的夹角为30°,
则∠BAC=60°;
(3)由图可知l2=h2+r2,h=3cm,
∴(2r)2=(3)2+r2,即4r2=27+r2,
解得r=3cm,
∴l=2r=6cm,
∴圆锥的侧面积为=18π(cm2).
点评:
本题主要考查圆锥的特点和圆锥侧面面积的计算.
易错易混点:学生由于空间想象能力不够,找不到圆锥的底面半径,或者对圆锥的侧面面积公式运用不熟练,从而造成错误.
一.选择题(共8小题)
1.已知圆锥的底面半径为2cm,母线长为5cm,则圆锥的侧面积是( )
A.10cm2
B.5π
cm2
C.10π
cm2
D.20π
cm2
2.已知圆锥的高为4,母线长为5,则该圆锥的表面积为( )
A.21π
B.15π
C.12π
D.24π
3.已知圆锥的母线长为6cm,底面圆的半径为3cm,则此圆锥侧面展开图的圆心角是( )
A.30°
B.60°
C.90°
D.180°
4.一个圆锥的侧面展开图是半径为6的半圆,则这个圆锥的底面半径为( )
A.1.5
B.2
C.2.5
D.3
5.如果圆锥的母线长为5cm,底面半径为2cm,那么这个圆锥的侧面积为( )
A.10cm2
B.10πcm2
C.20cm2
D.20πcm2
6.一个圆锥的底面半径是6cm,其侧面展开图为半圆,则圆锥的母线长为( )
A.9cm
B.12cm
C.15cm
D.18cm
7.如图,某同学用一扇形纸板为一个玩偶制作一个圆锥形帽子,已知扇形半径OA=13cm,扇形的弧长为10πcm,那么这个圆锥形帽子的高是( )cm.(不考虑接缝)
A.5
B.12
C.13
D.14
8.如图是一个几何体的三视图,则这个几何体的侧面积是( )
A.πcm2
B.2πcm2
C.6πcm2
D.3πcm2
二.填空题(共6小题)
9.圆锥的底面半径为6cm,母线长为10cm,则圆锥的侧面积为 _________ cm2.
10.一个底面直径是80cm,母线长为90cm的圆锥的侧面展开图的圆心角的度数为 _________ .
11.有一圆锥,它的高为8cm,底面半径为6cm,则这个圆锥的侧面积是 _________ cm2.(结果保留π)
12.圆锥的底面半径是2cm,母线长6cm,则这个圆锥侧面展开图的扇形圆心角度数为 _________ 度.
13.用一个圆心角为240°半径为6的扇形做一个圆锥的侧面,则这个圆锥底面半径为 _________ .
14.一个底面直径为10cm,母线长为15cm的圆锥,它的侧面展开图圆心角是 _________ 度.
三.解答题(共8小题)
15.如图是某圆锥的三视图,请根据图中尺寸计算该圆锥的全面积.(结果保留3个有效数字)
16.如图,圆锥的侧面展开图是一个半圆,求母线AB与高AO的夹角.参考公式:圆锥的侧面积S=πrl,其中r为底面半径,l为母线长.
17.已知圆锥的侧面积为16πcm2.
(1)求圆锥的母线长L(cm)关于底面半径r(cm)之间的函数关系式;
(2)写出自变量r的取值范围;
(3)当圆锥的侧面展开图是圆心角为90°的扇形时,求圆锥的高.
18.如图:扇形OAB的圆心角∠AOB=120°,半径OA=6cm,
(1)请你用尺规作图的方法作出扇形的对称轴(不写作法,保留作图痕迹)
(2)若将此扇形围成一个圆锥的侧面,求圆锥底面圆的半径.
19.在△ABC中,∠C=90°,∠A=30°,BC=3.
(1)将△ABC绕AB所在的直线旋转一周,求所得几何体的侧面积;
(2)折叠△ABC,使BC边与CA边重合,求折痕长和重叠部分的面积.
20.如图,圆锥底面的半径为10cm,高为10cm.
(1)求圆锥的全面积;
(2)若一只蚂蚁从底面上一点A出发绕圆锥一周回到SA上一点M处,且SM=3AM,求它所走的最短距离.
21.如图,现有一圆心角为90°,半径为8cm的扇形纸片,用它恰好围成一个圆锥的侧面(接缝忽略不计),求该圆锥底面圆的面积.(结果保留π)
22.如图,一个圆锥的高为cm,侧面展开图是半圆.求:
(1)圆锥的母线长与底面半径之比;
(2)求∠BAC的度数;
(3)圆锥的侧面积(结果保留π).
27.3.2圆锥的侧面积和全面积
参考答案与试题解析
一.选择题(共8小题)
1.已知圆锥的底面半径为2cm,母线长为5cm,则圆锥的侧面积是( )
A.
10cm2
B.5π
cm2
C.10π
cm2
D.
20π
cm2
考点:
圆锥的计算.
专题:
计算题.
分析:
根据圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和扇形的面积公式计算即可.
解答:
解:圆锥的侧面积= 2π 2 5=10π(cm2).
故选C.
点评:
本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.
2.已知圆锥的高为4,母线长为5,则该圆锥的表面积为( )
A.
21π
B.15π
C.12π
D.
24π
考点:
圆锥的计算.版权所有
分析:
首先根据勾股定理求得底面半径,则可以得到底面周长,然后利用扇形的面积公式即可求解.
解答:
解:底面半径是:=3,则底面周长是6π,
则圆锥的侧面积是:×6π×5=15π,底面积为9π,
则表面积为15π+9π=24π.
故选D.
点评:
考查了圆锥的计算.正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键,理解圆锥的母线长是扇形的半径,圆锥的底面圆周长是扇形的弧长.
3.已知圆锥的母线长为6cm,底面圆的半径为3cm,则此圆锥侧面展开图的圆心角是( )
A.
30°
B.60°
C.90°
D.
180°
考点:
圆锥的计算.
分析:
根据弧长=圆锥底面周长=6π,圆心角=弧长×180÷母线长÷π计算.
解答:
解:由题意知:弧长=圆锥底面周长=2×3π=6πcm,
扇形的圆心角=弧长×180÷母线长÷π=6π×180÷6π=180°.
故选:D.
点评:
本题考查的知识点为:弧长=圆锥底面周长及弧长与圆心角的关系.解题的关键是熟知圆锥与扇形的相关元素的对应关系.
4.一个圆锥的侧面展开图是半径为6的半圆,则这个圆锥的底面半径为( )
A.
1.5
B.2
C.2.5
D.
3
考点:
圆锥的计算.
专题:
计算题.
分析:
半径为6的半圆的弧长是6π,圆锥的底面周长等于侧面展开图的扇形弧长,因而圆锥的底面周长是6π,然后利用弧长公式计算.
解答:
解:设圆锥的底面半径是r,半径为6的半圆的弧长是6π,
则得到2πr=6π,
解得:r=3,
这个圆锥的底面半径是3.
故选:D.
点评:
本题综合考查有关扇形和圆锥的相关计算.解题思路:解决此类问题时要紧紧抓住两者之间的两个对应关系:(1)圆锥的母线长等于侧面展开图的扇形半径;(2)圆锥的底面周长等于侧面展开图的扇形弧长.
正确对这两个关系的记忆是解题的关键.
5.如果圆锥的母线长为5cm,底面半径为2cm,那么这个圆锥的侧面积为( )
A.
10cm2
B.10πcm2
C.20cm2
D.
20πcm2
考点:
圆锥的计算.
专题:
数形结合.
分析:
圆锥的侧面积=底面周长×母线长÷2.
解答:
解:圆锥的侧面积=2π×2×5÷2=10π.
故选:B.
点评:
本题考查了圆锥的计算,解题的关键是知道圆锥的侧面积的计算方法.
6.一个圆锥的底面半径是6cm,其侧面展开图为半圆,则圆锥的母线长为( )
A.
9cm
B.12cm
C.15cm
D.
18cm
考点:
圆锥的计算.
专题:
计算题.
分析:
圆锥的母线长=圆锥的底面周长×.
解答:
解:圆锥的母线长=2×π×6×=12cm,
故选:B.
点评:
本题考查圆锥的母线长的求法,注意利用圆锥的弧长等于底面周长这个知识点.
7.如图,某同学用一扇形纸板为一个玩偶制作一个圆锥形帽子,已知扇形半径OA=13cm,扇形的弧长为10πcm,那么这个圆锥形帽子的高是( )cm.(不考虑接缝)
A.
5
B.12
C.13
D.
14
考点:
圆锥的计算.
专题:
几何图形问题.
分析:
首先求得圆锥的底面半径,然后利用勾股定理求得圆锥的高即可.
解答:
解:先求底面圆的半径,即2πr=10π,r=5cm,
∵扇形的半径13cm,
∴圆锥的高==12cm.
故选:B.
点评:
此题主要考查圆锥的侧面展开图和勾股定理的应用,牢记有关公式是解答本题的关键,难度不大.
8.如图是一个几何体的三视图,则这个几何体的侧面积是( )
A.
πcm2
B.2πcm2
C.6πcm2
D.
3πcm2
考点:
圆锥的计算;由三视图判断几何体.
专题:
常规题型.
分析:
俯视图为圆的只有圆锥,圆柱,球,根据主视图和左视图都是三角形可得到此几何体为圆锥,那么侧面积=底面周长×母线长÷2.
解答:
解:此几何体为圆锥;
∵半径为1cm,高为3cm,
∴圆锥母线长为cm,
∴侧面积=2πrR÷2=πcm2;
故选:A.
点评:
本题考查了圆锥的计算,该三视图中的数据确定圆锥的底面直径和高是解本题的关键;本题体现了数形结合的数学思想,注意圆锥的高,母线长,底面半径组成直角三角形.
二.填空题(共6小题)
9.圆锥的底面半径为6cm,母线长为10cm,则圆锥的侧面积为 60π cm2.
考点:
圆锥的计算.
专题:
计算题.
分析:
圆锥的侧面积=π×底面半径×母线长,把相应数值代入即可求解.
解答:
解:圆锥的侧面积=π×6×10=60πcm2.
点评:
本题考查圆锥侧面积公式的运用,掌握公式是关键.
10.一个底面直径是80cm,母线长为90cm的圆锥的侧面展开图的圆心角的度数为 160° .
考点:
圆锥的计算.
专题:
计算题.
分析:
根据圆锥的底面直径求得圆锥的侧面展开扇形的弧长,再利用告诉的母线长求得圆锥的侧面展开扇形的面积,再利用扇形的另一种面积的计算方法求得圆锥的侧面展开图的圆心角即可.
解答:
解:∵圆锥的底面直径是80cm,
∴圆锥的侧面展开扇形的弧长为:πd=80π,
∵母线长90cm,
∴圆锥的侧面展开扇形的面积为:lr=×80π×90=3600π,
∴=3600π,
解得:n=160.
故答案为:160.
点评:
本题考查了圆锥的有关计算,解决此类题目的关键是明确圆锥的侧面展开扇形与圆锥的关系.
11.有一圆锥,它的高为8cm,底面半径为6cm,则这个圆锥的侧面积是 60π cm2.(结果保留π)
考点:
圆锥的计算.
分析:
先根据圆锥的底面半径和高求出母线长,圆锥的侧面积是展开后扇形的面积,计算可得.
解答:
解:圆锥的母线==10cm,
圆锥的底面周长2πr=12πcm,
圆锥的侧面积=lR=×12π×10=60πcm2.
故答案为:60π.
点评:
本题考查了圆锥的计算,圆锥的高和圆锥的底面半径圆锥的母线组成直角三角形,扇形的面积公式为lR.
12.圆锥的底面半径是2cm,母线长6cm,则这个圆锥侧面展开图的扇形圆心角度数为 120 度.
考点:
圆锥的计算.
专题:
计算题.
分析:
根据展开图的扇形的弧长等于圆锥底面周长计算.
解答:
解:∵圆锥的底面半径是2cm,
∴圆锥的底面周长为4π,
设圆心角为n°,根据题意得:=4π,
解得n=120.
故答案为:120.
点评:
考查了圆锥的计算,圆锥的侧面展开图是一个扇形,此扇形的弧长等于圆锥底面周长,扇形的半径等于圆锥的母线长.本题就是把的扇形的弧长等于圆锥底面周长作为相等关系,列方程求解.
13.用一个圆心角为240°半径为6的扇形做一个圆锥的侧面,则这个圆锥底面半径为 4 .
考点:
圆锥的计算.
专题:
计算题.
分析:
易得扇形的弧长,除以2π即为圆锥的底面半径.
解答:
解:∵扇形的弧长==8π,
∴圆锥的底面半径为8π÷2π=4.
故答案为:4.
点评:
考查了扇形的弧长公式;圆的周长公式;用到的知识点为:圆锥的弧长等于底面周长.
14.一个底面直径为10cm,母线长为15cm的圆锥,它的侧面展开图圆心角是 120 度.
考点:
圆锥的计算.
专题:
计算题.
分析:
利用底面周长=展开图的弧长可得.
解答:
解:∵底面直径为10cm,
∴底面周长为10π,
根据题意得10π=,
解得n=120.
故答案为:120.
点评:
考查了圆锥的计算,解答本题的关键是有确定底面周长=展开图的弧长这个等量关系,然后由扇形的弧长公式和圆的周长公式求值.
三.解答题(共8小题)
15.如图是某圆锥的三视图,请根据图中尺寸计算该圆锥的全面积.(结果保留3个有效数字)
考点:
圆锥的计算;由三视图判断几何体.
分析:
首先根据三视图确定圆锥的高和底面半径,然后求得母线长,然后代入圆锥表面积=底面积+侧面积=π×底面半径2+π×底面半径×母线长,把相应数值代入即可求解.
解答:
解:由三视图知:圆锥的高为2cm,底面半径为2cm,
∴圆锥的母线长为4,
∴圆锥表面积=π×22+π×2×4=12π≈37.7.
点评:
本题考查圆锥全面积公式的运用,掌握公式是关键.
16.如图,圆锥的侧面展开图是一个半圆,求母线AB与高AO的夹角.参考公式:圆锥的侧面积S=πrl,其中r为底面半径,l为母线长.
考点:
圆锥的计算.
分析:
设出圆锥的半径与母线长,利用圆锥的底面周长等于侧面展开图的弧长得到圆锥的半径与母线长,进而表示出母线与高的夹角的正弦值,也就求出了夹角的度数.
解答:
解:设圆锥的母线长为l,底面半径为r,
则:πl=2πr,
∴l=2r,
∴母线与高的夹角的正弦值==,
∴母线AB与高AO的夹角30°.
点评:
此题主要考查了圆锥的侧面展开图的弧长等于圆锥的底面周长;注意利用一个角相应的三角函数值求得角的度数.
17.已知圆锥的侧面积为16πcm2.
(1)求圆锥的母线长L(cm)关于底面半径r(cm)之间的函数关系式;
(2)写出自变量r的取值范围;
(3)当圆锥的侧面展开图是圆心角为90°的扇形时,求圆锥的高.
考点:
圆锥的计算;反比例函数的应用.
专题:
计算题.
分析:
(1)根据圆锥的底面周长等于圆锥侧面展开扇形的弧长,用圆锥的底面半径和母线长表示出其侧面积就能得到;
(2)根据底面半径小于其母线长且大于零确定底面半径的取值范围;
(3)根据圆锥的侧面积和其圆心角的度数求出其母线长,然后利用勾股定理求圆锥的高.
解答:
解:(1)∵S=πrL=16πcm2,
∴L=cm;
(2)∵L=>r>0,
∴0<r<4;
(3)∵θ=90°=×360°,
∴L=4r,
又L=,
∴r=2cm,
∴L=8cm,
∴h=2cm.
点评:
本题考查了圆锥的侧面积与圆锥的底面积之间的相互转化,二者通过圆锥的母线、圆锥的底面周长与圆锥的侧面展开扇形的弧长建立关系.
18.如图:扇形OAB的圆心角∠AOB=120°,半径OA=6cm,
(1)请你用尺规作图的方法作出扇形的对称轴(不写作法,保留作图痕迹)
(2)若将此扇形围成一个圆锥的侧面,求圆锥底面圆的半径.
考点:
圆锥的计算;作图—复杂作图.
分析:
(1)连接AB,作弦AB的垂直平分线即可作出扇形的对称轴,
(2)利用圆锥的底面周长等于侧面展开图的扇形弧长是4π,列出方程计算.
解答:
解:(1)如图所示:
(2)扇形的圆心角是120°,半径为6cm,
则扇形的弧长是:==4π
则圆锥的底面周长等于侧面展开图的扇形弧长是4π,
设圆锥的底面半径是r,
则2πr=4π,
解得:r=2.
圆锥的底面半径是2cm.
点评:
本题综合考查有关扇形和圆锥的相关计算.解题思路:解决此类问题时要紧紧抓住两者之间的两个对应关系:
(1)圆锥的母线长等于侧面展开图的扇形半径;
(2)圆锥的底面周长等于侧面展开图的扇形弧长.正确对这两个关系的记忆是解题的关键.
19.在△ABC中,∠C=90°,∠A=30°,BC=3.
(1)将△ABC绕AB所在的直线旋转一周,求所得几何体的侧面积;
(2)折叠△ABC,使BC边与CA边重合,求折痕长和重叠部分的面积.
考点:
圆锥的计算;点、线、面、体;翻折变换(折叠问题).
分析:
(1)易得所得几何体的侧面积为2个底面半径为CH,母线长为AC,BC的圆锥,那么侧面积=π×母线长×底面半径求出即可得出;
(2)首先求出BE的长,进而求出CE,DE,即可得出面积.
解答:
解:(1)∵∠C=90°,∠A=30°,BC=3,
∴tan30°==,AB=6,
∴AC=,
∵CH×AB=BC×AC,
∴3×3=6×CH,
∴CH=R=,
;
(2)过点E作ED⊥AC于点D,设折叠后点B落在点G,折痕是CE,则CG=BC=3,
∴BE=EG=GA=3﹣3,
∴AE=6﹣BE=9﹣3;
∴DE=,
∴CE=,
S△BCE= BE CH=,(或S△CGE=).
点评:
此题主要考查了图形翻折变换以及圆锥的有关计算,根据已知得出旋转后的图形以及熟练利用翻折变换的性质得出是解题关键.
20如图,圆锥底面的半径为10cm,高为10cm.
(1)求圆锥的全面积;
(2)若一只蚂蚁从底面上一点A出发绕圆锥一周回到SA上一点M处,且SM=3AM,求它所走的最短距离.
考点:
圆锥的计算;平面展开-最短路径问题.
专题:
计算题.
分析:
(1)首先求得圆锥的母线长,然后求得展开扇形的弧长,进而求得其侧面积和底面积,从而求得其全面积;
(2)将圆锥的侧面展开,求得其展开扇形的圆心角的度数是90°,利用勾股定理求得AM的长即为最短距离.
解答:
解:(1)由题意,可得圆锥的母线SA==40(cm)
圆锥的侧面展开扇形的弧长l=2π OA=20πcm
∴S侧=L SA=400πcm2
S圆=πAO2=100πcm2,
∴S全=S圆+S底=(400+100)π=500π(cm2);
(2)沿母线SA将圆锥的侧面展开,如右图,则线段AM的长就是蚂蚁所走的最短距离
由(1)知,SA=40cm,弧AA′=20πcm
∵=20πcm,
∴∠S=n==90°,
∵SA′=SA=40cm,SM=3A′M
∴SM=30cm,
∴在Rt△ASM中,由勾股定理得AM=50(cm)
所以,蚂蚁所走的最短距离是50cm.
点评:
本题利用了勾股定理,弧长公式,圆的周长公式,等直角三角形的性质求解.
21.如图,现有一圆心角为90°,半径为8cm的扇形纸片,用它恰好围成一个圆锥的侧面(接缝忽略不计),求该圆锥底面圆的面积.(结果保留π)
考点:
圆锥的计算.
分析:
本题的关键是利用弧长公式计算弧长,再利用底面周长=展开图的弧长可得.
解答:
解:设圆锥的底面半径为R,则L==2πR,
解R=2cm,
∴该圆锥底面圆的面积为4πcm2.
点评:
本题考查了圆锥的计算,解答本题的关键是有确定底面周长=展开图的弧长这个等量关系,然后由扇形的弧长公式和圆的周长公式求值.
22.如图,一个圆锥的高为cm,侧面展开图是半圆.求:
(1)圆锥的母线长与底面半径之比;
(2)求∠BAC的度数;
(3)圆锥的侧面积(结果保留π).
考点:
圆锥的计算;弧长的计算.
分析:
(1)直接根据圆锥的侧面展开图扇形的弧长等于圆锥底面周长可得比值;
(2)利用圆锥的高,母线和底面半径构造的直角三角形中的勾股定理和等腰三角形的基本性质解题即可;
(3)圆锥的侧面积是展开图扇形的面积,直接利用公式解题即可,圆锥的侧面积为.
解答:
解:(1)设此圆锥的高为h,底面半径为r,母线长AC=l,
∵2πr=πl,
∴l:r=2:1;
(2)∵AO⊥OC,=2,
∴圆锥高与母线的夹角为30°,
则∠BAC=60°;
(3)由图可知l2=h2+r2,h=3cm,
∴(2r)2=(3)2+r2,即4r2=27+r2,
解得r=3cm,
∴l=2r=6cm,
∴圆锥的侧面积为=18π(cm2).
点评:
本题主要考查圆锥的特点和圆锥侧面面积的计算.
易错易混点:学生由于空间想象能力不够,找不到圆锥的底面半径,或者对圆锥的侧面面积公式运用不熟练,从而造成错误.
