18.5 相似三角形的判定 同步练习(含答案)
文档属性
| 名称 | 18.5 相似三角形的判定 同步练习(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 246.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-11-07 16:05:47 | ||
图片预览



文档简介
18.5
相似三角形的判定
基础能力训练
◆相似三角形的判定
1.已知菱形ABCD的边长是6,点E在直线AD上,DE=3,联结BE与对角线AC相交于点M,则的值是______.
2.如图19-5-4所示,E是平行四边形ABCD的一边BA延长线上的一点,CE交AD于点F,图中共有______对相似三角形,按对应顶点写出图中的相似三角形____________________.
3.如图19-5-5所示,已知△ABC中,AB=AC,∠A=36°,BD平分∠ABC,则BD=_______=_______.
4.如图19-5-6所示,∠l=∠2,若再增加一个条件就能使结论“AB·DE=AD·BC”成立,则这个条件可以是_______.
5.如图19-5-7所示,△ACD和△ABC具备下列哪个条件时,它们相似(
)
A.
B.
C.CB2=AD·BD
D.AC2=AD·AB
6.用—个放大镜看一个直角三角形,该直角三角形的边长放大到原来的5倍后,下列结论正确的是(
)
A.每个内角是原来的5倍
B.周长是原来的5倍
C.面积是原来的5倍
D.两条直角边的比值是原来的5倍
7.下列条件能判别△ABC~△DEF的是(
)
A.AB=4
cm,AC=3.2
cm,DE=2
cm,DF=1.6
cm,∠B=∠E=50°
B.AB=6
cm,BC=9
cm,AC=7.5
cm,DE=8
cm,EF=12
cm.DF=10
cm
C.∠A=∠D=70°,∠B=50°,∠E=60°
D.∠B=∠E=90°,
8.某班在布置新年联欢会会场时,需要将直角三角形彩纸裁成长度不等的矩形纸条,如图19-5-8所示,在Rt△ABC中,∠C=90°,AC=30
cm,AB=50
cm,依次裁下宽为1
cm的纸条a1、a2、a3、…,若使裁得的矩形纸条长度不小于5
cm,则每张直角三角形彩纸能裁成矩形纸条的条数为(
)
A.24
B.25
C.26
D.27
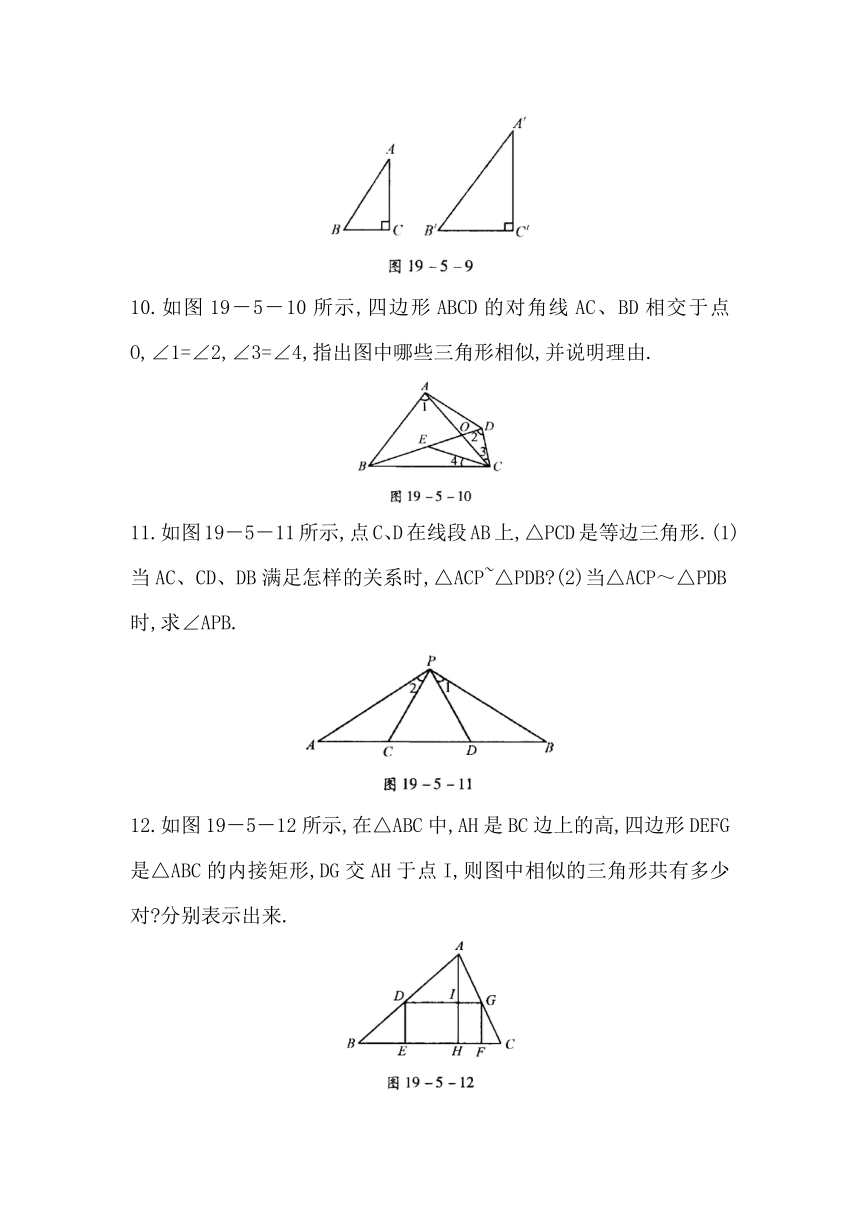
9.已知,如图19-5-9,Rt△∠ABC和Rt△A′B′C′中∠C=∠C′=90°,.△ABC与△A′B′C′是否相似,并说明理由.
10.如图19-5-10所示,四边形ABCD的对角线AC、BD相交于点O,∠1=∠2,∠3=∠4,指出图中哪些三角形相似,并说明理由.
11.如图19-5-11所示,点C、D在线段AB上,△PCD是等边三角形.(1)当AC、CD、DB满足怎样的关系时,△ACP~△PDB (2)当△ACP~△PDB时,求∠APB.
12.如图19-5-12所示,在△ABC中,AH是BC边上的高,四边形DEFG是△ABC的内接矩形,DG交AH于点I,则图中相似的三角形共有多少对 分别表示出来.
13.如果两个三角形中有两边和其中一边上的高对应成比例,则这两个三角形相似吗
综合创新训练
◆创新训练
14.已知:如图19-5-13,在平面直角坐标系中,矩形AOBC有两个顶点的坐标分别是A(0,6),C(8,6),x轴的正半轴上有一动点E(E与B不重合),作直线AE交对角线OC于D,或AE与BC相交于点F.
当点E在O、B间运动到某些位置时,作直线AE后,图中会出现相似不全等的三角形,请你把这个相似三角形写出来:_______;当E点运动到B点的右边时,请你写出此时图中三对相似而不全等的三角形:__________________.
15.如图19-5-14所示,在△ABC中,AB=8
am,BC=16
cm,点P从点A开始沿AB边向点B以2cm/s的速度移动,点Q从点B开始沿BC边向点C以4
cm/s的速度移动.如果P、Q分别从A、B同时出发,经过几秒钟△PBQ与原△ABC相似
16.一个圆柱形油桶,半径为1米,高为1.5米,用一根2米长的木棒从桶盖小口斜插桶内,另一端在小口处,抽出木棒后,量得上面没浸油的部分为1.2米,试求:
(1)油面的高度是多少
(2)桶内有油多少升 (1立方分米=1升,取3.14,取后结果精确到1升)
◆开放探索
17.如图19-5-15,在△ABC中,∠C=90°,P为AB上一点且点不与点A重合.过点P作PE⊥AB交AC边于E,点E不与点C重合.若AB=10,AC=8,设AP的长为x,四边形PECB的周长为y,试用x的代数式表示y.
参考答案
1答案:2或
解析:当点E在线段AD上时,如图(1),因为AB∥CD,所以△ABE~△DFE.所以,故DF=6.又因为△AMB~△CMF,所以.
当点E在线段AD的延长线上时,如图(2),容易得到△BCM~△EAM,
∴.
2答案:3
△EAF~△EBC,△EAF~△CDF,△EBC~△CDF
3答案:BC
AD
4答案:∠B=∠D,或∠C=∠AED,或AD:AB=AE:AC
解析:本题实质就是构造使△ADE与△ABC相似的条件.
5答案:D
解析:由AC2=AD·AB可得.又∠A=∠A,所以△ACD~△ABC.
6答案:B
7答案:B
解析:因为,三边对应成比例,所以两三角形相似.
8答案:C
解析:设第n条的长度恰好为5cm,且该矩形纸条与AC的交点为P点,与AB的交点为Q点,则PQ=5cm,设AP=x
cm,则△APQ~△ACB,得,即,解得:x=3.75,
∴CP=30-x=26.25.∵矩形宽为1
cm,取整数,可知矩形纸条为26条.
9答案:解析:相似,理由如下:∵,∴,两边平方,得,所以,由勾股定理得,因为,均为正数,则,即,而∠C=∠C′=90°,故Rt△ABC~Rt△A'B'C'.
10答案:解析:(1)△ABO~△DCO,因为∠1=∠2,∠AOB=∠DOC,所以△ABO~△DCO.
(2)△AOD~△BOC,由(1)知△ABO~△DCO,则.又因为∠AOD=∠BOC,所以△AOD~△BOC.
(3)△ACD~△BCE,由(2)知△AOD~△BOC,则∠DAO=∠CBO,又因为∠3=∠4,所以△ACD~△BCE.
(4)△ABC~△DEC,因为∠3=∠4,所以∠3+∠ECO=∠4+∠ECO,即∠BCA=∠ECD.又因为∠1=∠2,所以△ABC~△DEC.
11答案:解析:(1)∵△PCD是等边三角形,∴PC=CD=PD,∠PCD=∠PDC=60°,即∠PCA=∠PDB=120°,∴只要满足,就有△ACP~△PDB,∴关系式为或CD2=AC·BD.
(2)∵△ACP~△PDB,∴∠1=∠A,∠2=∠B.又∵∠PDC=∠1+∠B=60°,∴∠1+∠2=60°,∴∠APB=∠1+∠2+∠CPD=60°+60°=120°
12答案:解析:7对,分别是△ADG~△ABC,△BDE~△BAH,△ADI~△ABH,△ADI~△DBE,△AIG~△AHC,△AIG~△GFE,△GFC~△AHC.
13答案:解析:(1)当△ABC和△A′B′C′都是锐角三角形时,可得△ABC~△A′B′C′,如图①.
(2)当两个三角形都是直角三角形时,也可得△ABC~△A'B'C'.
(3)当两个三角形都是钝角三角形时,如图②,可得△ABC~△A'B'C'.
(4)当△ABC为锐角三角形,△A′B′C′为钝角三角形.虽然两个三角形有两边和其中一边上的高对应成比例,但两个三角形不相似.如图③.
14答案:△ADC~△EDO
△ADC~△EDO,△AOD~△FCD,△BEF~△OEA,△AFC~△EAO等等
15答案:解析:分两种情况,设经过x
s△PBQ与原△ABC相似.
(1)△BPQ~△BAC,则,即得t=2s;
(2)△BQP~△BAC,则,即得t=0.8s.
∴经过0.8s或2s时,△PBQ与原△ABC相似.
16答案:(1)0.6米
(2)1
884升
17答案:解析:∵PE⊥AB,∠C=90°,∴∠EPA=∠C=90°.又∵∠A为公共角,∴△AEP~△ABC,∴.又∵∠C=90°,AB=10,AC=8,可知BC=6.
∴,∴,,,
BP=10-x,∴,
∴.
设点E与点C重合,有CP⊥AB.又∠ACB=90°,∴CA2=AP·AB,即82=10AP,解之,得,故由P点与A点不重合,点E与点C不重合知x的取值范围是0∴y与x之间的关系式为:.
相似三角形的判定
基础能力训练
◆相似三角形的判定
1.已知菱形ABCD的边长是6,点E在直线AD上,DE=3,联结BE与对角线AC相交于点M,则的值是______.
2.如图19-5-4所示,E是平行四边形ABCD的一边BA延长线上的一点,CE交AD于点F,图中共有______对相似三角形,按对应顶点写出图中的相似三角形____________________.
3.如图19-5-5所示,已知△ABC中,AB=AC,∠A=36°,BD平分∠ABC,则BD=_______=_______.
4.如图19-5-6所示,∠l=∠2,若再增加一个条件就能使结论“AB·DE=AD·BC”成立,则这个条件可以是_______.
5.如图19-5-7所示,△ACD和△ABC具备下列哪个条件时,它们相似(
)
A.
B.
C.CB2=AD·BD
D.AC2=AD·AB
6.用—个放大镜看一个直角三角形,该直角三角形的边长放大到原来的5倍后,下列结论正确的是(
)
A.每个内角是原来的5倍
B.周长是原来的5倍
C.面积是原来的5倍
D.两条直角边的比值是原来的5倍
7.下列条件能判别△ABC~△DEF的是(
)
A.AB=4
cm,AC=3.2
cm,DE=2
cm,DF=1.6
cm,∠B=∠E=50°
B.AB=6
cm,BC=9
cm,AC=7.5
cm,DE=8
cm,EF=12
cm.DF=10
cm
C.∠A=∠D=70°,∠B=50°,∠E=60°
D.∠B=∠E=90°,
8.某班在布置新年联欢会会场时,需要将直角三角形彩纸裁成长度不等的矩形纸条,如图19-5-8所示,在Rt△ABC中,∠C=90°,AC=30
cm,AB=50
cm,依次裁下宽为1
cm的纸条a1、a2、a3、…,若使裁得的矩形纸条长度不小于5
cm,则每张直角三角形彩纸能裁成矩形纸条的条数为(
)
A.24
B.25
C.26
D.27
9.已知,如图19-5-9,Rt△∠ABC和Rt△A′B′C′中∠C=∠C′=90°,.△ABC与△A′B′C′是否相似,并说明理由.
10.如图19-5-10所示,四边形ABCD的对角线AC、BD相交于点O,∠1=∠2,∠3=∠4,指出图中哪些三角形相似,并说明理由.
11.如图19-5-11所示,点C、D在线段AB上,△PCD是等边三角形.(1)当AC、CD、DB满足怎样的关系时,△ACP~△PDB (2)当△ACP~△PDB时,求∠APB.
12.如图19-5-12所示,在△ABC中,AH是BC边上的高,四边形DEFG是△ABC的内接矩形,DG交AH于点I,则图中相似的三角形共有多少对 分别表示出来.
13.如果两个三角形中有两边和其中一边上的高对应成比例,则这两个三角形相似吗
综合创新训练
◆创新训练
14.已知:如图19-5-13,在平面直角坐标系中,矩形AOBC有两个顶点的坐标分别是A(0,6),C(8,6),x轴的正半轴上有一动点E(E与B不重合),作直线AE交对角线OC于D,或AE与BC相交于点F.
当点E在O、B间运动到某些位置时,作直线AE后,图中会出现相似不全等的三角形,请你把这个相似三角形写出来:_______;当E点运动到B点的右边时,请你写出此时图中三对相似而不全等的三角形:__________________.
15.如图19-5-14所示,在△ABC中,AB=8
am,BC=16
cm,点P从点A开始沿AB边向点B以2cm/s的速度移动,点Q从点B开始沿BC边向点C以4
cm/s的速度移动.如果P、Q分别从A、B同时出发,经过几秒钟△PBQ与原△ABC相似
16.一个圆柱形油桶,半径为1米,高为1.5米,用一根2米长的木棒从桶盖小口斜插桶内,另一端在小口处,抽出木棒后,量得上面没浸油的部分为1.2米,试求:
(1)油面的高度是多少
(2)桶内有油多少升 (1立方分米=1升,取3.14,取后结果精确到1升)
◆开放探索
17.如图19-5-15,在△ABC中,∠C=90°,P为AB上一点且点不与点A重合.过点P作PE⊥AB交AC边于E,点E不与点C重合.若AB=10,AC=8,设AP的长为x,四边形PECB的周长为y,试用x的代数式表示y.
参考答案
1答案:2或
解析:当点E在线段AD上时,如图(1),因为AB∥CD,所以△ABE~△DFE.所以,故DF=6.又因为△AMB~△CMF,所以.
当点E在线段AD的延长线上时,如图(2),容易得到△BCM~△EAM,
∴.
2答案:3
△EAF~△EBC,△EAF~△CDF,△EBC~△CDF
3答案:BC
AD
4答案:∠B=∠D,或∠C=∠AED,或AD:AB=AE:AC
解析:本题实质就是构造使△ADE与△ABC相似的条件.
5答案:D
解析:由AC2=AD·AB可得.又∠A=∠A,所以△ACD~△ABC.
6答案:B
7答案:B
解析:因为,三边对应成比例,所以两三角形相似.
8答案:C
解析:设第n条的长度恰好为5cm,且该矩形纸条与AC的交点为P点,与AB的交点为Q点,则PQ=5cm,设AP=x
cm,则△APQ~△ACB,得,即,解得:x=3.75,
∴CP=30-x=26.25.∵矩形宽为1
cm,取整数,可知矩形纸条为26条.
9答案:解析:相似,理由如下:∵,∴,两边平方,得,所以,由勾股定理得,因为,均为正数,则,即,而∠C=∠C′=90°,故Rt△ABC~Rt△A'B'C'.
10答案:解析:(1)△ABO~△DCO,因为∠1=∠2,∠AOB=∠DOC,所以△ABO~△DCO.
(2)△AOD~△BOC,由(1)知△ABO~△DCO,则.又因为∠AOD=∠BOC,所以△AOD~△BOC.
(3)△ACD~△BCE,由(2)知△AOD~△BOC,则∠DAO=∠CBO,又因为∠3=∠4,所以△ACD~△BCE.
(4)△ABC~△DEC,因为∠3=∠4,所以∠3+∠ECO=∠4+∠ECO,即∠BCA=∠ECD.又因为∠1=∠2,所以△ABC~△DEC.
11答案:解析:(1)∵△PCD是等边三角形,∴PC=CD=PD,∠PCD=∠PDC=60°,即∠PCA=∠PDB=120°,∴只要满足,就有△ACP~△PDB,∴关系式为或CD2=AC·BD.
(2)∵△ACP~△PDB,∴∠1=∠A,∠2=∠B.又∵∠PDC=∠1+∠B=60°,∴∠1+∠2=60°,∴∠APB=∠1+∠2+∠CPD=60°+60°=120°
12答案:解析:7对,分别是△ADG~△ABC,△BDE~△BAH,△ADI~△ABH,△ADI~△DBE,△AIG~△AHC,△AIG~△GFE,△GFC~△AHC.
13答案:解析:(1)当△ABC和△A′B′C′都是锐角三角形时,可得△ABC~△A′B′C′,如图①.
(2)当两个三角形都是直角三角形时,也可得△ABC~△A'B'C'.
(3)当两个三角形都是钝角三角形时,如图②,可得△ABC~△A'B'C'.
(4)当△ABC为锐角三角形,△A′B′C′为钝角三角形.虽然两个三角形有两边和其中一边上的高对应成比例,但两个三角形不相似.如图③.
14答案:△ADC~△EDO
△ADC~△EDO,△AOD~△FCD,△BEF~△OEA,△AFC~△EAO等等
15答案:解析:分两种情况,设经过x
s△PBQ与原△ABC相似.
(1)△BPQ~△BAC,则,即得t=2s;
(2)△BQP~△BAC,则,即得t=0.8s.
∴经过0.8s或2s时,△PBQ与原△ABC相似.
16答案:(1)0.6米
(2)1
884升
17答案:解析:∵PE⊥AB,∠C=90°,∴∠EPA=∠C=90°.又∵∠A为公共角,∴△AEP~△ABC,∴.又∵∠C=90°,AB=10,AC=8,可知BC=6.
∴,∴,,,
BP=10-x,∴,
∴.
设点E与点C重合,有CP⊥AB.又∠ACB=90°,∴CA2=AP·AB,即82=10AP,解之,得,故由P点与A点不重合,点E与点C不重合知x的取值范围是0
同课章节目录
- 第十八章 相似形
- 18.1 比例线段
- 18.2 黄金分割
- 18.3 平行线分三角形两边成比例
- 18.4 相似多边形
- 18.5 相似三角形的判定
- 18.6 相似三角形的性质
- 18.7 应用举例
- 第十九章 二次函数和反比例函数
- 19.1 二次函数
- 19.2 二次函数 y=ax2+bx+c(a≠0) 的图象
- 19.3 二次函数的性质
- 19.4 二次函数的应用
- 19.5 反比例函数
- 19.6 反比例函数的图象、性质和应用
- 第二十章 解直角三角形
- 20.1 锐角三角函数
- 20.2 30°、45°、60° 角的三角函数值
- 20.3 用科学计算器求锐角三角函数值
- 20.4 解直角三角形
- 20.5 测量与计算
- 第二十一章 圆(上)
- 21.1 圆的有关概念
- 21.2 过三点的圆
- 21.3 圆的对称性
- 21.4 圆周角
- 第二十二章 圆(下)
- 22.1 直线和圆的位置关系
- 22.2 圆的切线
- 22.3 正多边形的有关计算
