19.2 二次函数y=ax^2+bx+c(a≠0) 的图象 同步练习(含答案)
文档属性
| 名称 | 19.2 二次函数y=ax^2+bx+c(a≠0) 的图象 同步练习(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 129.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-11-07 15:13:28 | ||
图片预览



文档简介
19.2
二次函数y=ax2+bx+c(a≠0)的图象
基础能力训练
◆二次函数y=ax2+bx+c(a≠0)的图象
1.已知函数y=mxm2+m,当m=_____时,它的图象是开口向上的抛物线.
2.已知抛物线的图象经过点(a,4.5)和(-a,y1),则y1的值是_____.
3.函数的开口方向是______,对称轴是______,顶点坐标是_______.
4.抛物线y=x2-2x-3的对称轴是______,顶点坐标是______.
5.二次函数的图象由函数的图象先向_____平移_____个单位长度,再向_____平移_____个单位长度得到的.
6.二次函数y=ax2+bx+c中,a>0,b<0,c=0,则其图象的顶点应在第_____象限.
7.抛物线y=x2-2mx+m+2的顶点坐标在第三象限,则m的取值范围为_____.
8.已知二次函数y=x2-2x-3的图象与x轴交于A、B两点,在x轴上方,抛物线上有一点C,且△ABC的面积等于10,则C点的坐标为______.
9.已知二次函数y=ax2与一次函数y=3x-4的图象都经过(b,2),则a=_____,b=_____;试写出一个经过(a,b)点的抛物线的表达式_______.
10.函数y=ax2+bx+c的图象与y=2x2-3x-1的图象形状、大小相同,开口方向相反,则下面结论正确的是(
)
A.a=2,6=3,c=1
B.a=-2,b、c为任意实数
C.b=3,a、c为任意实数
D.c=1,a、b为不等于0的实数
11.二次函数y=kx2-6x+3的图象与x轴有交点,则k的取值范围是(
)
A.k>3
B.k>3且k≠0
C.k≤3
D.k≤3且k≠0
12.已知y=ax2+bx+c的图象如图20-2-4所示,则a、b、c的值满足(
)
A.a<0,b>0,c>0
B.a<0,b>0,c<0
C.a<0,b<0,c>0
D.a<0,b<0,c<0
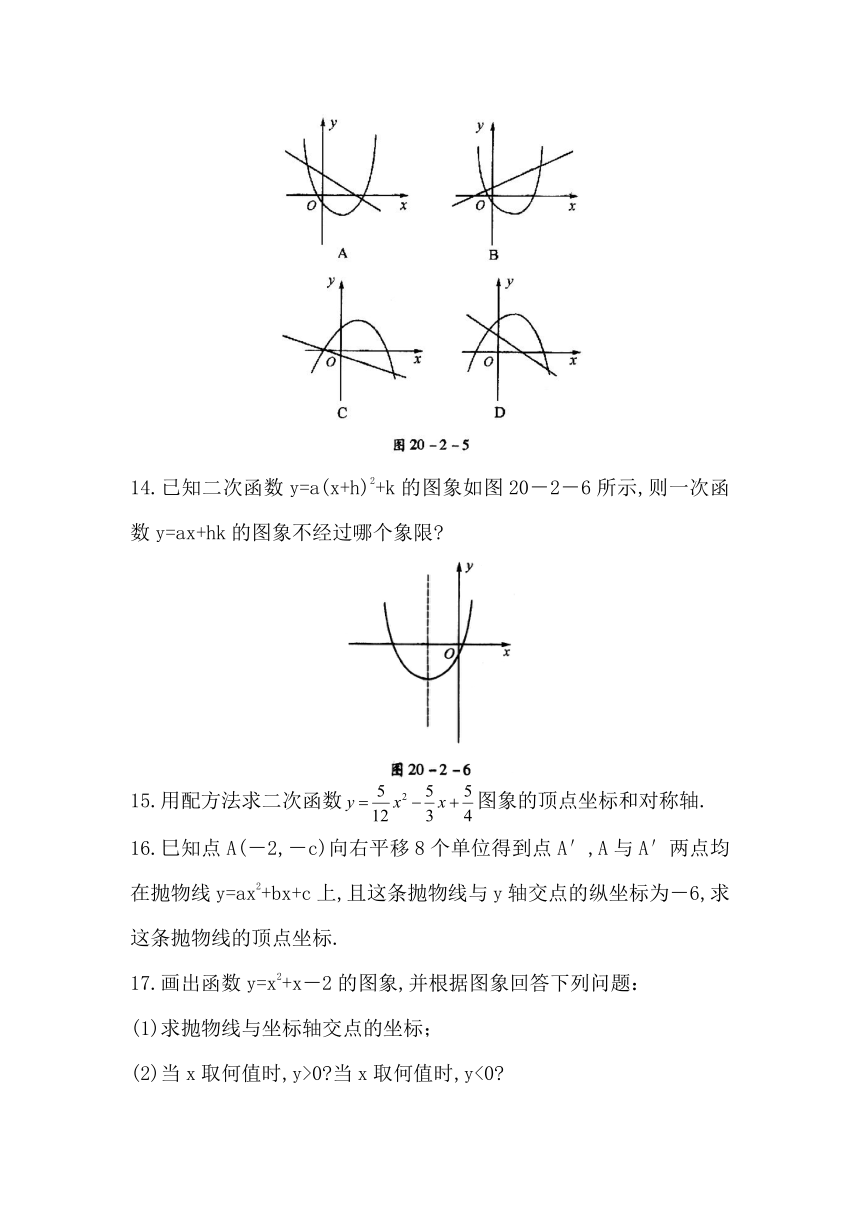
13.如图20-2-5,一次函数y=ax+b与二次函数y=ax2+bx+c在同一坐标系中的图象大致是(
)
14.已知二次函数y=a(x+h)2+k的图象如图20-2-6所示,则一次函数y=ax+hk的图象不经过哪个象限
15.用配方法求二次函数图象的顶点坐标和对称轴.
16.巳知点A(-2,-c)向右平移8个单位得到点A′,A与A′两点均在抛物线y=ax2+bx+c上,且这条抛物线与y轴交点的纵坐标为-6,求这条抛物线的顶点坐标.
17.画出函数y=x2+x-2的图象,并根据图象回答下列问题:
(1)求抛物线与坐标轴交点的坐标;
(2)当x取何值时,y>0 当x取何值时,y<0
(3)当x取何值时,y随x的增大而增大 x取何值时,y随x的增大而减小
(4)求抛物线y=x2+x-2的对称轴;
(5)该函数有最大值还是有最小值 x取何值时,y有最大值(或最小值) 最大值(或最小值)是多少
综合创新训练
◆创新应用
18.某市场经营一批进价为2元一件的商品,在市场调查中发现此商品的销售单价x(元)与日销售量y(件)之间有如下关系:
销售单价x(元)
3
5
9
11
销售量y(件)
18
14
6
2
(1)在所给的直角坐标系(如图20-2-7)中:①根据表中提供的数据描出实数对(x,y)的对应点;②猜测并确定日销售量y(件)与日销售单价x(元)之间的函数关系式,画出图象.
(2)设经营此商品的日销售利润(不考虑其他因素)为P元,根据日销售量规律:①试求出日销售利润P元与日销售单价x元之间的函数关系式,并求出日销售利润的最大值,试问日销售利润P是否存在最小值 若有,请求出;若无,请说明理由.②在给定的直角坐标系中,画出日销售利润P元与日销售单价x元之间的函数图象简图,观察图象,写出x、P的取值范围.
◆开放探索
19.阅读材料,解答问题.
阅读材料:
当抛物线的函数关系式中含有字母系数时,随着系数中的字母的取值不同,抛物线的顶点坐标也将发生变化.
例如:由抛物线y=x2-2mx+m2+2x-1,
①
有y=(x-m)2+2m-1,
②
∴抛物线的顶点坐标为(m,2m-1).
即
当m的值变化时,x、y的值也随之变化,因而y的值随x值的变化而变化,将③代人④得,y=2x-1.
⑤
可见,不论m取任何实数,抛物线的顶点的纵坐标y与横坐标x都满足关系式:y=2x-1.
解答问题:
(1)在上述过程中,由①到②所用的数学方法是_______,其中运用了_______公式,由③④得到⑤所用的数学方法是______.
(2)根据阅读材料提供的方法,确定抛物线y=x2-2mx+2m2-3m+1顶点的纵坐标y与横坐标x之间的关系式.
参考答案
1答案:1
解析:由题意知,该函数为二次函数,所以m2+m=2,解得m1=-2,m2=1,又因为图象开口向上,所以m=-2舍去,只取m=1.
2答案:4.5
解析:由题意知,a2=9,a=±3,将(-a,y1)代入,进一步求得y1=4.5.
3答案:向下
x=-3
(-3,6)
4答案:x=1
(1,-4)
解析:利用配方法可以得到结论,也可直接用对称轴和顶点坐标公式来求出结果.
5答案:左
3
下
2
解析:由及可知平移情况.
6答案:四
解析:由,可知抛物线的顶点必须在第四象限.
7答案:m<-1
解析:易得顶点坐标为(m,-m2+m+2).
∵顶点在第三象限,∴
解不等式组得:m<-1.
8答案:(4,5)或(-2,5)
解析:因为二次函数与x轴相交,所以令x2-2x-3=0,解得x1=-1,x2=3,所以AB之间的距离为4,S△ABC=×4×h=10,得h=5,即点C的纵坐标为5,所以有5=x2-2x-3,解得:x1=-2,x2=4,所以C点坐标为(4,5)或(-2,5).
9答案:
2
y=8x2(答案不唯一)
解析:直接代入,先求b,再进一步求a,符合条件的表达式可以由y=8x2,等(答案不唯一).
10答案:B
11答案:D
解析:由题意知:即
解得k≤3且k≠0.
注意:这里与x轴也可能只有一个交点,因此勿忘b2-4ac=0的情况.
12答案:A
解析:因为图象开口向下,所以a<0.又因为抛物线与y轴的交点在正半轴上,所以c>0.又因为,所以b>0,故选A
13答案:D
14答案:解析:由二次函数y=a(x+h)2+k的图象可知,因为抛物线的开口向上,所以a>0,因为抛物线的对称轴在y轴的左侧,所以h>0,又因为抛物线与y轴的交点在x轴下方,所以k<0,所以hk<0,由此可知,直线y=ax+hk经过第一、三、四象限,则一次函数y=ax+hk的图象不经过第二象限.
15答案:解析:,
∴该函数图象的顶点坐标是(2,),对称轴是x=2.
16答案:解析:抛物线的解析式是y=x2-4x-6,顶点坐标为(2,-10).
17答案:解析:(1)与x轴交点坐标是(-2,0)和(1,0),与y轴交点的坐标是(0,-2).
(2)当x<-2或x>1时,y>0,-2(3)当x>时,y随x的增大而增大,当x<时,y随x的增大而减小.
(4)对称轴为直线.
(5)有最小值,当时,.
18答案:解析:(1)①如图所示.
②函数关系式为y=-2x+24(0≤x≤12),函数图象如图a所示.
(2)①因为销售利润=售价-进货价,所以P=xy-2y.又因为y=-2x+24,所以P=y(x-2)=(-2x+24)(x-2)=-2(x-7)2+50.所以当x=7时,P最大=50,又当x>12时,即销售单价大于12元时,此时无人购买,所以此时利润为P=0(x≥12),由实际意义知,当销售单价x=0时,此时利润P=-48,即为最小值.
②根据实际意义,当0≤x<2时,亏本卖出;当x=-2或x=12时利润P=0;当x>12时,即高价卖,无人购买,此时利润P=0,如图b,由图象可知x≥0,-48≤P≤50.
19答案:解析:(1)配方法
完全平方
代入法
(2)由,,把x=m代入y=m2-3m+1得y=x2-3x+1,即为抛物钱y=x2-2mx+2m2-3m+1的顶点纵坐标y与横坐标x之间的关系式.
二次函数y=ax2+bx+c(a≠0)的图象
基础能力训练
◆二次函数y=ax2+bx+c(a≠0)的图象
1.已知函数y=mxm2+m,当m=_____时,它的图象是开口向上的抛物线.
2.已知抛物线的图象经过点(a,4.5)和(-a,y1),则y1的值是_____.
3.函数的开口方向是______,对称轴是______,顶点坐标是_______.
4.抛物线y=x2-2x-3的对称轴是______,顶点坐标是______.
5.二次函数的图象由函数的图象先向_____平移_____个单位长度,再向_____平移_____个单位长度得到的.
6.二次函数y=ax2+bx+c中,a>0,b<0,c=0,则其图象的顶点应在第_____象限.
7.抛物线y=x2-2mx+m+2的顶点坐标在第三象限,则m的取值范围为_____.
8.已知二次函数y=x2-2x-3的图象与x轴交于A、B两点,在x轴上方,抛物线上有一点C,且△ABC的面积等于10,则C点的坐标为______.
9.已知二次函数y=ax2与一次函数y=3x-4的图象都经过(b,2),则a=_____,b=_____;试写出一个经过(a,b)点的抛物线的表达式_______.
10.函数y=ax2+bx+c的图象与y=2x2-3x-1的图象形状、大小相同,开口方向相反,则下面结论正确的是(
)
A.a=2,6=3,c=1
B.a=-2,b、c为任意实数
C.b=3,a、c为任意实数
D.c=1,a、b为不等于0的实数
11.二次函数y=kx2-6x+3的图象与x轴有交点,则k的取值范围是(
)
A.k>3
B.k>3且k≠0
C.k≤3
D.k≤3且k≠0
12.已知y=ax2+bx+c的图象如图20-2-4所示,则a、b、c的值满足(
)
A.a<0,b>0,c>0
B.a<0,b>0,c<0
C.a<0,b<0,c>0
D.a<0,b<0,c<0
13.如图20-2-5,一次函数y=ax+b与二次函数y=ax2+bx+c在同一坐标系中的图象大致是(
)
14.已知二次函数y=a(x+h)2+k的图象如图20-2-6所示,则一次函数y=ax+hk的图象不经过哪个象限
15.用配方法求二次函数图象的顶点坐标和对称轴.
16.巳知点A(-2,-c)向右平移8个单位得到点A′,A与A′两点均在抛物线y=ax2+bx+c上,且这条抛物线与y轴交点的纵坐标为-6,求这条抛物线的顶点坐标.
17.画出函数y=x2+x-2的图象,并根据图象回答下列问题:
(1)求抛物线与坐标轴交点的坐标;
(2)当x取何值时,y>0 当x取何值时,y<0
(3)当x取何值时,y随x的增大而增大 x取何值时,y随x的增大而减小
(4)求抛物线y=x2+x-2的对称轴;
(5)该函数有最大值还是有最小值 x取何值时,y有最大值(或最小值) 最大值(或最小值)是多少
综合创新训练
◆创新应用
18.某市场经营一批进价为2元一件的商品,在市场调查中发现此商品的销售单价x(元)与日销售量y(件)之间有如下关系:
销售单价x(元)
3
5
9
11
销售量y(件)
18
14
6
2
(1)在所给的直角坐标系(如图20-2-7)中:①根据表中提供的数据描出实数对(x,y)的对应点;②猜测并确定日销售量y(件)与日销售单价x(元)之间的函数关系式,画出图象.
(2)设经营此商品的日销售利润(不考虑其他因素)为P元,根据日销售量规律:①试求出日销售利润P元与日销售单价x元之间的函数关系式,并求出日销售利润的最大值,试问日销售利润P是否存在最小值 若有,请求出;若无,请说明理由.②在给定的直角坐标系中,画出日销售利润P元与日销售单价x元之间的函数图象简图,观察图象,写出x、P的取值范围.
◆开放探索
19.阅读材料,解答问题.
阅读材料:
当抛物线的函数关系式中含有字母系数时,随着系数中的字母的取值不同,抛物线的顶点坐标也将发生变化.
例如:由抛物线y=x2-2mx+m2+2x-1,
①
有y=(x-m)2+2m-1,
②
∴抛物线的顶点坐标为(m,2m-1).
即
当m的值变化时,x、y的值也随之变化,因而y的值随x值的变化而变化,将③代人④得,y=2x-1.
⑤
可见,不论m取任何实数,抛物线的顶点的纵坐标y与横坐标x都满足关系式:y=2x-1.
解答问题:
(1)在上述过程中,由①到②所用的数学方法是_______,其中运用了_______公式,由③④得到⑤所用的数学方法是______.
(2)根据阅读材料提供的方法,确定抛物线y=x2-2mx+2m2-3m+1顶点的纵坐标y与横坐标x之间的关系式.
参考答案
1答案:1
解析:由题意知,该函数为二次函数,所以m2+m=2,解得m1=-2,m2=1,又因为图象开口向上,所以m=-2舍去,只取m=1.
2答案:4.5
解析:由题意知,a2=9,a=±3,将(-a,y1)代入,进一步求得y1=4.5.
3答案:向下
x=-3
(-3,6)
4答案:x=1
(1,-4)
解析:利用配方法可以得到结论,也可直接用对称轴和顶点坐标公式来求出结果.
5答案:左
3
下
2
解析:由及可知平移情况.
6答案:四
解析:由,可知抛物线的顶点必须在第四象限.
7答案:m<-1
解析:易得顶点坐标为(m,-m2+m+2).
∵顶点在第三象限,∴
解不等式组得:m<-1.
8答案:(4,5)或(-2,5)
解析:因为二次函数与x轴相交,所以令x2-2x-3=0,解得x1=-1,x2=3,所以AB之间的距离为4,S△ABC=×4×h=10,得h=5,即点C的纵坐标为5,所以有5=x2-2x-3,解得:x1=-2,x2=4,所以C点坐标为(4,5)或(-2,5).
9答案:
2
y=8x2(答案不唯一)
解析:直接代入,先求b,再进一步求a,符合条件的表达式可以由y=8x2,等(答案不唯一).
10答案:B
11答案:D
解析:由题意知:即
解得k≤3且k≠0.
注意:这里与x轴也可能只有一个交点,因此勿忘b2-4ac=0的情况.
12答案:A
解析:因为图象开口向下,所以a<0.又因为抛物线与y轴的交点在正半轴上,所以c>0.又因为,所以b>0,故选A
13答案:D
14答案:解析:由二次函数y=a(x+h)2+k的图象可知,因为抛物线的开口向上,所以a>0,因为抛物线的对称轴在y轴的左侧,所以h>0,又因为抛物线与y轴的交点在x轴下方,所以k<0,所以hk<0,由此可知,直线y=ax+hk经过第一、三、四象限,则一次函数y=ax+hk的图象不经过第二象限.
15答案:解析:,
∴该函数图象的顶点坐标是(2,),对称轴是x=2.
16答案:解析:抛物线的解析式是y=x2-4x-6,顶点坐标为(2,-10).
17答案:解析:(1)与x轴交点坐标是(-2,0)和(1,0),与y轴交点的坐标是(0,-2).
(2)当x<-2或x>1时,y>0,-2
(4)对称轴为直线.
(5)有最小值,当时,.
18答案:解析:(1)①如图所示.
②函数关系式为y=-2x+24(0≤x≤12),函数图象如图a所示.
(2)①因为销售利润=售价-进货价,所以P=xy-2y.又因为y=-2x+24,所以P=y(x-2)=(-2x+24)(x-2)=-2(x-7)2+50.所以当x=7时,P最大=50,又当x>12时,即销售单价大于12元时,此时无人购买,所以此时利润为P=0(x≥12),由实际意义知,当销售单价x=0时,此时利润P=-48,即为最小值.
②根据实际意义,当0≤x<2时,亏本卖出;当x=-2或x=12时利润P=0;当x>12时,即高价卖,无人购买,此时利润P=0,如图b,由图象可知x≥0,-48≤P≤50.
19答案:解析:(1)配方法
完全平方
代入法
(2)由,,把x=m代入y=m2-3m+1得y=x2-3x+1,即为抛物钱y=x2-2mx+2m2-3m+1的顶点纵坐标y与横坐标x之间的关系式.
同课章节目录
- 第十八章 相似形
- 18.1 比例线段
- 18.2 黄金分割
- 18.3 平行线分三角形两边成比例
- 18.4 相似多边形
- 18.5 相似三角形的判定
- 18.6 相似三角形的性质
- 18.7 应用举例
- 第十九章 二次函数和反比例函数
- 19.1 二次函数
- 19.2 二次函数 y=ax2+bx+c(a≠0) 的图象
- 19.3 二次函数的性质
- 19.4 二次函数的应用
- 19.5 反比例函数
- 19.6 反比例函数的图象、性质和应用
- 第二十章 解直角三角形
- 20.1 锐角三角函数
- 20.2 30°、45°、60° 角的三角函数值
- 20.3 用科学计算器求锐角三角函数值
- 20.4 解直角三角形
- 20.5 测量与计算
- 第二十一章 圆(上)
- 21.1 圆的有关概念
- 21.2 过三点的圆
- 21.3 圆的对称性
- 21.4 圆周角
- 第二十二章 圆(下)
- 22.1 直线和圆的位置关系
- 22.2 圆的切线
- 22.3 正多边形的有关计算
