19.6 反比例函数的图象、性质和应用 同步练习(含答案)
文档属性
| 名称 | 19.6 反比例函数的图象、性质和应用 同步练习(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 254.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-11-07 15:20:50 | ||
图片预览


文档简介
19.6
反比例函数的图象、性质和应用
基础能力训练
◆反比例函数的图象与性质
1.双曲线经过点(-2,-3),则k的值为_______.
2.若反比例函数y=(m-3)xm2-6m+7的图象在第一、三象限,那么m=_____.
3.反比例函数(k≠0)的图象的两个分支分别位于第_____象限.
4.已知y=(2m-2)xm2-5,当m=_____时,为反比例函数,且在每个象限内,y随x的增大而增大.
5.点A(a,b)、B(a-1,c)均在函数的图象上,若a<0,则b____c(填“>”“<”或“=”).
6.在双曲线上有一点P(m,n),PA⊥x轴于A,PB⊥y轴于B,原点为O,则矩形AOBP的面积为______.
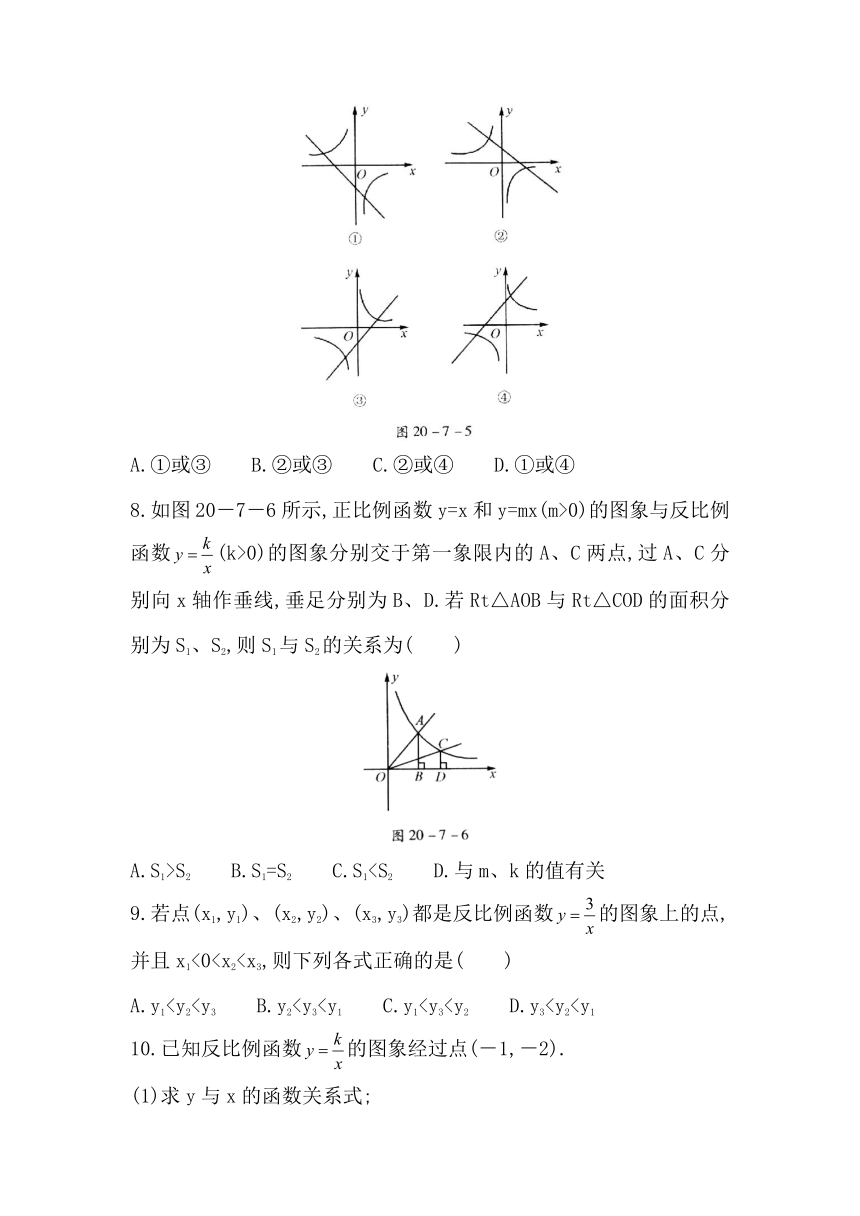
7.函数y=k(x-1)和(k≠0)在同一直角坐标系中的图象(如图20-7-5所示)大致是(
)
A.①或③
B.②或③
C.②或④
D.①或④
8.如图20-7-6所示,正比例函数y=x和y=mx(m>0)的图象与反比例函数(k>0)的图象分别交于第一象限内的A、C两点,过A、C分别向x轴作垂线,垂足分别为B、D.若Rt△AOB与Rt△COD的面积分别为S1、S2,则S1与S2的关系为(
)
A.S1>S2
B.S1=S2
C.S1D.与m、k的值有关
9.若点(x1,y1)、(x2,y2)、(x3,y3)都是反比例函数的图象上的点,并且x1<0)
A.y1B.y2C.y1D.y310.已知反比例函数的图象经过点(-1,-2).
(1)求y与x的函数关系式;
(2)若点(2,n)在这个图象上,求n的值.
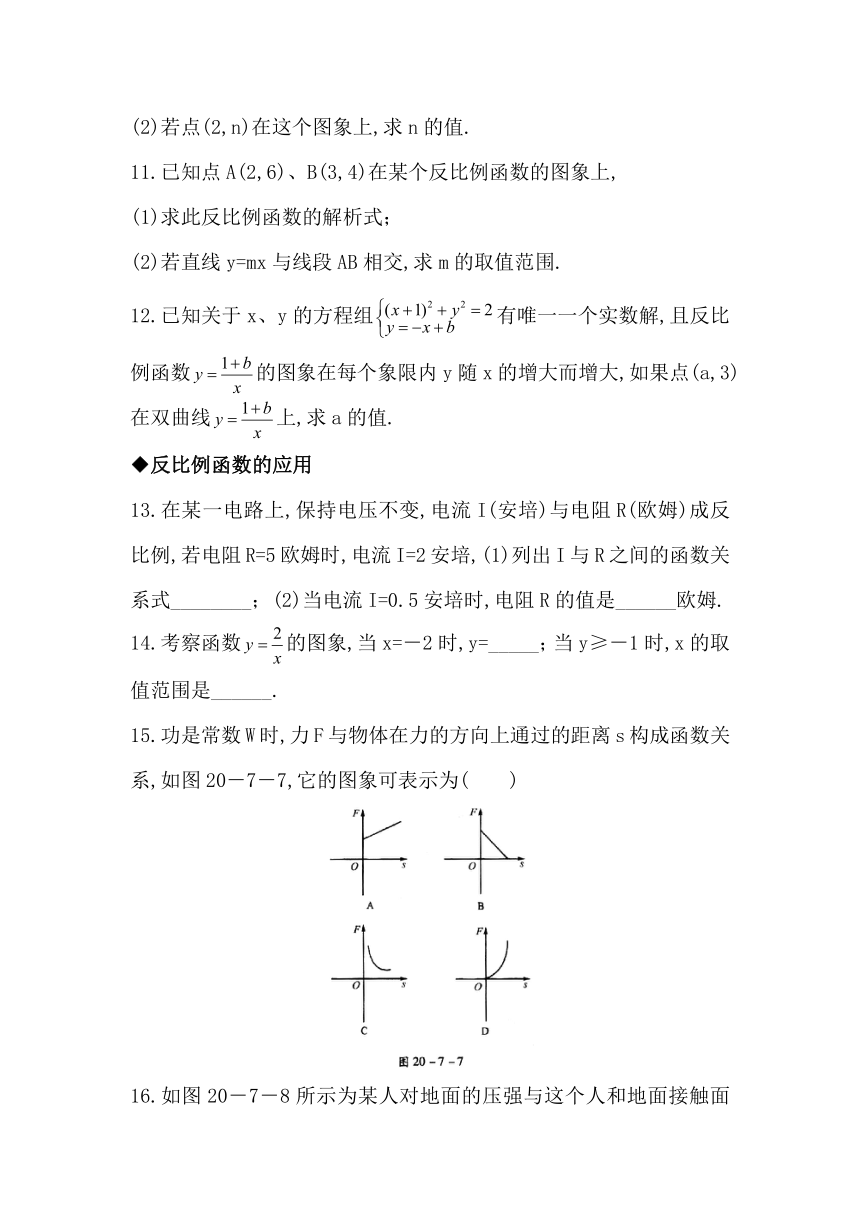
11.已知点A(2,6)、B(3,4)在某个反比例函数的图象上,
(1)求此反比例函数的解析式;
(2)若直线y=mx与线段AB相交,求m的取值范围.
12.已知关于x、y的方程组有唯一一个实数解,且反比例函数的图象在每个象限内y随x的增大而增大,如果点(a,3)在双曲线上,求a的值.
◆反比例函数的应用
13.在某一电路上,保持电压不变,电流I(安培)与电阻R(欧姆)成反比例,若电阻R=5欧姆时,电流I=2安培,(1)列出I与R之间的函数关系式________;(2)当电流I=0.5安培时,电阻R的值是______欧姆.
14.考察函数的图象,当x=-2时,y=_____;当y≥-1时,x的取值范围是______.
15.功是常数W时,力F与物体在力的方向上通过的距离s构成函数关系,如图20-7-7,它的图象可表示为(
)
16.如图20-7-8所示为某人对地面的压强与这个人和地面接触面积的函数关系图象.
(1)通过图象你能确定这个人的体重吗 (g取l0N/kg)
(2)如果此人穿40码的鞋,若每只鞋与地面的接触面积大约是300cm2,那么此人双脚站立时,对地面的压强有多大
(3)若某一沼泽地能承受的压强为300
N/m2,那么此人应站在面积至少多大的木板上才不至于下陷(木板的重量忽略不计)
17.某工厂的216名工人接受了生产1
000台AB型产品的任务,每台AB型产品由4个A型装置和3个B型装置配套而成,每个工人每小时可加工6个A型装置或3个B型装置.现将工人分成两组同时开始加工。每组分别加工一种装置,设加工A型装置有x人,如果加工以装置所用的时间为y1小时,加工B装置所用的时间为y2小时.
(1)分别写出用x表示y1和y2的函数关系式;
(2)比较y1和y2的大小;
(3)怎样分组,才能使完成任务的所用时间最短
综合创新训练
◆创新应用
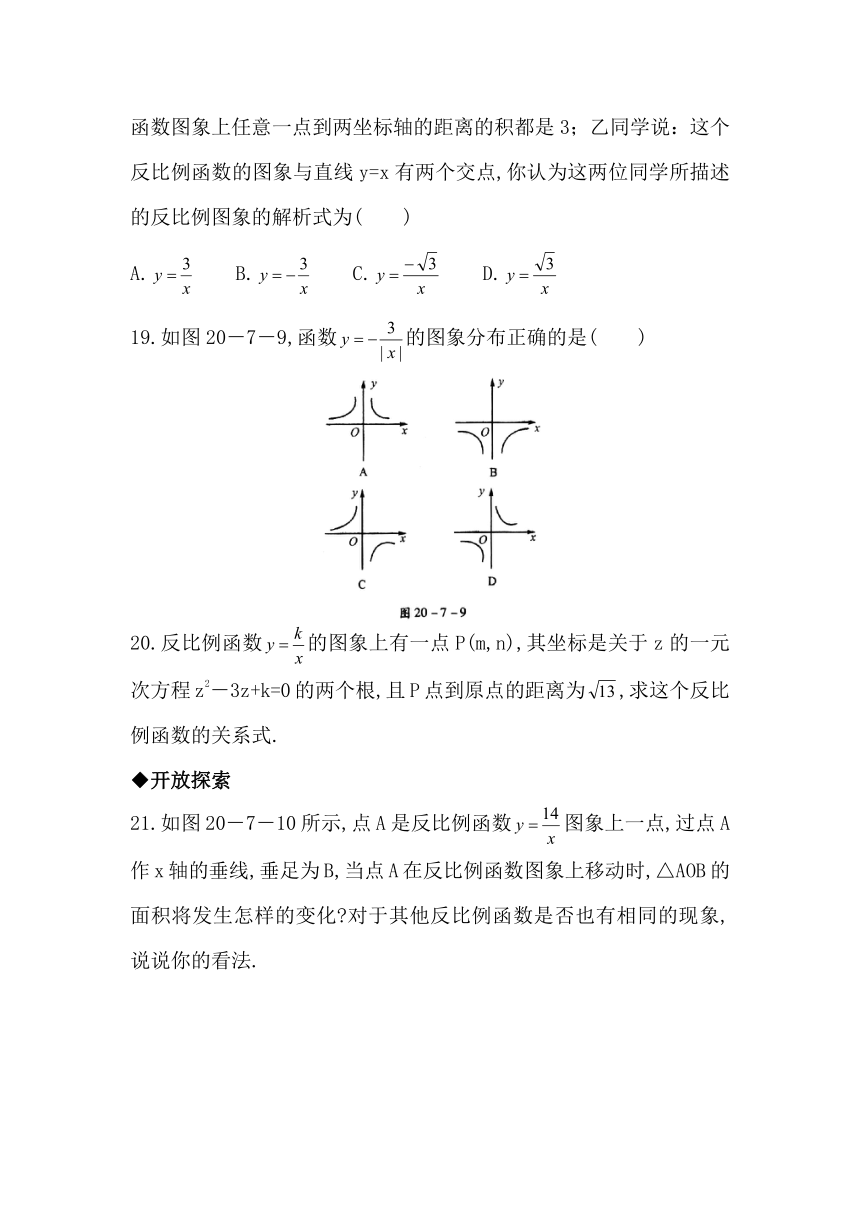
18.两位同学在描述同一反比例函数的图象时,甲同学说:这个反比例函数图象上任意一点到两坐标轴的距离的积都是3;乙同学说:这个反比例函数的图象与直线y=x有两个交点,你认为这两位同学所描述的反比例图象的解析式为(
)
A.
B.
C.
D.
19.如图20-7-9,函数的图象分布正确的是(
)
20.反比例函数的图象上有一点P(m,n),其坐标是关于z的一元次方程z2-3z+k=0的两个根,且P点到原点的距离为,求这个反比例函数的关系式.
◆开放探索
21.如图20-7-10所示,点A是反比例函数图象上一点,过点A作x轴的垂线,垂足为B,当点A在反比例函数图象上移动时,△AOB的面积将发生怎样的变化 对于其他反比例函数是否也有相同的现象,说说你的看法.
22.如图20-7-11,已知函数的图象和两条直线y=x、y=2x在第一象限内分别相交于Pl和P2两点,过P1分别作x轴,y轴的垂线P1Q1、P1R1,垂足分别为Q1、R1;过P2分别作x轴、y轴的垂线P2Q2、P2R2,垂足分别为Q2、R2.
(1)求矩形OQ1P1R1和OQ2P2R2的周长并比较它们的大小;
(2)求矩形OQ1P1R1和矩形OQ2P2R2的面积;
(3)由(2)你得到了什么结论
参考答案
1答案:6
2答案:4
解析:由题意知:m2-6m+7=-1,解得m1=2,m2=4,因为图象在一、三象限,所以m-3>0,得m>3,所以应取m=4.
3答案:一、三
解析:因为k≠0,所以无论k取任何实数时k2>0,所以图象必过一、三象限.
4答案:-2
解析:因为函数为反比例函数,所以,m2-5=-l,所以m=±2.又因在每个象限内y随x的增大而增大,所以2m-2<0,所以m<1,故取m=-2.
5答案:<
解析:∵a>a-1,且反比例函数的k=1>0,所以y随x的增大而减小,所以b6答案:6
解析:因为P(m,n)在图象上,所以代入得,∴mn=-6,∴|mn|=6,而矩形AOBP的面积为|mn|=6.
7答案:B
8答案:B
解析:设A(x1,y1)、C(x2,y2),因为A、C点在第一象限,所以x1>0,x2>0,y1>0,y2>0.把A、C两点代人(k>0)中,得x1y1=k,x2y2=k,
而,
,
∴S1=S2,故应选B.
9答案:C
解析:因为函数的图象分布在一、三象限,当x1<0时,y1<0;对于x3>x2>0,y随x的增大而减小,得y2>y3>0.综上可得y110答案:(1)
(2)
11答案:解析:(1)此反比例函数的解析式为.
(2)设P(x,y)是线段AB上任一点,则有2≤x≤3,4≤y≤6.因为,所以,即.
12答案:解析:将y=-x+b代入方程(x+1)2+y2=2得2x2+2(1-b)x+(b2-1)=0.因为方程组有唯一解,所以[2(1-b)]2-4×2(b2-1)=0,解这个方程得b1=1,b2=-3.
又因为的图象在每个象限内y随x的增大而增大,所以1+b<0,即b<-1,
所以取b=-3,所以1+b=-2,所以.
又点(a,3)在双曲线上,所以解得.
13答案:(1)
(2)20
14答案:-1
x≤-2或x>0
15答案:C
解析:由物理公式W=F·s得,根据实际意义它的图象可以归类为形如(k>0)的图象,这里x>0,因此只能为第一象限的图象,故选C.
16答案:解析:由图象可知,p与S满足反比例函数关系,设.
∵图象过点(10,60),∴,∴.
(1)∵F=600N,∴G=600=mg,∴m=60kg,
即这个人的体重为60kg.
(2)300cm2=0.03m2,S=0.03×2=0.06(m2)
当S=0.06时,(Pa)
∴此人双脚站立时对地面的压强为10
000
pa.
(3)∵p≤300,且,∴,解得S≥2,故此人应站立在面积至少2m2的木板上才不至于下陷.
17答案:解析:(1)加工A型装置有x人,则加工B型装置有(216-x)人,由题意,需加工A装置4000个,加工B装置3000个.
,(0(2),∵0∴216-x>0,当00,y1>y2;
当87≤x<216时,432-5x<0,y1(3)完成总时间的最小值,即是y1、y2中较大者的最小值.
当0当87≤x<216时,y2递增,∴x=87时,有最小值为,此时216-x=129.
故当加工A装置有86人,加工B装置有130人时,或加工A装置87人,加工B装置有129人时,完成任务时间最短,最短时间为小时,大约7小时45分钟.
18答案:A
解析:通过甲同学描述这一反比例函数图象的特点,得到|x|·|y|=3,即其解析式为或,排除C、D;通过乙同学描述这一反比例函数图象的特点,得到这一反比例函数的图象在第一、三象限,排除B,应选A.
19答案:B
解析:x的定义域为x≠0,无论x>0还是x<0,对应的y值均为负数,观察图象可知,只有B符合.
20答案:解析:因为点P(m,n)在反比例函数的图象上,所以,即mn=k,因为m、n为方程的根,所以m+n=3.
因为P点到原点的距离为,所以m2+n2=13.
因为
(m+n)2=m2+n2+2mn,所以9=13+2k,所以k=-2.
当k=-2时,一元二次方程z2-3z-2=0有两个根,所以反比例函数的关系式为.
21答案:解析:设点A(x,y),由已知可知A点的横纵坐标的绝对值,就是线段OB、BA的长,而,xy=14,.故△AOB的面积恒为7.同样对于任意反比例函数,有xy=k,.
22答案:解析:(1)设P1(x1,y1)、P2(x2,y2),
因为P1为y=x与在第一象限内的交点,所以由
得
矩形OQ1P1R1的周长=2×(2+2)=8.
同理可得矩形OQ2P2R2的周长=因为,所以矩形OQ2P2R2的周长大于矩形OQ1P1R1的周长.
(2)S矩形OQ1P1R1=x1·y1=2×2=4,
S矩形OQ2P2R2=x2·y2=
(3)从图象上任一点向两坐标轴作垂线段与坐标轴所构成的四边形的面积为定值4.
反比例函数的图象、性质和应用
基础能力训练
◆反比例函数的图象与性质
1.双曲线经过点(-2,-3),则k的值为_______.
2.若反比例函数y=(m-3)xm2-6m+7的图象在第一、三象限,那么m=_____.
3.反比例函数(k≠0)的图象的两个分支分别位于第_____象限.
4.已知y=(2m-2)xm2-5,当m=_____时,为反比例函数,且在每个象限内,y随x的增大而增大.
5.点A(a,b)、B(a-1,c)均在函数的图象上,若a<0,则b____c(填“>”“<”或“=”).
6.在双曲线上有一点P(m,n),PA⊥x轴于A,PB⊥y轴于B,原点为O,则矩形AOBP的面积为______.
7.函数y=k(x-1)和(k≠0)在同一直角坐标系中的图象(如图20-7-5所示)大致是(
)
A.①或③
B.②或③
C.②或④
D.①或④
8.如图20-7-6所示,正比例函数y=x和y=mx(m>0)的图象与反比例函数(k>0)的图象分别交于第一象限内的A、C两点,过A、C分别向x轴作垂线,垂足分别为B、D.若Rt△AOB与Rt△COD的面积分别为S1、S2,则S1与S2的关系为(
)
A.S1>S2
B.S1=S2
C.S1
9.若点(x1,y1)、(x2,y2)、(x3,y3)都是反比例函数的图象上的点,并且x1<0
A.y1
(1)求y与x的函数关系式;
(2)若点(2,n)在这个图象上,求n的值.
11.已知点A(2,6)、B(3,4)在某个反比例函数的图象上,
(1)求此反比例函数的解析式;
(2)若直线y=mx与线段AB相交,求m的取值范围.
12.已知关于x、y的方程组有唯一一个实数解,且反比例函数的图象在每个象限内y随x的增大而增大,如果点(a,3)在双曲线上,求a的值.
◆反比例函数的应用
13.在某一电路上,保持电压不变,电流I(安培)与电阻R(欧姆)成反比例,若电阻R=5欧姆时,电流I=2安培,(1)列出I与R之间的函数关系式________;(2)当电流I=0.5安培时,电阻R的值是______欧姆.
14.考察函数的图象,当x=-2时,y=_____;当y≥-1时,x的取值范围是______.
15.功是常数W时,力F与物体在力的方向上通过的距离s构成函数关系,如图20-7-7,它的图象可表示为(
)
16.如图20-7-8所示为某人对地面的压强与这个人和地面接触面积的函数关系图象.
(1)通过图象你能确定这个人的体重吗 (g取l0N/kg)
(2)如果此人穿40码的鞋,若每只鞋与地面的接触面积大约是300cm2,那么此人双脚站立时,对地面的压强有多大
(3)若某一沼泽地能承受的压强为300
N/m2,那么此人应站在面积至少多大的木板上才不至于下陷(木板的重量忽略不计)
17.某工厂的216名工人接受了生产1
000台AB型产品的任务,每台AB型产品由4个A型装置和3个B型装置配套而成,每个工人每小时可加工6个A型装置或3个B型装置.现将工人分成两组同时开始加工。每组分别加工一种装置,设加工A型装置有x人,如果加工以装置所用的时间为y1小时,加工B装置所用的时间为y2小时.
(1)分别写出用x表示y1和y2的函数关系式;
(2)比较y1和y2的大小;
(3)怎样分组,才能使完成任务的所用时间最短
综合创新训练
◆创新应用
18.两位同学在描述同一反比例函数的图象时,甲同学说:这个反比例函数图象上任意一点到两坐标轴的距离的积都是3;乙同学说:这个反比例函数的图象与直线y=x有两个交点,你认为这两位同学所描述的反比例图象的解析式为(
)
A.
B.
C.
D.
19.如图20-7-9,函数的图象分布正确的是(
)
20.反比例函数的图象上有一点P(m,n),其坐标是关于z的一元次方程z2-3z+k=0的两个根,且P点到原点的距离为,求这个反比例函数的关系式.
◆开放探索
21.如图20-7-10所示,点A是反比例函数图象上一点,过点A作x轴的垂线,垂足为B,当点A在反比例函数图象上移动时,△AOB的面积将发生怎样的变化 对于其他反比例函数是否也有相同的现象,说说你的看法.
22.如图20-7-11,已知函数的图象和两条直线y=x、y=2x在第一象限内分别相交于Pl和P2两点,过P1分别作x轴,y轴的垂线P1Q1、P1R1,垂足分别为Q1、R1;过P2分别作x轴、y轴的垂线P2Q2、P2R2,垂足分别为Q2、R2.
(1)求矩形OQ1P1R1和OQ2P2R2的周长并比较它们的大小;
(2)求矩形OQ1P1R1和矩形OQ2P2R2的面积;
(3)由(2)你得到了什么结论
参考答案
1答案:6
2答案:4
解析:由题意知:m2-6m+7=-1,解得m1=2,m2=4,因为图象在一、三象限,所以m-3>0,得m>3,所以应取m=4.
3答案:一、三
解析:因为k≠0,所以无论k取任何实数时k2>0,所以图象必过一、三象限.
4答案:-2
解析:因为函数为反比例函数,所以,m2-5=-l,所以m=±2.又因在每个象限内y随x的增大而增大,所以2m-2<0,所以m<1,故取m=-2.
5答案:<
解析:∵a>a-1,且反比例函数的k=1>0,所以y随x的增大而减小,所以b
解析:因为P(m,n)在图象上,所以代入得,∴mn=-6,∴|mn|=6,而矩形AOBP的面积为|mn|=6.
7答案:B
8答案:B
解析:设A(x1,y1)、C(x2,y2),因为A、C点在第一象限,所以x1>0,x2>0,y1>0,y2>0.把A、C两点代人(k>0)中,得x1y1=k,x2y2=k,
而,
,
∴S1=S2,故应选B.
9答案:C
解析:因为函数的图象分布在一、三象限,当x1<0时,y1<0;对于x3>x2>0,y随x的增大而减小,得y2>y3>0.综上可得y1
(2)
11答案:解析:(1)此反比例函数的解析式为.
(2)设P(x,y)是线段AB上任一点,则有2≤x≤3,4≤y≤6.因为,所以,即.
12答案:解析:将y=-x+b代入方程(x+1)2+y2=2得2x2+2(1-b)x+(b2-1)=0.因为方程组有唯一解,所以[2(1-b)]2-4×2(b2-1)=0,解这个方程得b1=1,b2=-3.
又因为的图象在每个象限内y随x的增大而增大,所以1+b<0,即b<-1,
所以取b=-3,所以1+b=-2,所以.
又点(a,3)在双曲线上,所以解得.
13答案:(1)
(2)20
14答案:-1
x≤-2或x>0
15答案:C
解析:由物理公式W=F·s得,根据实际意义它的图象可以归类为形如(k>0)的图象,这里x>0,因此只能为第一象限的图象,故选C.
16答案:解析:由图象可知,p与S满足反比例函数关系,设.
∵图象过点(10,60),∴,∴.
(1)∵F=600N,∴G=600=mg,∴m=60kg,
即这个人的体重为60kg.
(2)300cm2=0.03m2,S=0.03×2=0.06(m2)
当S=0.06时,(Pa)
∴此人双脚站立时对地面的压强为10
000
pa.
(3)∵p≤300,且,∴,解得S≥2,故此人应站立在面积至少2m2的木板上才不至于下陷.
17答案:解析:(1)加工A型装置有x人,则加工B型装置有(216-x)人,由题意,需加工A装置4000个,加工B装置3000个.
,(0
当87≤x<216时,432-5x<0,y1
当0
故当加工A装置有86人,加工B装置有130人时,或加工A装置87人,加工B装置有129人时,完成任务时间最短,最短时间为小时,大约7小时45分钟.
18答案:A
解析:通过甲同学描述这一反比例函数图象的特点,得到|x|·|y|=3,即其解析式为或,排除C、D;通过乙同学描述这一反比例函数图象的特点,得到这一反比例函数的图象在第一、三象限,排除B,应选A.
19答案:B
解析:x的定义域为x≠0,无论x>0还是x<0,对应的y值均为负数,观察图象可知,只有B符合.
20答案:解析:因为点P(m,n)在反比例函数的图象上,所以,即mn=k,因为m、n为方程的根,所以m+n=3.
因为P点到原点的距离为,所以m2+n2=13.
因为
(m+n)2=m2+n2+2mn,所以9=13+2k,所以k=-2.
当k=-2时,一元二次方程z2-3z-2=0有两个根,所以反比例函数的关系式为.
21答案:解析:设点A(x,y),由已知可知A点的横纵坐标的绝对值,就是线段OB、BA的长,而,xy=14,.故△AOB的面积恒为7.同样对于任意反比例函数,有xy=k,.
22答案:解析:(1)设P1(x1,y1)、P2(x2,y2),
因为P1为y=x与在第一象限内的交点,所以由
得
矩形OQ1P1R1的周长=2×(2+2)=8.
同理可得矩形OQ2P2R2的周长=因为,所以矩形OQ2P2R2的周长大于矩形OQ1P1R1的周长.
(2)S矩形OQ1P1R1=x1·y1=2×2=4,
S矩形OQ2P2R2=x2·y2=
(3)从图象上任一点向两坐标轴作垂线段与坐标轴所构成的四边形的面积为定值4.
同课章节目录
- 第十八章 相似形
- 18.1 比例线段
- 18.2 黄金分割
- 18.3 平行线分三角形两边成比例
- 18.4 相似多边形
- 18.5 相似三角形的判定
- 18.6 相似三角形的性质
- 18.7 应用举例
- 第十九章 二次函数和反比例函数
- 19.1 二次函数
- 19.2 二次函数 y=ax2+bx+c(a≠0) 的图象
- 19.3 二次函数的性质
- 19.4 二次函数的应用
- 19.5 反比例函数
- 19.6 反比例函数的图象、性质和应用
- 第二十章 解直角三角形
- 20.1 锐角三角函数
- 20.2 30°、45°、60° 角的三角函数值
- 20.3 用科学计算器求锐角三角函数值
- 20.4 解直角三角形
- 20.5 测量与计算
- 第二十一章 圆(上)
- 21.1 圆的有关概念
- 21.2 过三点的圆
- 21.3 圆的对称性
- 21.4 圆周角
- 第二十二章 圆(下)
- 22.1 直线和圆的位置关系
- 22.2 圆的切线
- 22.3 正多边形的有关计算
