20.1 锐角三角函数 同步练习(含答案)
文档属性
| 名称 | 20.1 锐角三角函数 同步练习(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 201.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-11-07 16:10:19 | ||
图片预览


文档简介
20.1
锐角三角函数
基础能力训练
◆锐角三角函数定义
1.如图21-1-5所示,在Rt△ABC中,tanA=_______,tanB=______,tanA·tanB=_______.
2.Rt△ABC中,∠C=90°,AC=5,BC=12,则sinA=_______,cosA=______,tanA=______.
3.已知∠A+∠B=90°,且cosA=,则cosB的值为_____.
4.sin30°+sin45°=_____.
5.在△ABC中,∠C=90°,若3AC=BC,则cosB=_____.
6.在Rt△ABC中,∠ACB=90°,BC=80
cm,tanB=,则AB=______.
7.在Rt△ABC中,将各边都扩大3倍,锐角的正弦、余
弦、正切(
)
A.没有变化
B.都大3倍
C.都缩小3倍
D.不能确定
8.在Rt△ABC中,斜边AB是直角边BC的5倍,下列各式正确的是(
)
A.sinB=
B.cosB=
C.tanB=
D.tanA=
9.在△ABC中,∠C=90°,如果tanA=,那么sinB等于(
)
A.
B.
C.
D.
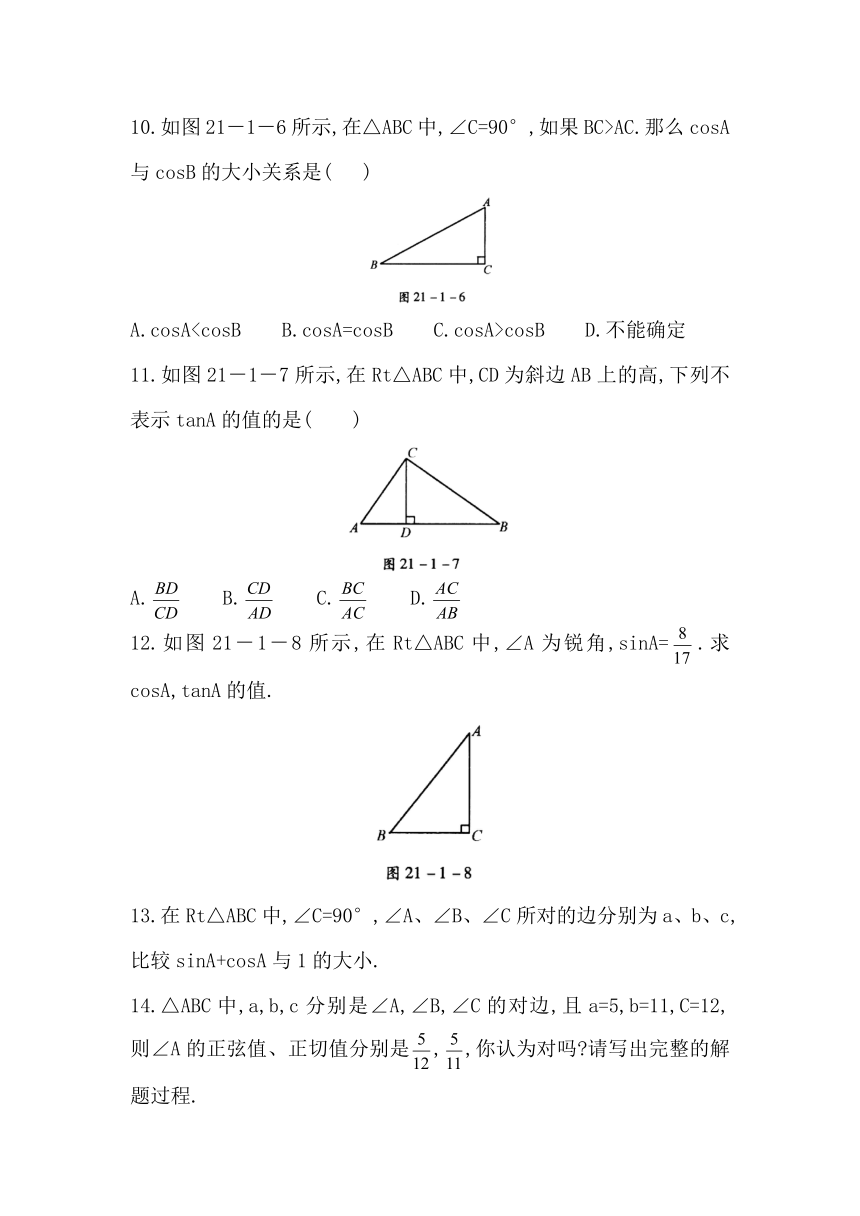
10.如图21-1-6所示,在△ABC中,∠C=90°,如果BC>AC.那么cosA与cosB的大小关系是(
)
A.cosAB.cosA=cosB
C.cosA>cosB
D.不能确定
11.如图21-1-7所示,在Rt△ABC中,CD为斜边AB上的高,下列不表示tanA的值的是(
)
A.
B.
C.
D.
12.如图21-1-8所示,在Rt△ABC中,∠A为锐角,sinA=.求cosA,tanA的值.
13.在Rt△ABC中,∠C=90°,∠A、∠B、∠C所对的边分别为a、b、c,比较sinA+cosA与1的大小.
14.△ABC中,a,b,c分别是∠A,∠B,∠C的对边,且a=5,b=11,C=12,则∠A的正弦值、正切值分别是,,你认为对吗 请写出完整的解题过程.
15.在Rt△ABC中,∠C=90°,如果tanA=,BC=10,求AC,AB的长及三角形面积.
16.如图21-1-9所示,在△ABC中,∠C=90°,D是AC边上的一点,且AD=DB=5,CD=3,求tan∠CBD和sinA.
综合创新训练
◆创新应用
17.青岛位于北纬36°30′,通过计算可以求得:在冬至日正午时的太阳入射角为30°30′.因此,在规划建设楼高为20米的小区时,两楼间的距离最小约为_____米,才能保证不挡光.(结果保留四个有效数字)(提示:sin30°30′=0.507
5,tan30°30′=0.5890)
18.交通宾馆在重新装修后,准备在大厅的主楼梯上铺设某种红色地毯,如果主楼梯的坡度(直角三角形中某一锐角的对边与邻边的比值,即为该角的正切值)为1:,且楼梯的竖直高度为3米,若所铺设的地毯每平方米售价为30元,主楼梯的宽度为2米,如图21-1-11所示,则购买地毯至少需要多少元钱
19.如图21-1-12(1),由直角三角形边角关系,可将三角形面积公式变形,得①,即三角形的面积等于两边之长与夹角正弦之积的一半,如图21-1-12(2)所示,在△ABC中,CD⊥AB于D,∠ACD=α,∠DCB=β,∵S△ABC=S△ADC+S△BDC②,你能利用直角三角形中的边角关系,消去②中的AC、BC、CD吗 如果不能,说明理由;如果能,写出解决过程.
参考答案
1答案:或
或
1
2答案:
解析:由勾股定理先求得AB=13,再根据三角函数的定义解答.
3答案:
解析:可把∠A、∠B放在如图所示的直角三角形中,由题意可设AC=k,则AB=5k,由勾股定理可得,所以.
4答案:
5答案:
解析:由条件不妨设,则BE=3k,故,于是.
6答案:100cm
解析:设AC=3a,由tanB=,故CB=4a=80cm,故a=20cm,从而AC=60
cm,故AB=100
cm.
7答案:A
8答案:B
9答案:B
10答案:A
解析:在△ABC中,∠C=90°,,,因为BC>AC,所以.即cosA11答案:D
12答案:解析:设BC=8k,则AB=17k,由勾股定理可得AC=15k.由定义可进一步求得,.
13答案:解析:由三角函数的定义可知:,,所以sinA+cosA,由三角形的三边关系定理可知,所以.
14答案:解析:不对,因为△ABC不是直角三角形,而三角函数是定义在直角三角形中的.
正确解法:
过点C作CD⊥AB,垂足为D.
设AD=x,则DB=12-x,在Rt△ADC中,CD2=AC2-AD2=112-x2;在Rt△CDB中,CD2=CB2-DB2=52-(12-x)2,所以112-x2=52-(12-x)2.
解得:x=10,所以.
所以.
15答案:AC=15,AB=,面积是75.
16答案:tan∠CBD=,sinA=
17答案:33.96
解析:该实际问题可转化为直角三角形的问题,即在直角△ABC中,∠C=90°,tan30°30′=,把AC=20,tan30°30′=0.589
0代入,进一步可求得BC≈33.96米.
18答案:解析:由题意知:,又BC=3米,
所以AB=米≈5.2米.
故AB+BC=3+5.2=8.2(米).
则购买地毯所需钱数至少为30×8.2×2=492(元).
19答案:解析:把AC·BC·sin(α+β)=AC·CD·sinα+BC·CD·sinβ,两边同除以AC·BC得:
sin(α+β)=,
∵,
∴.
锐角三角函数
基础能力训练
◆锐角三角函数定义
1.如图21-1-5所示,在Rt△ABC中,tanA=_______,tanB=______,tanA·tanB=_______.
2.Rt△ABC中,∠C=90°,AC=5,BC=12,则sinA=_______,cosA=______,tanA=______.
3.已知∠A+∠B=90°,且cosA=,则cosB的值为_____.
4.sin30°+sin45°=_____.
5.在△ABC中,∠C=90°,若3AC=BC,则cosB=_____.
6.在Rt△ABC中,∠ACB=90°,BC=80
cm,tanB=,则AB=______.
7.在Rt△ABC中,将各边都扩大3倍,锐角的正弦、余
弦、正切(
)
A.没有变化
B.都大3倍
C.都缩小3倍
D.不能确定
8.在Rt△ABC中,斜边AB是直角边BC的5倍,下列各式正确的是(
)
A.sinB=
B.cosB=
C.tanB=
D.tanA=
9.在△ABC中,∠C=90°,如果tanA=,那么sinB等于(
)
A.
B.
C.
D.
10.如图21-1-6所示,在△ABC中,∠C=90°,如果BC>AC.那么cosA与cosB的大小关系是(
)
A.cosA
C.cosA>cosB
D.不能确定
11.如图21-1-7所示,在Rt△ABC中,CD为斜边AB上的高,下列不表示tanA的值的是(
)
A.
B.
C.
D.
12.如图21-1-8所示,在Rt△ABC中,∠A为锐角,sinA=.求cosA,tanA的值.
13.在Rt△ABC中,∠C=90°,∠A、∠B、∠C所对的边分别为a、b、c,比较sinA+cosA与1的大小.
14.△ABC中,a,b,c分别是∠A,∠B,∠C的对边,且a=5,b=11,C=12,则∠A的正弦值、正切值分别是,,你认为对吗 请写出完整的解题过程.
15.在Rt△ABC中,∠C=90°,如果tanA=,BC=10,求AC,AB的长及三角形面积.
16.如图21-1-9所示,在△ABC中,∠C=90°,D是AC边上的一点,且AD=DB=5,CD=3,求tan∠CBD和sinA.
综合创新训练
◆创新应用
17.青岛位于北纬36°30′,通过计算可以求得:在冬至日正午时的太阳入射角为30°30′.因此,在规划建设楼高为20米的小区时,两楼间的距离最小约为_____米,才能保证不挡光.(结果保留四个有效数字)(提示:sin30°30′=0.507
5,tan30°30′=0.5890)
18.交通宾馆在重新装修后,准备在大厅的主楼梯上铺设某种红色地毯,如果主楼梯的坡度(直角三角形中某一锐角的对边与邻边的比值,即为该角的正切值)为1:,且楼梯的竖直高度为3米,若所铺设的地毯每平方米售价为30元,主楼梯的宽度为2米,如图21-1-11所示,则购买地毯至少需要多少元钱
19.如图21-1-12(1),由直角三角形边角关系,可将三角形面积公式变形,得①,即三角形的面积等于两边之长与夹角正弦之积的一半,如图21-1-12(2)所示,在△ABC中,CD⊥AB于D,∠ACD=α,∠DCB=β,∵S△ABC=S△ADC+S△BDC②,你能利用直角三角形中的边角关系,消去②中的AC、BC、CD吗 如果不能,说明理由;如果能,写出解决过程.
参考答案
1答案:或
或
1
2答案:
解析:由勾股定理先求得AB=13,再根据三角函数的定义解答.
3答案:
解析:可把∠A、∠B放在如图所示的直角三角形中,由题意可设AC=k,则AB=5k,由勾股定理可得,所以.
4答案:
5答案:
解析:由条件不妨设,则BE=3k,故,于是.
6答案:100cm
解析:设AC=3a,由tanB=,故CB=4a=80cm,故a=20cm,从而AC=60
cm,故AB=100
cm.
7答案:A
8答案:B
9答案:B
10答案:A
解析:在△ABC中,∠C=90°,,,因为BC>AC,所以.即cosA
12答案:解析:设BC=8k,则AB=17k,由勾股定理可得AC=15k.由定义可进一步求得,.
13答案:解析:由三角函数的定义可知:,,所以sinA+cosA,由三角形的三边关系定理可知,所以.
14答案:解析:不对,因为△ABC不是直角三角形,而三角函数是定义在直角三角形中的.
正确解法:
过点C作CD⊥AB,垂足为D.
设AD=x,则DB=12-x,在Rt△ADC中,CD2=AC2-AD2=112-x2;在Rt△CDB中,CD2=CB2-DB2=52-(12-x)2,所以112-x2=52-(12-x)2.
解得:x=10,所以.
所以.
15答案:AC=15,AB=,面积是75.
16答案:tan∠CBD=,sinA=
17答案:33.96
解析:该实际问题可转化为直角三角形的问题,即在直角△ABC中,∠C=90°,tan30°30′=,把AC=20,tan30°30′=0.589
0代入,进一步可求得BC≈33.96米.
18答案:解析:由题意知:,又BC=3米,
所以AB=米≈5.2米.
故AB+BC=3+5.2=8.2(米).
则购买地毯所需钱数至少为30×8.2×2=492(元).
19答案:解析:把AC·BC·sin(α+β)=AC·CD·sinα+BC·CD·sinβ,两边同除以AC·BC得:
sin(α+β)=,
∵,
∴.
同课章节目录
- 第十八章 相似形
- 18.1 比例线段
- 18.2 黄金分割
- 18.3 平行线分三角形两边成比例
- 18.4 相似多边形
- 18.5 相似三角形的判定
- 18.6 相似三角形的性质
- 18.7 应用举例
- 第十九章 二次函数和反比例函数
- 19.1 二次函数
- 19.2 二次函数 y=ax2+bx+c(a≠0) 的图象
- 19.3 二次函数的性质
- 19.4 二次函数的应用
- 19.5 反比例函数
- 19.6 反比例函数的图象、性质和应用
- 第二十章 解直角三角形
- 20.1 锐角三角函数
- 20.2 30°、45°、60° 角的三角函数值
- 20.3 用科学计算器求锐角三角函数值
- 20.4 解直角三角形
- 20.5 测量与计算
- 第二十一章 圆(上)
- 21.1 圆的有关概念
- 21.2 过三点的圆
- 21.3 圆的对称性
- 21.4 圆周角
- 第二十二章 圆(下)
- 22.1 直线和圆的位置关系
- 22.2 圆的切线
- 22.3 正多边形的有关计算
